加速器驱动次临界系统(Accelerator Driven Sub-critical System, ADS)^[1]由于强外源的引入和深次临界特性，在加速器束流瞬变时，外源发生快速变化，ADS在中子学上表现出较强的“时间-空间-能量”非均匀性，这给ADS中子动力学分析带来了新的挑战^[2]。

中子动力学研究通常采用的方法有时-空动力学和点堆动力学^[3-5]，准静态方法^[6-8]被广泛应用于时-空动力学。在点堆动力学和准静态方法的幅函数计算中均需要准确的中子学动态参数，它们由权重函数、动力学量算符和形状函数的卷积得到。传统的反应堆无需外源驱动即可实现自持运行，在点堆动力学的动态参数计算中，形状函数采用λ基波中子通量密度，权重函数采用共轭λ基波中子通量密度，它具有“临界堆中子价值”的物理含义；在准静态方法幅函数的动态参数计算中，形状函数一般由固定源问题输运（或扩散）方程的中子通量密度确定，权重函数同样采用共轭λ基波中子通量密度。

在ADS系统束流瞬变工况下，外源中子的快速变化使得次临界反应堆的中子通量密度分布、能谱等发生剧烈变化，中子动力学特性较为复杂，点堆动力学和准静态方法幅函数的动态参数计算采用何种形状函数和权重函数仍需要更深入的研究；同时，采用准静态方法进行ADS启堆分析时，由于初始时刻次临界反应堆中子通量密度为零，初始时刻动态参数计算所用的形状函数如何“假设”，同样需要进行研究。

基于改进的准静态方法(Improved Quasi-Static method, IQS)，本文分别采用不同的权重函数和初始形状函数模拟启堆过程和断束工况的动力学结果，并与直接求解时空动力学方程所得到的结果进行对比，从而选取适合启堆过程和断束工况的权重函数和形状函数。在此基础上，通过对权重函数物理意义的研究，深化对“次临界堆中子价值”的认识。

考虑缓发中子和外源中子的ADS时-空动力学方程可由方程组(1)表示：

式中：$\phi (r, E, t)$为中子通量密度；$-L\phi (r, E, t)$表示t时刻中子泄漏、移出和散射对位置r处能量为E的中子通量密度变化率的贡献；算子L在中子扩散方程中可表示为：

式中：$D(r, E)$为扩散系数；${\mathit{\Sigma }_t}(r, E)$为总宏观截面；${\mathit{\Sigma }_s}(r, E' \to E)$为宏观散射截面；$(1-\beta ){\chi _p}F\phi (r, E, t)$表示裂变产生的瞬发中子的贡献，其中β为缓发中子总份额，${\chi _p}$为瞬发中子能谱，算子F在中子扩散方程中可表示为：

假设中子通量密度$\phi (r, E, t)$可以被因式分解为形状函数$\varphi (r, E, t)$和幅函数$n(t)$的乘积：

将式(3)代入方程组(1)，经过一系列变换，可得到幅函数n(t)的方程：

其中：

描述幅函数的方程(4)也被称为精确点堆动力学方程，它直接由中子时-空动力学方程推导得到。可以采用Gear方法^[9]求解方程获取幅函数$n(t)$。

在IQS方法中，某一时刻t的形状函数可通过对时间的一阶差分方程(13)得到：

其中：$t'{\rm{ = }}t-\Delta t$，$\Delta t$为时间步长；${S_d} = \sum\limits_{i = 1}^n {{\chi _{d, i}}{\lambda _i}{C_i}(r, t)} $为缓发中子源项，${C_i}(r, t) = {C_i}(r, {t_0}) \cdot {{\rm{e}}^{-{\lambda _i}(t-{t_0})}} + \int_{{t_0}}^t {{{\rm{e}}^{-{\lambda _i}(t - t')}} \cdot {\beta _i}F\phi (r, E, t'){\rm{d}}t{\rm{'}}} $为缓发中子先驱核浓度。

对于权重函数的选取，数学上虽未对权重函数做特殊要求，但通常希望它既可以提高动态计算精度，又具备良好物理含义。物理上认为ADS准静态模型中应采用“次临界堆中子价值”作为权重函数，但其有效性仍需通过实践检验。本文在计算幅度函数的动态参数时，选用的权重函数模型^[9-10]主要分为：临界权重函数模型和全局稳态权重函数模型。

1) 临界权重函数模型

本文采用的临界权重函数模型又分为两种：共轭λ基波中子通量密度和共轭瞬发α基波中子通量密度，它们分别是方程(14)、(15)的解${\varphi ^ * }$。

式中：$\varphi _\lambda ^*$具有“临界反应堆中子价值”的物理含义，是传统点堆动力学模型动态参数计算最常用的权重函数；$\varphi _\alpha ^*$是瞬发α本征值问题的共轭解，瞬发α本征值是描述偏离临界的反应堆中子倍增特性的“天然本征值”。

2) 全局稳态权重函数模型

全局稳态权重函数模型实际上是ADS反应堆稳态中子平衡方程的共轭方程的解，本文采用存在于全堆范围内的裂变中子产生截面$\nu {\mathit{\Sigma }_f}$作为共轭源，如方程(16)所示。

裂变中子产生截面作为ADS反应堆的共轭源，它的物理意义可以表述为：在次临界系统中单位时间内一个外源中子在某一位置产生的响应，即外源中子对全堆稳定裂变功率的贡献。

在模拟ADS反应堆启堆过程的中子动力学时，由于初始时刻的中子通量密度为0，这导致IQS计算时，初始时刻形状函数$\varphi (r, E, t)$的选择具有一定的“任意性”。因此，本文在模拟ADS反应堆启堆过程时，除了考虑权重函数的影响之外，还选择了三种初始形状函数：λ基波中子通量密度、瞬发α基波中子通量密度和ADS反应堆稳态中子通量密度进行研究。断束工况下初始形状函数则通过断束时刻的稳态中子通量密度获取。

在启堆过程中，三种初始形状函数和三种权重函数两两组合，可以得到9种动态参数的计算模型，见表 1；在断束过程中，初始时刻的形状函数和幅函数通过基准值获取，因此仅需考虑三种权重函数的影响。

表 1

表 1 启堆过程动态参数计算模型 Table 1 Models for kinetic parameters calculation in starting progress 模型 Model 形状函数 The shape function 权重函数 The weighting function 简记形式 The abbreviated form 1 λ基波中子通量密度(λ) λ fundamental neutron flux 共轭λ基波中子通量密度(λ*) λ adjoint fundamental neutron flux λ-λ* 2 共轭瞬发α基波中子通量密度(α* Prompt α adjoint fundamental neutron flux λ-α* 3 ADS反应堆稳态共轭中子通量密度(s*) Steady adjoint neutron flux of ADS λ-s* 4 瞬发α基波中子通量密度(α) Prompt α fundamental neutron flux 共轭λ基波中子通量密度(λ*) λ adjoint fundamental neutron flux α-λ* 5 共轭瞬发α基波中子通量密度(α*) Prompt α adjoint fundamental neutron flux α-α* 6 ADS反应堆稳态共轭中子通量密度(s*) Steady adjoint neutron flux of ADS α-s* 7 ADS反应堆稳态中子通量密度(s) Steady neutron flux of ADS 共轭λ基波中子通量密度(λ*) λ adjoint fundamental neutron flux s-λ* 8 共轭瞬发α基波中子通量密度(α*) Prompt α adjoint fundamental neutron flux s-α* 9 ADS反应堆稳态共轭中子通量密度(s*) Steady adjoint neutron flux of ADS s-s*

表 1 启堆过程动态参数计算模型 Table 1 Models for kinetic parameters calculation in starting progress

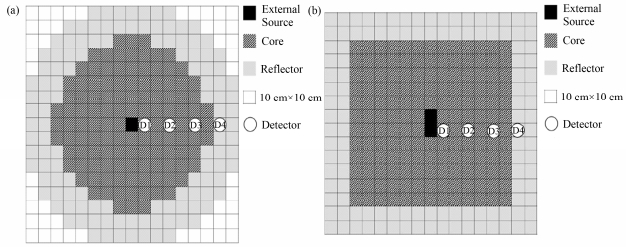
本文研究的ADS反应堆堆芯为三维圆柱体结构^[13-14]，本文将堆芯等效为方形燃料组件准圆形布置方式，如图 1所示。燃料和反射层为10 cm×10 cm的方形组件；堆芯中央位置有一外中子源，高度为20 cm，各向同性发射。为了研究不同次临界度下的中子动力学特性，通过调节堆芯裂变中子产生截面$\nu {\mathit{\Sigma }_{\rm{f}}}$，由扩散程序DONJON计算得到k_eff=0.99（浅次临界度）、k_eff=0.96（中等次临界度）、k_eff=0.93（深次临界度）三种次临界度。ADS反应堆的4群均匀化截面如表 2所示，堆内设置的稳态外中子源强度为1×10⁷ cm^-3∙s^-1，初始能量落在第1能群。

图 1

图 1 ADS反应堆堆芯布置示意图(a)水平剖面，(b)竖直剖面 Figure 1 Schematic diagram of ADS reactor (a) Horizontal profile, (b) Vertical profile

表 2

表 2 ADS堆芯和反射层组件均匀化参数 Table 2 The homogeneous parameters of core and reflector in ADS reactor 组件类型 The type of subassembly 均匀化参数 The homogeneous parameters 能群The group 1 2 3 4 堆芯组件 The subassembly of the core D / cm 2.2233 1.1491 6.9322×10-1 2.6386×10-1 ${\mathit{\Sigma }_t}$/ cm-1 7.1226×10-2 7.4597×10-2 8.6783×10-2 1.1085×10-2 $\nu {\mathit{\Sigma }_f}$/ cm-1 5.5726×10-3 a 1.3694×10-3 a 1.6613×10-2 a 1.2906×10-1 a 5.4037×10-3 b 1.3279×10-3 b 1.6110×10-2 b 1.2515×10-1 b 5.2349×10-3 c 1.2864×10-3 c 1.5606×10-2 c 1.2124×10-1 c ${\mathit{\Sigma }_{{\rm{g}} \to {\rm{g + }}1}}$/ cm-1 6.8312×10-2 7.2630×10-2 6.3705×10-2 0 ${\chi _d}, {\chi _p}$ 7.5560×10-1 2.4382×10-1 5.8000×10-4 0 v/cm·s-1 1.9600×109 4.6400×108 6.2300×106 4.2600×105 反射层组件 The subassembly of the reflector D / cm 1.1012 5.1096×10-1 2.7453×10-1 1.5160×10-1 ${\mathit{\Sigma }_t}$/ cm-1 1.1803×10-1 1.1650×10-1 1.2663×10-1 1.4449×10-1 ${\mathit{\Sigma }_{{\rm{g}} \to {\rm{g + }}1}}$/ cm-1 1.1664×10-1 1.1564×10-1 1.1187×10-1 0 v/cm·s-1 1.9600×109 4.6400×108 6.2300×106 4.2600×105 注：a) keff=0.99；b) keff=0.96；c) keff=0.93 Note: a) keff=0.99; b) keff =0.96; c) keff=0.93

表 2 ADS堆芯和反射层组件均匀化参数 Table 2 The homogeneous parameters of core and reflector in ADS reactor

本文将讨论不同次临界度、不同外源驱动模式下，不同的初始形状函数和权重函数对采用改进准静态方法计算的中子动力学结果（以下简称IQS中子动力学结果）的影响，并与时-空动力学方程直接求解程序的结果（基准值）进行对比，以此确定适合不同外源驱动模式的动态参数权重函数和初始形状函数。

需要说明的是，为了使IQS时-空动力学结果和基准值的对比更加简洁，本文所计算的中子动力学物理量为全堆中子数目。

本文研究两种外源驱动模式：1)启堆：在启堆过程中，次临界系统在稳态外源的驱动下，堆内中子通量密度从0逐步达到稳定水平；2)断束：在ADS系统内中子通量密度达到稳定水平后，切断外源中子，中子通量密度随时间衰减。

分别模拟5 min内启堆过程和断束过程的中子动力学结果，与基准值进行对比发现，不同准静态动力学结果与基准值之间的误差集中在外源发生变化后极短的时间内(< 0.1 s)，以下，我们将研究的时间范围缩小到0.05 s之内。

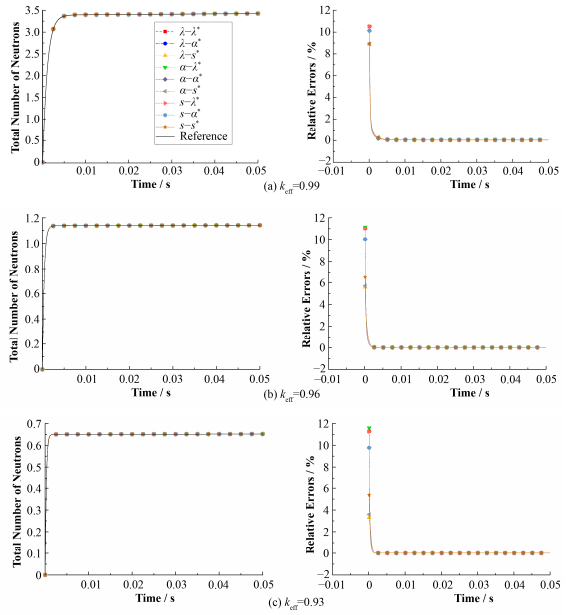
在ADS反应堆启堆过程中，加速器束流在零时刻瞬间启动，并达到额定强度，此时外中子源强度也达到额定强度。图 2(a)-(c)分别为k_eff=0.99、0.96和0.93情况下，采用不同权重函数和初始形状函数计算得到的全堆中子数目$N(t)$随时间的变化以及与基准值的相对误差，其中基准值来自时空动力学直接求解结果。

从图 2中可以看到，9组IQS中子动力学结果在启堆后的极短时间内（对于k_eff=0.99、0.96、0.93，这一时间长度分别约为0.005 s、0.003 s、小于0.003s）与基准值的相对误差均较大，最高可达11%左右；但随着时间的推移，相对误差急剧减小，然后趋于稳定。

图 2

图 2 不同次临界度下启堆过程中子动力学结果及相对误差 Figure 2 The kinetic results of the starting process in different sub-criticality and their relative errors

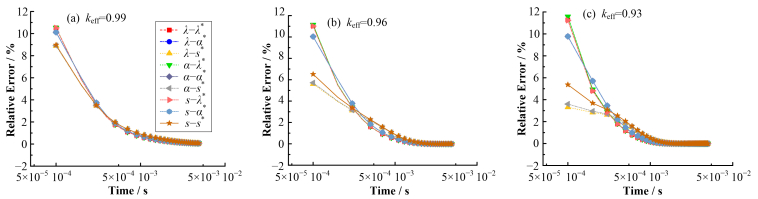
采用不同动态参数模型的动力学结果之间偏差主要集中在误差迅速减小的这段时间内。为了对这段时间内的相对误差进行细致的研究，将0~0.005 s时段的误差放置在对数坐标内，见图 3。其中，图 3(a)-(c)分别为k_eff=0.99、0.96和0.93情况下，0~0.005 s时段的相对误差。

图 3

图 3 不同次临界度下启堆过程中子动力学结果与基准值的相对误差（对数坐标） Figure 3 The relative errors between the kinetic results and the reference results in the starting process in different sub-criticality (logarithmic coordinate)

从相对误差曲线中可以发现，在同一次临界度下，权重函数对中子动力学结果的影响占主导地位。在初始时刻后的2~3个时间点上(0~0.0005 s)，采用ADS反应堆稳态共轭中子通量密度作为权重函数的三种模型——λ-s^*、α-s^*、s-s^*，模型结果与基准值的相对误差最小；在此后的时间内，采用共轭λ基波中子通量密度作为权重函数的三种模型——λ-λ^*、α-λ^*、s-λ^*，模型结果与基准值的相对误差变为最小，而λ-s^*、α-s^*、s-s^*模型的相对误差变为最大。随着次临界度的加深，不同中子动力学结果之间的偏差愈发明显：在初始时刻后的2~3个时间点上，λ-s^*、α-s^*、s-s^*模型结果误差随次临界的加深，从9%下降到6%，而其他6组结果的相对误差反而略有上升；在0.0005~0.005 s时段内，选用λ-λ^*、α-λ^*、s-λ^*模型的优势也愈发明显。

为了衡量整个启堆过程中9组IQS动力学结果的偏差大小，对各时间点计算值误差的绝对值求和，以此量化各模型的精确程度，见表 3。从表 3中可以看到，对于启堆过程，采用s-λ^*模型计算出的结果与基准值的总体偏差最小。

表 3

表 3 各组IQS中子动力学结果与基准值的偏差之和 Table 3 The sun of the deviations between the IQS results and the reference result 模型 Model 误差的绝对值之和 The sum of the absolute value of the errors keff=0.99 keff=0.96 keff=0.93 1 λ-λ* 1.03443 0.18541 0.09101 2 λ-α* 1.05735 0.19966 0.10118 3 λ-s* 1.12669 0.21846 0.09486 4 α-λ* 1.03492 0.18658 0.09273 5 α-α* 1.05735 0.19966 0.10118 6 α-s* 1.12725 0.21968 0.09662 7 s-λ* 1.03440 0.18529 0.09083 8 s-α* 1.05735 0.19966 0.10118 9 s-s* 1.12921 0.22815 0.10742

表 3 各组IQS中子动力学结果与基准值的偏差之和 Table 3 The sun of the deviations between the IQS results and the reference result

从结果中可以得出以下结论：对于启堆过程，初始形状函数对IQS中子动力学结果的影响是细微的，动力学结果之间的差异主要由权重函数引入；在不同次临界度下，采用共轭λ基波中子通量密度(λ^*)作为权重函数所获得的动力学结果与基准值符合得较好；其中采用ADS反应堆稳态中子通量密度作为初始形状函数、共轭λ基波中子通量密度作为权重函数(s-λ^*)能获得更为准确的中子动力学结果。

ADS反应堆在断束前处于稳态运行状态，在零时刻突然切断加速器束流，此时外中子源强度在瞬间由额定强度降为零。图 4(a)-(c)分别为k_eff=0.99、0.96和0.93情况下，采用不同权重函数和形状函数组成的动态参数模型计算得到的全堆中子数目$N(t)$随时间的变化以及与基准值的相对误差，其中基准值来自时空动力学直接求解结果。

图 4

图 4 不同次临界度下断束工况中子动力学结果及相对误差 Figure 4 The kinetic results of the beam loss condition in different sub-criticality and their relative errors

从图 4中可以看到，9组IQS中子动力学结果的相对误差呈现一种先减小再增大最后趋于稳定的趋势。在断束发生后的几个时间点，9组IQS中子动力学结果的相对误差均大于零，即在这几个时间点IQS中子动力学计算结果大于基准值；随着时间的推移，IQS中子动力学结果的相对误差降为负数；在达到相对误差的最小值时，IQS动力学结果的相对偏差达到最大；此后，相对误差的绝对值逐渐减小，逐渐稳定在稳定水平：在不同次临界度下，IQS动力学结果的稳定误差均维持在-0.5%左右。

采用不同动态参数模型的动力学结果之间偏差主要集中在误差迅速减小的这段时间内，对于k_eff=0.99、0.96和0.93这三种次临界度，这段时间的长度分别约为0.01 s、0.005 s、0.003 s。为了对这段时间内的相对误差进行细致的研究，将0~0.005 s时段的误差放置在对数坐标内，见图 5。其中，图 5(a)-(c)分别为k_eff=0.99、0.96和0.93情况下0~ 0.005s时段的相对误差。

图 5

图 5 不同次临界度下断束工况中子动力学结果与基准值的相对误差（对数坐标） Figure 5 The relative errors between the kinetic results and the reference results in beam loss condition in different sub-criticality (logarithmic coordinate)

通过观察不同次临界度下的相对误差曲线可以发现：采用ADS次临界反应堆稳态共轭中子通量密度作为权重函数的中子动力学结果，除了在初始时候后的第一个时间点的相对误差略高于其他两组结果外，在其他时刻的相对误差的绝对值均为最小；此外，采用共轭λ基波中子通量密度和共轭α基波中子通量密度作为权重函数的中子动力学结果之间，几乎不存在差异。

从结果中可以得出以下结论：在不同次临界度下，采用ADS反应堆稳态共轭中子通量密度(s^*)作为权重函数，能使IQS中子动力学结果更加准确。

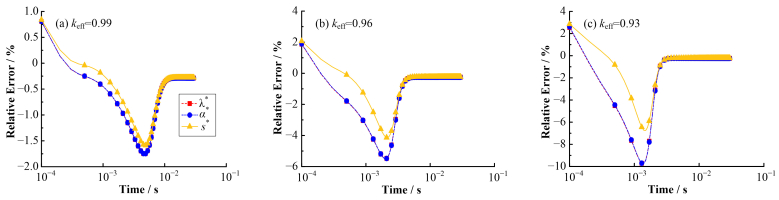
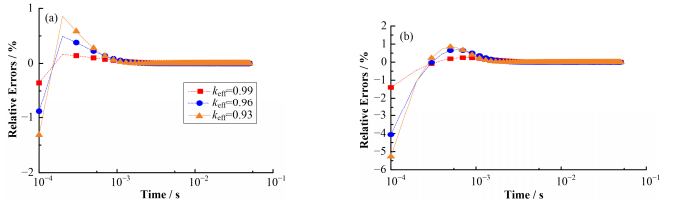
从两种驱动模式的动力学结果中可以看到，在IQS中子动力学中权重函数是影响中子动力学结果的主要因素。对于启堆过程，适合采用共轭λ基波中子通量密度作为权重函数；对于断束工况，采用ADS反应堆稳态共轭中子通量密度作为权重函数，能使IQS中子动力学结果获得更高的精度。图 6、7展示了两种外源驱动模式不同次临界度下最优权重函数模型与其他权重函数模型动力学结果之间的相对误差。从图中可以看到，随着次临界度的加深，λ^*模型、α^*模型与s^*模型计算结果之间的偏差变大，即：λ^*模型在启堆过程中的优势、s^*模型在断束工况下的优势，随着次临界度的加深而愈发明显。

图 6

图 6 启堆过程α*模型(a)、s*模型(b)与λ*模型动力学结果之间的相对误差 Figure 6 The relative errors between the results of α* model (a), s* model (b) and λ* model during starting progress

图 7

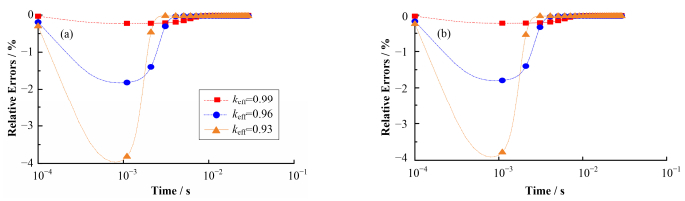
图 7 断束工况λ*模型(a)、α*模型(b)与s*模型动力学结果之间的相对误差 Figure 7 The relative errors between the results of λ* model (a), α* model (b) and s* model in beam loss condition

从物理意义上讲，充当权重函数的“次临界堆中子价值”，其意义可以表达为向次临界堆持续引入强度为1 s^-1的中子源产生的稳定中子数，它强调了次临界堆内某一位置对外源中子的响应：堆内某一位置是否存在外源中子，以及外源中子是否易引发裂变，都将影响权重函数的选取。然而，计算结果所反映的实际情况，与权重函数所具有“次临界堆中子价值”的物理意义似乎是相矛盾的：在启堆过程中，最佳初始形状函数为ADS反应堆稳态中子通量密度，这说明几乎在引入外源驱动的瞬间，外源中子已经对中子通量密度的分布形成稳定的影响，而最适用的权重函数却采用共轭λ基波中子通量密度，其求解方程(14)却不包含共轭外源项，与启堆前反应堆无外源驱动状态是相符合的；断束工况下，外源驱动已经消失，而断束工况下的最佳权重函数采用ADS反应堆稳态共轭中子通量密度，其求解方程(16)依然包含共轭外源项，这说明外源对中子价值的影响依然会维持一段时间。

对于权重函数相对于外源驱动变化的滞后性，可以做出如下解释：外源中子一般是高能中子，不易引发裂变反应，外源中子需要经过慢化才能在堆内某一位置引发裂变反应并对维持临界做出贡献，所以，外源中子对权重函数和中子价值的影响速度远小于外源中子对形状函数影响速度。在启堆时，堆芯内引入外源中子驱动，由于外源中子对中子价值的影响较慢，在启堆后的误差积聚时间段内，外源中子对中子价值的影响尚未扩散至全堆范围，仅覆盖堆芯中央附近位置；在误差积聚时间段内，采用共轭λ基波中子通量密度的权重函数更接近于真实的中子价值分布，能有效降低该时间段内的相对误差，使得整个启堆过程的中子动力学计算精度得到提升。同理，在次临界反应堆失去外源驱动的瞬间，堆内的外源中子不会立刻全部消失，外源中子对中子价值的影响存在一个从堆芯中央向边界的逐渐消退的过程，在误差积聚时间段内，外源中子的影响仍是覆盖堆芯大部分区域的，因此，采用ADS反应堆稳态共轭中子通量密度的权重函数更接近于真实的中子价值分布，能有效降低该时间段内的相对误差，使得整个断束工况的中子动力学计算精度得到提升。

由此可见，权重函数的滞后性现象，主要是由短时间内外源中子影响的非均匀性和误差的大量集聚造成的。因此，在对IQS中子动力学权重函数进行优化时，需要将误差积聚时间堆内外源中子影响的非均匀分布纳入考虑。

通过对两种外源驱动模式IQS中子动力学结果的分析，本文发现，对于启堆过程，采用ADS反应堆稳态共轭中子通量密度作为初始形状函数、共轭λ基波中子通量密度作为权重函数能获得更准确的IQS动力学结果；对于断束工况，适合采用ADS反应堆稳态共轭中子通量密度作为权重函数。

在外源驱动次临界系统中，“次临界堆中子价值”表征的是堆内某一位置对中子的响应；共轭外源项可以理解为：在次临界系统中，单位时间内一个外源中子引发的裂变反应对维持反应堆临界所做出的贡献。权重函数相对于外源瞬变的滞后现象表明，在外源瞬变后的短时间内，外源中子对中子价值和权重函数的影响具有非均匀性，在建立优化的权重函数模型时，需要将共轭外源项的非均匀分布纳入考虑。