† Corresponding author. E-mail:
The current paper presents a thorough study on the pull-in instability of nanoelectromechanical rectangular plates under intermolecular, hydrostatic, and thermal actuations. Based on the Kirchhoff theory along with Eringenʼs nonlocal elasticity theory, a nonclassical model is developed. Using the Galerkin method (GM), the governing equation which is a nonlinear partial differential equation (NLPDE) of the fourth order is converted to a nonlinear ordinary differential equation (NLODE) in the time domain. Then, the reduced NLODE is solved analytically by means of the homotopy analysis method. At the end, the effects of model parameters as well as the nonlocal parameter on the deflection, nonlinear frequency, and dynamic pull-in voltage are explored.
Numerous applications of micro- and nano-electromechanical systems (MEMS/NEMS) have motivated researchers to study their performance in various situations. Because the classical continuum theories cannot consider the size effects in the mechanical analysis of nanostructures,[1–4] some size-dependent continuum theories like Eringenʼs nonlocal elasticity theory,[5] the couple stress elasticity theory,[6] the Gurtin-Murdoch continuum elasticity theory,[7–11] the strain gradient elasticity theory,[12] and the stress-driven nonlocal model[13] were proposed to consider the size effects. In the classical theories, the stress state at a given point is determined only by the strain state at that point, but in Eringenʼs nonlocal elasticity theory, the stress state at a given point is determined by the strain states of all points in the body. The first use of Eringenʼs nonlocal elasticity theory to nanotechnology was proposed by Peddieson et al.,[14] followed by many other researchers.[15–19] One of the important designing considerations in MEMS/NEMS is the pull-in instability.[20] The pull-in instability happens when the internal and applied external forces surpass the elastic restoring force of the nanostructures, leading to contact between the movable and substrate electrodes. When the rate of applied voltage variation is significant, the effect of inertia is considered. In this case, the pull-in instability is referred to as the dynamic pull-in instability.
Once the space of movable and bottom electrodes is less than the plasma wavelength or the absorption wavelength of the ingredient material of surfaces, the intermolecular force is considered as the van der Waals (vdW) attraction. In this situation, there is a small separation regime such that the vdW force is the dominant attraction and it is proportional to the inverse cube of the separation. Nevertheless, when the separation is adequately large (typically above 20 nm) the intermolecular interaction is referred to as the Casimir force.[21] In this case, there is a large separation regime in which the Casimir force is dominant (typically above several tens of nanometers) and it is proportional to the inverse fourth power of the separation 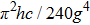
In the past few years, many researchers have focused on the pull-in instability of nanoplates. For instance, based on a modified continuum model, Ansari et al.[34] studied the size-dependent pull-in behavior of electrostatically and hydrostatically actuated rectangular nanoplates considering the surface stress effects. Ebrahimi and Hosseini[35] investigated the effect of temperature on pull-in voltage and nonlinear vibration of nanoplate-based NEMS under hydrostatic and electrostatic actuations. Mirkalantari et al.[36] studied the pull-in instability of rectangular nanoplates based on the strain gradient theory taking the surface stress effects into account. Shokravi[37] analyzed the dynamic pull-in of viscoelastic nanoplates under the electrostatic and Casimir forces. The interested reader is referred to Refs.[38–44].
Moreover, different methods have been used for the vibration analysis of rectangular nanoplates. For example, Aghababaei and Reddy[45] presented the Navier solutions for the vibrations of rectangular plates based on the nonlocal third-order shear deformation plate theory. Also, Pradhan and Phadikar[46] used the same solution technique for addressing the vibration problem of rectangular plates with simply-supported boundary conditions in the context of Eringenʼs nonlocal model, the classical and first-order shear deformation plate theories. Another application of the Navier-type method to the vibration problem of nonlocal plates can be found in Ref. [47]. Aksencer and Aydogdu[48] employed the Levy-type solution method for the vibration analysis of nanoplates based on the nonlocal elasticity theory. Ansari et al.[49,50] used the generalized differential quadrature method to numerically solve the free vibration problem of rectangular Mindlin-type plates with various boundary conditions. The Galerkin method was applied by Shakouri et al.[51] for the vibrational analysis of nonlocal Kirchhoff plates with different edge supports.
The classical analytical methods cannot handle the strongly nonlinear differential equations. In this regard, Liao[52] developed an efficient technique called the homotopy analysis method (HAM), which can be adopted for solving ordinary and partial differential equations with different nonlinearities. For example, Samadani et al.[53] applied HAM for the pull-in and nonlinear vibration analysis of nanobeams using a nonlocal Euler-Bernoulli beam model. Moghimi Zand and Ahmadian[54] used HAM in studying the dynamic pull-in instability of microsystems. Also, Miandoab et al.[55] utilized this method for the forced vibration analysis of a nano-resonator with cubic nonlinearities.
In the present paper, HAM is used to study the static and dynamic pull-in instabilities of rectangular nanoplates using the nonlocal Kirchhoff plate theory. The rest of paper is organized as follows: In Sec.
Based on Eringenʼs nonlocal elasticity theory,[3] the stress at a reference point depends on the strain at all points in the body. The constitutive equation of the nonlocal elasticity can be written as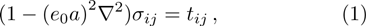
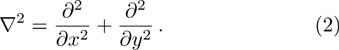
Based on the Kirchhoff thin plate theory, the strains in the plate are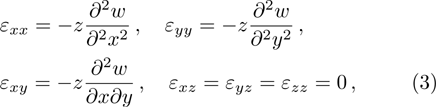
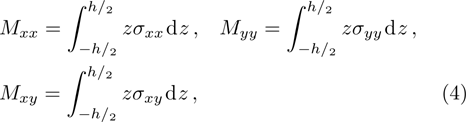
Under plane stress conditions, one has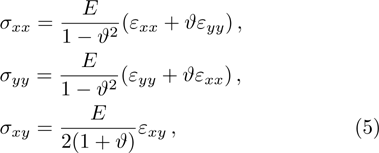
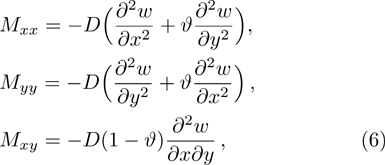
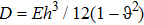
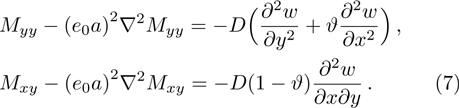
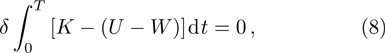
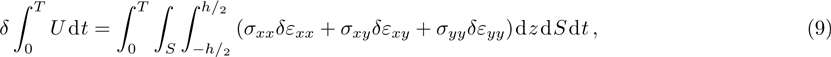
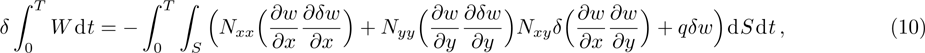
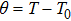

The first variation of kinetic energy is
By inserting Eqs. (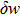
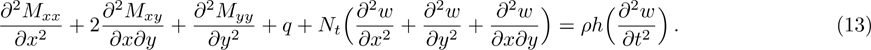
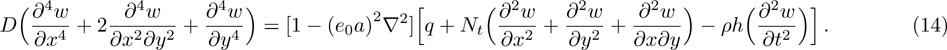
Note that the governing equation of local model is obtained by setting 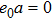
A schematic of nanoelectromechanical rectangular plate with length la and width lb, including a pair of parallel electrodes with the distance g is given in Fig.
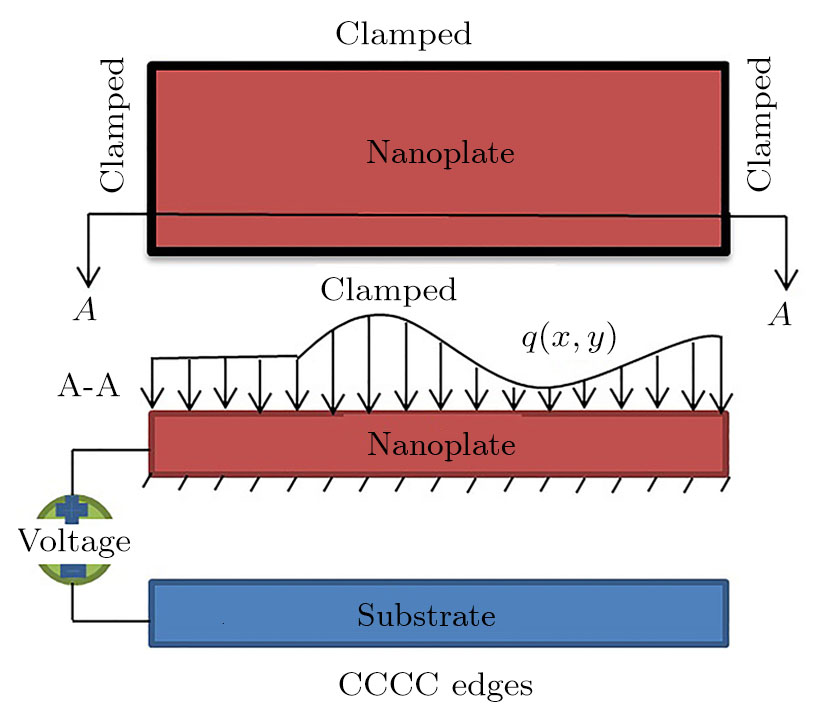 | Fig. 1. Schematic of fully clamped nanoelectromechanical rectangular plates under intermolecular, hydrostatic and thermal actuations. |
It is noted that the movable electrode pulls down the fixed electrode by applying the DC voltage between two electrodes. Once the applied voltage approaches the critical point (pull-in voltage), the structure becomes unstable.[57]
The electrostatic force per unit area of nanoplate can be described as[39]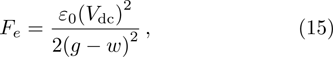
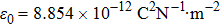
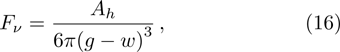
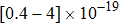
In the following analyses, it is assumed that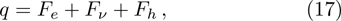
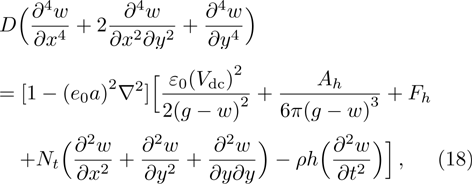
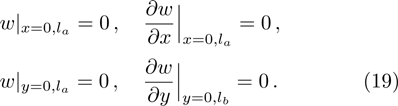
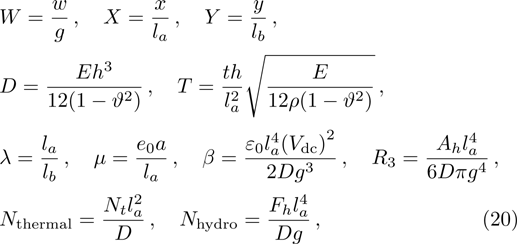
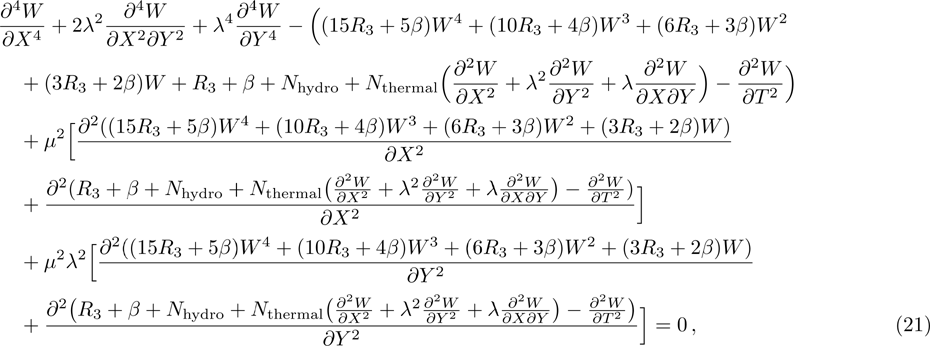
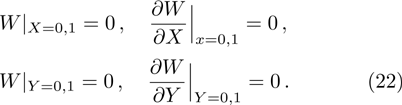
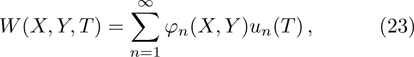
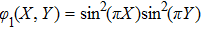
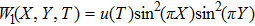
By inserting 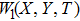
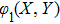
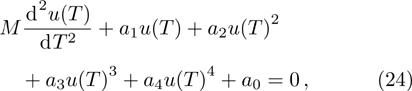
Now, using the transformation 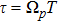
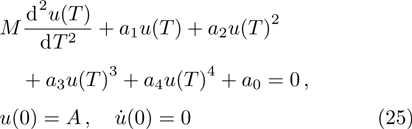
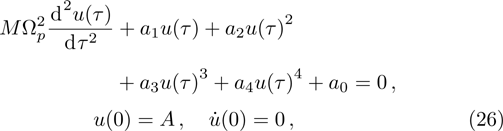
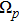

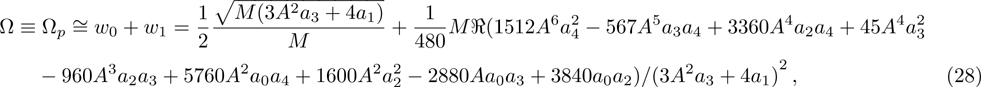
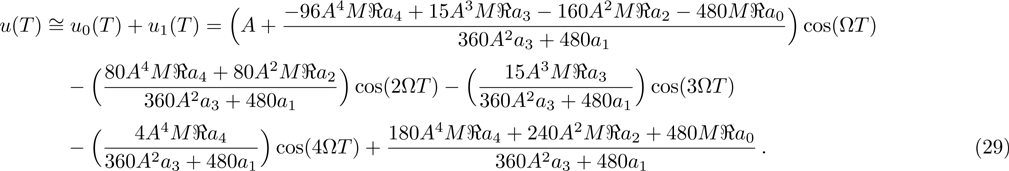
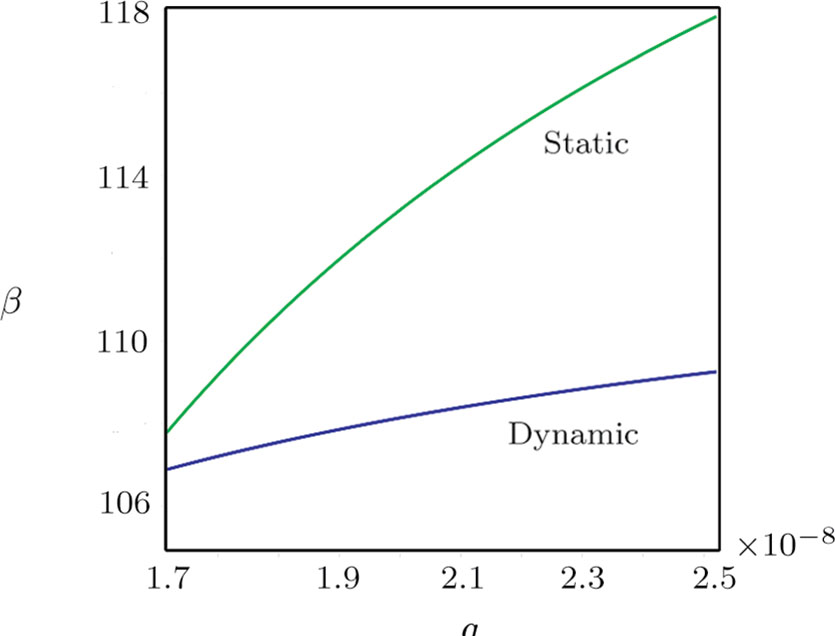
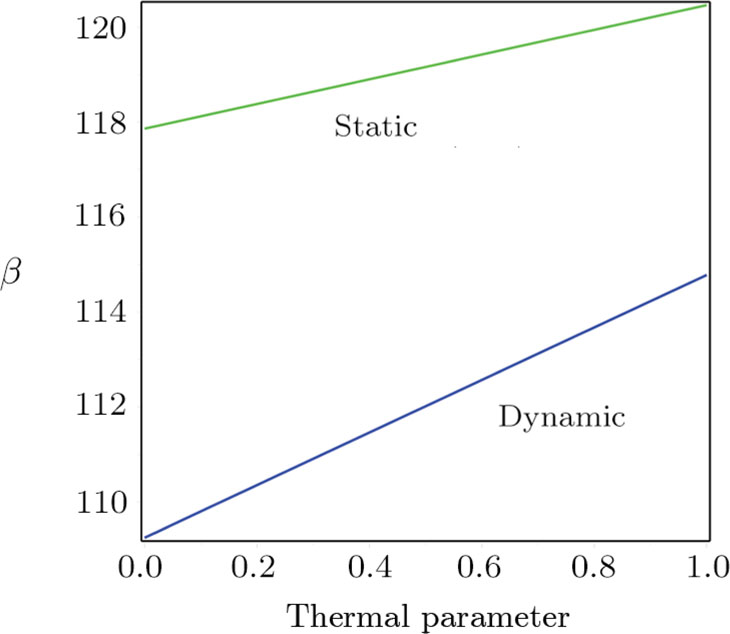
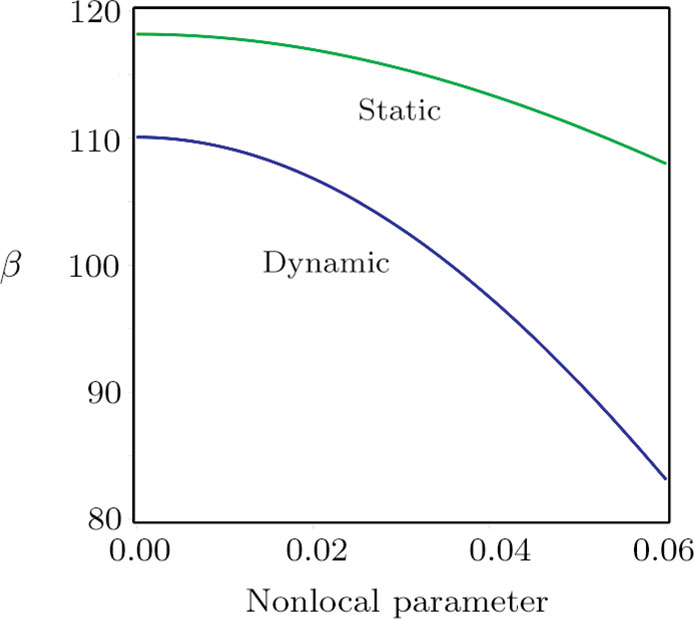
The current section provides numerical results to show the effects of intermolecular, hydrostatic, and thermal actuations as well as the nonlocal parameter μ on the deflection, nonlinear frequency, and Vpdyn. For producing the results, the following parameters are selected: h = 21 nm, 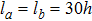
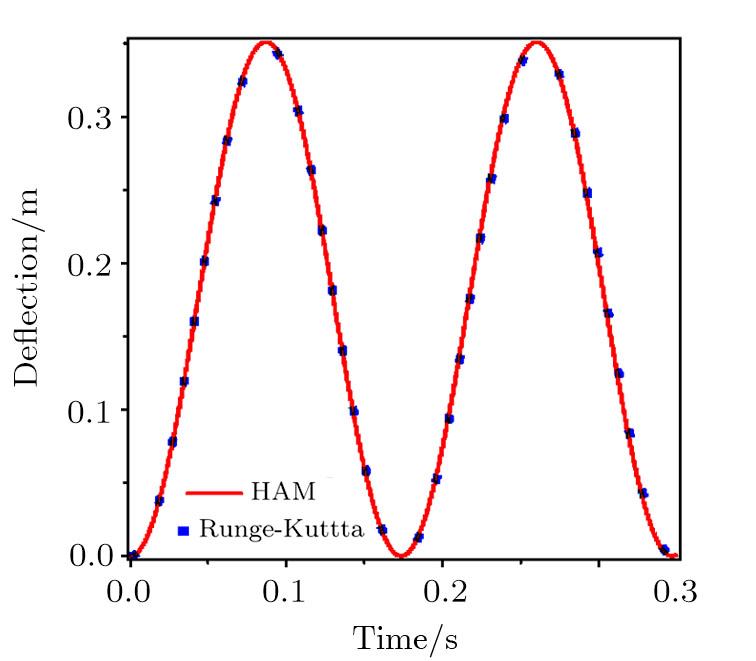
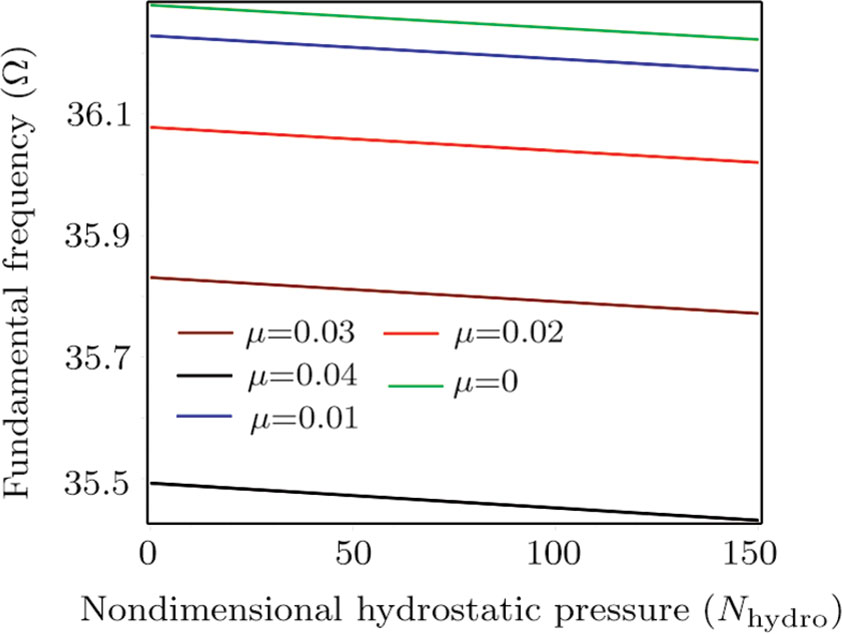
In Fig.
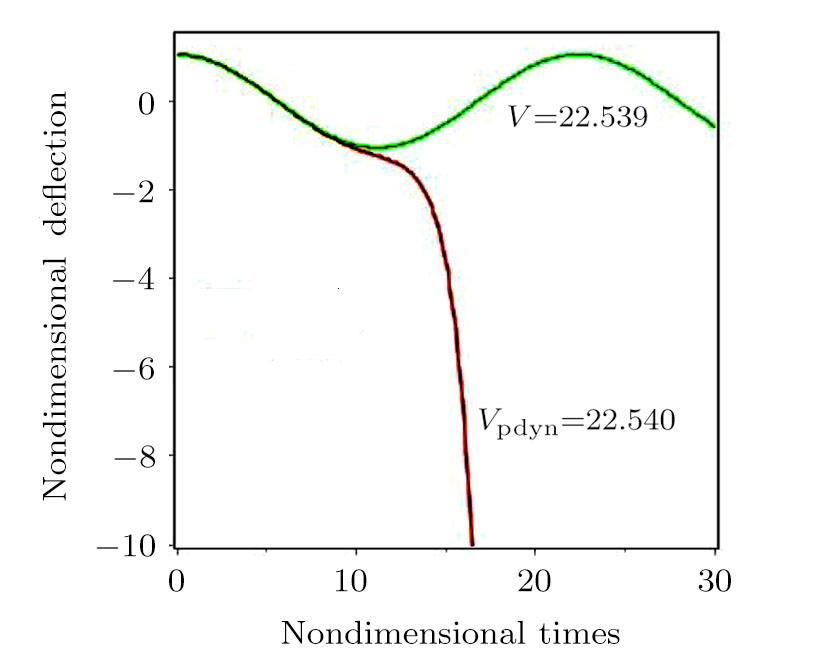
Figure
Figure
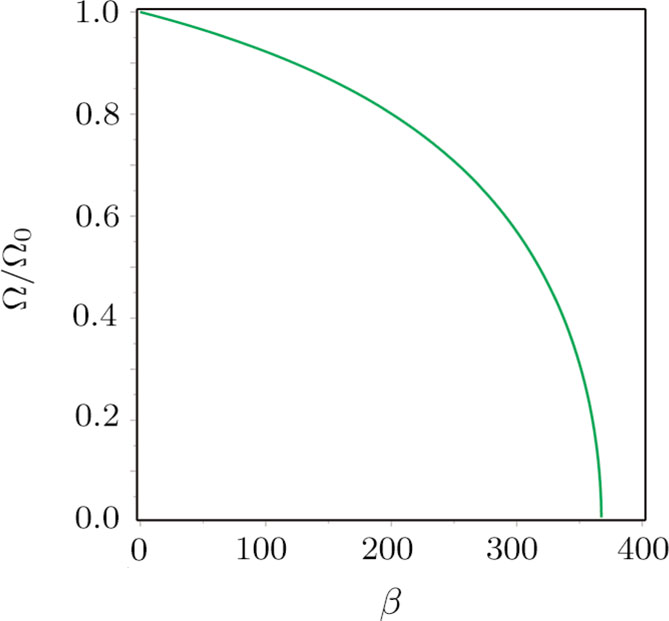 | Fig. 4. Relation between the normalized fundamental frequency and the electrostatic force parameter. |
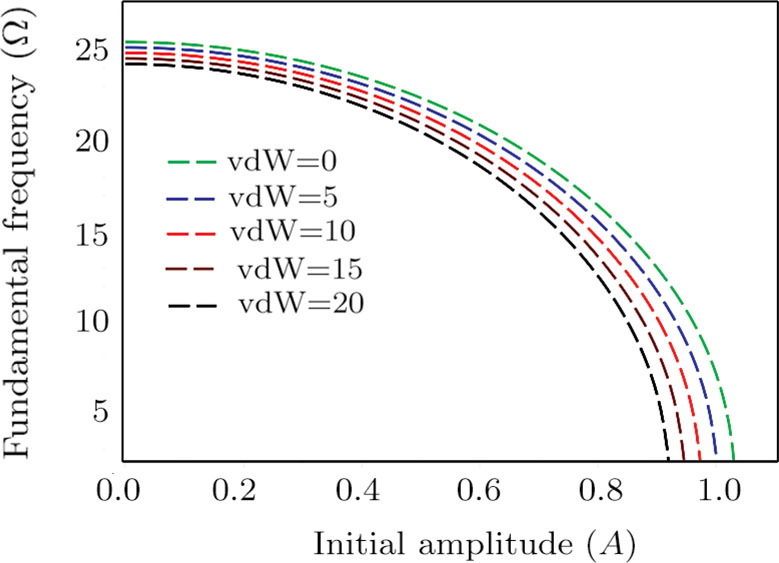
Figure
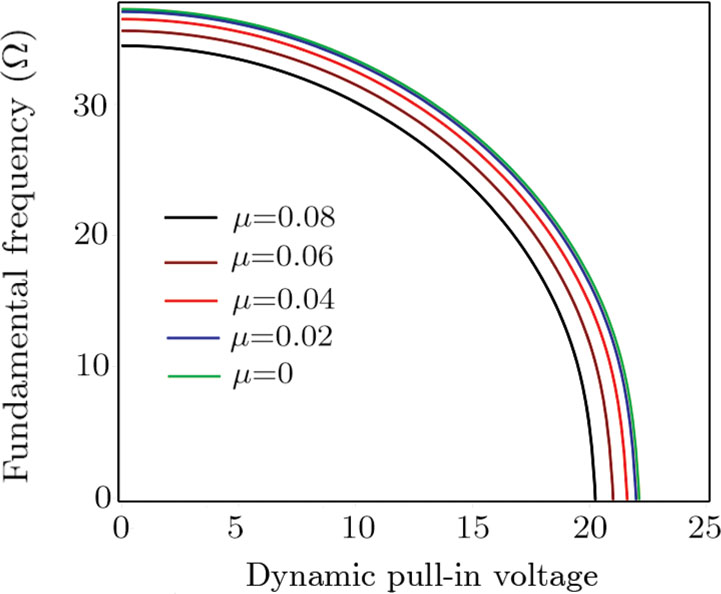
The variations of fundamental frequencies against Vpdyn are illustrated in Fig.
Figure
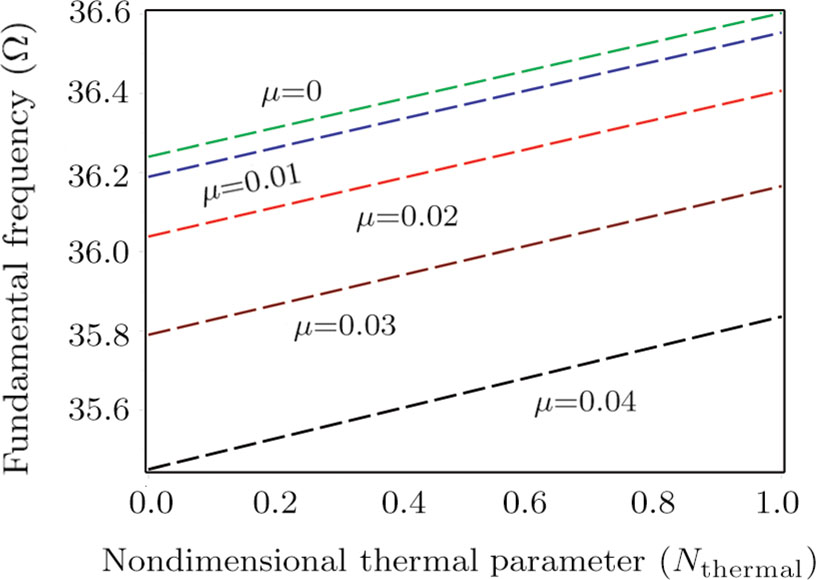
The variations of fundamental frequencies against the nondimensional thermal parameter are illustrated in Fig.
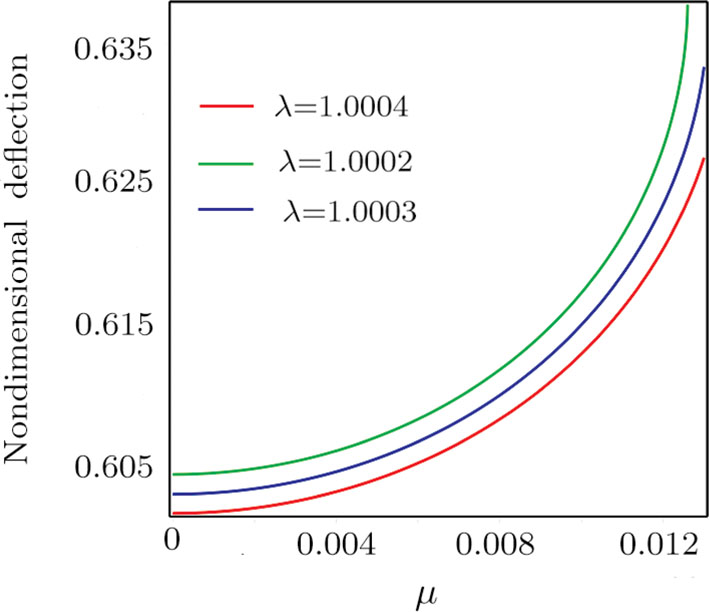
Figure
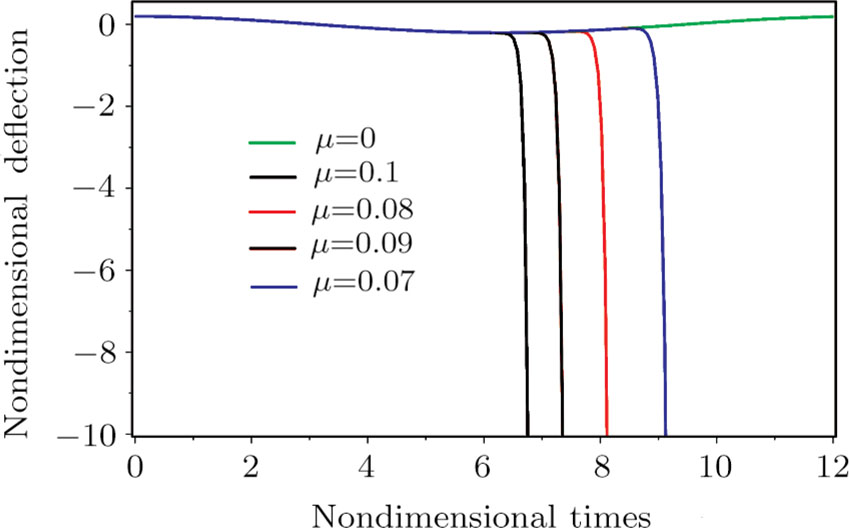
The influence of 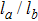
In the present research, the dynamic pull-in of CCCC plate-type nanosensor, subjected to electrostatic, intermolecular, hydrostatic and thermal actuations was analyzed based on the nonlocal theory. GM was utilized for reducing the governing NLPDE to an NLODE in the time domain. HAM was also applied for solving the NLODE. The outcomes reveal that:
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] |