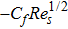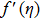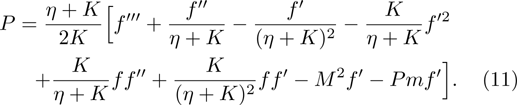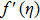† Corresponding author. E-mail:
This research is made to visualize the boundary layer flow by a curved stretching sheet embedded in porous medium. The geometry is bended (curved), therefore the curvilinear coordinates are used to model the present problem. Fluid is electrically conducting with the presence of uniform magnetic field. The governing non-linear partial differential equation reduces to non-linear ordinary differential equations by using the dimensionless suitable transformations. The numerical solutions are obtained by using the method bvp4c from MATLAB. The effects of curvature parameter, non-dimensional magnetic parameter, and porosity parameter on the velocity field and skin friction coefficient are examined. The skin friction profile enhances with enhancing the values of porosity and magnetic parameter. Comparison of the present results with the existing results in the literature for the flat surface is also given.
u,v
velocity components
B0
constant magnetic field
r,s
curvilinear coordinates
σ
electrical conductivity
μ
fluid dynamic viscosity
M
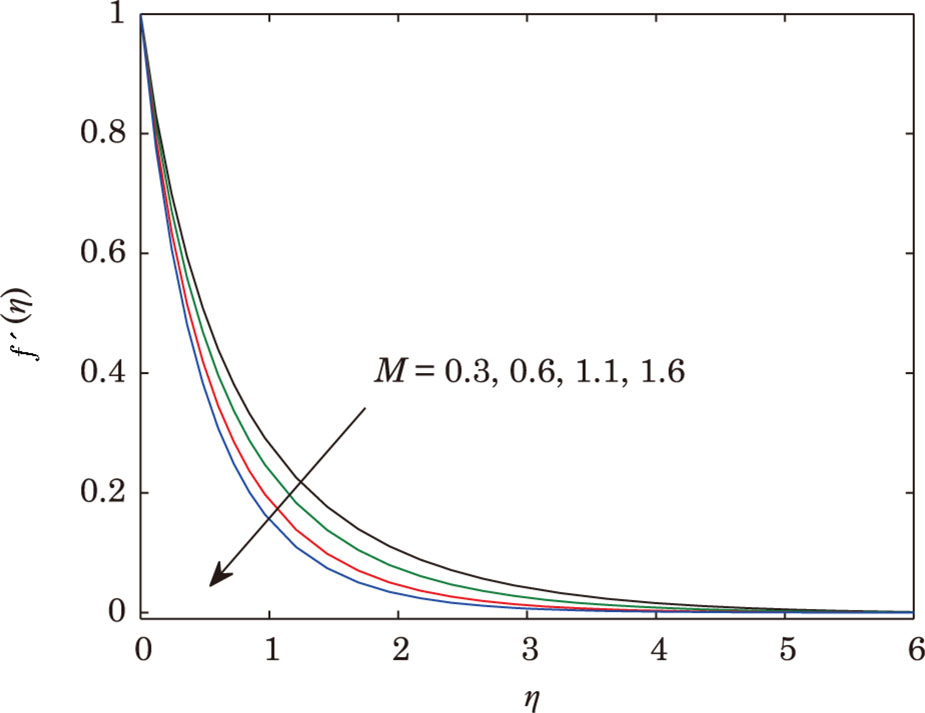
magnetic parameter
ρ
fluid density
Pm
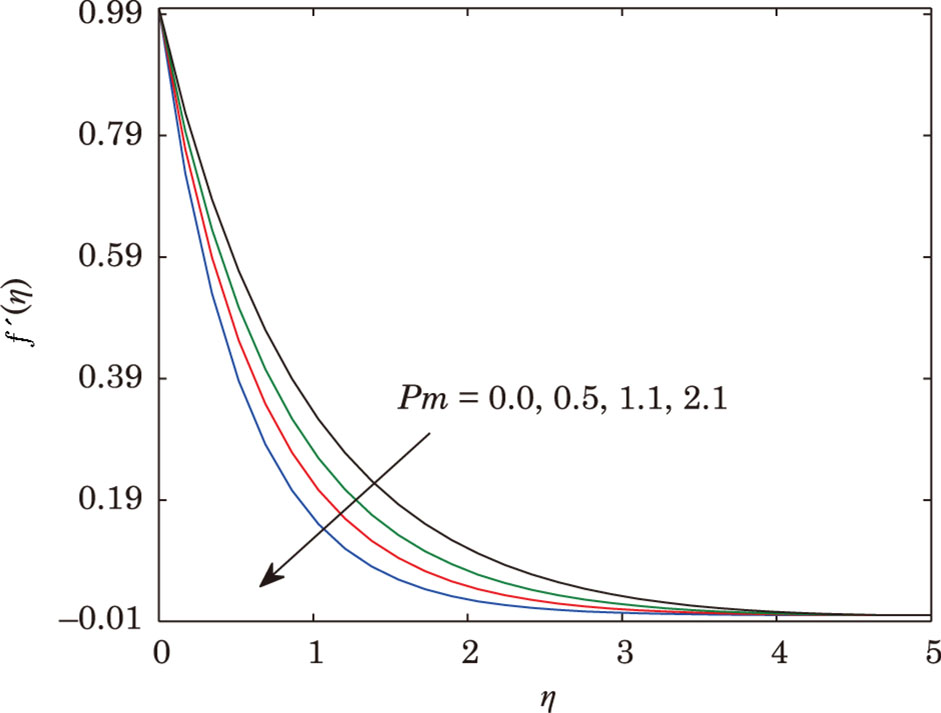
porosity parameter
R
dimensionless radius of curvature
K
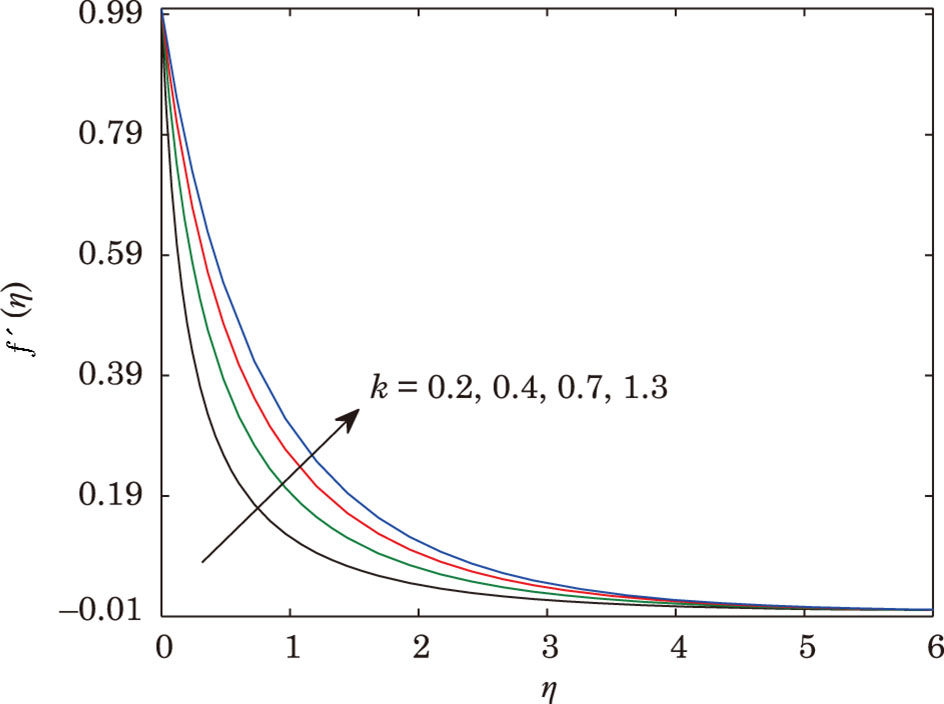
parameter of curvature
p
pressure
τrs
wall shear stress
υ
kinematic viscosity
Cf
surface drag force
k
permeability of porous medium
η
dimensionless variable
c
positive stretching constant
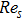
local Reynold number
P
dimensionless pressure
μ
fluid dynamic viscosity
The viscous boundary layer flow caused by a stretching sheet moving with a certain velocity often occurs in many industrial and engineering processes. These flows have extensive applications in industries, for example in the drawing of plastic films or in the extrusion of polymer sheet from a die. During the production of the respective sheets, the melt issues from a slit are accordingly stretched to get the required thickness. The mechanical characteristic of the subsequent product depends on the cooling and stretching rates in the process. Crane[1] proposed the steady two-dimensional flow of a viscous fluid past a stretching surface. An exact closed-form solution was obtained for Craneʼs problem in fluid dynamics.Further, the work of Crane was extended in several ways to add other physical features like blowing or suction, magnetic field, and heat transport phenomenon, etc. Mehmood et al.[2] incorporated the heat transport phenomena in a flow of Jeffrey nanofluid past a stretched plate. Muhammad et al.[3] investigated the heat transfer phenomenon in the presence of thermal stratification of ferrofluid over a stretching surface. Muhammad et al.[4] utilized the Cattaneo-Christov heat flux model to discuss the squeezed flow in nanofluid over a stretching sheet. Zeeshan et al.[5] demonstrated the heat transfer in the flow of ferrofluid via stretching surface. Maqbool et al.[6] used a stretching surface to explore the Falkner-Skan boundary layer flow.
In fluid mechanics, porous medium is a substance containing voids (pores). The voids are filled usually with a fluid. The skeletal portion of the substance is called frame. The frame is typically solid, but structures like foams are analyzed using the concept of porous media. The porous medium is incorporated by its porosity. Porous medium has also the properties of permeability, electrical conducting, tortuosity, and tensile strength. The deviation of these properties of porous medium is complex due to the pores structure and media porosity. Certain natural materials and substances including rocks and soil (e.g. petroleum resources, aquifers), biological tissues (e.g. wood, bones, cork), zeolites and several other man made substances like cements and ceramics can be considered as porous media. In this direction, lots of work exists in the literature. Sheikholeslami et al.[7] scrutinized the heat transfer flow past a permeable stretching wall embedded in porous medium. The Numerical study of nanofluid transportation in porous media with external magnetic source is established by Sheikholeslami and Ganji.[8] Nadeem and Muhammad[9] indicated the flow dripping with porous medium using Cattaneo-Christov heat flux model. Debasish[10] symbolized the non-Newtonian effect on hydromagnetic stratified dusty fluid flow along a porous media. Devakar et al.[11] examined fully developed flow in a straight uniform square duct of non-Newtonian fluids saturated in a porous medium. Ellahi et al.[12] expressed the heat transfer phenomenon in a third grade fluid embedded in porous medium. Vajravelu[13] taken stretching surface to discuss heat transfer flow embedded in porous medium.
With rapid progress of modern engineering technology, the curved stretching has got extensive attention due to its various applications in transportation, industrial, and electronics. Sanni et al.[14] obtained the numerical solution of viscous fluid saturated in curved stretching sheet. In the presence of magnetic field, the viscous fluid flow over a curved sheet were established by Abbas et al.[15] Nadeem et al.[16] indicated the chemically reactive species in the flow of Maxwell fluid over a stretching channel. Hayat et al.[17] utilized the curved stretching sheet to examine the convective flow with chemical reaction. Rosca and Pop[18] explored the unsteady boundary layer flow along a permeable curved shrinking/stretching surface. Hayat et al.[19] analyzed the homogeneous-heterogeneous reaction past a curved sheet with magnetohydrodynamic. In all these articles the stretching is curved, and to the best of our knowledge there is not a single article in the existing literature regarding the stretching flow in presence of porous medium and magnetohydrodynamic past a curved surface. In this article, we present a numerical study to obtain the solution of non-linearly ordinary differential equation by using bvp4c from MATLAB. The graphical behavior of sundry parameters is presented. Some application about stretching sheet, porous media, and magnetic field is given in Refs.[20–28].
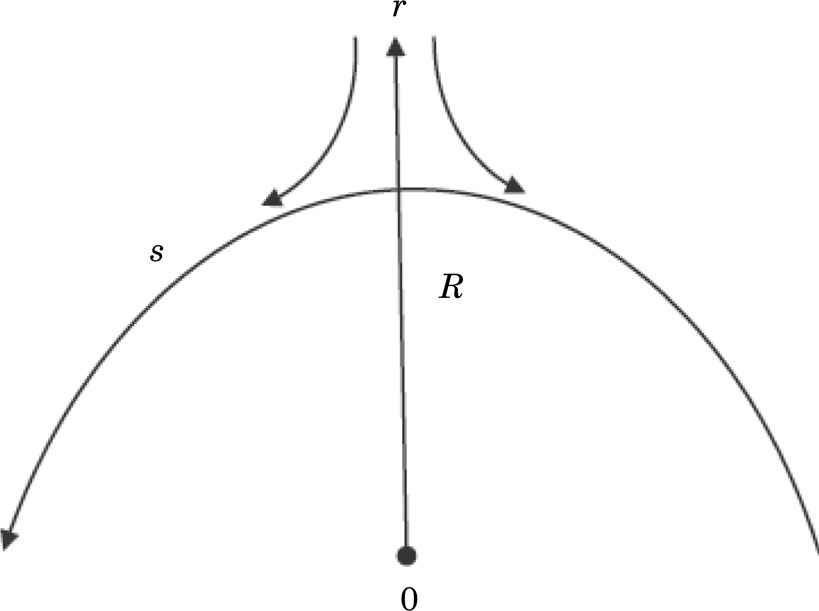
Consider the steady two-dimensional and an incompressible viscous fluid past a curved stretching channel coiled in a circle of radius R about the curvilinear coordinates r and s, as shown in Fig.
Under the boundary layer approximation, the governing equations for the flow problem are given as:

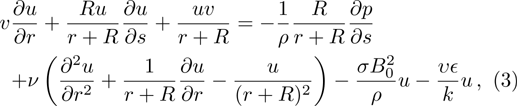
For the velocity profile boundary conditions are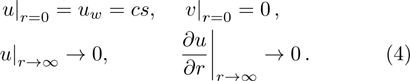
Here we introduce the following dimensionless variables as: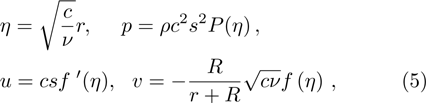
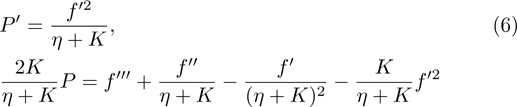
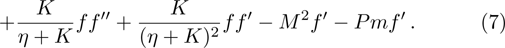
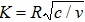
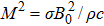
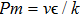
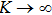
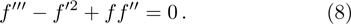
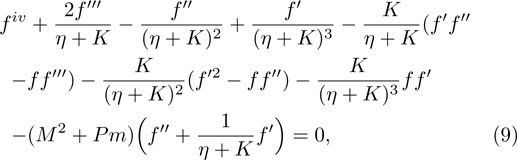
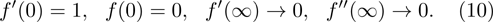
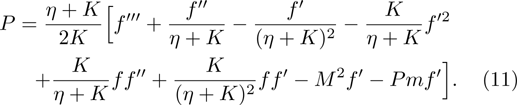

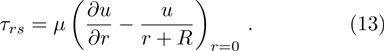
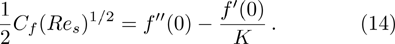
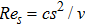
The numerical method bvp4c from MATLAB is utilized to solve the numerical solution for the non-linear ordinary differential Eq. (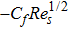
| Table 1.
The comparison of Skin friction with previous result Abbase et al.[15] . |
| Table 2.
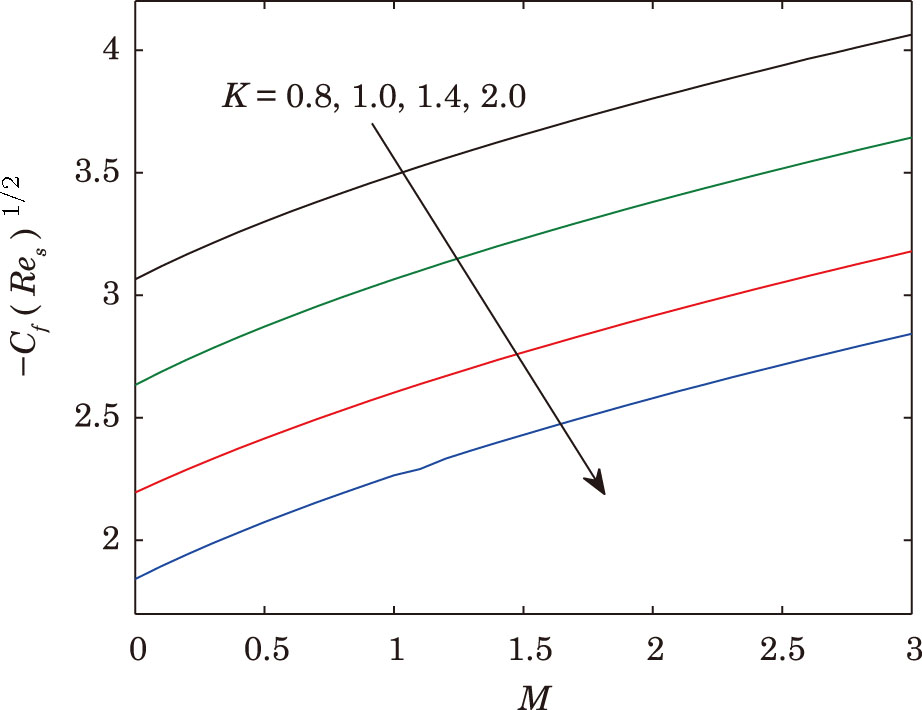
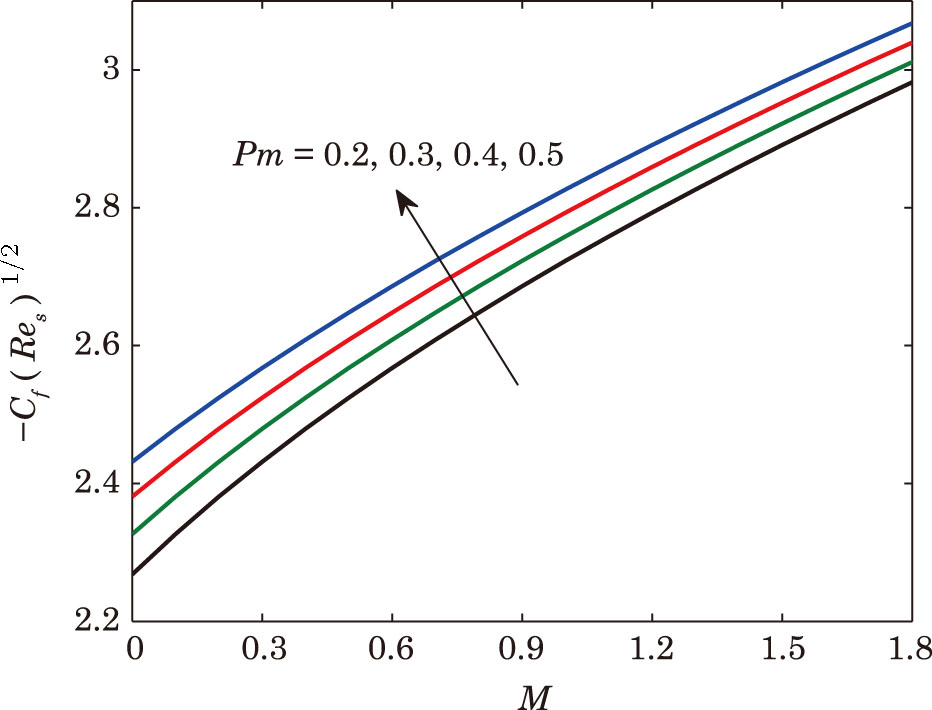
The value of skin friction for different values of parameters. . |
Figure 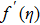
It is found that the fluid velocity has inverse relation with porosity parameter, i.e. for enlarging values of porosity parameter the fluid velocity becomes thinner. In fact porous medium presence increases the resistance to fluid motion, which produces reduction in fluid velocity and related momentum layer thickness. The values assign to remaining parameters are K = 0.1 and M = 0.3.
The mathematical expression for skin friction coefficient is given in Eq. (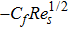
The property of the magnetic field in a viscous fluid over a steady curved stretching surface embedded in the porous medium is investigated. The following conclusion is made.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] |