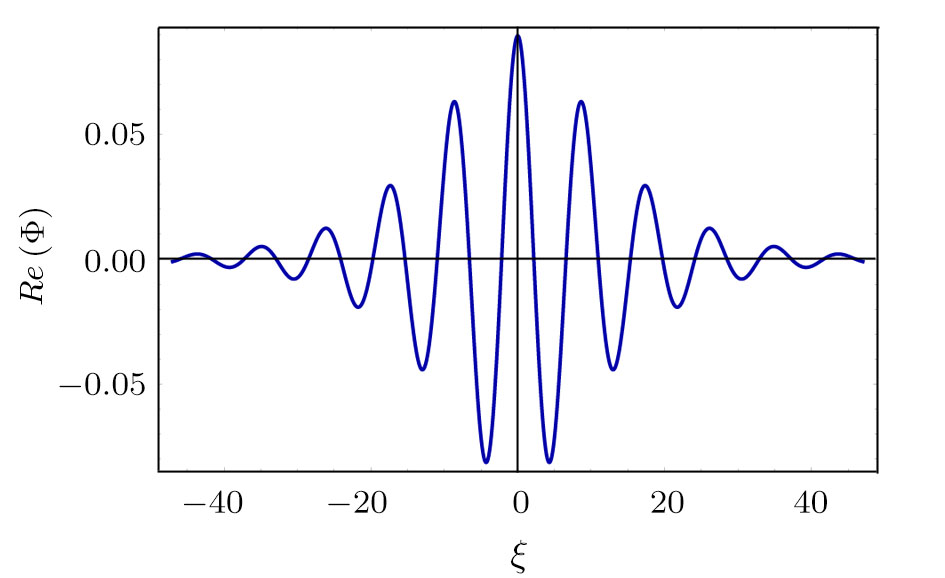
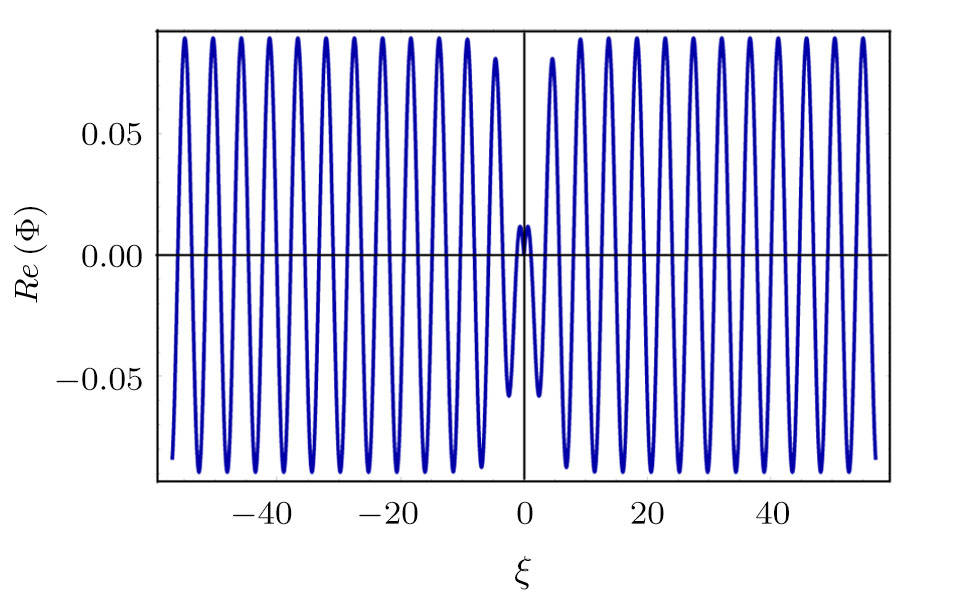
† Corresponding author. E-mail:
The nonlinear propagation of the dust-acoustic bright and dark envelope solitons in an opposite polarity dusty plasma (OPDP) system (composed of non-extensive q-distributed electrons, iso-thermal ions, and positively as well as negatively charged warm dust) has been theoretically investigated. The reductive perturbation method (which is valid for a small, but finite amplitude limit) is employed to derive the nonlinear Schrödinger equation. Two types of modes, namely, fast and slow dust-acoustic (DA) modes, have been observed. The conditions for the modulational instability (MI) and its growth rate in the unstable regime of the DA waves are significantly modified by the effects of non-extensive electrons, dust mass, and temperatures of different plasma species, etc. The implications of the obtained results from our current investigation in space and laboratory OPDP medium are briefly discussed.
Now-a-days, the study of dusty plasma (DP) is one of the most rapidly growing branches in plasma physics due to their existence in space, viz., planetary rings,[1] cometary tails,[2] Jupiterʼs magnetosphere,[2] lower part of the Earthʼs atmosphere[1] and also in laboratory plasmas.[3–7] The DP have generally considered to be an ensemble of negatively charged dust grains, free electrons, and ions. However, the co-existence of opposite polarity (OP) dust grains in plasmas introduces a new DP model called OP DP (OPDP) whose main constituent species are positively and negatively charged warm massive dust grains.[2,6] The exclusive property of this OPDP, which makes it completely unique from other plasmas (viz., electron ion and electron-positron plasmas), is that the ratio of the size of positively charged dust grains to that of negatively charged dust grains can be smaller[8] or larger[9] or equal to unity.[9] There are three main processes by which dust grains become positively charged: (a) Secondary emission of electrons from the surface of the dust grains; (b) Thermionic emission induced by the radiative heating; (c) Photoemission in the presence of a flux of ultraviolet photons.[1,10]
The researchers have focused on wave dynamics, specifically, dust-acoustic (DA) waves (DAWs), dust-acoustic rogue waves (DARWs), and dust ion-acoustic waves (DIAWs) in understanding electrostatic density perturbations and potential structures (viz., shock, soliton, envelope solitons,[11–12] and rogue waves[13–15]) in DP. Rao et al.[14] first theoretically predicted the existence of very low frequency DAWs (where the inertia is provided by the dust mass and restoring force is provided by the thermal pressure of electrons and ions) in comparison with the electron and ion thermal velocities and this theoretical prediction has been conclusively verified by Barken et al.[4] There is also direct evidence for the co-existence of both positively and negatively charged dust grains in different regions of space plasmas (viz., cometary tails,[2] upper mesosphere,[2] and Jupiterʼs magnetosphere,[10] etc.) and laboratory devices (viz., direct current and radio-frequency discharges,[1] plasma processing reactors,[16] fusion plasma devices, and solid-fuel combustion products,[1] etc). The novelty of this OPDP has attracted numerous authors[17–21] to investigate the linear and nonlinear propagation of electrostatic waves. Sayed and Mamun[2] studied the finite solitary potential structures that exist in OPDP. El-Taibany[17] examined the DAWs in inhomogeneous four component OPDP, and observed that only compressive soliton is created corresponding to fast DA mode.
In space and astro-physical situations, if the plasma species move very fast compared to their thermal velocities[22] then the Maxwellian distribution is no longer valid to explain the dynamics of these plasma species. For that reason, Tsallis proposed the non-extensive statistics,[23] which is the generalisation of Boltzmann-Gibbs-Shannon entropy. The importance of Tsallis statistics is that it can easily describe the long range interactions of the electron-ion in DP system.[13–15] The research regarding modulational instability (MI) of DAWs in nonlinear and dispersive mediums has been increasing significantly due to their existence in astrophysics, space physics[11–15] as well as in application in many laboratory situations.[11] A large number of researchers have used the nonlinear Schrödinger equation (NLSE), which governs the dynamics of the DAWs, to study the formation of the envelope solitons or rogue waves[13–15] in DP. Bains et al.[13] investigated the MI of the DAWs in non-extensive DP. Moslem et al.[14] have studied the MI of the DAWs in three component DP in presence of the non-extensive electrons and ions, and have found that the threshold wave number (kc) increases with q. Duan et al.[19] have investigated the criteria for MI of the DAWs and the formation of envelope solitons in OPDP. Zaghbeer et al.[20] have reported DARWs in a four component OPDP. Gill et al.[21] have studied MI of DAWs in a four component OPDP, and have found that the presence of positive dust grains significantly modify the domain of the MI and localized envelope solitons. To the best knowledge of the authors, no attempt has been made to study the MI and corresponding dark and bright envelope solitons associated with the DAWs in a four component OPDP in presence of OP warm adiabatic dust grains. The aim of the present investigation is therefore to extend the work of Gill et al.[21] by examining the conditions for the MI of the DAWs (in which inertia is provided by the OP warm dust masses and restoring force is provided by the thermal pressure of q-distributed electrons and iso-thermal ions) in four component OPDP.
The manuscript is organized as the following fashion: The governing equations of our plasma model are provided in Sec.
In this paper, we consider a collisionless, fully ionized, unmagnetized four component dusty plasma system composed of q-distributed electrons (charge −e, mass me), iso-thermal ions (charge + e, mass mi) and inertial warm negatively charged dust grains (charge 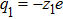
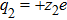
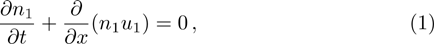
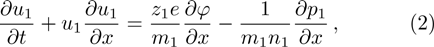
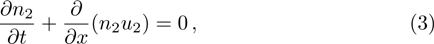
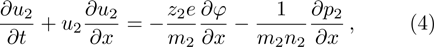
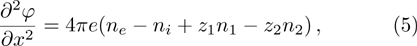
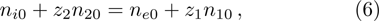
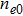
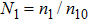
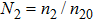
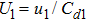
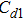
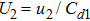
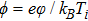
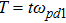
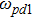
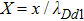
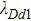
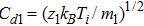
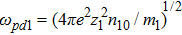
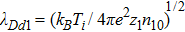
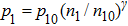
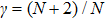
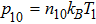
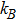
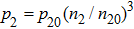
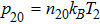

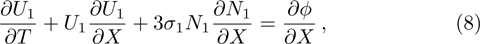

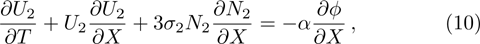
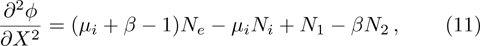
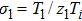
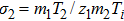
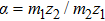
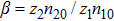
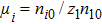
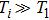
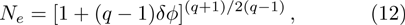
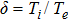
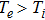
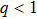
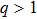

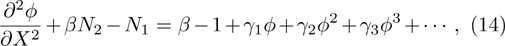
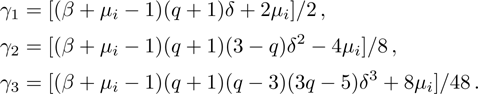
We will use the reductive perturbation method (RPM) to derive the NLSE for studying the MI of the DAWs in OPDP. Now, the stretched co-ordinate[15] can be defined as

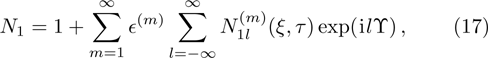
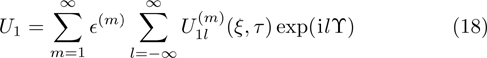
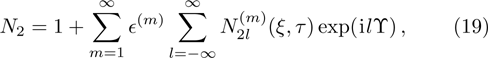
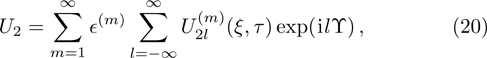
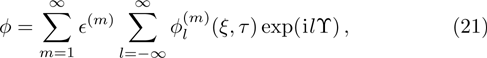
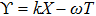
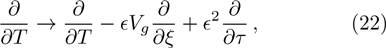
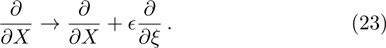

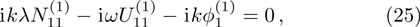

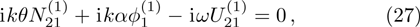
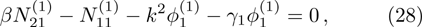
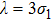
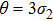




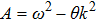
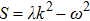

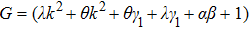
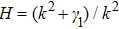
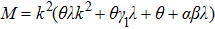
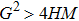
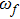
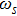
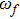
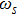
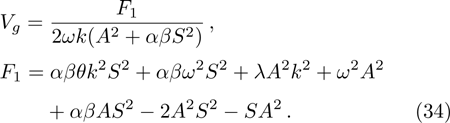
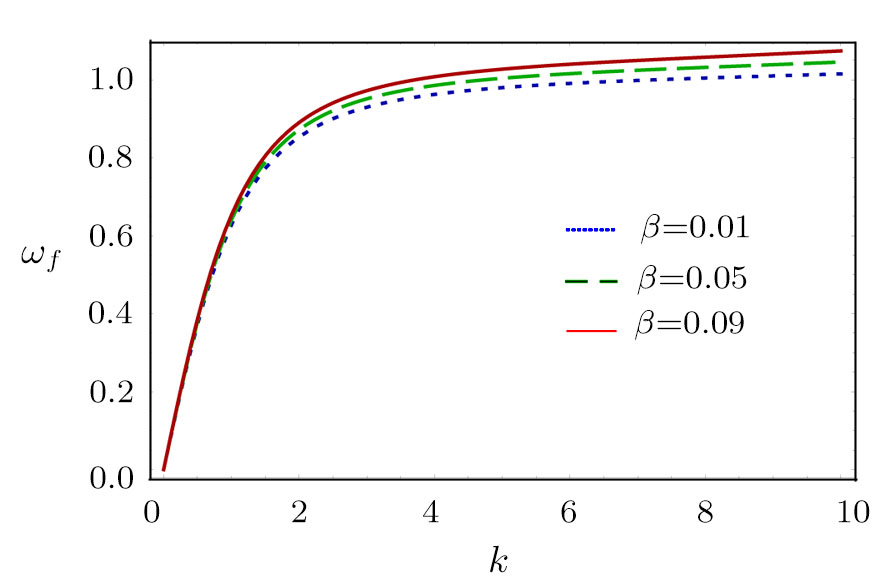 | Fig. 1 The variation of ωf with k for different values of β, along with α = 1.2, δ = 0.3, μi = 1.4, σ1 = 0.0001, σ2 = 0.001, and q = 1.8. |
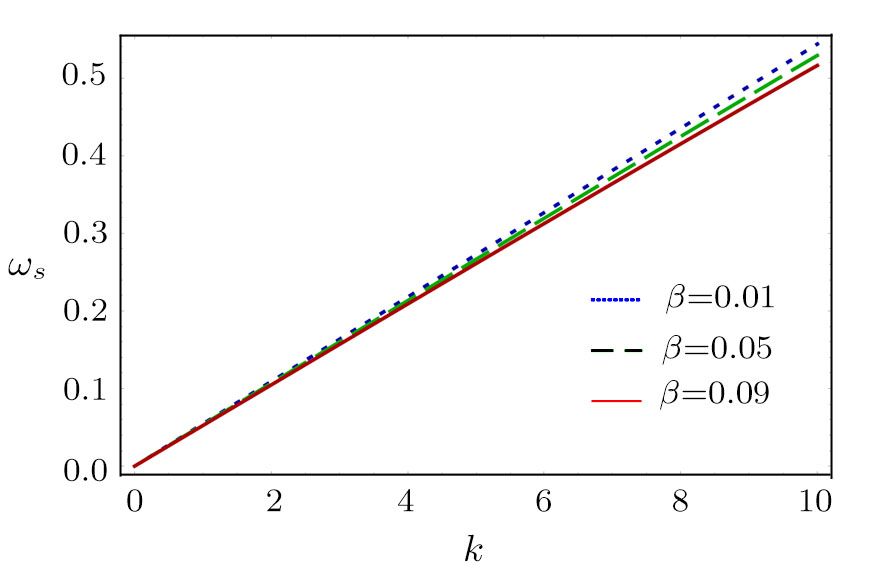 | Fig. 2 The variation of 
|
From the next order of ϵ, we can get the second-harmonic mode of the carrier wave with m = 2 and l = 2 as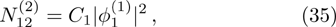

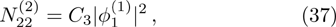


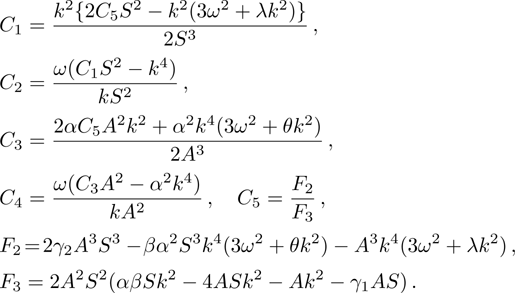
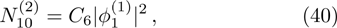

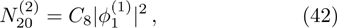

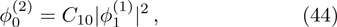
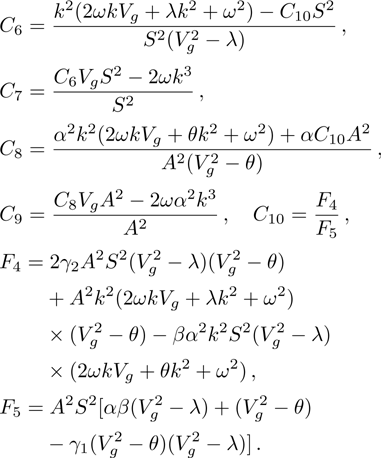
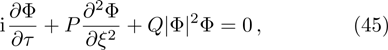
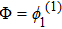
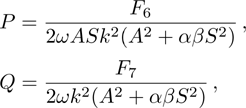
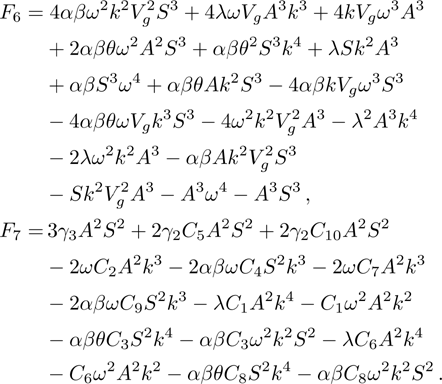
The DAWs are modulationally stable against external perturbation when 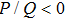
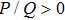
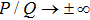
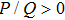
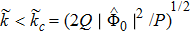
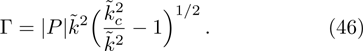
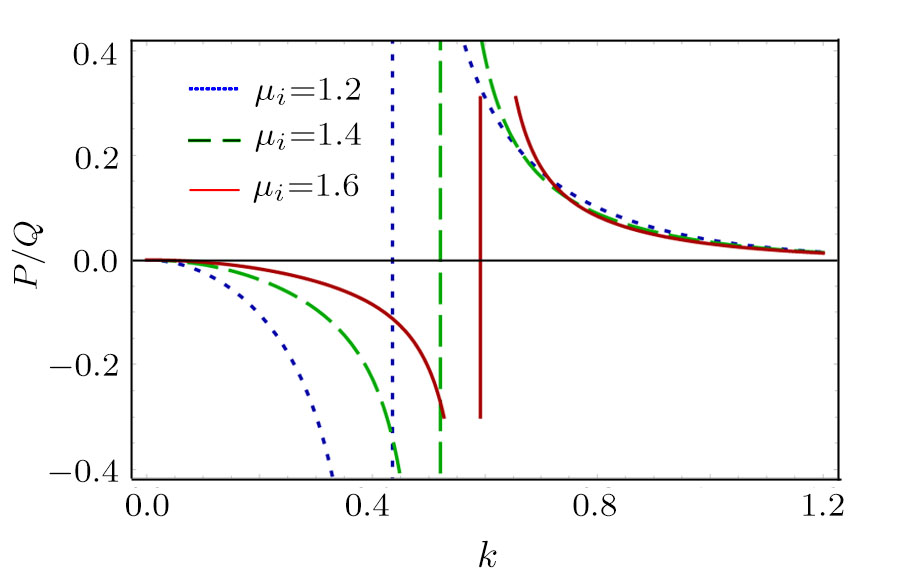 | Fig. 3 The variation of P/Q with k for different values of μi, along with α = 1.2, β = 0.07, δ = 0.3, σ1 = 0.0001, σ2 = 0.001, q = 1.8, and ωf. |
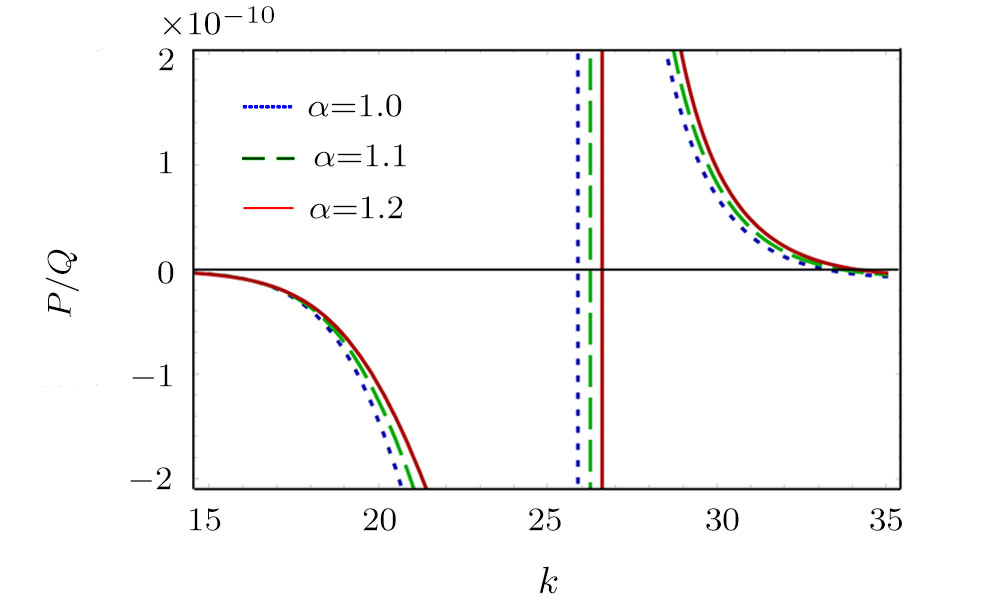 | Fig. 4 The variation of P/Q with k for different values of α, along with β = 0.07, δ = 0.3, μi = 1.4, σ1 = 0.0001, σ2 = 0.001, q = 1.8, and ωs. |
Now, we have graphically shown how the Γ varies with 
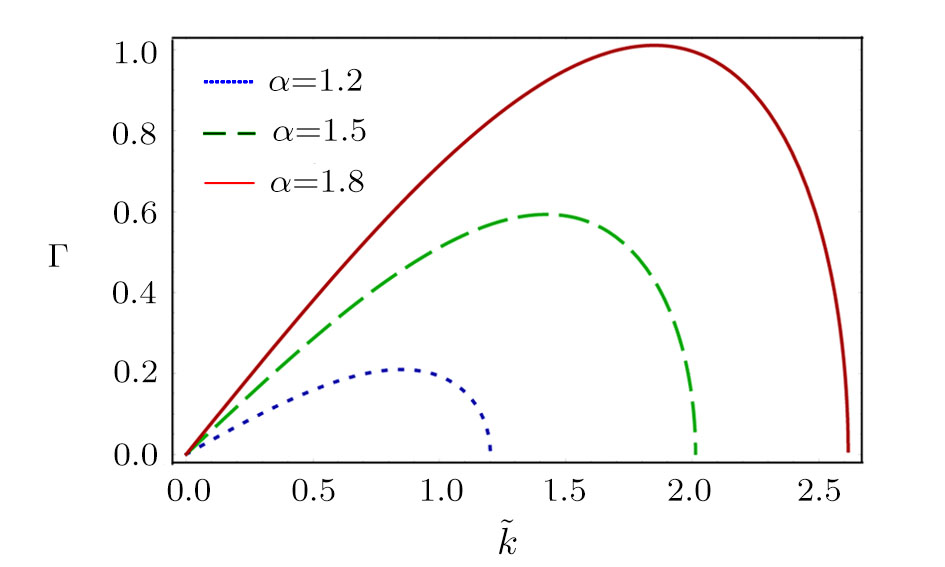 | Fig. 5 The variation of Γ with 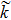
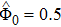
|
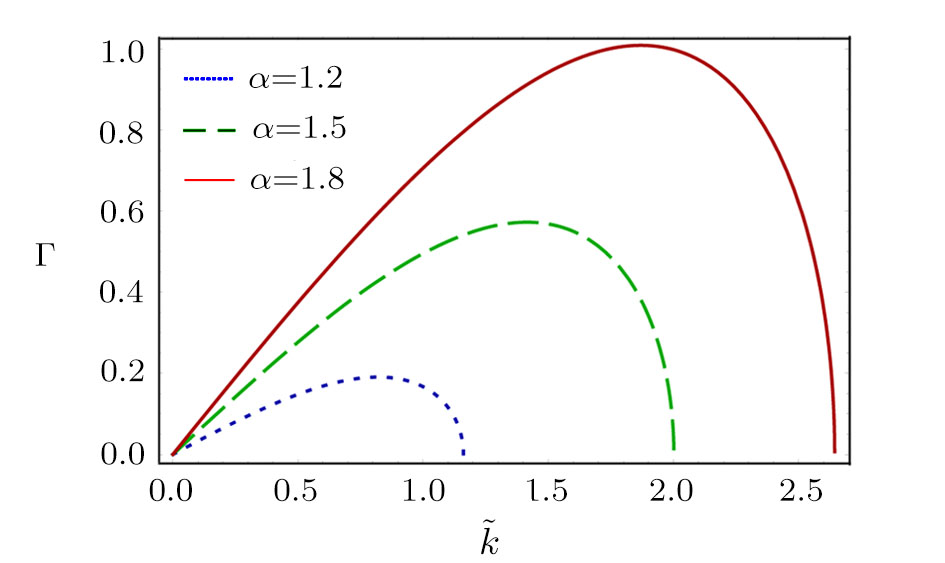 | Fig. 6 The variation of Γ with 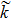
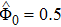
|
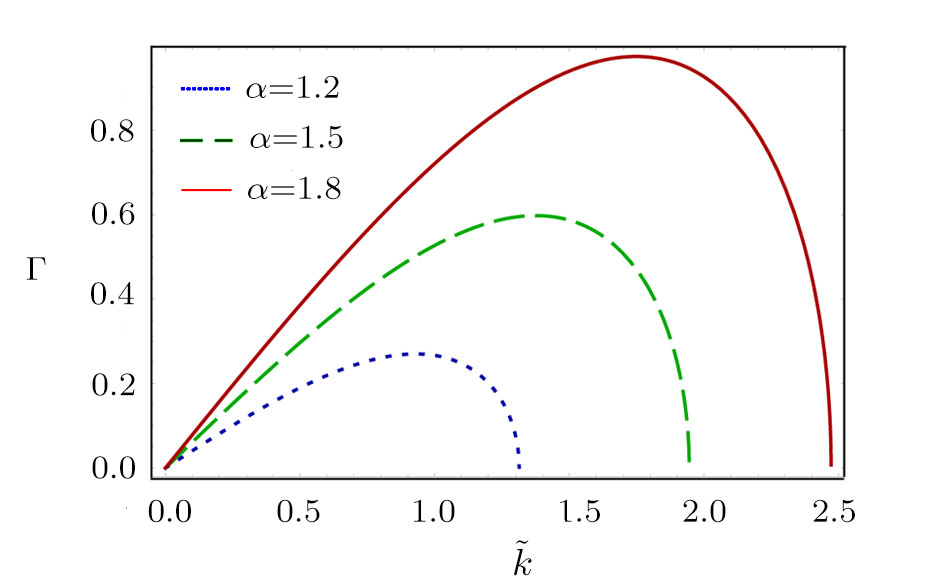 | Fig. 7 The variation of Γ with 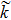
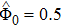
|
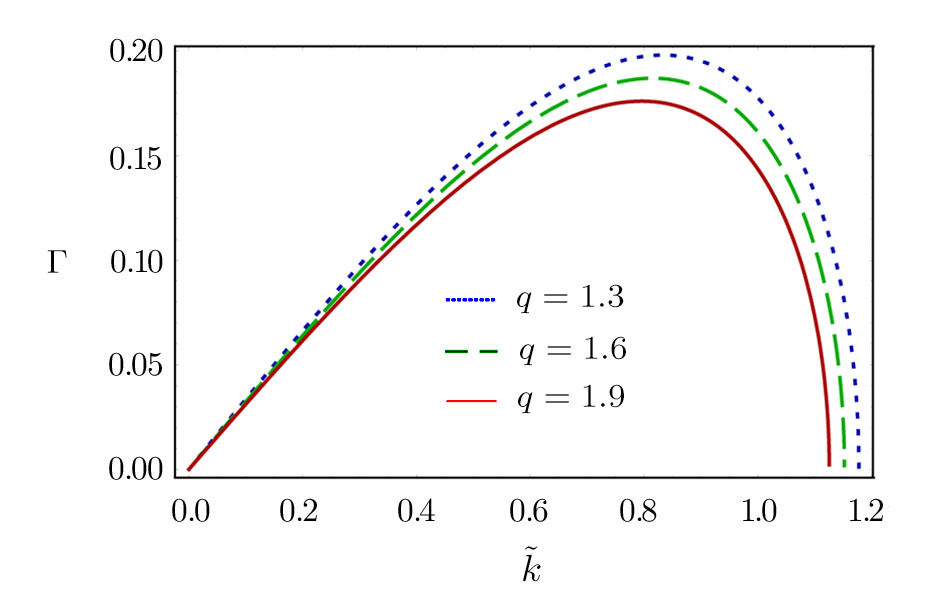 | Fig. 8 The variation of Γ with 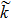
|
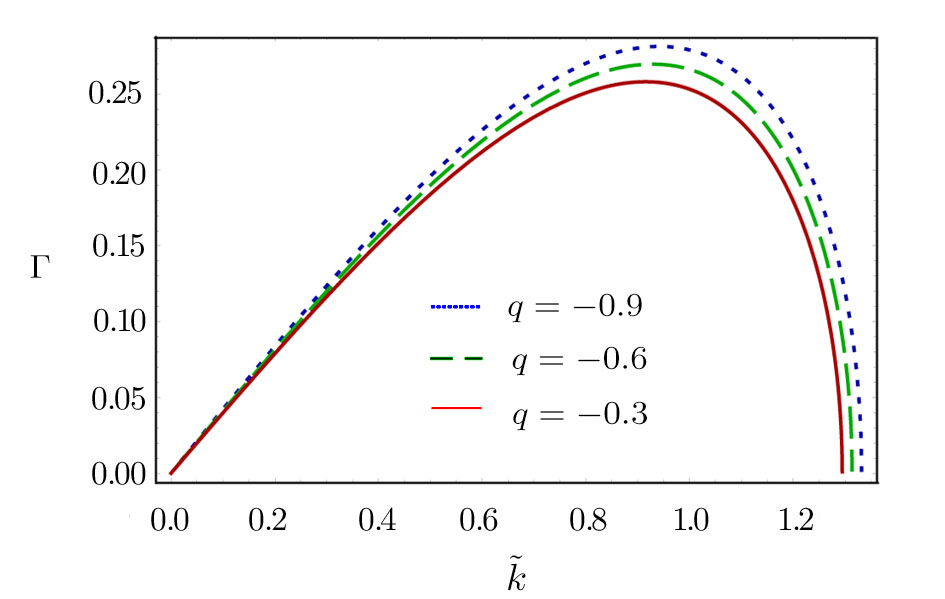 | Fig. 9 The variation of Γ with 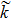
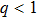
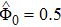
|
The effects of non-extensivity of the electrons on the MI growth rate can be observed from Figs. 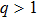
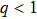
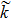
The bright (when 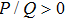
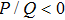
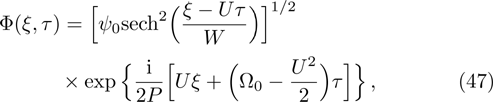
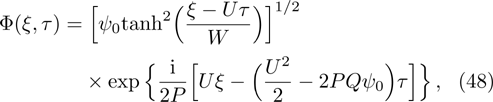
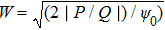
We have studied an unmagnetized realistic space dusty plasma system consists of q-distributed electrons, iso-thermal ions, positively charged warm dust grains as well as negatively charged warm dust grains. The RPM is used to derive the NLSE. The results that have been found from our investigation can be summarized as follows:
(i) The fast DA mode increases exponentially with z2 for fixed value of z1, n20, and n10 (via β). On the other hand, the slow DA mode linearly decreases with the increase of z2 for the fixed value of z1, n20, and n10 (via β).
(ii) The DAWs is modulationally stable (unstable) in the range of values of k in which the ratio P/Q is 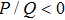
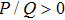
(iii) The value of kc increases with the increase of ni0 for fixed value of z1 and n10 (via μi and for fast mode). On the other hand, kc value decreases with the increase of m2 for fixed value of m1, z2, and z1 (via α and for slow mode).
(iv) The value of Γ increases with α for fixed value of q (within three ranges of q, namely, 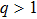
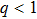
(v) The maximum value of Γ decreases (decreases) with the increase in the values of q for the limits 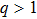
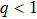
The results of our present investigation will be useful in understanding the nonlinear phenomena both in space (viz., Jupiters magnetosphere,[2] upper mesosphere, and comets tails,[2] etc.) and laboratory (viz., direct current and radio-frequency discharges, plasma processing reactors, fusion plasma devices,[1] and solid-fuel combustion products,[1] etc.) plasma system containing q-distributed electrons, iso-thermal ions, negatively and positively charged massive warm dust grains in OPDP medium.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] |