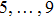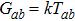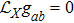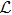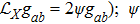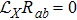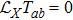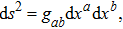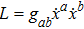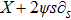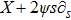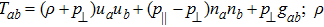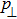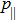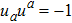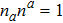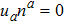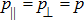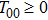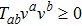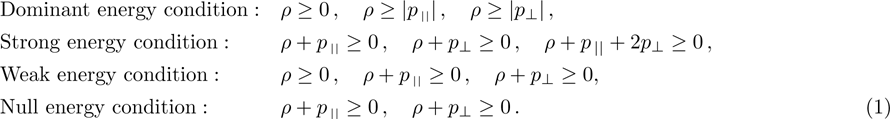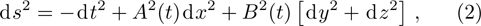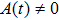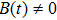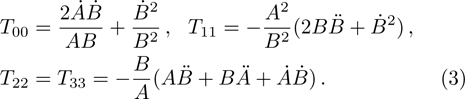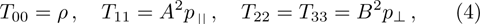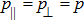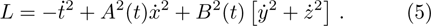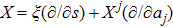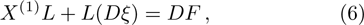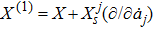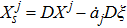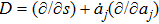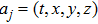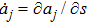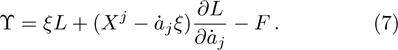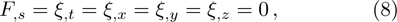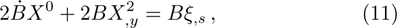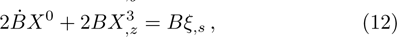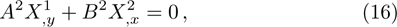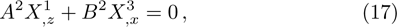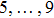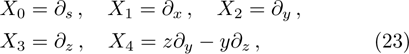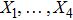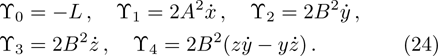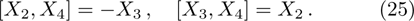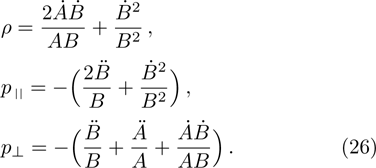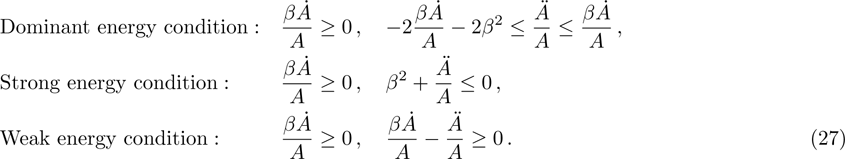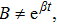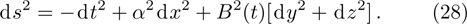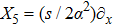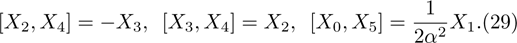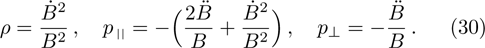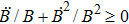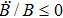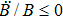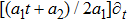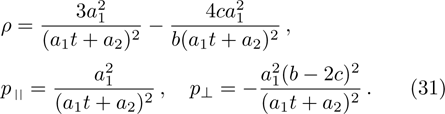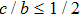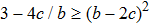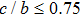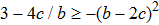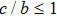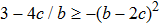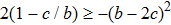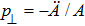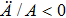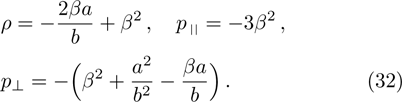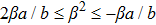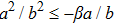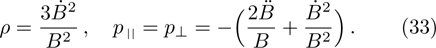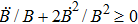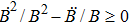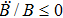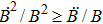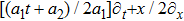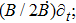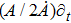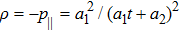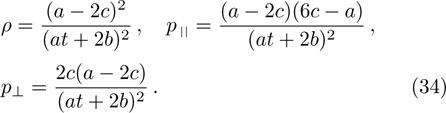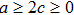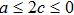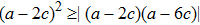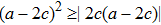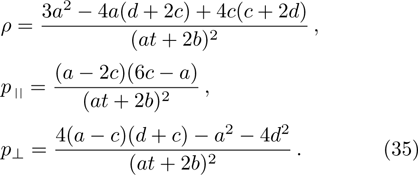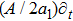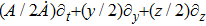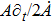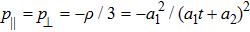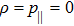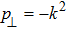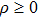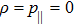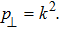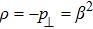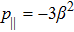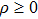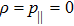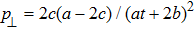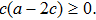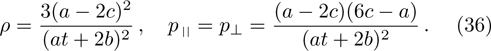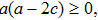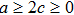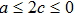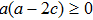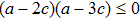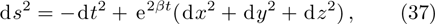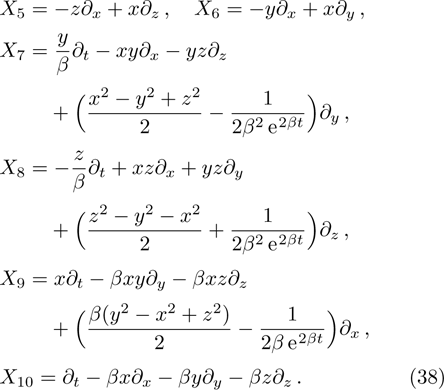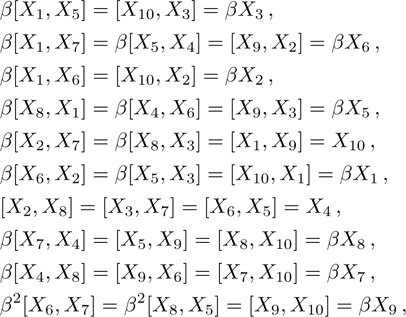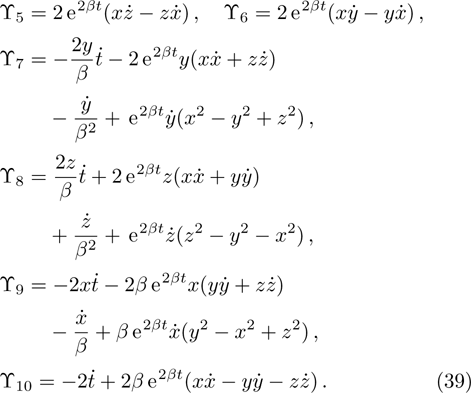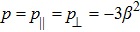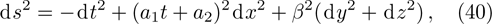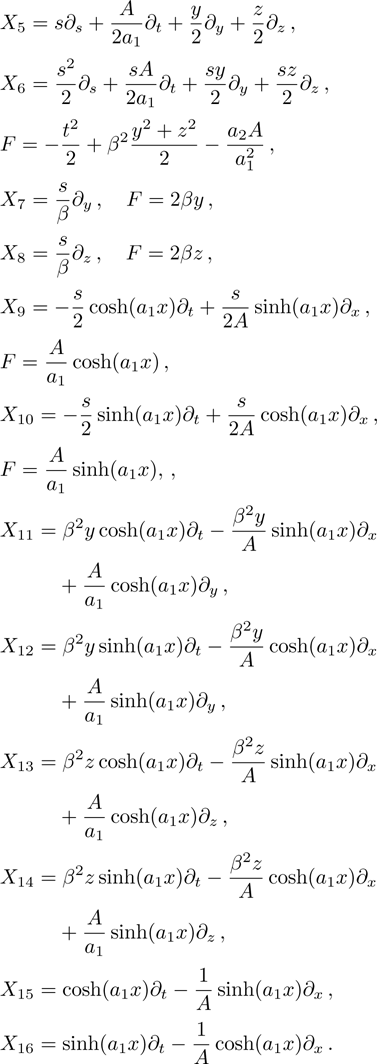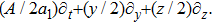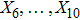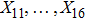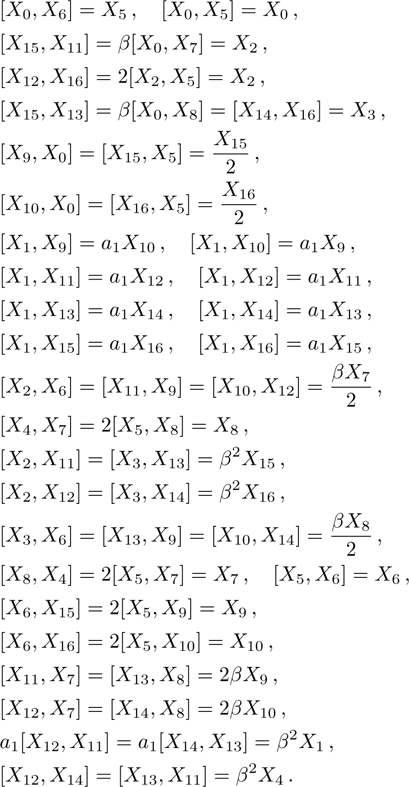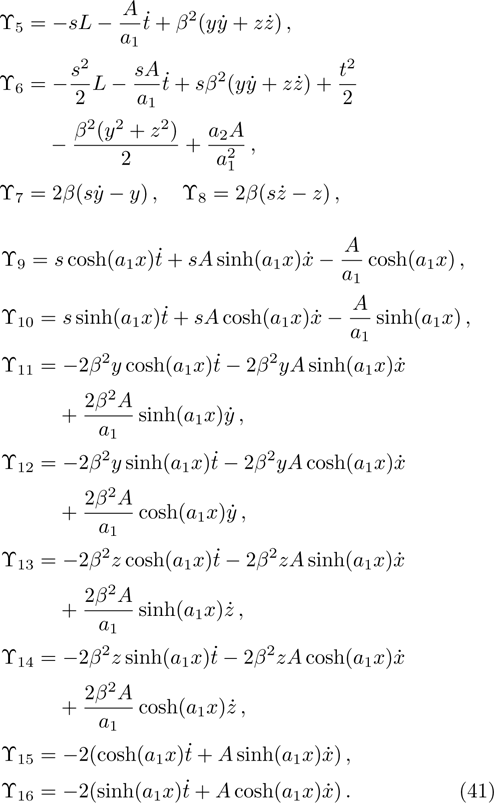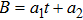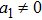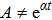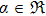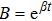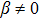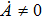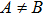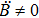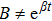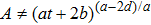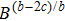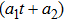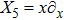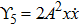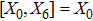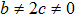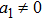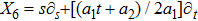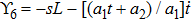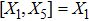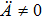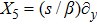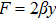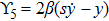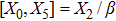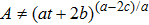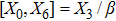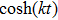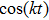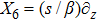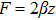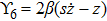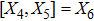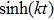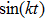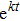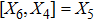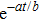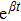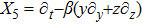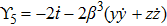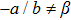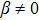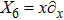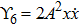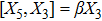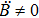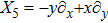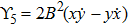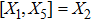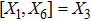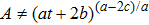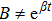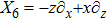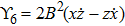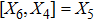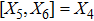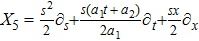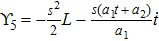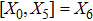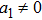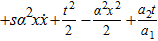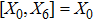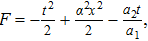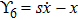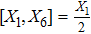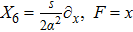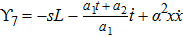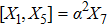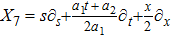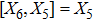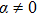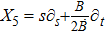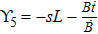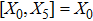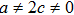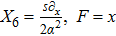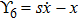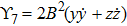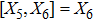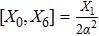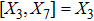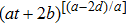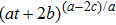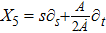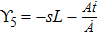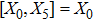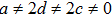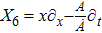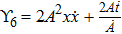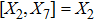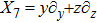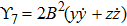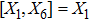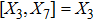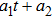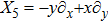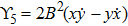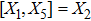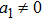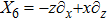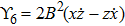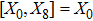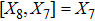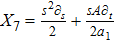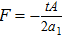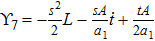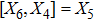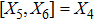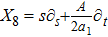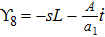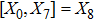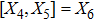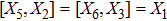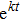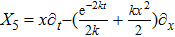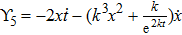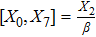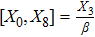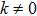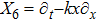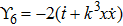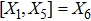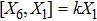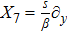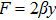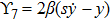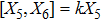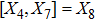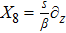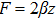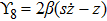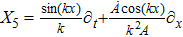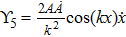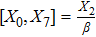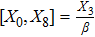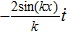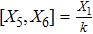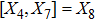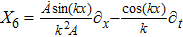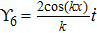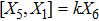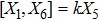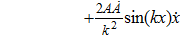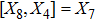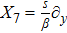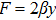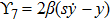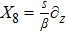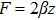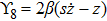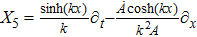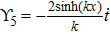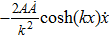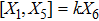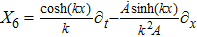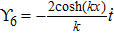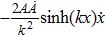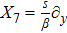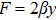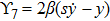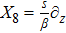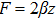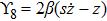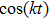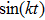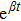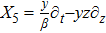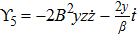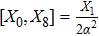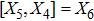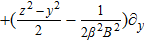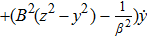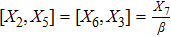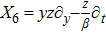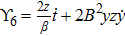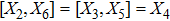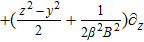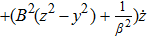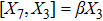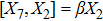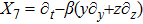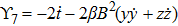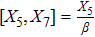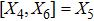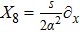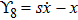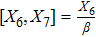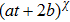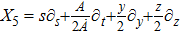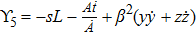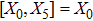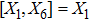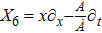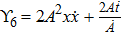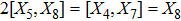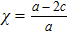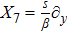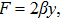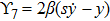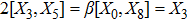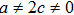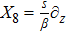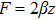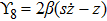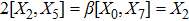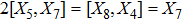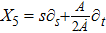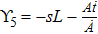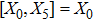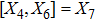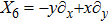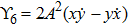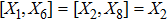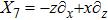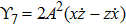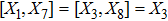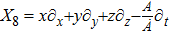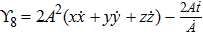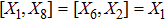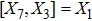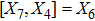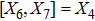The Einstein’s field equations (EFEs), 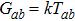, are ten tensor equations in the Einstein’s theory of general relativity, which relate the spacetime curvature with the energy and momentum within spacetime. The term G_ab appearing in these equations expresses the curvature of spacetime and is known as the Einstein tensor. Moreover, k signifies the gravitational constant and T_ab denotes the stress-energy tensor, which gives the description of density and flux of energy and momentum in the spacetime.

An exact solution of the EFEs is a Lorentz metric g_ab, which is obtained by solving these equations in closed form and is conformable to a physically realistic T_ab. The study of the exact solutions of these equations is proved to be one of the important activities in different branches of physics. They describe the structure of spacetime including the inertial motion of objects in the spacetime. Moreover, these solutions lead to the prediction of black holes and different models of evolution of universe. The problem which one faces in finding the exact solutions of these equations is their highly nonlinear nature. These equations cannot be solved without some simplifying assumption, such as symmetry restriction on g_ab. Using such restrictions, there are numerous cases where the EFEs are solved completely.^[1]

The most basic symmetry is expressed in terms of a Killing vector (KV) X satisfying the relation 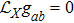, where 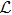denotes the Lie derivative operator and g_ab is the metric tensor. The KVs are closely related to the conservation laws in a spacetime. For a detailed study of exact solutions of EFEs with the help of symmetry restrictions on g_ab and the corresponding conservation laws, we refer to Refs. [1–3].

Some other conventional symmetries, which have been studied in the literature include homothetic vectors ( 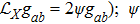being a constant, curvature collineations ( ), Ricci collineations ( 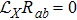) and matter collineations ( 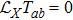). Recently, these collineations have been investigated for some physically important spacetimes.^[4–9]

In 1918, Emmy Noether^[10] proposed her work in terms of Noether theorem. As a result of this theorem, one can find the expression for conserved quantity for each continuous symmetry transformation that leaves the action invariant. NS are also called the variational symmetries and they are associated with mechanical systems possessing a Lagrangian. In particular, for a metric 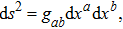the associated Lagrangian is given by 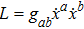. In this expression, a dot denotes differentiation with respect to the geodesics parameter s of the world line of a point particle moving in a spacetime. It is well known that every KV is an NS but there may exist some NS, which are not KVs. Thus the additional NS may yield some extra conservation laws. Homothetic vectors (HVs) are also closely related with NS. Corresponding to every homothetic vector X, we have an NS, 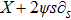. Conversely, if the vector field 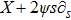is an NS, then X is an HV provided that X does not depend on s.^[11]

In literature, NS, their relation will Killing and homothetic vectors and the corresponding conservation laws have been studied by many researchers, for details we refer to Refs. [11–19].

The term T_ab appearing in EFEs is crucial as it describes the physics of a spacetime. The exact solutions of these equations may not give physically interesting results unless the source of T_ab is specified. For different sources, T_ab has some particular form. For example, for an anisotropic fluid, 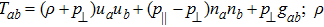, u_a and n_a being energy density, four-velocity and spacelike unit vector respectively. The quantities 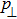and 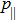respectively represent the perpendicular and parallel pressures to n_a. Moreover, 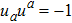, 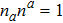and 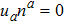.^[20] Similarly, for a perfect fluid we have the same form of T_ab with .

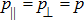The positive energy condition is a relation satisfied by the component T₀₀ of stress-energy tensor, which ensures that the energy density is non negative. The physical importance of this condition is evident from the fact that the empty vacuum may become unstable if both positive and negative energy regions are allowed.

There are some other energy conditions including weak, strong, null and dominant energy conditions, which generalize the condition 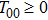to the whole tensor T_ab. The weak energy condition states that 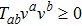, for any timelike vector v^a at a point of the spacetime manifold. For an anisotropic source, all the energy conditions take the form:

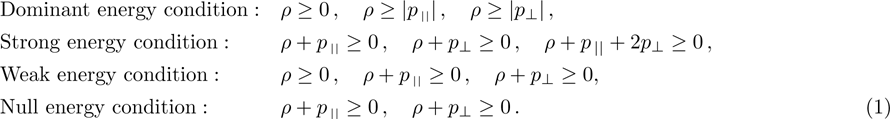
In particular, if 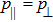, then these conditions reduce to the energy conditions for a perfect fluid.

According to the Bianchi classification of all the 3-dimensional real Lie algebras, there are nine types of Bianchi spatially homogeneous but not necessarily isotropic spacetimes. As a subclass, these models contain the isotropic Friedmann-Robertson-Walker (FRW) universes. The Bianchi type models are of vital importance because the physical variables in these models are dependent on time only. Consequently, the EFEs and other governing equations reduce to ordinary differential equations.

Among the Bianchi type models, the Bianchi type I spacetimes are those models for which the group G₃ of translations of the 3-dimensional Euclidian space is Abelian. In the literature, Bianchi type I spacetimes have been thoroughly studied from the symmetry point of view. Paliathanasis et al.^[21] presented the symmetry classification of the Klein-Gordon equation in Bianchi I spacetimes, which in turn related the Lie symmetries of this equation with the conformal Killing vectors (CKVs) of the underlying geometry. In the same analysis, it was also shown that the resulting Lie symmetries of the conformal algebra are also NS. Tsamparlis et al.^[22] studied the CKVs of Bianchi type I spacetimes and conjectured that there are only two conformally flat and two non conformally flat families of these spacetimes admitting CKVs. The same authors stated that for dynamical system whose equations of motion are of the form 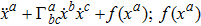being an arbitrary function of its argument, the computation of Lie and NS reduce to the probelm of finding the special projective collieations.^[23] These general results are then applied to the analytic computation of the Bianchi I metric.

In this paper, we present a complete classification of LRS Bianchi type I spacetimes via NS and the corresponding conservation laws. The bounds for energy conditions are also calculated for all the obtained models. In next section, we derive the list of determining equations for NS. In Secs. 3–9, we present different metrics, their Noether generators and corresponding conservation laws. For each of the obtained model in these sections, a brief discussion on the energy conditions is provided. A conclusion of the present work is appended at the end of the paper.

The metric of the LRS Bianchi type I spacetimes is given by:^[1]
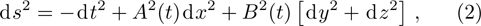
such that 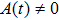and 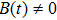. For this metric, the EFEs with k = 1 give:
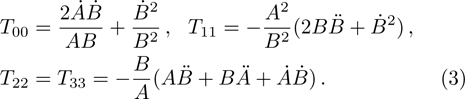
Here a dot on A and B denotes differentiation with respect to t. For an anisotropic fluid, these components become:
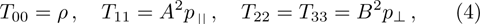
while for a perfect fluid, we have the same values of T_ab with 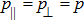. Following is the Lagrangian corresponding to the metric (2):
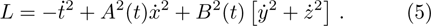
An NS vector field X is a vector field of the form 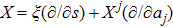, satisfying the following condition:
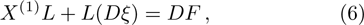
where 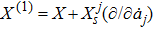is the first prolongation of X and 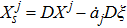with 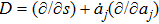. Moreover, ξ, X^j and the Gauge function F all depend on s and a_j, where 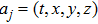are depending variables of s such that .

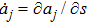Using the Noether’s theorem, the corresponding conservation law for each NS can be found with the help of the expression:
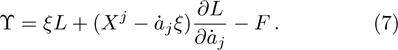
We may simplify Eq. (6) by using the Lagrangian (5) to get the following set of determining equations:














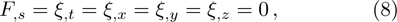
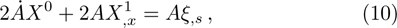
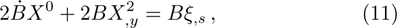
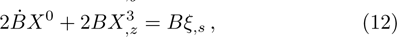
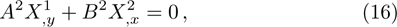
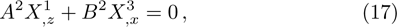
The components X^a of the NS vector field, the Gauge function F and the metric functions A and B appearing in the above system can be found by decoupling and then integrating these equations systematically. In this way, we may get the exact form of LRS Bianchi type I metrics along with their NS. During this procedure, several cases arise which restrict A and B to satisfy certain conditions and give the exact form of LRS Bianchi type I metric admitting NS having dimension 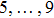, 11, and 17. To avoid the repetition, we exclude to write the basic calculations and present the metrics along with their NS, conservation laws, Lie algebra and some physical implications in the upcoming sections.

The minimal set of NS admitted by LRS Bianchi Type I metric is found to be:
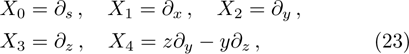
where X₀ is the symmetry corresponding to the Lagrangian and 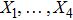are the minimum KVs of the metric (2). The above minimal set of NS is obtained under the following restrictions on metric functions. 1

Table 1.

Table 1.

Table 1. Metrics admitting 5 NS . No. A(t) B(t) 5a for all , 5b for all , 5c , , and

Table 1. Metrics admitting 5 NS .

Using Eq. (7), the conservation laws for the above set of minimal NS are obtained as:
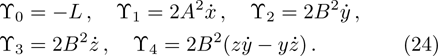
The corresponding Lie algebra for the generators given in Eq. (23) is:
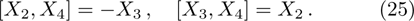
The metrics 5a–5c are anisotropic fluids for which:
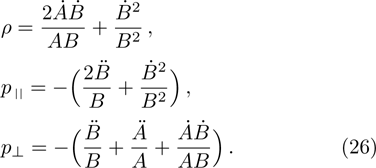
One may use these values in Eq. (1) to find the energy bounds for the metrics 5a-5c. For example, for the metric 5b, the energy conditions restrict the metric function A as follows:

If A=α, where α is a non zero constant and B satisfies the conditions and then the metric (2) becomes:
For this metric, we obtain six NS, out of which five are same as given in Eq. (23) and the sixth one is a proper NS, , with the Gauge function F = x. The corresponding invariant for this Noether generator is and the Lie algebra of these six NS generators is given by:
For the metric (28), being an anisotropic fluid, the physical terms are found to be:
Here the dominant energy condition holds if and and the remaining energy conditions are satisfied provided that .

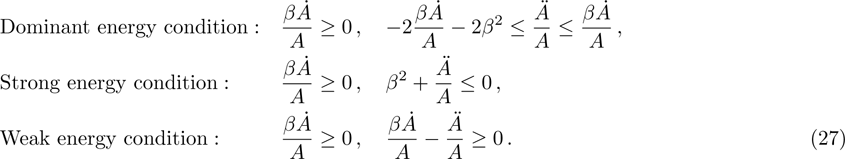
In Table 2, we present some LRS Bianchi type I metrics each of which admits a 7-dimensional Lie algebra of NS. For each of these metrics, five NS are same as given in Eq. (23), while the extra two NS along with their conservation laws and Lie algebra are listed with each metric.

Table 2.

Table 2.

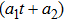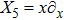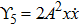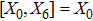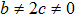
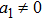
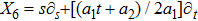
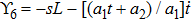
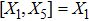
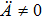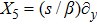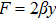
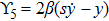
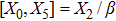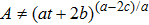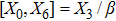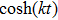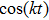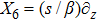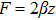
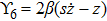
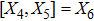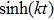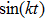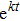
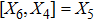
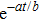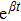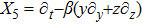
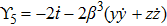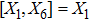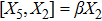
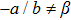
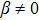
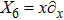
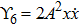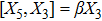
Table 2. Metrics admitting 7 NS. . No. A(t) B(t) NS Invariants Lie algebra 7a , , , , , 7b such that B=β , , , , , , , , , and 7c , , , , , 7d A = B , , , ,

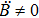
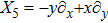
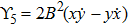
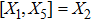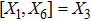
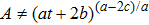
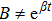
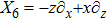
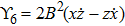
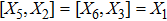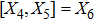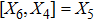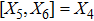
Table 2. Metrics admitting 7 NS. .

For the metric 7a, X₅ is a KV and X₆ corresponds to a homothetic vector 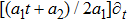with the homothetic constant 1/2. In case 7b, both X₅ and X₆ represent proper NS. Finally, both X₅ and X₆ are KVs for the metrics 7c and 7d.

The metric in case 7a is an anisotropic fluid with:
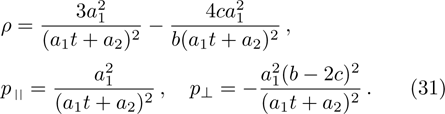
The above expressions satisfy the dominant energy conditions if 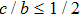and 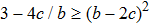, while the weak energy conditions hold if 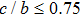and 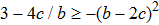. Moreover, the strong energy conditions are satisfied when 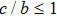, , 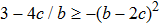and .

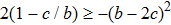Similarly, the metric in case 7b is an anisotropic fluid whose energy density and parallel pressure vanish and 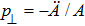. Here the dominant energy condition is clearly failed, while the remaining energy conditions are satisfied provided that .

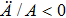The energy momentum tensor components for the model 7c, being an anisotropic fluid, produces the following expressions:
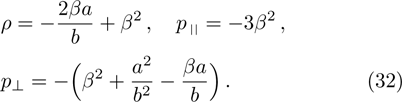
For the above values, the strong and dominant energy conditions are failed, while the weak energy conditions hold when 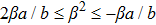and .

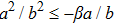Finally, for the metric 7d we have:
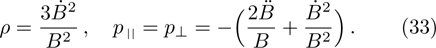
Here we have obtained a perfect fluid matter such that the dominant energy conditions hold if 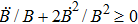and 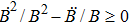, while strong and weak energy conditions respectively require 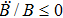and .

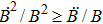In Table 3, we give all the LRS Bianchi type I metrics admitting eight NS, out of which five are same as given in Eq. (23).

Table 3.

Table 3.

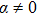
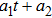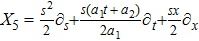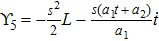
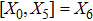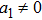
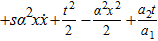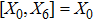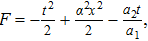
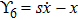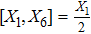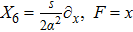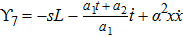
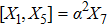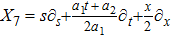
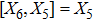
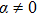
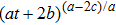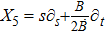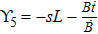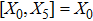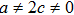
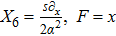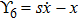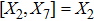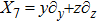
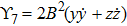
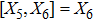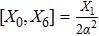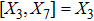
Table 3. Metrics admitting 8 NS. . No. A(t) B(t) NS Invariants Lie algebra 8a , , , , , , , , , 8b , , , , , , , , , 8c , , , , , , , ,

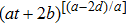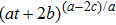
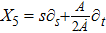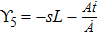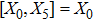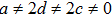
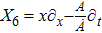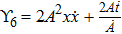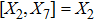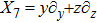
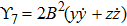
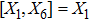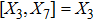
Table 3. Metrics admitting 8 NS. .

For metric 8a, X₅ and X₆ are proper NS, while X₇ corresponds to an HV 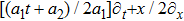. In case of metric 8b, X₅ corresponds to an HV 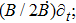X₆ is a proper NS while X₇ is a KV. Finally for case 8c, X₅ is an NS corresponding to the HV 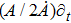and X₆, X₇ are KVs.

The metric 8a represents an anisotropic fluid with zero perpendicular pressure and 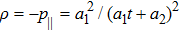. All the energy conditions are satisfied here. Similarly, The metric 8b is also an anisotropic fluid for which we have:
such that the strong and weak energy conditions hold if either or , while for dominant energy condition we must have and 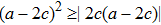. The physical terms for case 8c are given by:
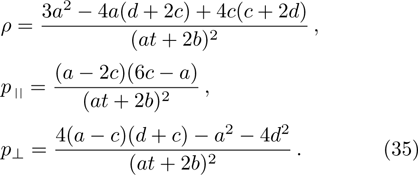
One may simplify the energy conditions using the above values, like the previous cases.

There are nine metrics each of which possesses 9-dimensional algebra of NS. All such metrics and the four additional NS different from those given in Eq. (23) for each of these metrics along with their conservation laws and Lie algebra are presented in Table 4.

Table 4.

Table 4.

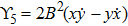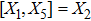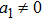
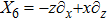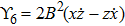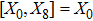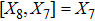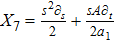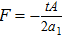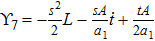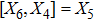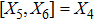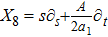
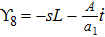
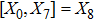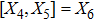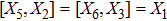
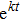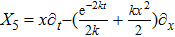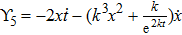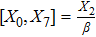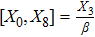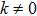
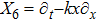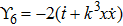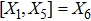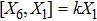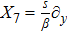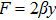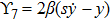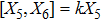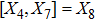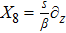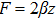
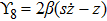
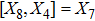
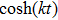
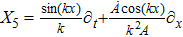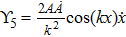
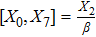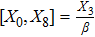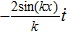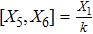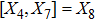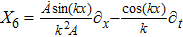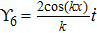
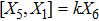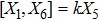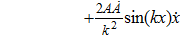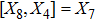
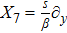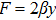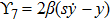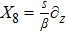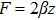
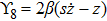
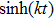
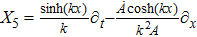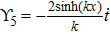
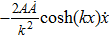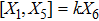
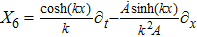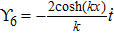
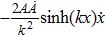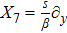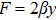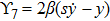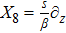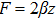
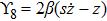
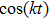
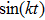
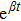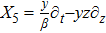
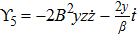
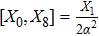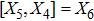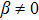
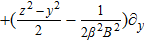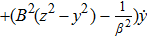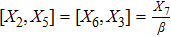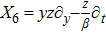
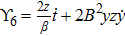
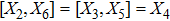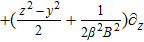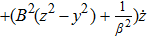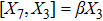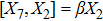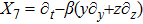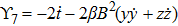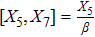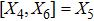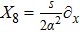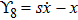
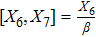
Table 4. Metrics admitting 9 NS. . No. 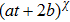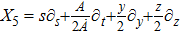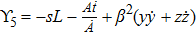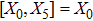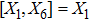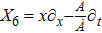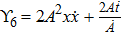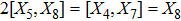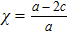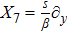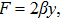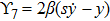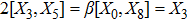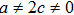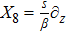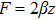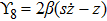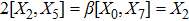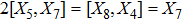A(t) B(t) NS Invariants Lie algebra 9a , B = A , , , , , , , , , , , , , , , 9b , β , , , , , , , , , , , , , , 9c β , , , , , , , , , , , , , , 9d β , Same as case 9c except , , , , , , , 9e β Similar to 9d Similar to 9d Same as case 9c 9f β Similar to 9d Similar to 9d Same as case 9d 9g α , , , , , , , , , , , , , , , , F = x 9h , β , , , , , , , , , , , , , , 9i as in 9h B = A, , , , , , , , , , , , , ,

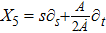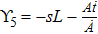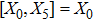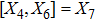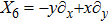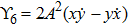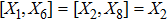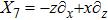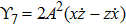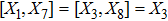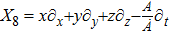
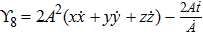
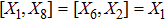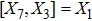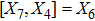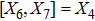
Table 4. Metrics admitting 9 NS. .

For the metric 9a, X₅ and X₆ represent KVs, X₇ is a proper NS while X₈ is an NS corresponding to an HV 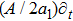. In cases 9b–9f, X₅ and X₆ are KVs, while X₇ and X₈ are proper NS. The metric given in case 9g admits three additional KVs X₅, X₆, and X₇ along with a proper Noether symmetry X₈. For the metric 9h, X₅ is an NS which corresponds to an HV 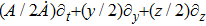, X₆ is a KV while X₇ and X₈ are proper NS. Finally, in case 9i, we have three additional KVs X₆, X₇, X₈, and one NS X₅ corresponding to the HV .

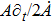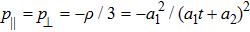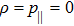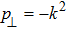The metric 9a represents a perfect fluid, while all the remaining cases give anisotropic fluids. For the metric 9a, we find , which satisfy all the energy conditions. For the models in cases 9b–9d, we get and , which do not satisfy any energy condition except the positive energy condition, 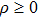. Similarly, for models 9e and 9f, we have 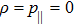and 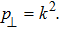Here the dominant energy condition fails, while all the remaining energy conditions are trivially satisfied. 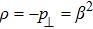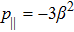For the model 9g, we obtain and , which do not satisfy any energy condition except 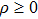. The metric given in 9h is an anisotropic fluid for which 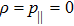and 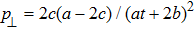. The dominant energy condition is clearly failed, while the remaining energy conditions are satisfied provided that 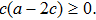The following physical terms for the metric 9i reveal that it represents a perfect fluid model:
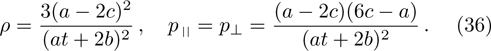
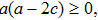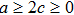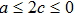The corresponding weak energy conditions hold for whereas the strong energy conditions require or . Moreover, the dominant energy conditions are satisfied if 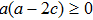, and .

Following is the only one metric which admits eleven NS:
where The set of eleven NS for the above metric contains the minimal set of NS and the extra six NS (KVs) are obtained as:

The Lie algebra for the above set of generators is found to be:
and the corresponding conservation laws are:
For the metric (37), we have and . Thus it gives a perfect fluid. Here the strong energy condition is violated while the remaining energy conditions are satisfied.

It is well known that the the dimension of Noether algebra for flat Minkowski metric is 17. Following is an another metric admitting 17 NS.
where and Five NS of the above metric are same as given in Eq. (23), while the remaining twelve are given as follows:
In the above set, X₅ is an NS and its corresponding HV is Moreover, are proper NS and are KVs. The Lie algebra for these generators is given by:

In this case, the conservation laws are obtained as:
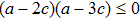For the metric (40), we have T_ab=0. Thus it represents a vacuum solution.

In this paper, we have studied the NS of LRS Bianchi type I spacetimes. For a complete classification, the Noether determining equations are generally solved, which in result categorized the mentioned spacetimes metric into seven different classes according to the dimension of Noether algebra. The possible dimension of Lie algebra of Noether symmetry turned out to be 5, 6, 7, 8, 9, 11, and 17. These NS are compared with Killing and homothetic vectors and it is shown that the possible dimension of Killing algebra for LRS Bianchi type I spacetime is 4, 5, 6, 7 or 10. Besides this, the conservations laws are presented for all the Noether symmetry generators by using the well known Noether’s theorem. Finally, it is observed that most of the obtained metrics are anisotropic or perfect fluids satisfying different energy conditions.

We are thankful to the referees for their useful suggestions on the manuscript.