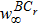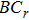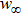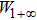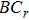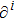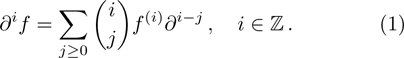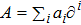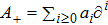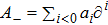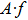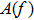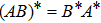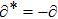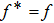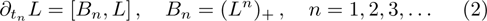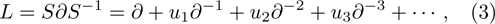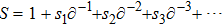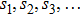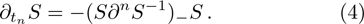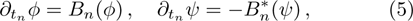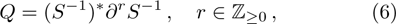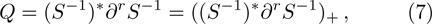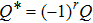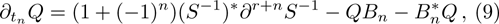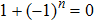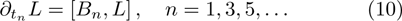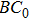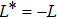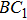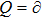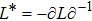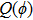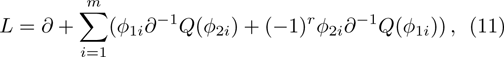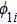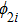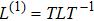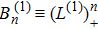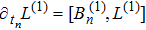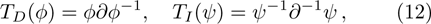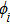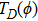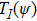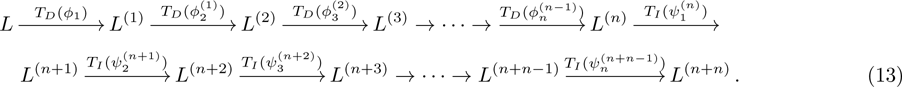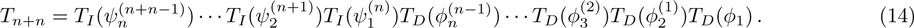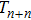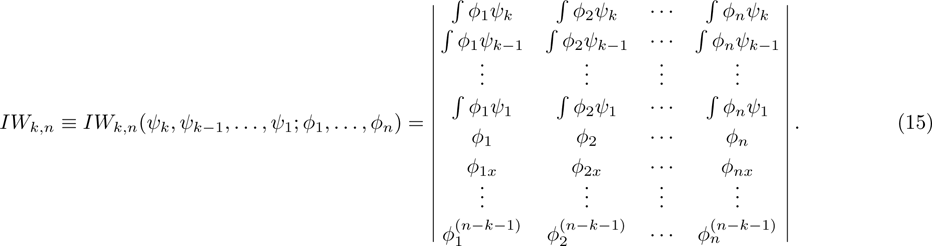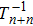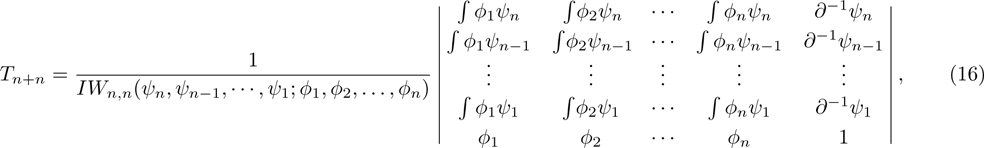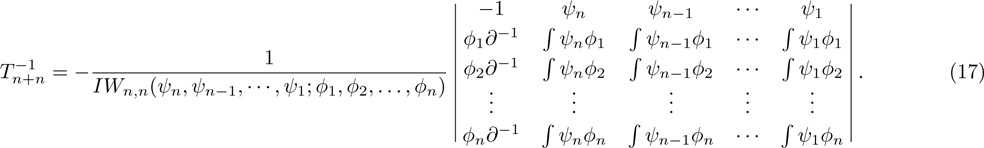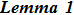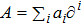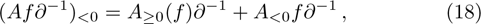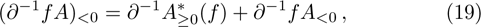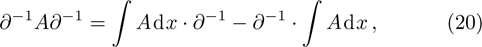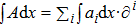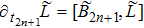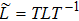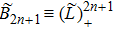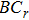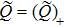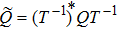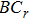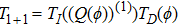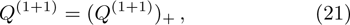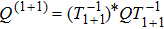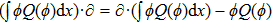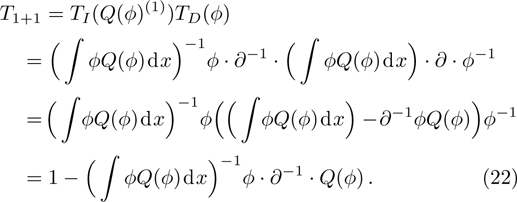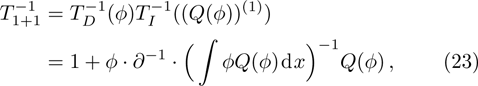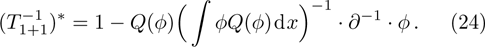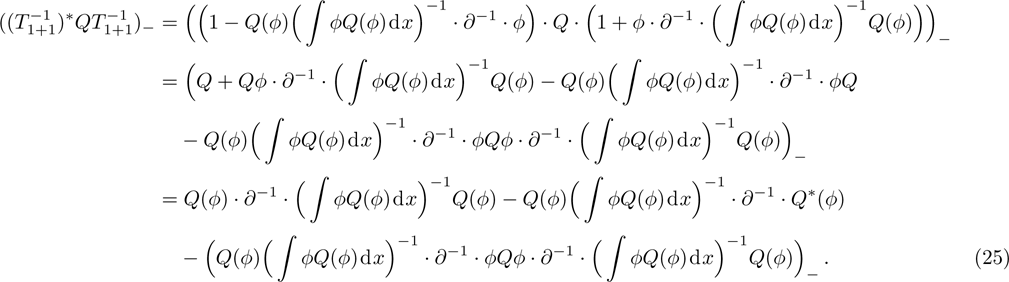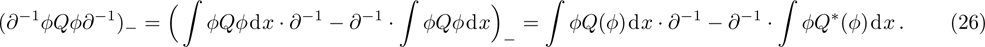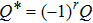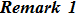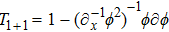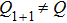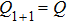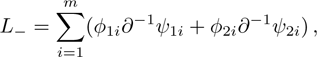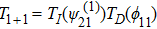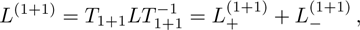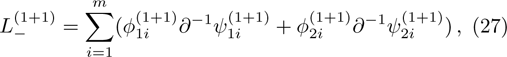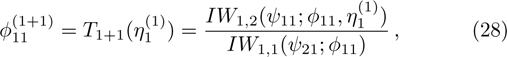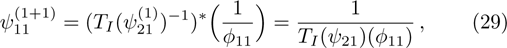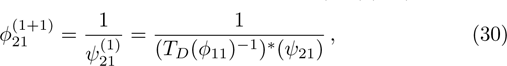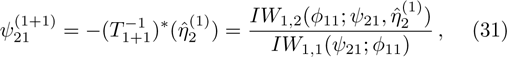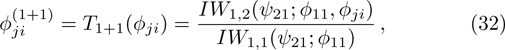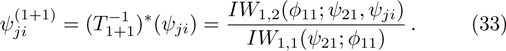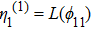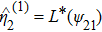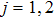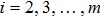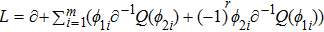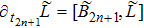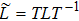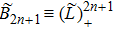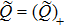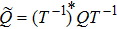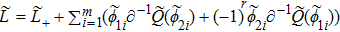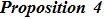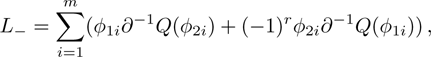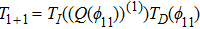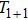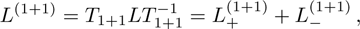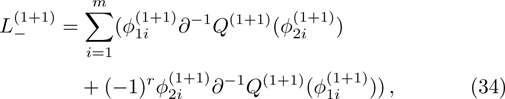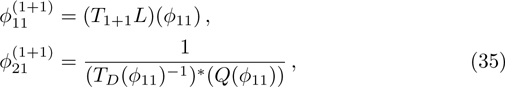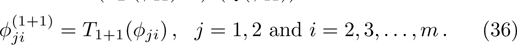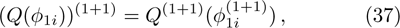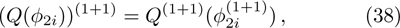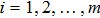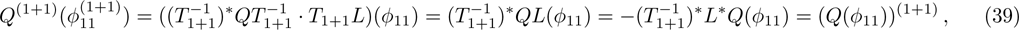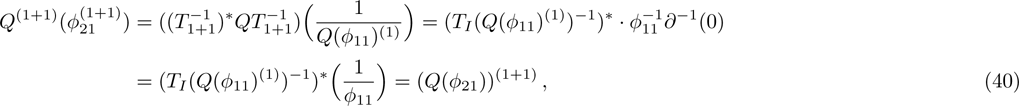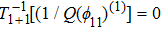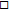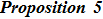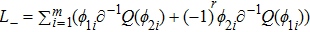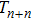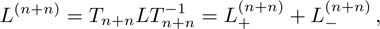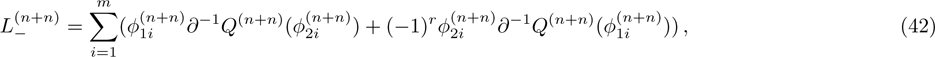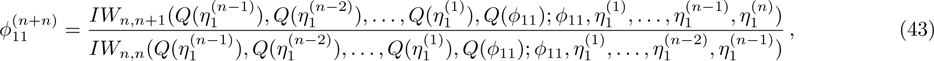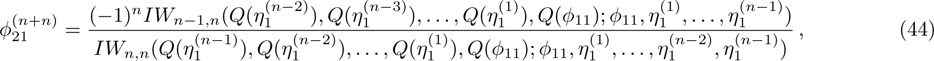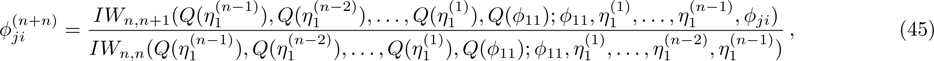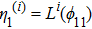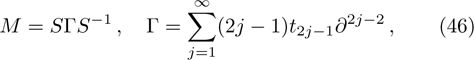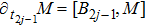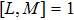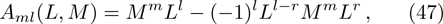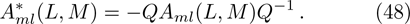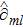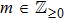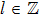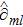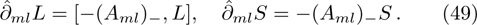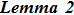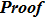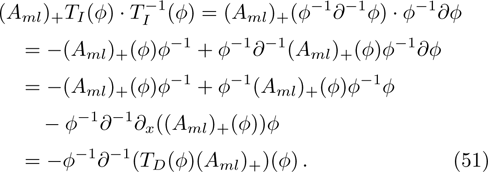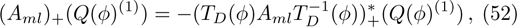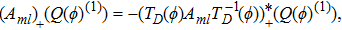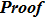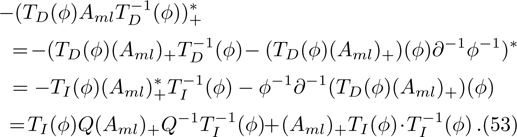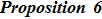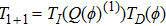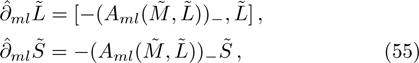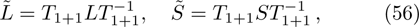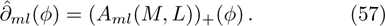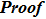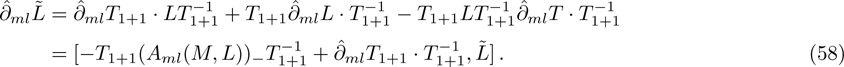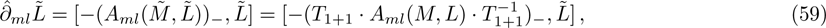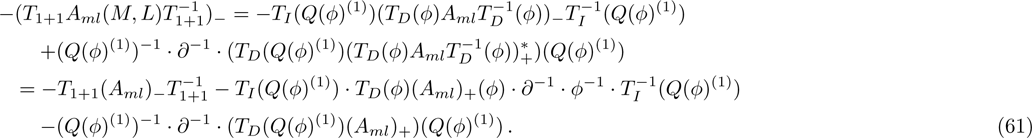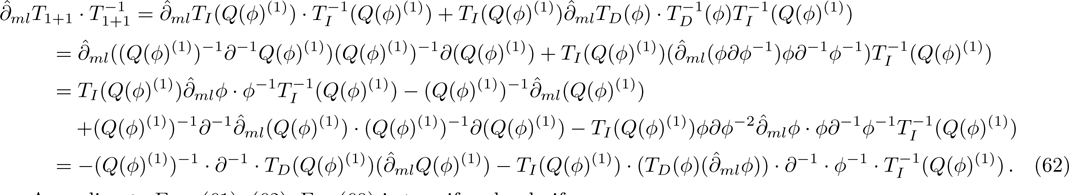Cite this Article
Geng Lu-Min, Chen Hui-Zhan, Li Na, Cheng Ji-Peng. Gauge Transformation for BCr-KP Hierarchy and Its Compatibility with Additional Symmetry. Communications in Theoretical Physics, 2019, 71(3): 274  
Permissions
Gauge Transformation for BCr-KP Hierarchy and Its Compatibility with Additional Symmetry
Geng Lu-Min, Chen Hui-Zhan, Li Na, Cheng Ji-Peng
School of Mathematics, China University of Mining and Technology, Xuzhou 221116, China

 

† Corresponding author. E-mail: chengjp@cumt.edu.cn

Abstract
Abstract

The BC-KP hierarchy is an important sub-hierarchy of the KP hierarchy. In this paper, the BCr-KP hierarchy is investigated from three aspects. Firstly, we study the gauge transformation for the BCr-KP hierarchy. Different from the KP hierarchy, the gauge transformation must keep the constraint of the BCr-KP hierarchy. Secondly, we study the gauge transformation for the constrained BCr-KP hierarchy. In this case, the constraints of the Lax operator must be invariant under the gauge transformation. At last, the compatibility between the additional symmetry and the gauge transformation for the BCr-KP hierarchy is explored.

Keyword:the BCr-KP hierarchy;gauge transformation;additional symmetry
1. Introduction

The Kadomtsev-Petviashvili (KP in short) hierarchy[1–2] is an important research area in the integrable systems. There is a kind of sub-hierarchy of the KP hierarchy studied by Date et al. in Ref. [3], which can be viewed as the generalization of the BKP and CKP hierarchies.[1,3–5] In Ref. [4], Zuo et al. made a slight modification for the sub-KP hierarchy of Ref. [3], and called it the BCr-KP hierarchy, to ensure its consistence with the CKP and BKP hierarchy in the case of r = 0 and r = 1 respectively. In Ref. [4], Zuo et al. not only constructed the additional symmetries of the BCr-KP hierarchy and its constrained case, but also showed that the corresponding additional symmetries form a 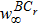-algebra and a Witt algebra respectively. In this paper, we will consider the gauge transformations and its relation with the additional symmetry of the BCr-KP hierarchy.

The gauge transformation[6–8] is an efficient way to construct solutions for integrable hierarchies. Its initial ideal dates back to the gauge equivalence with the different integrable models. The gauge transformation operators of the KP hierarchy[6–7] mainly included the differential type TD and the integral type TI. Now, the gauge transformations of many important integrable hierarchies have been constructed. For instance, the KP and modified KP hierarchies,[6–11] the BKP and CKP hierarchies,[12–14] the q-KP and modified q-KP hierarchies,[15–18] the discrete KP and modified discrete KP hierarchies.[19–21] In this paper, we focus on the gauge transformation operators of the BCr-KP hierarchy and its constrained case. Different from the KP hierarchy, the gauge transformations of the BCr-KP hierarchy must keep the 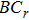-constraint invariant, besides keeping the Lax equation. It is found in this paper that the combination of TD and TI is the suitable choice of the gauge transformation for the BCr-KP hierarchy. As for the constrained case, the corresponding gauge transformations have to ensure the constrained form of the Lax operator unchanged, besides the two conditions in unconstrained case. In fact, this can be done, by choosing the eigenfunction in the negative part of the Lax operator as the generating function in the gauge transformation operators. What is more, the successive applications of the corresponding gauge transformation operators are considered in this paper.

Another topic in this paper is the additional symmetry.[1–2,22–24] The additional symmetries are from the 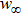algebra[24] or the so-called centerless 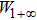-algebra, which are an exceptional kind of symmetries relying explicitly on the space and time variables.[25–28] Nowdays, there are many important results on the additional symmetries.[4,29–35] In this paper, we will study the compatibility of the additional symmetries and the gauge transformation for the BCr-KP hierarchy. It is an interesting question to discuss the changes of the additional symmetries under the gauge transformations. For the BCr-KP hierarchy after the gauge transformation, we find that the additional symmetries remain the ones, which shows some compatibilities of the additional symmetry and the gauge transformation.

The organization of this paper is as follows. In Sec. 2, some backgrounds of the BCr-KP hierarchy are introduced. In Sec. 3, the gauge transformations for the BCr-KP hierarchy are given to keep the 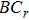-constraint. In Sec. 4, the gauge transformation for the constrained BCr-KP hierarchy on the Lax operator are investigated. In Sec. 5, we focus on the compatibility of the gauge transformations and the additional symmetries.

2. Background on the BCr-KP Hierarchy

In this section, we will review the backgrounds on the BCr-KP hierarchy,[4] based upon the pseudo-differental operators. The multiplication of 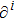with the f obeys the Leibnitz rule[2]
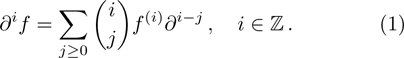
For 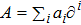, we denote 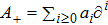and 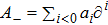. What is more, Af or 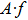means that the multiplication of A and f, while 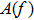denotes the action of A on f. The conjugate operation * obeys the following rules: 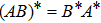, , 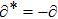, 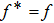for any pseudo-differential operators A and B and any function f.

Let us introduce the KP hierarchy[1–2] firstly, since BC r-KP hierarchy is a kind of sub-hierarchy of the KP hierarchy. The Lax equation of the KP hierarchy is defined by
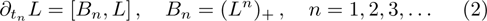
Here the Lax operator is given by
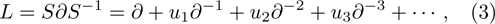
and 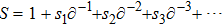is called the dressing operator. And the coefficients 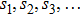are the functions of infinitely many variables 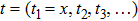. The Lax equation (2) is equivalent to the Satoʼs equation:
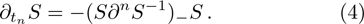
The eigenfunction ϕ and the adjoint eigenfunction ψ of the KP hierarchy are defined by
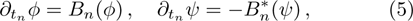
respectively.

Next introduce
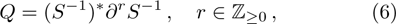
where S is the dressing operator of the KP hierarchy. Generally, the BCr-KP hierarchy[3–4] can be defined by imposing the condition below on the dressing operator S,
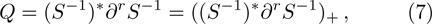
which means that Q is an r-order differential operator satisfying 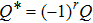. Further according to Eqs. (3) and (4), one can find

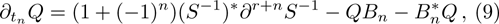
and by talking the negative part and using Q=Q +, one gets 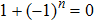. Therefore, the BCr-KP hierarchy only has odd flows.

By summarizing the results above, the BCr-KP hierarchy is defined by
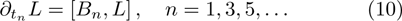
and the Lax operator L in Eq. (3) has the reduction condition (7) or (8). Notice that

(i) 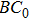-KP is the CKP hierarchy. When r = 0, one can find Q = 1 and .

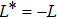(ii) 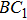-KP is the BKP hierarchy. When r = 1, one can fi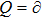nd and .

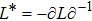According to Eqs. (5) and (8), it can be found that the adjoint eigenfunction of the BCr-KP hierarchy can be expressed by 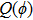, where ϕ is an eigenfunction. The constrained BCr-KP hierarchy[4] is defined by imposing the below constraints on the Lax operator of BCr-KP hierarchy
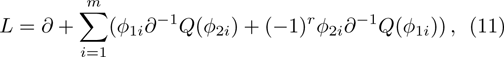
where 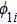and 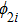are two eigenfunctions of the BCr-KP hierarchy.

3. The Gauge Transformation for the BCr-KP Hierarchy

In this section, we will consider the gauge transformation of the BCr-KP hierarchy.

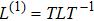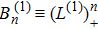Firstly, let us review the gauge transformation of the KP hierarchy.[6–7] Assume that T is a pseudo-differential operator and L is the Lax operator of the KP hierarchy. Denote and . If 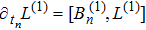still holds, then T is called the gauge transformation operator for the KP hierarchy. There are two elementary types of the gauge transformation operator in the KP case.
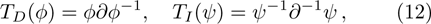
where ϕ and ψ are the eigenfunction and adjoint eigenfunction respectively.

Given eigenfunction 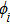and adjoint eigenfunction 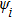for 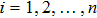, consider the following chain of the gauge transformation operators 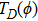and .
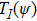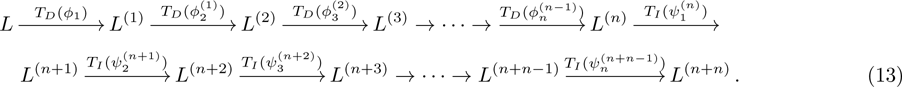
Denote
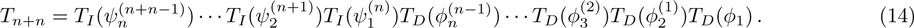
The next proposition will give the explicit form of 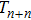. For this, the generalized Wronskian determinant[9] will be needed, which is defined by

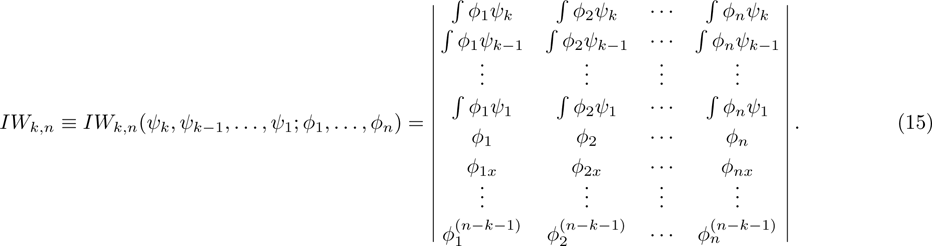
[9] and have the following forms

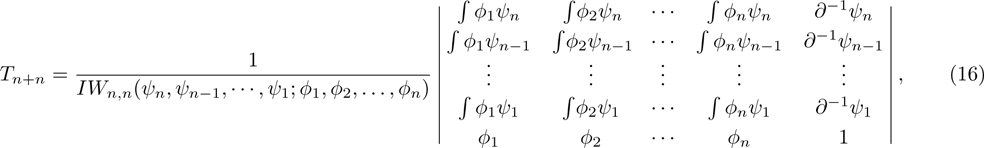
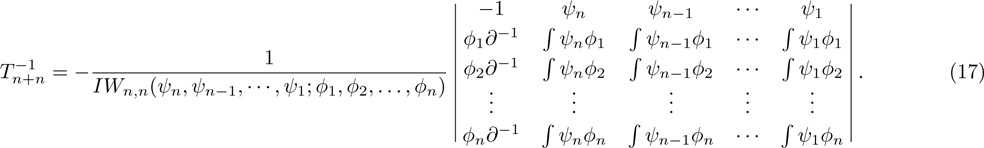
Before further discussing, the next lemma will be needed.

[7,11] For any functions f and any pseudo differential operator ,


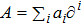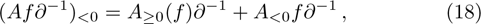
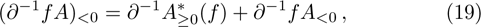
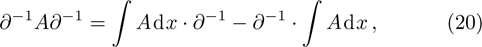
where .

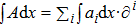After the above preparation, we begin to consider the gauge transformations of the BCr-KP hierarchy. The gauge transformation operator T of the BCr-KP hierarchy must satisfy the following two conditions, which are different from the KP hierarchy, that is

(i) Keeping the Lax equation: 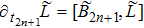, where 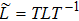and .

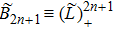(ii) Keeping the 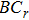-constraint: 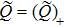, where .

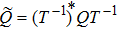However in the BCr-KP hierarchy, single TD or TI can not ensure the 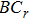-constraint invariant. Fortunately, it is found that the combination of TD and TI, i.e., 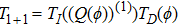, can satisfy the two conditions above. We will show this fact below.
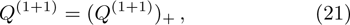
with .

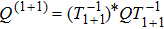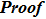Firstly by using ,
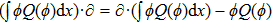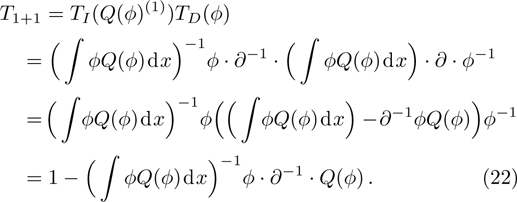
Similarly
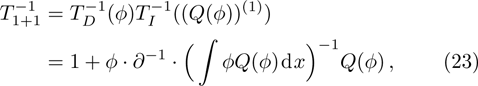
therefore

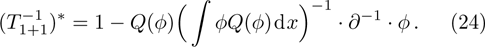
Then according to Eqs. (22), (24) and Lemma 1,
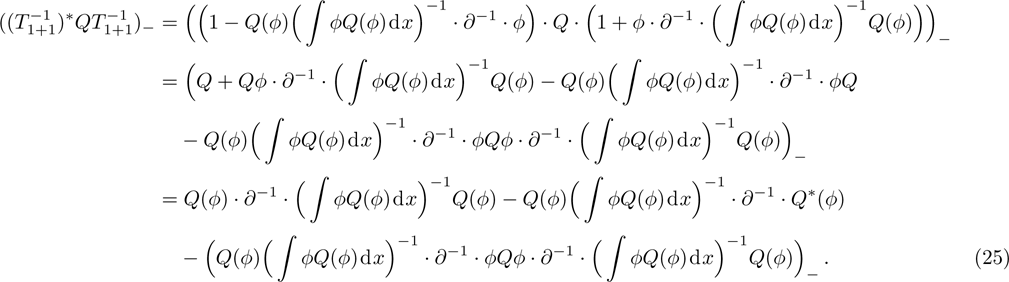
Further according to Lemma 1

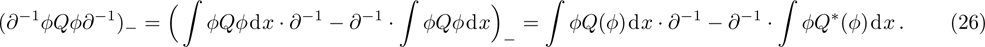
By subsituting Eq. (26) into Eq. (25) and using the relation 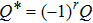, one can at last obtain Eq. (21).

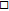
The results in Proposition 3 contain the gauge transformation operators of the CKP and BKP hierarchies:[12–14]

(i) The CKP hierarchy: .

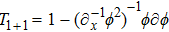(ii) The BKP hierarchy: .

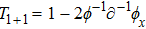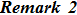In general 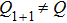, though 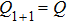, when r = 0 or r = 1.

4. The Gauge Transformation for the Constrained BCr-KP Hierarchy

In this section, we will consider the gauge tranformation of the constrained BC r-KP hierarchy. Before doing this, let us review some results on the gauge transformations of the constrained KP hierarchy first.

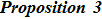[10,13] For the constrained KP hierarchy
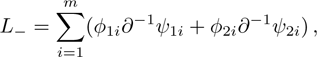
under the gauge transformation 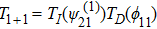, we have
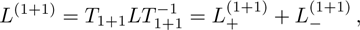
where






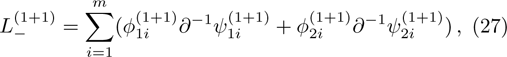
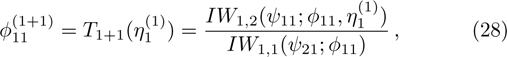
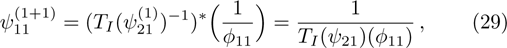
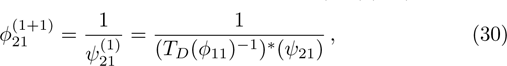
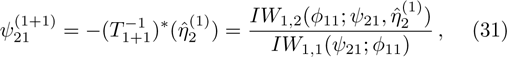
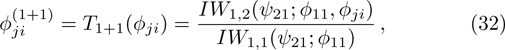
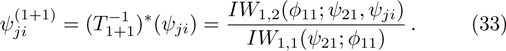
Here , , , .

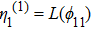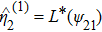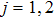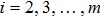As for the case of the BCr-KP hierarchy 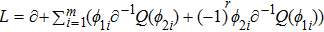, the corresponding gauge transformation operator T has to satisfy the following conditions:

(i) Keeping the Lax equation: 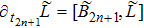, where 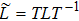and .

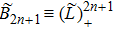(ii) Keeping the BCr-KP constraint: 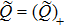, where .

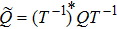(iii) Keeping the form of Lax operator: .

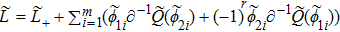The required gauge tranformation operator T is given in the next proposition.

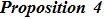For the constrained BCr-KP hierarchy
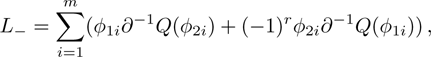
the gauge transformation operator is given by 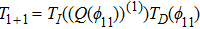. Under the gauge transformation 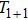, the Lax operator L will become into
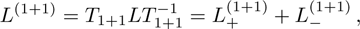
where


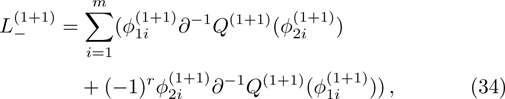
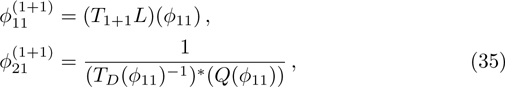
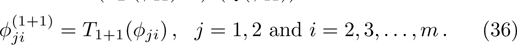
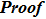In order to prove 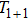is the gauge transformation of the constrained BCr-KP hierarchy, we only need to show

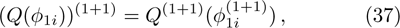
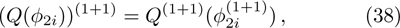
where .

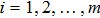When i = 1, according to Proposition 3,

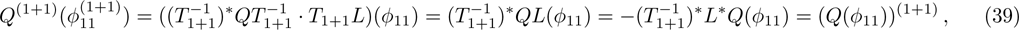
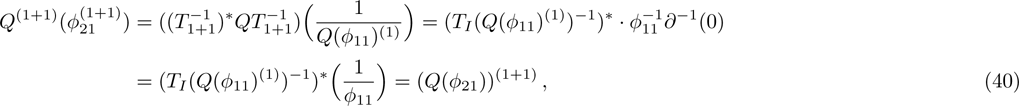
where we have used 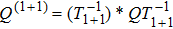, the BCr-KP constraint (8) and .

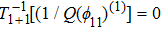For 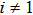and j=1,2,

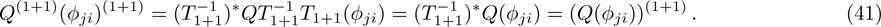
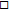
According to Proposition 1 and 4, we can know that

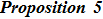For the constrained BCr-KP hierarchy 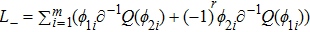, under n-step gauge transformations 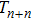, we have
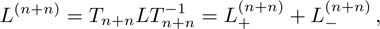
where



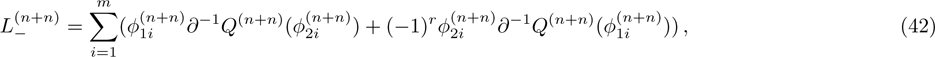
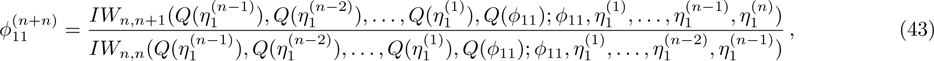
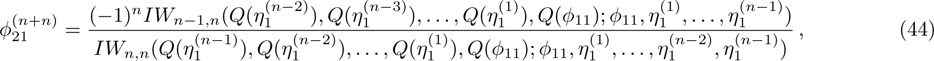
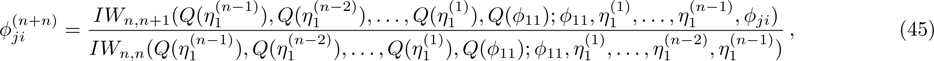
where 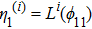, j=1,2, .

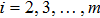When r = 0 and r = 1, the corresponding results in Proposition 5 are consistent with the cases in Ref. [13].

5. The Additional Symmetry and the Gauge Transformation for the BCr-KP Hierarchy

In this section, we will discuss the compatibility of the additional symmetry and the gauge transformation operators for the BCr-KP hierarchy.

At first, additional symmetries for the BCr-KP hierarchy[4] will be introduced. Denote
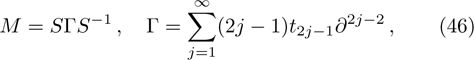
which satisfies 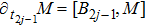and 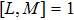. And let
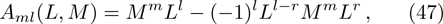
satisfying
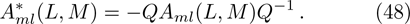
Assume that 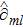are additional independent variable, where 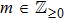and 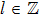. Additional symmetries for the BCr-KP hierarchy are defined by the additional symmetries flows 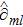, whose actions on the Lax operator and the dressing operator are defined by

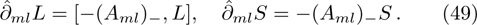
Some lemmas will be needed when we consider the additional symmetries under the gauge transformations for the BCr-KP hierarchy.

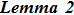For the eigenfunction ϕ of the BCr-KP hierarchy

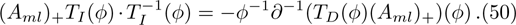
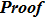By the following direct computations

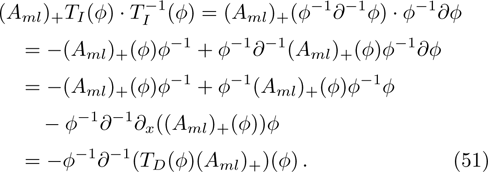
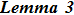For the eigenfunction ϕ of the BCr-KP hierarchy
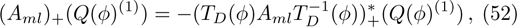
where .

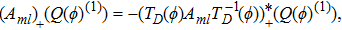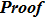According to Eqs. (18), (48), and (50)
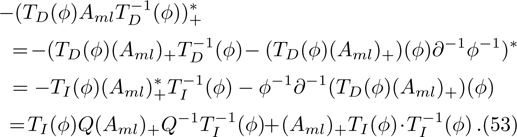
Therefore

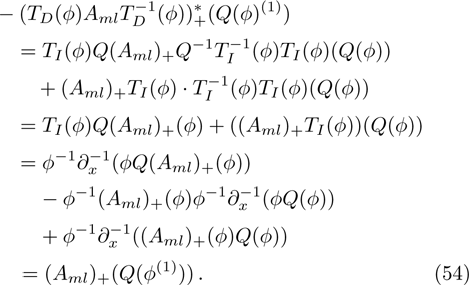
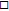
With these preparations, we can get the following results.

For the BCr-KP hierarchy, the additional symmetry flows can commute with the gauge transformations 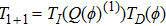, that is

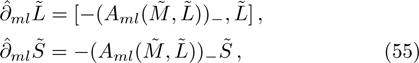
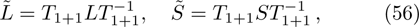
if and only if the eigenfunction ϕ transforms under the additional symmetries in the following way

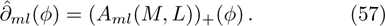
Firstly, according to Eq. (49)
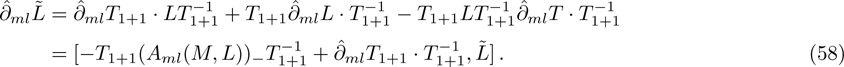
On the other hand
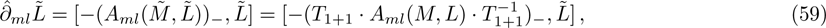
thus Eq. (55) holds, which means
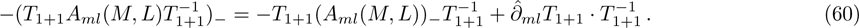
By Eqs. (18), (19), and (52)

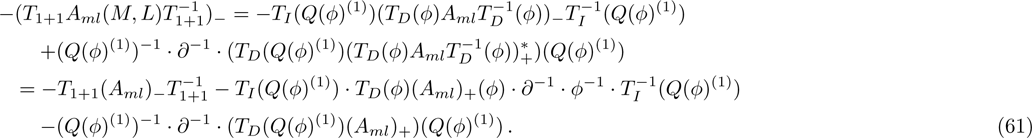
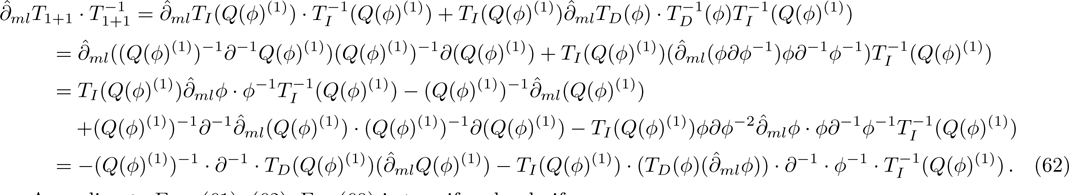
According to Eqs. (61), (62), Eq. (60) is true if and only if

Reference
[1] Date E. Jimbo M. Kashiwara M. Miwa T. Transformation Groups for Solition Equations Nonlinear Inregrable Systems-Classical Theory and Quantum Theory Jimbo M. Miwa T. World Scientific Singapore 1983 39 119 39–119
[2] Dickey L. A. Soliton Equations and Hamiltonian Systems 2 World Scientific Singapore 2003
[3] Date E. Kashiwara M. Jimbo M. Miwa T. J. Phys. Soc. Jpn. 50 1981 3813
[4] Zuo D. F. Zhang L. Chen Q. Rev. Math. Phys. 10 2014 1450019
[5] Loris I. Inverse Problems. 15 1999 1099
[6] Chau L. L. Shaw J. C. Yen H. C. Commum. Math. Phys. 149 1992 263
[7] Oevel W. Phys. A 195 1993 533
[8] Oevel W. Rogers C. Rev. Math. Phys. 5 1993 299
[9] He J. S. Li Y. S. Cheng Y. Chin. Ann. Math. 23B 2002 475
[10] Chau L. L. Shaw J. C. Tu M. H. J. Math. Phys. 38 1997 4128
[11] Cheng J. P. J. Nonlin. Math. Phys. 25 2018 66
[12] Nimmo J. J. C. Darboux Transformations from Reductions of the KP Hierarchy Nonlinear Evolution Equations and Dynamical Systems Makhankov V. G. Bishop A. R. Holm D. D. World Scientific Singapore 168 177 1995 168–77 arXiv:solv-int/9410001
[13] He J. S. Wu Z. W. Cheng Y. J. Math. Phys. 48 2007 113519
[14] Cheng J. P. He J. S. J. Math. Anal. Appl. 410 2014 989
[15] He J. S. Li Y. H. Cheng Y. SIGMA 2 2006 060
[16] Cheng J. P. Wang J. Z. Zhang X. Y. J. Nonlin. Math. Phys. 21 2014 533
[17] Geng L. M. Chen H. Z. Li N. Cheng J. P. Mod. Phys. Lett. B 32 2018 1850176
[18] Li N. Cheng J. P. Z. Naturforsch. A 73 2018 345
[19] Oevel W. Darboux Transformations for Integeable Lattice Systems Nonlinear physics Alfinito E. Martina L. Pempinelli F. World Scientific Singapore 233 240 1996 233–40
[20] Liu S. W. Cheng Y. He J. S. Sci. Chin. Math. 53 2010 1195
[21] Li M. H. Cheng J. P. He J. S. Z. Naturforsch. A 71 2016 1093
[22] Dickey L. A. Commun. Math. Phys. 167 1995 227
[23] Orlov A. Y. Schulman E. I. Lett. Math. Phys. 12 1993 171
[24] Adler M. Shiota T. van Moerbeke P. Phys. Lett. A. 194 1994 33
[25] Fokas A. S. Fuchsstiner B. Phys. Lett. A 86 1891 341
[26] Oevel W. Fuchssteiner B. Phys. Lett. A 88 1982 322
[27] Chen H. H. Lee Y. C. Lin J. E. Phys. D 9 1983 439
[28] Fuchssteiner B. Prog. Theor. Phys. 70 1983 1508
[29] Tu M. H. Lett. Math. Phys. 81 2007 91
[30] Cheng J. P. Tian K. L. He J. S. J. Math. Phys. 52 2011 053515
[31] Li C. Z. He J. S. Rev. Math. Phys. 24 2012 1230003
[32] Cheng J. P. Acta Math. Sic. 35B 2015 1111
[33] Wu C. Z. Phys. D 249 2013 25
[34] Wu C. Z. Adv. Math. 36 2017 603
[35] Liu S. W. J. Math. Phys. 56 2015 113505