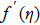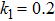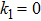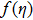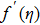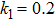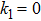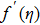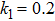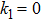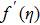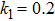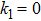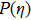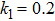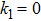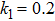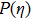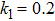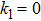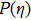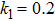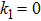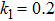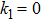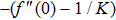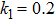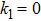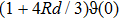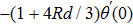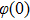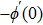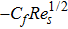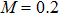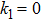† Corresponding author. E-mail:
A numerical analysis is developed for incompressible hydromagnetic viscous fluid passed through a curved stretching surface. Fluid saturated by porous space is bounded by curved surface. Term of porous medium is characterized by implementation of Darcy-Forchheimer theory. Adequate similarity variables are implemented to develop a system of non-linear ordinary differential system of equations, which govern the flow behavior. The impact of radiation constraint and Eckert number is incorporated in the energy equation. Numerical scheme based on RKF45 technique is implemented to solve the derived flow model. Prescribed heat flux (PHF) and prescribed surface temperature (PST) boundary conditions are utilized on temperature with Prescribed Surface Concentration (PSC) and Prescribed Mass Flux (PMF) on concentration. Flow behavior is discussed for both the slip and no-slip conditions. Dimensionless physical quantities are presented through graphs and tables.
μ
dynamic viscosity
ρ
fluid density
(u,v)
components of velocity
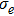
electric conductivity
p
pressure
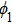
porosity of porous medium
cb
form of drag
DB
diffusion coefficient
k1
permeability of porous medium
C
concentration
T
temperature
qr
radiative heat flux
Re
magnetic Reynolds number
B
0
magnitude of magnetic field
a
stretching constant
L
slip parameter
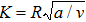
dimesnionless radius of curvature
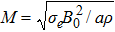
magnetic parameter
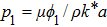
porosity parameter
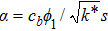
local inertia parameter
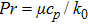
Prandtl number
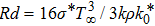
radiation parameter
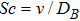
Schmidt number
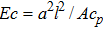
Eckert number
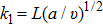
slip length
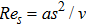
local Reynolds number
Cooling of filaments or continuous strips, paper production, metallic plate cooling placed in cooling bath, glass blowing, artificial fibers, wire drawing and extrusion of rubber sheets are some practical applications of fluid flow passing through stretching surfaces. Polymer industry plays a major role in the process of molten polymers manufacturing with the help of slit die for the production of plastic or fiber sheet. Such materials travelled between wind-up and feed roll or through conveyor-belts describing the behavior of stretched surfaces.[1] The mechanical characteristics of the product strictly depend on the heat transfer rate through stretching surfaces. Boundary layer approximation is used for the solutions and hence not comprises the exact solution of Navier-Stokes equation.[2–3] However Crane[4] presented a similarity solution in closed and exact form for viscous fluid owing to a linear stretching surface. Many researchers extended the Craneʼs idea by including different physical features like injection/suction, magnetic field, analysis of heat transfer etc. The combined influence of mass and heat transport analysis was presented by Gupta and Gupta[5] over porous stretched surface considering the injection/suction cases. Wang[6] investigated viscous flow through a stretched surface in view of suction and surface slip. The flow analysis of micropolar fluid past through stretching/shrinking surface was analyzed by Zheng et al.[7] Unsteady boundary layer viscous fluid problem corresponding to a stretching sheet was discussed by Rashidi and Pour.[8] Sheikholeslami et al.[9] reported the flow problem of nanofluid past stretched wall. Many researchers investigated different flow models along flat surfaces.[10–14]
The flows embedded in porous medium generated a remarkable interest between the scientists owing to their wide practical applications in industry such as geothermal systems, porous insulation, packed beds, fossil fuels, extraction of crude oils, food storage, petroleum technology and disposal of waste materials etc.[15–17] Different models like Darcy and Brinkman, and Darcy-Forchheimer-extended was presented in literature to explain physical and mathematical features in the porous medium. Researchers are curious to study the models related to porous media. Such models are developed in view of Darcyʼs law in which pressure gradient is in direct relationship with volume average velocity. Darcyʼs formula is capable for slower velocity and lesser porosity while excluding the influence of thermal dispersion, inertia forces, variable porosity and solid boundary. The addition of non-Darcian impacts is very essential in the analysis of porous medium in order to achieve the desired accurate results. Such impacts are introduced by Forchheimer[18] with the addition of the term named square velocity in the term of Darcian-velocity. After that Muskat[19] named such term as “Forchheimer term” which is applicable for high Reynolds number. Seddek[20] reported the analysis of thermophoretic velocity effect in Darcy-Forchheimer porous space by considering the convective flow of viscous liquid. Pal and Mandal[21] considered the convective diffusion in hydromagnetic viscous fluid flow in a non-Darcy porous space under the aspects of heat sink/source. Gireesha et al.[22] addressed the numerical modeling of boundary layer liquid through non-Darcian effects.
In all the work cited above authors considered flow models over flat surfaces. Cartesian co-ordinates are implemented for the modeling of the problem. Fluid passed through curved moving surfaces has practical implications in stretch-forming machines owing to curve jaws. A numerical problem of viscous fluid by curved stretched surface was first discussed by Sajid et al.[23] Curvilinear co-ordinates were utilized for the governing equations. Later Sajid et al.[24] extended his work to the flow of micropolar fluid through curved sheet. The results show that pressure can not be neglected within the boundary layer in contrast with the flat stretching surface. The same problem was modified by Naveed et al.[25] by considering the phenomenon of heat transportation. Naveed et al.[26] reported the unsteady hydromagnetic flow of viscous fluid through a curved surface. Buongiorno model was implemented to find the numerical solution of curved sheet problem by Naveed et al.[27] Rosca and Pop[28] studied flow of unsteady viscous fluid by curved stretching/shrinking sheet. Imtiaz et al.[29] analyzed analytically unsteady hydromagnetic viscous fluid through curved sheet. A numerical problem of viscous fluid owing to non-linear stretched curved sheet was constructed by Sanni et al.[30] Abbas et al.[31] reported the flow model of viscous liquid.
The combined influence of heat with mass transfer over flat surfaces has gained considerable interest among the researches due to its significance importance in chemical industries and metallurgy like polymer extrusion, continuous casing, metal spinning, food processing, temperature distribution to agriculture fields and flow in desert cooler. More importantly polymer industry has main operation of extrusion of plastic sheets. The process involves the transfer of heat between surrounding fluid and the surface. Melt issue from slit is expanded in order to acquire the required quality in manufacturing process of sheet. Thermal radiative flow is important for industrial purposes such as nuclear plant, air craft, design of equipments, gas turbines, space vehicles, satellite etc. In the perspective of space machinery, few devices are produced to function at large temperature for the achievement of higher thermal efficiency. Hence radiation impact is very important in the process of high temperature while studding the thermal effects. Rashidi et al.[32] investigated hydromagnetic viscous fluid flow problem due to a vertical sheet incorporating the influence of radiative heat with mass transfer. Rashidi et al.[33] reported the problem of thermally radiative nanofluid due to stretched surface. Pal et al.[34] discussed the influence of thermal radiation in nanofluids through stretching/shrinking surface. A numerical study on three dimensional nanofluid flow through stretching sheet under solar radiation was examined by Rauf et al.[35] Hayat et al.[36] reported the thermal radiation effect on Maxwell nanofluid flow passed through a stretching surface.
The intention of the current study is to elaborate the numerical outcomes of thermally radiative flow of hydromagnetic viscous fluid subject to the stretching surface with mass transfer. The stretching surface is drenched into non-Darcy permeable medium. Prescribed heat and mass flux conditions on temperature and concentration with slip and no-slip conditions on velocity are utilized. The results are also discussed for prescribed surface temperature and concentration cases. According to the authors’ knowledge, till now no such study is reported in the literature. Problem formulation is illustrated in Sec.
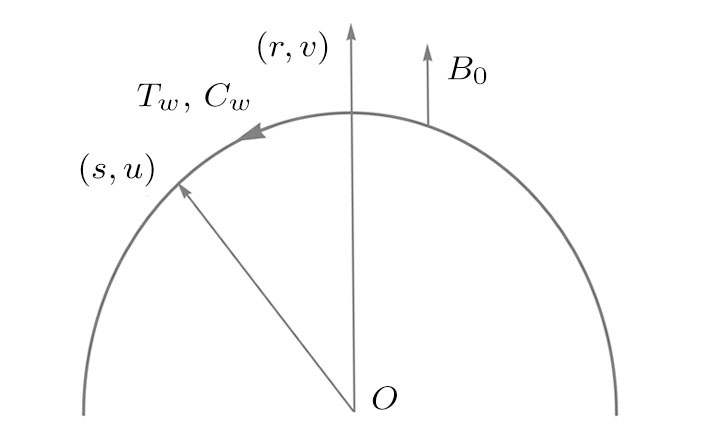
We consider incompressible radiative two dimensional MHD flow of viscous fluid over a stretched curved surface with radius R. The surface is submerged in the non-Darcy porous medium. The r-axis is taken normal to the direction of flow. To make the sheet stretched, we apply opposite forces of same magnitude at the ends of curved surface along s-direction by fixing the origin. A magnetic field with magnitude B
0 is functional along transverse direction as mentioned in Fig. 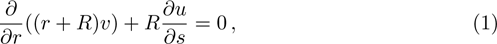

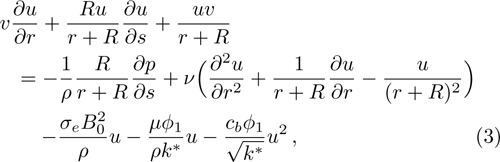
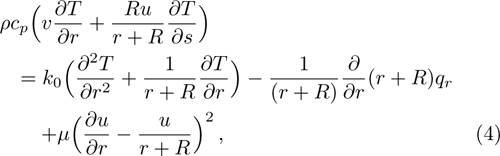
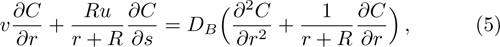
The suitable conditions suggested for the flow problem are:[37]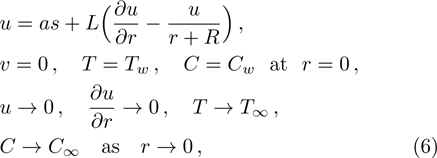
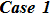
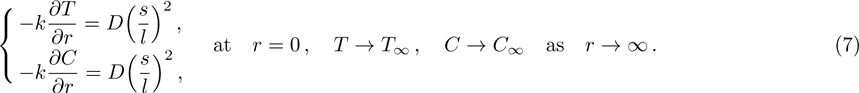
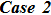
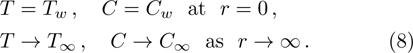
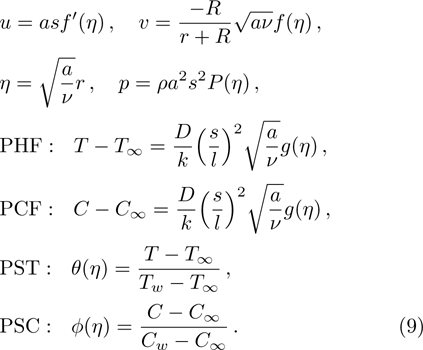
The continuity equation (
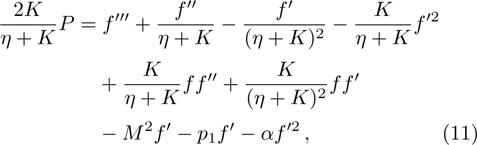
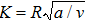
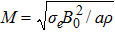
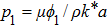
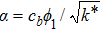
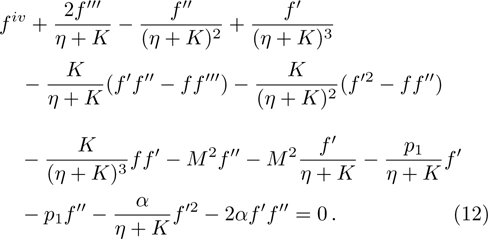
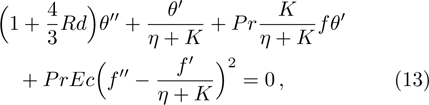
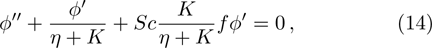
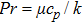
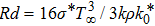
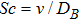
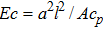
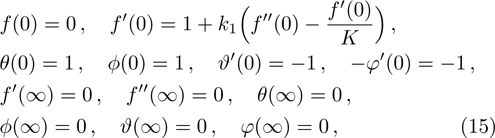
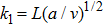
The physical quantities of our interest are the skin friction co-efficient, local Nusselt number and Sherwood number along s-directions, which take the following form: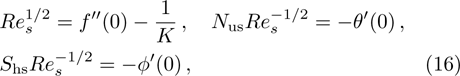
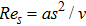
Runge-Kutta-Fehlberg fourth fifth order (RKF45) technique, mainly based on the numerical method that is helpful for the solution of the equation 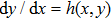
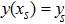
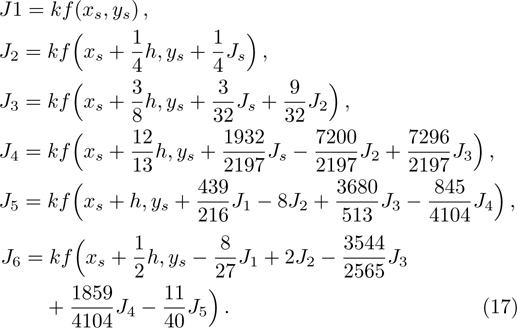
Order 4 approximation to the solution is: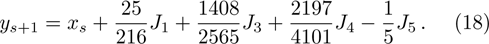
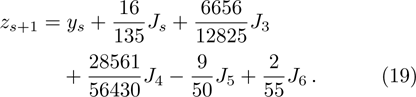
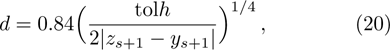
Our key objective is to transform first the system (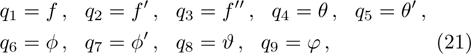
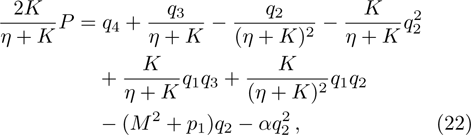
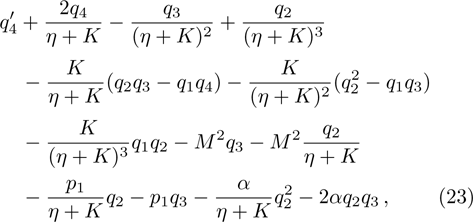
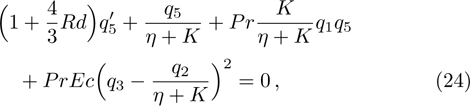
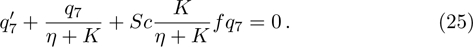
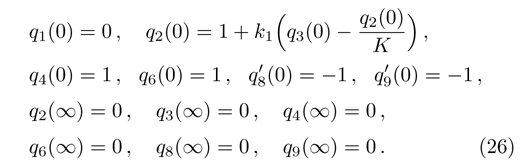
We studied the two-dimensional viscous fluid flow over a curved sheet. We implement Runge-Kutta-Fehlberg forth-fifth (RKF45) order technique[34] to obtain a numerical solution of Eqs. (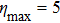
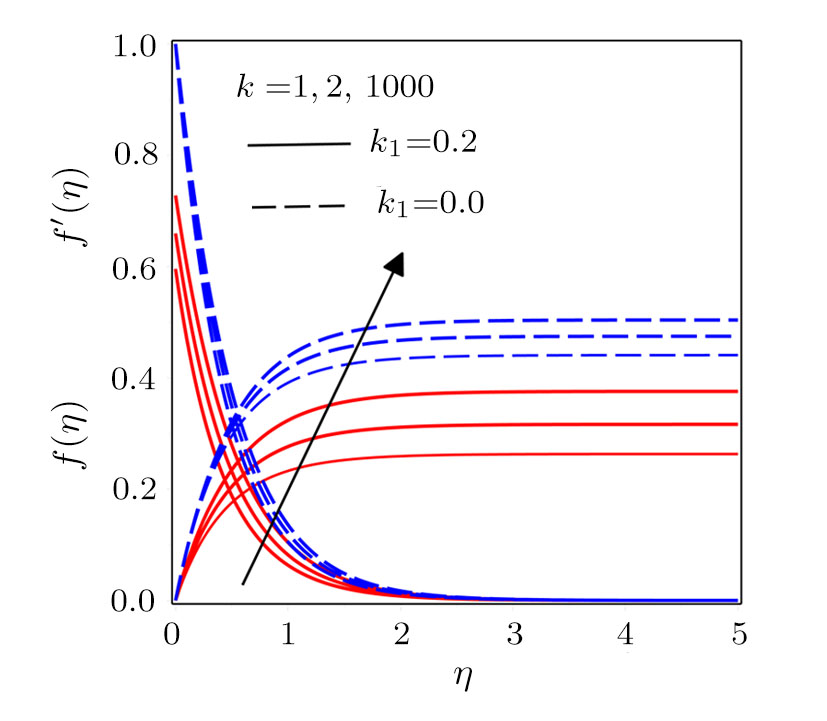
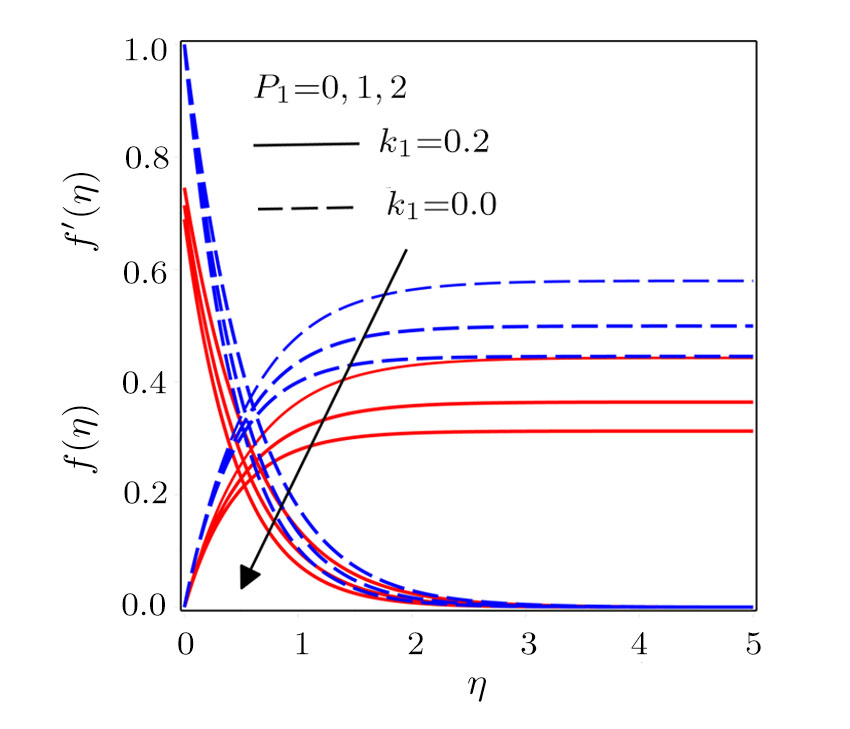
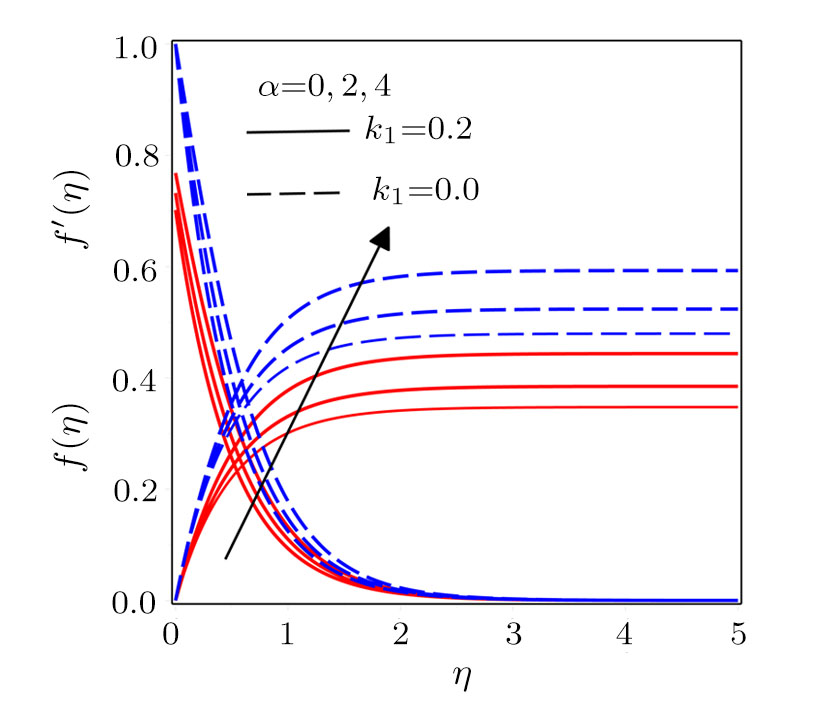
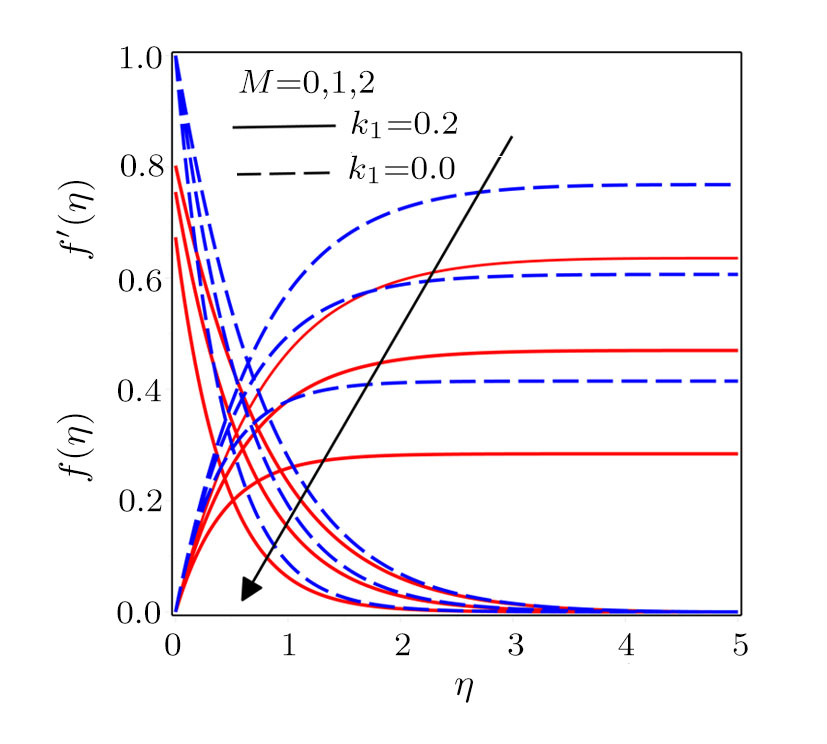
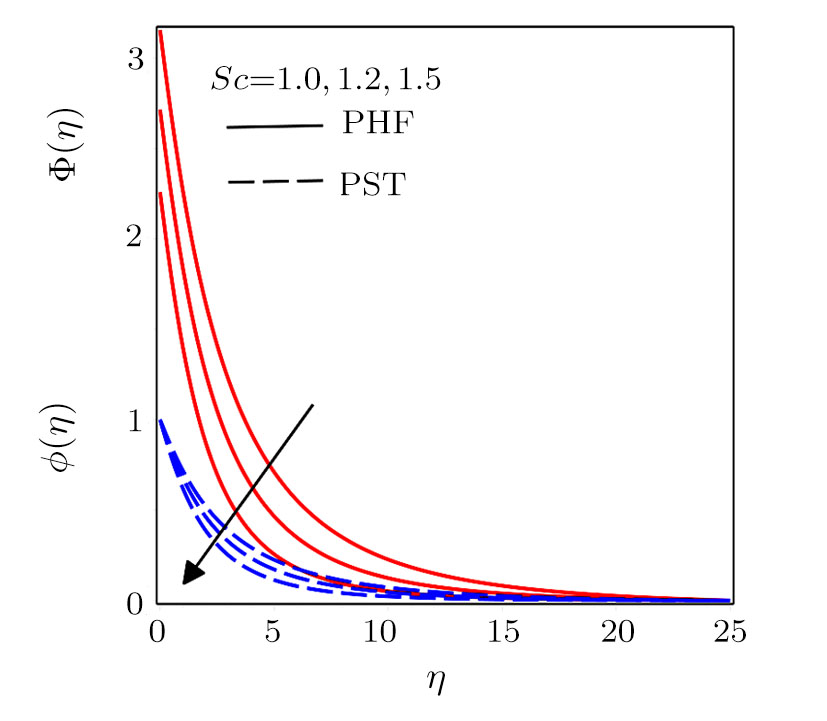
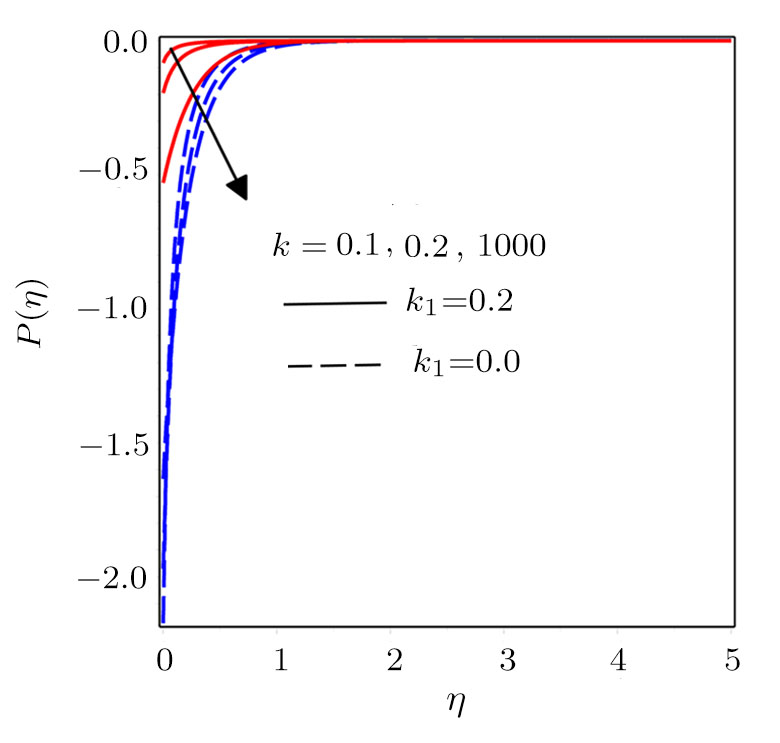
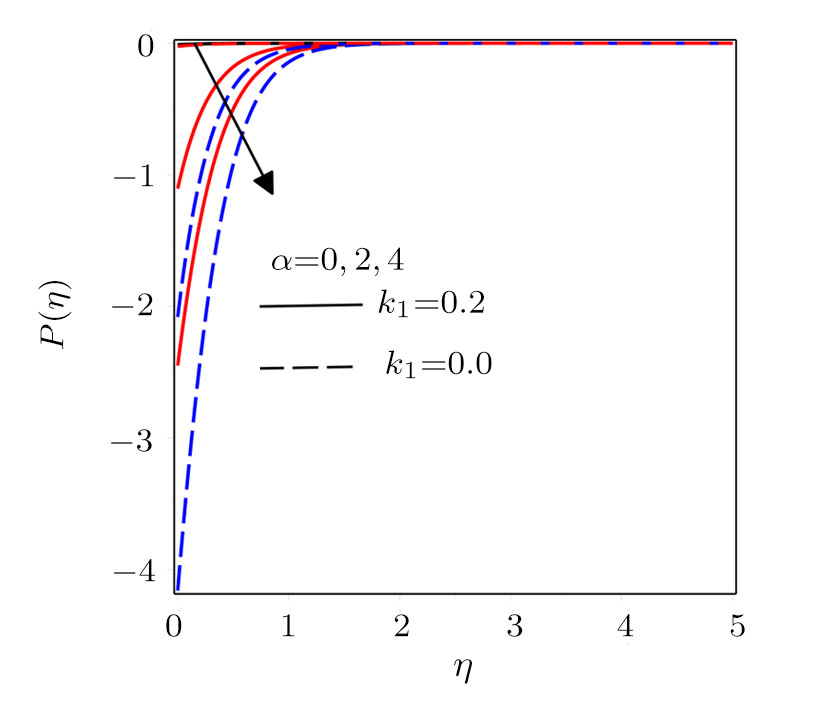
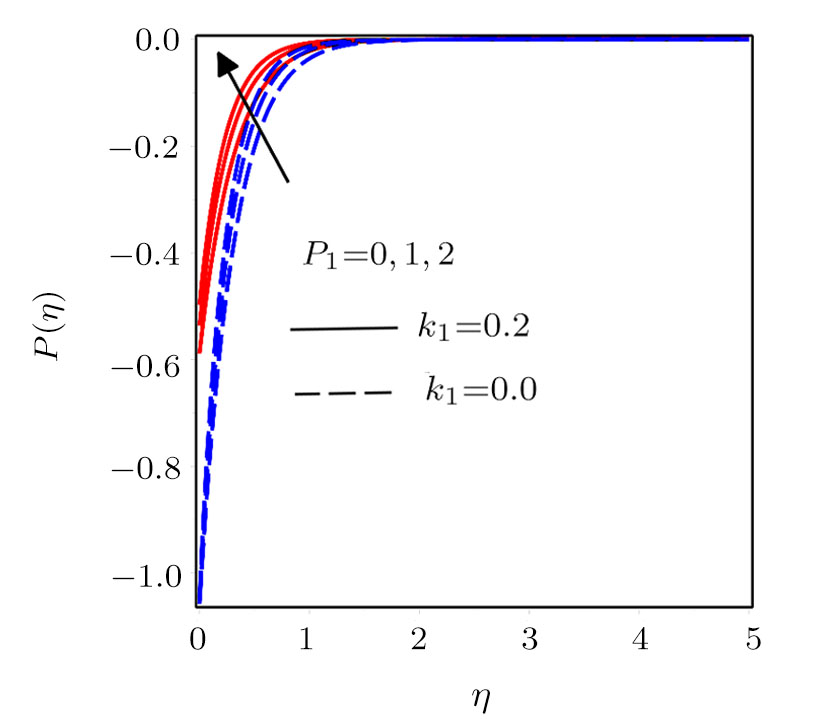
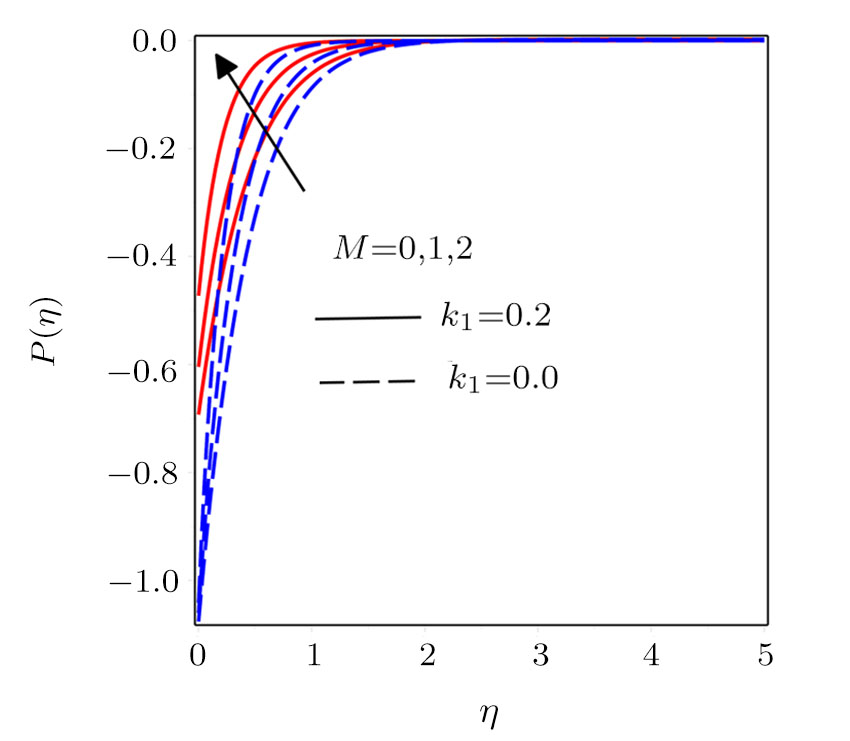
Figure 
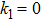
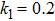
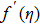
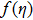
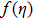
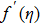
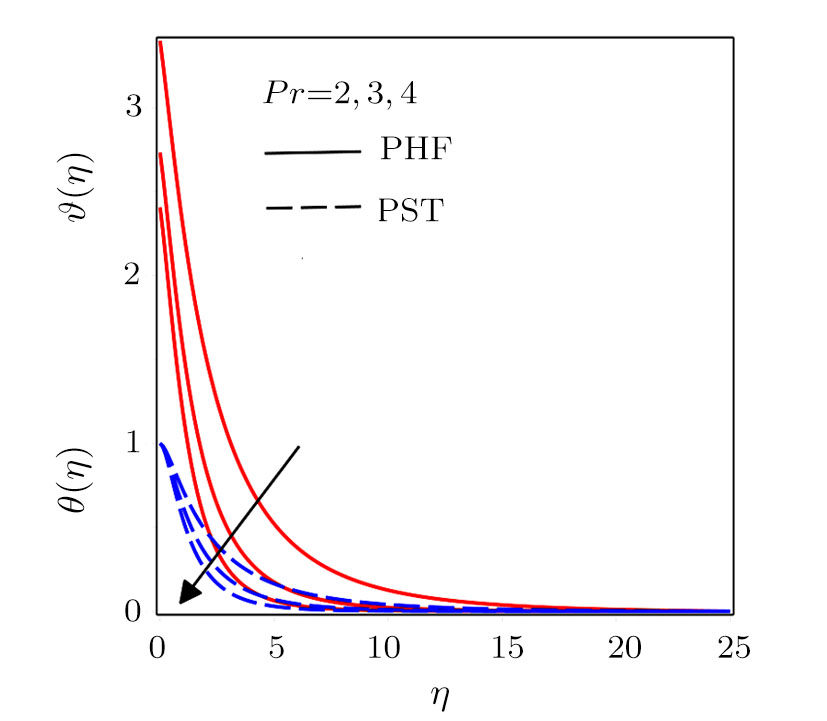
Figure 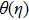
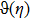
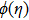
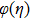
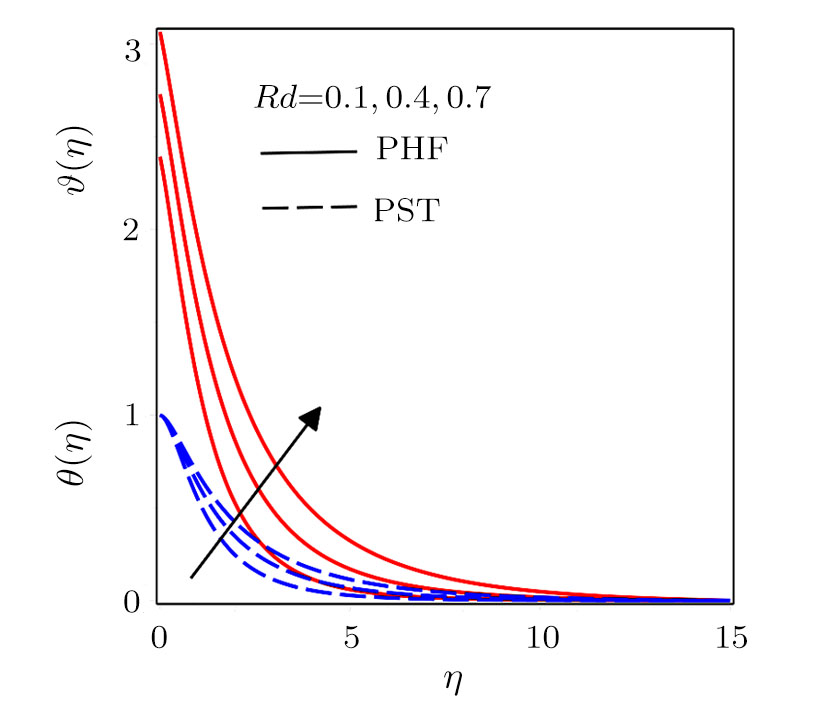
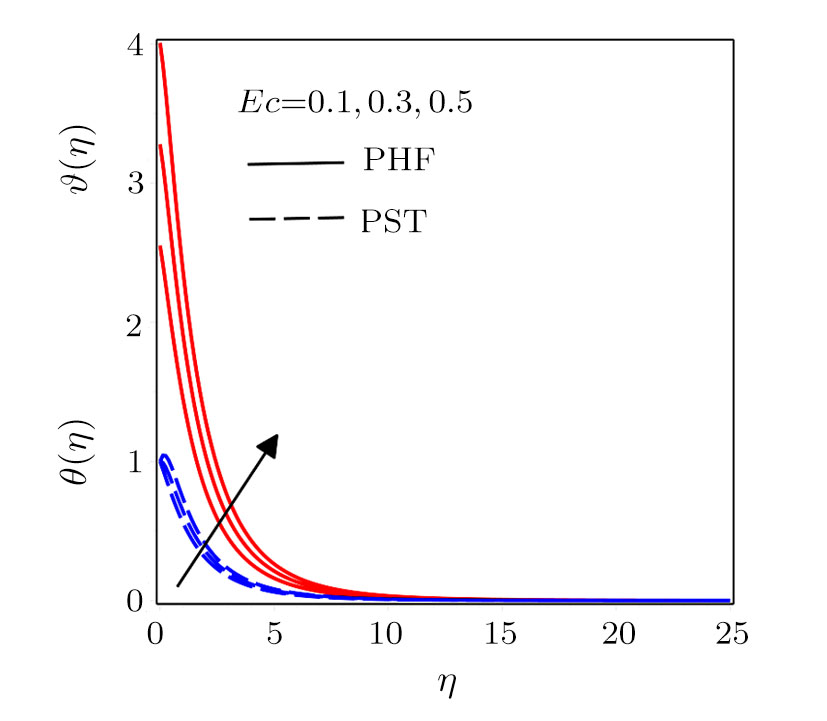
Figure 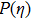
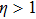
Table 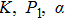
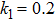
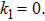
| Table 1.
Shear stress at sheet for various values of K, p
1, α, and M at different conditions |
| Table 2.
Heat transfer rate at sheet for various values of Pr, Rd, and Ec at different conditions PHF and PST. . |
| Table 3.
Mass transfer rate at sheet for various values of Sc at different conditions PMF and PSC. . |
| Table 4.
Relative values of |
Darcy-Forchheimer flow of hydromagnetic viscous fluid passed through a curved stretching is analyzed in the presence of heat and mass transfer. Radiation and viscous dissipation terms are incorporated in the energy equation. RKF45 method is implemented to obtain the solution of the resultant system of non-linear equations. The results are discussed through graphs and tables of the emerging dimensionless parameters. Subsequent conclusions can be made for the present numerical analysis: (i) Velocity profiles rise due to the variations in radius of curvature and local inertia co-efficient parameter while a fall in such profiles is seen for different values of porosity and magnetic parameters. (ii) Variations in Prandtl number and radiation parameter have opposite influence on temperature profiles. (iii) Enhanced values of Schmidt number declined the concentration profiles. (iv) Pressure profiles decay for larger values of inertia co-efficient parameter and radius of curvature while the profiles climb for rising values of porosity and magnetic parameters. (v) Increased values of radiation parameter amplify heat transfer rate. (vi) Heat transfer rate reduce in case of PST and enlarge for PHT by varying Eckert number.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] |