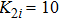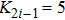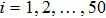† Corresponding author. E-mail:
Migration is ubiquitous in ecosystem and often plays an important role in biological diversity. In this work, by introducing a time-varying migration rate associated with the difference of subpopulation density into a prey, we study the Hopf bifurcation and the critical phenomenon of predator extinction of the three species prey-predator system, which consists of a predator, a prey and a mobile prey. It is found that the system with migration exhibits richer dynamic behaviors than that without migration, including two Hopf bifurcations and two limit cycles. Interestingly, the parameters of migration have a drastically influence on the critical point of predator extinction, determining the coexistence of species. Moreover, the population evolution dynamics of one-dimensional multiple prey-predator system are also discussed.
The prey-predator (PP) model has been one of the research hotspots in the interdisciplinary fields of bio-mathematics and biophysics since it was put forward in 1932.[1] The classical PP model assumes that the prey is in ideal natural environment, and the predator can only rely on the prey to survive. To incorporate the actual ecological environment more effectively, a lot of improvements were made in the classical model, such as functional response,[2] noise,[3] diseases,[4] refuge,[5] Allee effects,[6] and so on.[7–12] To reflect the intake rate of a predator as a function of prey density, several types of functional reactions on the basis of experiments were proposed,[13] including the prey-dependent and the predator-dependent. Of which the most popular functional response model today is Hollingʼs type 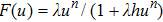
In fact, migration behavior is a ubiquitous physical phenomenon in natural ecosystems.[17] Some literatures have theoretically analyzed and numerically simulated PP systems with diffusion and migration,[18–21] for example, Liu found that the PP system with migration could emerge travelling pattern.[21] Sun et al. studied the conditions of Hopf and Turing bifurcation critical line in the spatial domain of prey-predator model with cross diffusion, and proved that cross diffusion could create stationary patterns.[22] It is valuable to develop a PP model with migration effect related to multiple system dynamics. Nishimura et al. investigated the coupled double systems with density-dependent migration, and found the migration mechanism with intra-system and inter-system population competition could solve the spatial isolation of ecosystem.[23] Nevertheless, all the studies so far have either considered migration and diffusion in the case of a single system, that is, migration and diffusion happens in the intra-system, or assumed each species employing identical migration mechanisms. Note that, in reality a large ecosystem usually consists of multiple subsystems, and individuals migrate between interconnected subpopulation through channels with time-varying rate. It is therefore interesting to ask how the migration rate would influence the system dynamics of PP model, for instance, how the critical point of predator extinction would depend on such a time-varying migration rate? The answer to this question may provide useful instructions regarding the species diversity in ecosystem.
In the present work, we construct a time-varying migration function related to subpopulation density by using cubic flux-controlled memristor model. We find that the different bifurcation behavior of the subsystem and the critical point of predator extinction is changed by controlling the parameters of the time-varying migration of a prey, which leads to two Hopf bifurcations, two limit cycles. Moreover, it would form a spatiotemporal pattern of the predator in one-dimension space for multiple PP model with time-varying migration. The paper is organized as follows: in Sec.
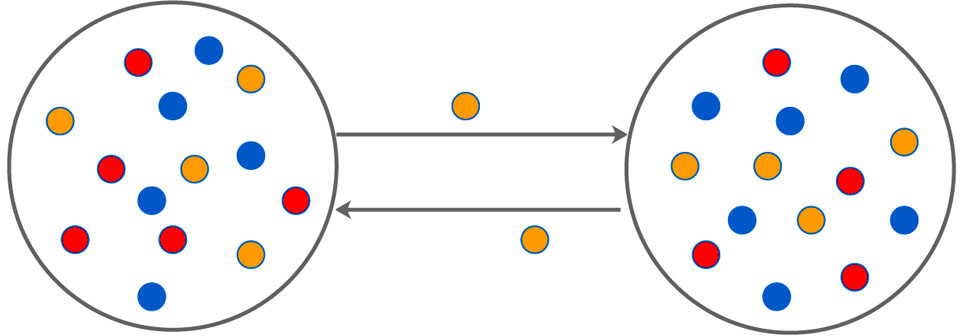
We extend the classical two species PP model to a three species one, one kind of predator and two kinds of prey, where the prey includes a less adept one that was more likely to be captured, and a smarter one that was easy to escape through narrow channels between spatially separated parts of the system with a time-varying rate. Note that if the other prey or predator migrate too, the simulation results are similar to that of the present work (not shown here). The schematic illustration of the model is shown in Fig.
According to the stochastic simulation schemes, one may write down the following set of dynamic equations at a mean-field level: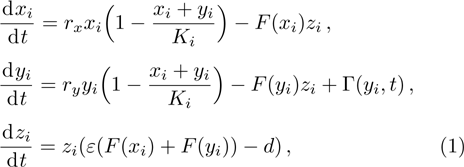
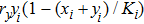
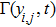
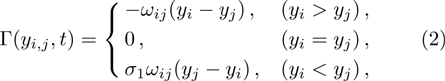
As we all know, the reasons of species migration in ecosystems are complex and there are many influencing factors,[24] such as intra-population competition, reproductive migration, weather and environmental change, and even human influence, etc. Here, we assume that the prey migration is a time-dependent function related to the population density under the following consider.[25] The increasement of the predator results in the prey decrease, which causes the predator decrease in turn; while the decreasement of the predator leads to the prey increase, and then render the predator increase. This phenomenon is similar to the memristor effect. Inspired by this, we build a time-varying migration function associated with population density by using the cubic flux-controlled memristor model as follows,[26–27] which has been successfully applied to the biological neural networks:[28–29]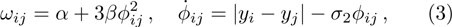
In what follows, a fixed time step is set as 0.001. Other parameters rx = 0.55, ry = 0.71, h = 1.48, λ = 0.68, d = 0.485, α = β = 0.02, and the fourth-order Runge-Kutta method is employed to solve Eqs. (
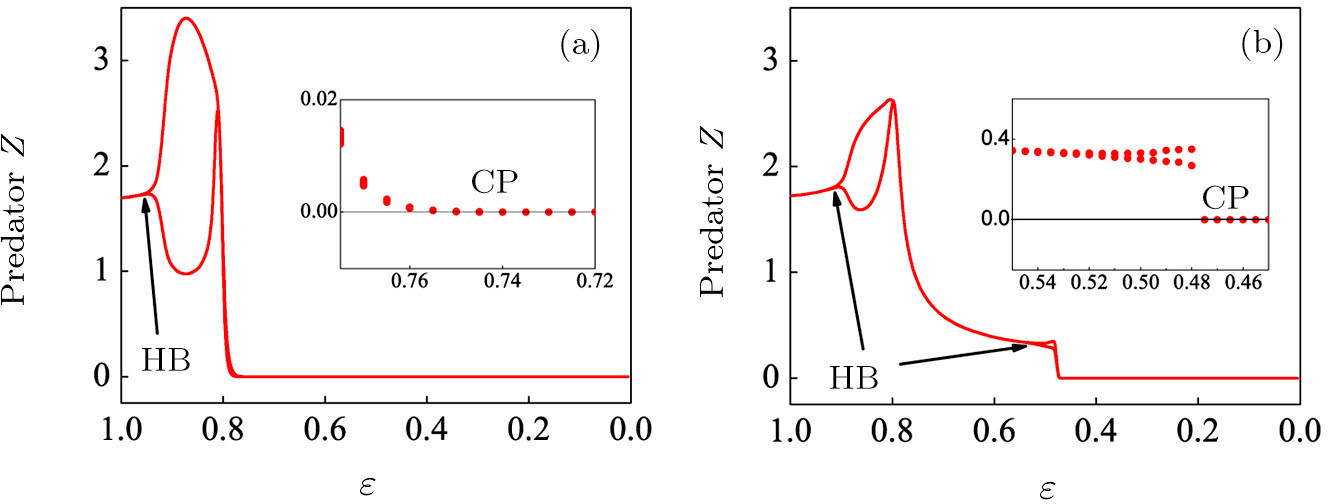
To begin, we select the conversion rate ε of digested prey per unit time by predator as the controll parameter to investigate the bifurcation behavior of the predator, and the range of ε belongs to (0, 1.0). The initial state of the system is randomly set to (xi, yi, 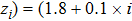
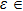
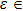
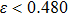
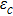
Figure
 | Fig. 3. Four typical phase portraits of the double-system for ε = 0.38 (a), ε = 0.49 (b), ε = 0.84 (c), and ε = 0.94 (d). |
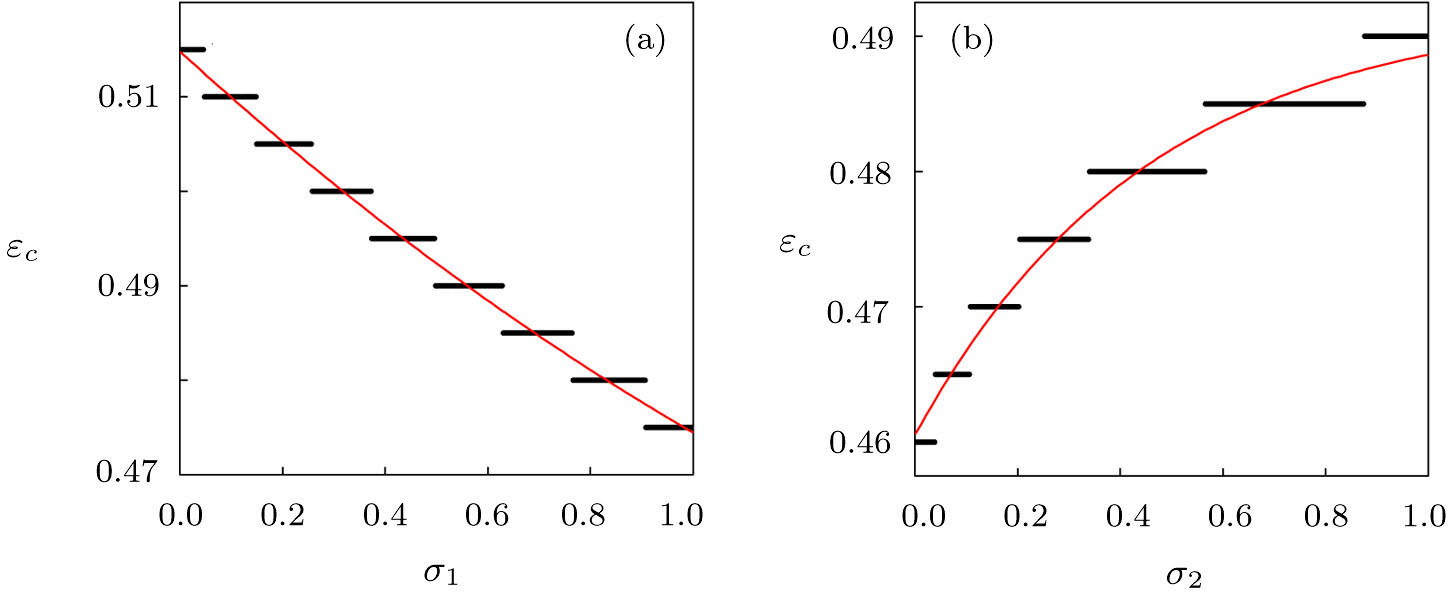
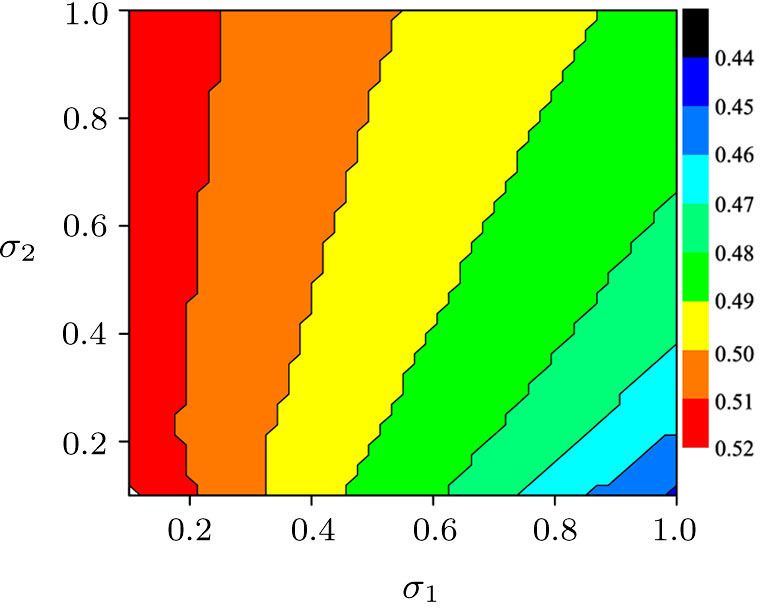
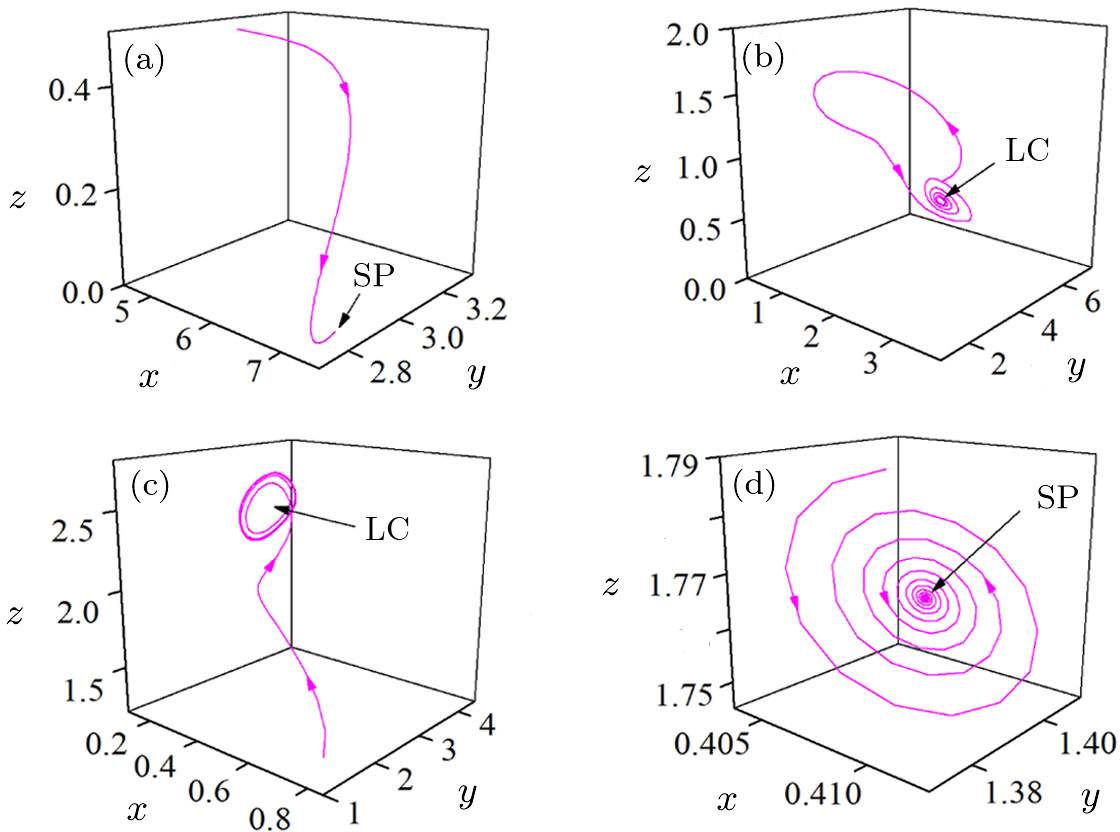
To further investigate the influence of the migration parameters σ1 and σ2 on the critical point of predator extinction, we fix the step size of the migration parameters to be 0.001 to change between (0, 1) and stipulate that extinction occurs when the population density is less than 10−5. Firstly, we fix σ2 = 0.5, and plot the εc as a function of σ1, as shown in Fig.
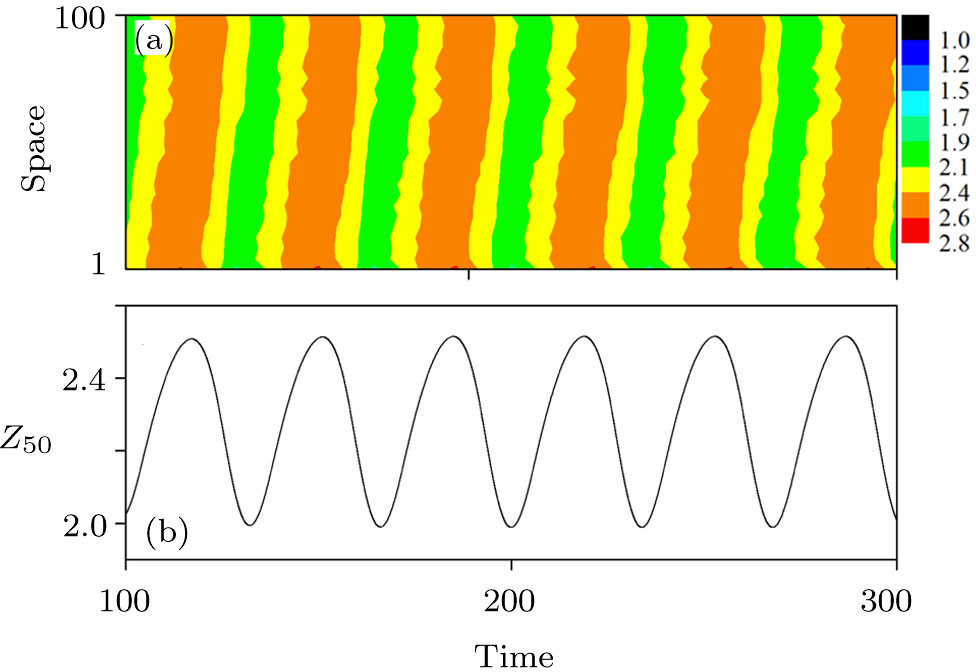
In addition, to check whether the population density evolves into a periodic solution when the pattern is formed, and also to further confirm that our proposed PP model with time-varying migration has the reliability of simulating real ecosystems, we allocate an array of subsystems with different maximum environmental carrying capacity 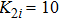
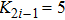
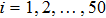
In summary, we have studied the effects of migration on the dynamics of three species PP system, which consists of one predator and two prey live in more than one subsystems. For simplicity, however, only one prey is considered to migrate among subsystems. To better characterize the feature of migration, we employ a cubic flux-controlled memristor model to construct a time-varying migration rate associated with the densities of subpopulation. By comparing the dynamic behaviors of PP system with and without migration, it is found that the three species PP system with migration exhibits rich dynamics, such as two Hopf bifurcations, two limit cycles, and a critical extinction point of the predator. Particularly, the migration of prey leads to the significant decrease of the critical value for the predator extinction, suggesting that the migration of prey is in favor of the survival of predator. In other words, if we intend to enhance the species diversity of an ecosystem, the prey should be driven to migrate between subsystems. Furthermore, we investigate the spatiotemporal dynamics of one-dimensional multiple PP system, and find that the system evolves into a stable evolution pattern after a period of time. Our results may provide valuable ideas for further study and preserving biological diversity in ecosystems.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] |