Cite this Article
Hu Qiang-Lin, Luo Xiao-Bin, Xiao Gui-Lan, Hu Wen, Peng Ji-Chang, Zhou Shen-Lin. Linear Analyses of Langmuir and EM Waves in Relativistic Hot Plasmas. Communications in Theoretical Physics, 2018, 70(5): 609  
Permissions
Linear Analyses of Langmuir and EM Waves in Relativistic Hot Plasmas
Hu Qiang-Lin1, †, Luo Xiao-Bin1, Xiao Gui-Lan2, Hu Wen1, Peng Ji-Chang1, Zhou Shen-Lin1
Department of Physics, Jinggangshan University, Ji’an 343009, China
Library, Jinggangshan University, Ji’an 343009, China

 

† Corresponding author. E-mail: qlhu@jgsu.edu.cn

Supported by the National Natural Science Foundation of China under Grant Nos. 11064005 and 51460020, and the financial support provided by the Key Subject of Atomic and Molecular Physics in Jiangxi Province (2011-1015).

Abstract
Abstract

The linear Langmuir and electromagnetic (EM) waves in relativistic hot plasmas are discussed, and the dispersion relations are obtained based on the covariant Maxwell’s and fluid equations. When kBT/mc2 ˃ 1, the effective mass of electrons will be increased obviously. As the results, many other influences are induced, such as the decrease of the plasmas frequency and the critical frequency, the reduction of the electron sound velocity and the electrons’ oscillation velocity, and so on. Numerical results show that these influences can affect the dispersion relations of Langmuir and EM waves seriously even in linear regime.

Keyword:relativistic hot plasmas;Langmuir wave;electromagnetic wave;dispersion relation
1 Introduction

Previous studies in laser-plasmas interactions discovered many interesting phenomena, such as filamentation,[1–2] modulation instability,[3–4] stimulated Raman scattering,[5] and so on. Most of the analyses of these phenomena assumed electrons’ thermal energy much small compared to their rest energy, i.e., kBT ≪ mc2, where kB is the Boltzmann constant, T is the plasmas temperature, m is the rest mass of electron, and c is the light speed in vacuum. These kinds of plasmas are the so-called cold or warm plasmas. However, in some particle-in-cell (PIC) simulations of kJ class laser channeling in mm scale underdense plasmas for fast ignition, the residual electron temperature T in the channel was found to be multi-MeV, i.e., kBT ˃ mc2.[6–7] Relativistic T was also observed in PIC simulations with sub-ps intense pulses of energy as low as 10 J.[8] Recently, a plasma as hot as a few tens of MeV has been numerically demonstrated by using the state of the art high-power laser facilities.[9] Furthermore, it is also believed that the relativistic hot plasma existed widely in the early period of evolution of the Universe.[10]

The relativistic effect of the random motion can increase the effective mass of the charged particles. It will trigger a series of changes in the laser-plasmas interaction, such as decrease the plasmas frequency, reduce the electron oscillation velocity, decouple the laser from the plasmas, and so on.[6–8] Finally, these variations will affect a wide range of plasma optical phenomena in intense laser-plasma interaction.[10–14] In present, how relativistic T affects the plasma optical process still remains largely unexplored.[12]

The theoretical approach to analyse the relativistic hot plasmas need a fully and coherent relativistic plasma equations, and which has been established.[10,13] Most of the earlier studies ignore completely relativity in the continuity equation or work only in the weak relativity approximation in which the relativistic effects are taken into account making use of a motion equation obtained by simply substituting the velocity of species u by γu in the nonrelativistic Euler’s equation.[15] In contrast, the fully and coherent relativistic plasma equations are derived from the covariant formulation of energy-momentum tensor, and can be regarded as fully relativistic in terms of the magnitudes of the speed and temperature of the fluid element.[10,13]

In this letter, we analyse the Langmuir and EM waves in relativistic hot plasmas linearly based on the fully and coherent relativistic plasma equations and Maxwell’s equations. The dispersion relations are obtained. We will show that in the relativistic hot plasmas, the increase of the electron effective mass reduce the electron sound velocity and critical frequency as well as the electron oscillation velocity and the plasmas frequency. Numerical results show that these variations can affect the dispersion relations seriously.

2 Basic Equations

The fluid equations used to describe the dynamics of fully relativistic plasmas and the EM field equations for the scalar and the vector potentials can be obtained from the conservation of the particle number and the energy-momentum tensor for each species of plasmas, and can be written as,[10,13,16]

where ϕ and A are the scalar and the vector potentials of EM field, qa is the particle charge, the subscript a represents a-species of particles in plasma, na represents the particle density in the rest frame of plasma, ua is the fluid velocity normalized by the speed of light c, is the relativistic Lorentz factor induced by oscillation motion of a-species charged particles in the laser field,

is the enthalpy per fluid particle, ma, Ta, na0, and α represent the rest mass, the temperature, the unperturbed density, and the polytropic index,[15] respectively. It is worth mentioning that the ratio of ha and mac2 can be regarded as the thermal parameter of effective mass increased from the rest mass of the particles.[11,13,16] The expression of ha implies that the magnitude of the thermal parameter depends on the relativity of the random motion as well as on plasmas density and polytropic index.

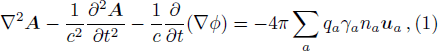
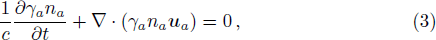
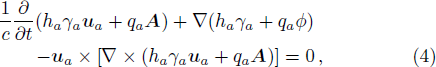
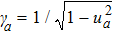
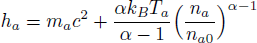
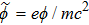
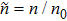
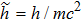
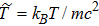
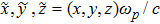
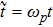
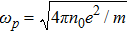
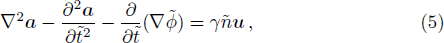
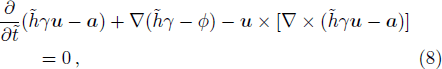
Equations (1)–(4) can be used for the investigation of linear or nonlinear physical phenomenon in laser- relativistic hot plasmas interaction. In the following, we neglect the motion of ions and drop the subscript a, i.e., all the variables represent the corresponding quantities of electrons. Introducing the following dimensionless variables a = eA/mc2, , , , , , and , where is the plasmas frequency, the dimensionless forms of Eqs. (1)–(4) can be written as

where q = –e (e = |e| is the charge amplitude of electron) is used.

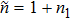
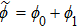
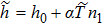
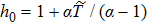
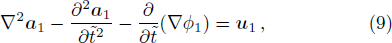
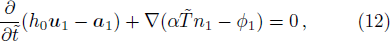
In present paper, we focus on discussing the temperature effects on the linear Langmuir and EM waves in the relativistic hot plasmas, and the nonlinear phenomenon will be discussed in the following papers. Accordingly, we write the physical quantities as a = a0 + a1, u = u0 + u1, , , , γ = 1 + u2/2, where . Therefore, the linearized forms of Eqs. (5)–(8) can be written as

where a0 = u0 = ϕ0 = 0 and a constant plasmas temperature are assumed. Since the EM wave is considered to be a disturbance, i.e., |a1| ≪ 1, the approximation γ ≈ 1 is used. It means that the relativistic effects induced by the oscillation motion of electrons are neglected.

3 Results and Discussion

In the following, we assume that the equation of state contrasts with the adiabatic equation,[13,16] i.e., the polytropic index α reduces to the adiabatic index.

The divergence of Eq. (12) gives

Considering ∇ · a = 0, and using Eqs. (10) and (11), Eq. (13) can be written as

Equation (14) is an equation of electron density perturbation. Letting , one can obtain a dispersion relation

In order to make the meaning of Eq. (15) more clear, we recover the dimension

where ω and k are the frequency and the wave number of Langmuir wave. Introducing an effective mass of electron as m* = h0m, where h0 can be regarded as the relativistic factor induced by the thermal motion of electrons, Eq. (16) can be written as

where is the electron adiabatic sound velocity in relativistic hot plasmas and Vse is the electron adiabatic sound velocity in nonrelativistic plasmas, is the plasmas frequency of relativistic hot plasmas. Considering h0 increased with the increase of the plasmas temperature, the electron adiabatic sound velocity and the plasmas frequency are reduced with the increase of the plasmas temperature in relativistic hot plasmas.

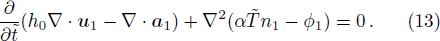
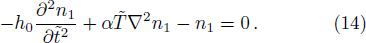
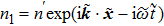
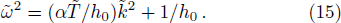
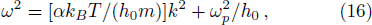
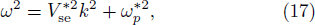
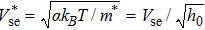
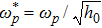
In warm plasmas, i.e., kBT/mc2 ≪ 1, Eq. (17) is reduced to

Equation (18) is the ordinary dispersion relation Langmuir waves.[17] In cold plasmas, i.e., T = 0, Eq. (17) is reduced to

Eq. (19) represents the Langmuir oscillation.[17]

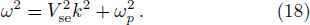
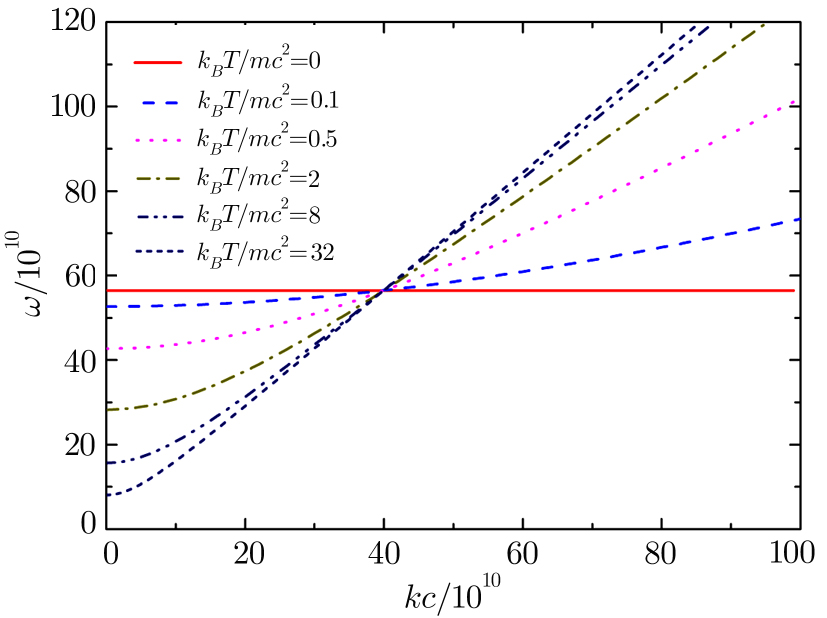Considering the Langmuir wave is a plane wave and the compression is one-dimensional, α = 3 is used in the numerical calculation. Figure 1 shows the relation of ω and kc under different plasmas temperature. The red solid curve is in the cold plasmas, i.e., T = 0, and it represents the dispersion relation of Langmuir oscillation. The other curves represent the dispersion relation at different temperature, i.e., kBT/mc2 = 0.1, 0.5, 2, 8, 32. Figure 1 shows that the relativistic temperature affects the dispersion relations of linear Langmuir waves obviously.

Fig. 1 (Color online) Dispersion plots for Langmuir wave with different plasmas temperature. The parameters n0 = 1014 cm−3 and α = 3 are presumed.

In the uniform plasmas, neglecting the variation of plasmas density, i.e., letting ϕ1 = n1 = 0, Eq. (12) gives

Considering h0 ˃ 1, Eq. (20) indicates that the oscillation velocity of electrons is slowed down in the relativistic hot plasmas. Therefore, the relativistic effect induced by electron oscillation can be neglected provided |a1|/h0 ≪ 1.

Substituting Eq. (20) into Eq. (9), it is easy to obtain the propagation equation of linear EM wave

Letting , the dispersion relation of linear EM wave is given by

Recovering the dimension of Eq. (22), the dispersion relation can be written as

where ω0 and k0 are the frequency and the wave number of EM wave. Equation (23) is the dispersion relation of linear EM wave in relativistic hot plasmas. In the nonrelativistic plasmas, i.e., kBT/mc2 ≪ 1, Eq. (23) is reduced to the ordinary dispersion relation of linear EM wave.[17]

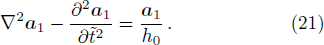
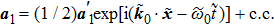
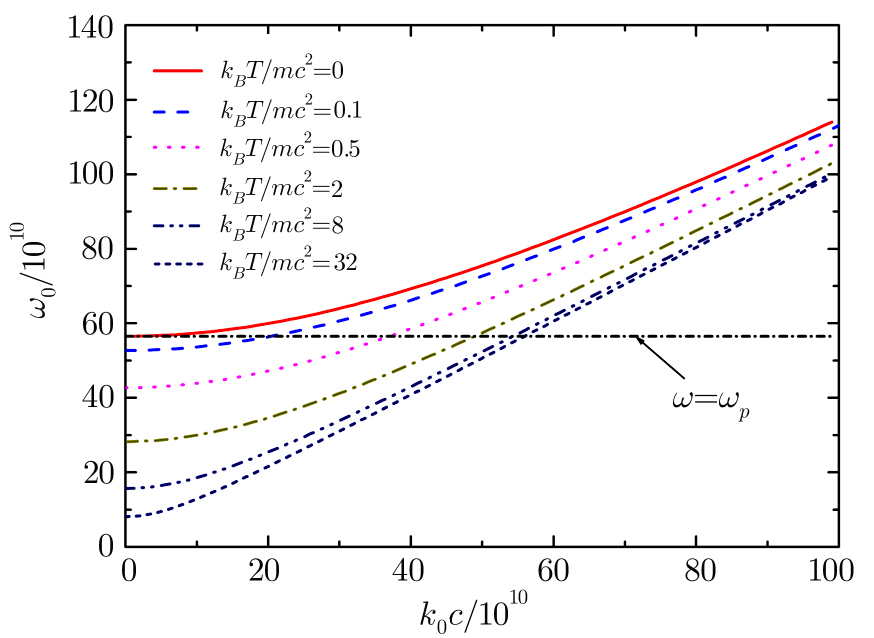Assuming a plane EM wave propagating in relativistic hot plasmas, the numerical result is shown in Fig. 2, where α = 3 is used in the numerical calculation. Figure 2 shows the relation of ω0 and k0c under different plasmas temperature. The red solid curve represents the dispersion relation of EM wave in cold plasmas, i.e., T = 0. The other curves represent the dispersion relation at different temperature, i.e., kBT/mc2 = 0.1, 0.5, 2, 8, 32 Figure 2 shows that the relativistic temperature also affects the dispersion relations of linear EM wave obviously.

Fig. 2 (Color online) Dispersion plots for linear EM wave with different plasmas temperature. The parameters n0 = 1014 cm−3 and α = 3 are presumed.

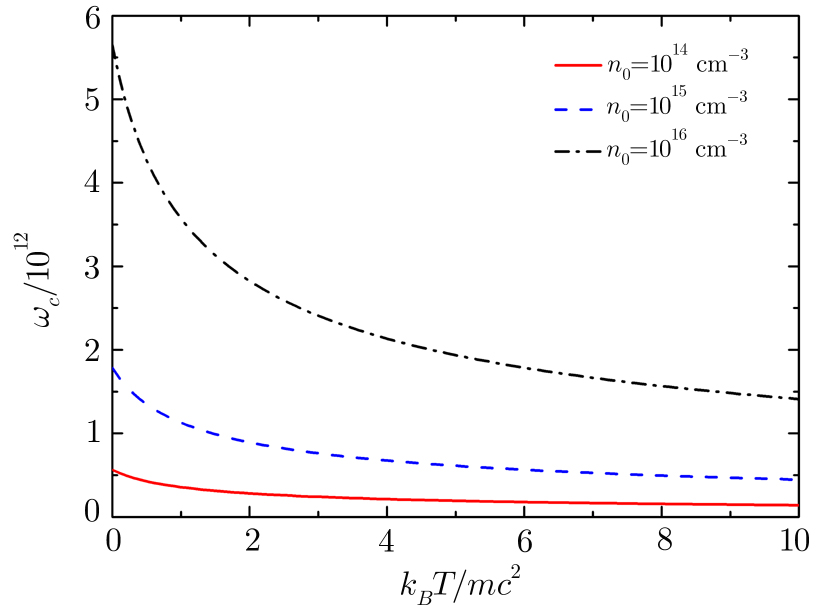
Letting k0 = 0, the critical frequency of EM wave propagating in plasmas can be obtained from Eq. (23)

Equation (24) hints that due to the increase of the electrons effective mass, the critical frequency decreased with the decrease of the plasmas frequency.

Figure 3 shows the variation of the critical frequency with the increase of plasmas temperature with different plasmas density. The red solid curve, blue dash curve, and the purple dash-dot curve represent the critical frequency in plasmas with n0 equal to 1014 cm−3, 1015 cm−3, and 1016 cm−3 respectively. Figure 3 shows that the critical frequency is decreased gradually with increase of the plasmas temperature in relativistic hot plasmas.

Fig. 3 (Color online) The variation of the critical frequency with the increase of plasmas temperature. The parameter α = 3 is presumed.
4 Conclusion

In relativistic hot plasmas, the increase of effective mass caused by the random motion of electron can trigger a series of influences on various physical processes, including linear and nonlinear processes. In the present paper, we have examined the influence of the effective mass increase on the linear Langmuir and the EM waves. The dispersion relations are obtained. Results show that when kBT/mc2 ˃ 1, the effective mass of electrons will be increased obviously. This increase not only depends on the relativity of the electrons’ random motion, but also depends on plasmas density and polytropic index. Furthermore, the effective mass increase will induce many other changes, such as the decrease of the plasmas frequency and the critical frequency, the reduction of the electron sound velocity and electrons’ oscillation velocity, and so on. Numerical results show that these variations have a strong impact on the propagation of linear Langmuir and the EM waves in relativistic hot plasmas.

Reference
[1] Andreev N. E. Gorbunov L. M. Mora P. et al. Phys. Plasmas 14 2007 083104
[2] Fox W. Fiksel G. Bhattacharjee A. et al. Phys. Rev. Lett. 111 2013 225002
[3] Marklund M. Shukla P. K. Rev. Mod. Phys. 78 2006 591
[4] Hu Qiang-Lin Xiao Gui-Lan Yu Xiao-Guang et al. Phys. Lett. A 377 2013 2594
[5] Barr H. C. Mason P. Parr D. M. Phys. Rev. Lett. 83 1999 1606
[6] Li G. Yan R. Ren C. et al. Phys. Rev. Lett. 100 2008 125002
[7] Li G. Yan R. Ren C. et al. Phys. Plasmas 18 2011 042703
[8] Tzeng K. C. Mori W. B. Phys. Rev. Lett. 81 1998 104
[9] Weng S. M. Liu M. Sheng Z. M. et al. Scientific Reports 6 2016 22150
[10] Lontano M. Bulanov S. Koga J. Phys. Plasmas 8 2001 5113
[11] Hu Qiang-Lin Chen Zhong-Ping Mahajan S. M. Phys. Lett. A 381 2017 869
[12] Li G. Mori W. B. Ren C. Phys. Rev. Lett. 110 2013 155002
[13] Lee N. C. Choi C. R. Phys. Plasmas 14 2007 022307
[14] Zhao Y. Zheng J. Chen M. et al. Phys. Plasmas 21 2014 112114
[15] Tribeche M. Boukhalfa S. Zerguini T. H. Phys. Plasmas 17 2010 082309
[16] Lee N. C. Phys. Plasmas 19 2012 082303
[17] Bittencourt J. A. Fundamentals of Plasma Physics Springer New York 2004