† Corresponding author. E-mail:
Project grant of Goverment of West Bengal, Department of Higher Education, Science and Technology and Biotechnology, File no:- ST/P/S&T/16G-19/2017, AH wishes to thank the Department of Mathematics, the University of Burdwan for the research facilities provided during the work. RB thanks IUCAA, Pune, India for providing Visiting Associateship
In this paper, we consider charged accelerating AdS black holes with nonlinear electromagnetic source. The metric chosen by us is of a regular black hole, which shows regular nature at poles and a conical effect, which corresponds to a cosmic string. In such a space time construction of the Lagrangian for a charged particle is done. Cyclic coordinates as well as the corresponding symmetry generators, i.e., the Killing vectors are found. Conservation laws corresponding to the symmetries are counted. Euler-Lagrange equations are found. The orbit is mainly taken to be a circular one and effective potential is found. The minimum velocity obtained by a particle to escape from innermost stable circular orbit is found. The value of this escape velocity is plotted with respect to the radius of the event horizon of the central black hole for different parametric values. The nature of the escape velocity is studied when the central object is working with gravitational force and charge simultaneously. Effective potential and effective force are also plotted. The range of radius of event horizon for which the effective force turns to be positive is found out. A pathway of future studies of accretion disc around such black holes is made.
Black Hole (BH hereafter) is the important prediction of General Relativity (GR hereafter). BHs are specified by the curved space-time geometry and bounded by the event horizons. Nowadays, the study of dynamics of particles around the BHs in the astrophysical background is found in many literature. Both the particles and photons in the vicinity of the BHs are highly attracted by the strong gravitational pull and as a result the accreted particles cause the gain of mass of the BHs. Again it is also possible that the BHs throw the particles away with high relativistic velocity due to angular momentum barrier. Furthermore the highly energised charged particles may also be escaped from their stable orbits around the BHs due to the collisions with other particles and are moved under the influence of the Lorentz force in the electromagnetic fields.
If the gravitational and electromagnetic fields are strong, the motions of the charged particles become, in general, chaotic and undetermined and so the corresponding orbits become unstable except the inner most stable circular orbit. The weak magnetic field does not affect the geometry of the concerned central BH but it may affect the motion of charged particles.[1–2] In the experimental point of view,[3–4] the magnetic field around the BHs occurs due to existence of plasma in the form of an accretion disc or a charged gas cloud[5–6] surrounding the BHs.
Mechanically, when the particles of a system collide with each other, the Center of Mass Energy (CME hereafter) occurs. Near the event horizon of a BH, the high CME is produced due to the collision of two particles. The mechanism of collision of two particles falling towards the Kerr BH has been proposed by Banados Silk and West (BSW mechanism hereafter).[7] Furthermore, the same authors have also shown that the CME, in the equatorial plane, may be highest for a fastly rotating BH. The BSW mechanism has been investigated for different BHs.[8–18] A general review of the mechanism of collision is viewed in Ref. [19]. The CME of the particles at the inner horizon of Kerr BH,[20] the CME of the collision of the particles around Kerr-Newmann BH,[21] near the horizon(s) of Kerr-Taub-NUT BH,[22] cylindrical BH,[23] Plebanski-Demianski BH,[24] Kerr-Newmann-Taub-NUT BH,[25] charged dilaton BH[26] have been studied.
The study of the dynamics of particles around the BHs in the presence of magnetic field has a special significance in recent time. The authors of some literatures[27–29] have investigated the motion of a charged particle near weakly magnetized Schwarzschild BH. In some other literatures[30–35] the authors have analyzed the chaotic motion of a charged particles around Kerr BH near magnetic field. Moreover in another paper[36] the authors have studied the circular motion of charged particles around Reissner-Nordstrom BH. Reference [37] has investigated the dynamics of charged particles around slowly rotating Kerr BH with magnetic field and also Ref. [38] has discussed about the dynamics of particles around Schwarzschild BH in the presence of quintessence and magnetic field. Recently, Ref. [39] has investigated the dynamics of particles around a regular BH surrounded by external magnetic field. Zhou et al.[40] has studied the geodesic structure of the Janis-Newman-Winicour space time. This space time contains a strong curvature naked singularity. Solving the geodesic equation and analysing the behavior of effective potential, they have shown all geodesic types of the test particles and photons. In 2009 Horava Lifshitz gravity was introduced. Timelike geodesic motion in Horava Lifshitz space time was studied in Ref. [41]. Differently energised particles’ motions are studied.
Motivated by the previous works, our objective in this paper is to apply the Euler-Lagrange equations of motion to study the properties of particle trajectories around the charged accelerating AdS (Anti-de-Sitter) BH surrounded by weak magnetic field.
This paper is organized as follows: in next section, we study a charged accelerating AdS BH metric with non-linear electromagnetic source and establish the Euler-Lagrange equation of motion radially. In Sec.
A charged accelerating AdS BHs can be expressed by the metric as[42–43]
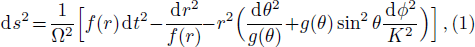
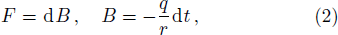
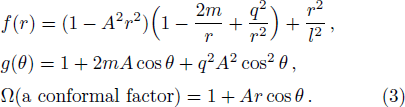
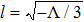
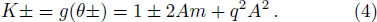
The Lagrangian of a charged particle of mass m and charge q in the absence of magnetic field is expressed as[29,38]
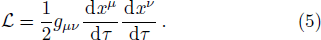
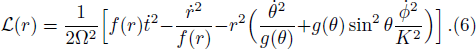

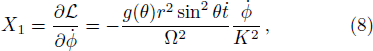
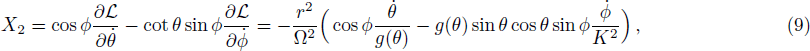
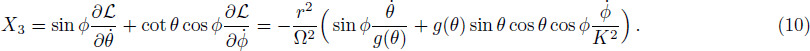

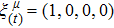
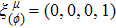
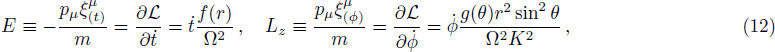
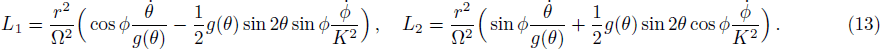
Here we apply the Euler-Lagrange equation of motion for r only and we obtain
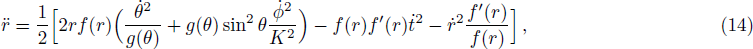
The constant of motion for that particle is given by Eq. (
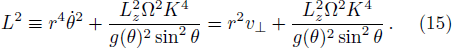
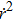
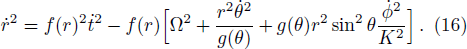
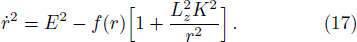
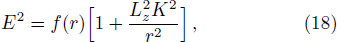
The critical azimuthal angular momentum of a particle that follows a particular orbit where the effective potential is extremum (i.e., maximum or minimum) and it is expressed as
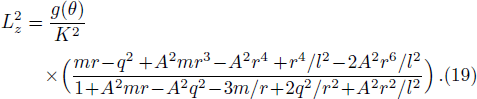
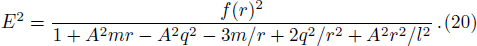
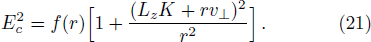
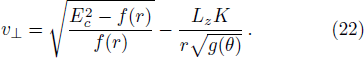
We now consider the case of weakly magnetized BH and investigate the motion of a charged particle having charge q in presence of magnetic field in the BH exterior. The general Killing vector equation is[44]

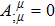

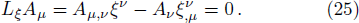
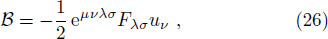
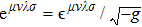
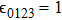
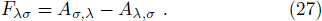
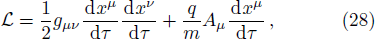
By employing the Lagrangian dynamics, we now examine the motion of a charged particle in the background of the BH (
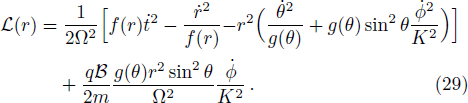
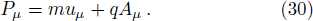
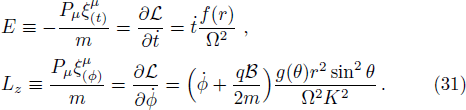
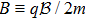
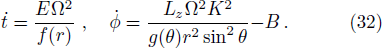
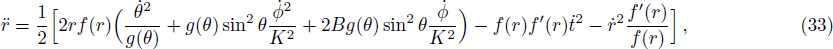
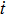
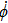
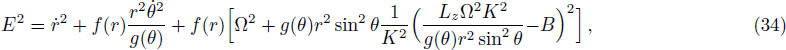
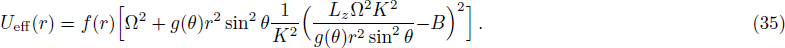
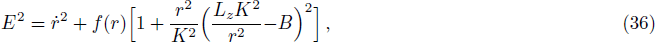
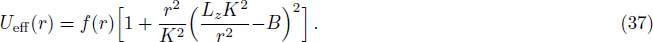
In order to integrate the dynamical equations, we need to make these equations dimensionless. We use the following transformation relations[38,46–47] as:
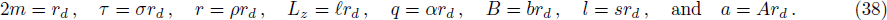
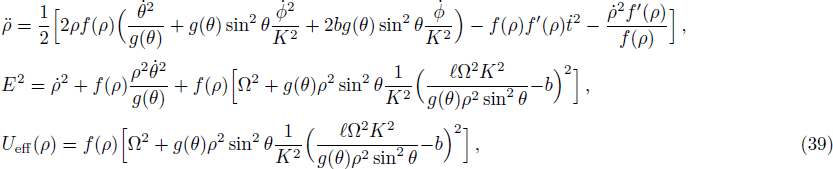
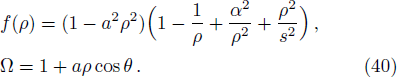
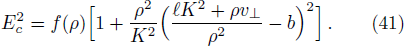
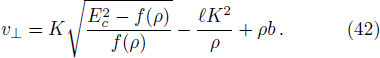
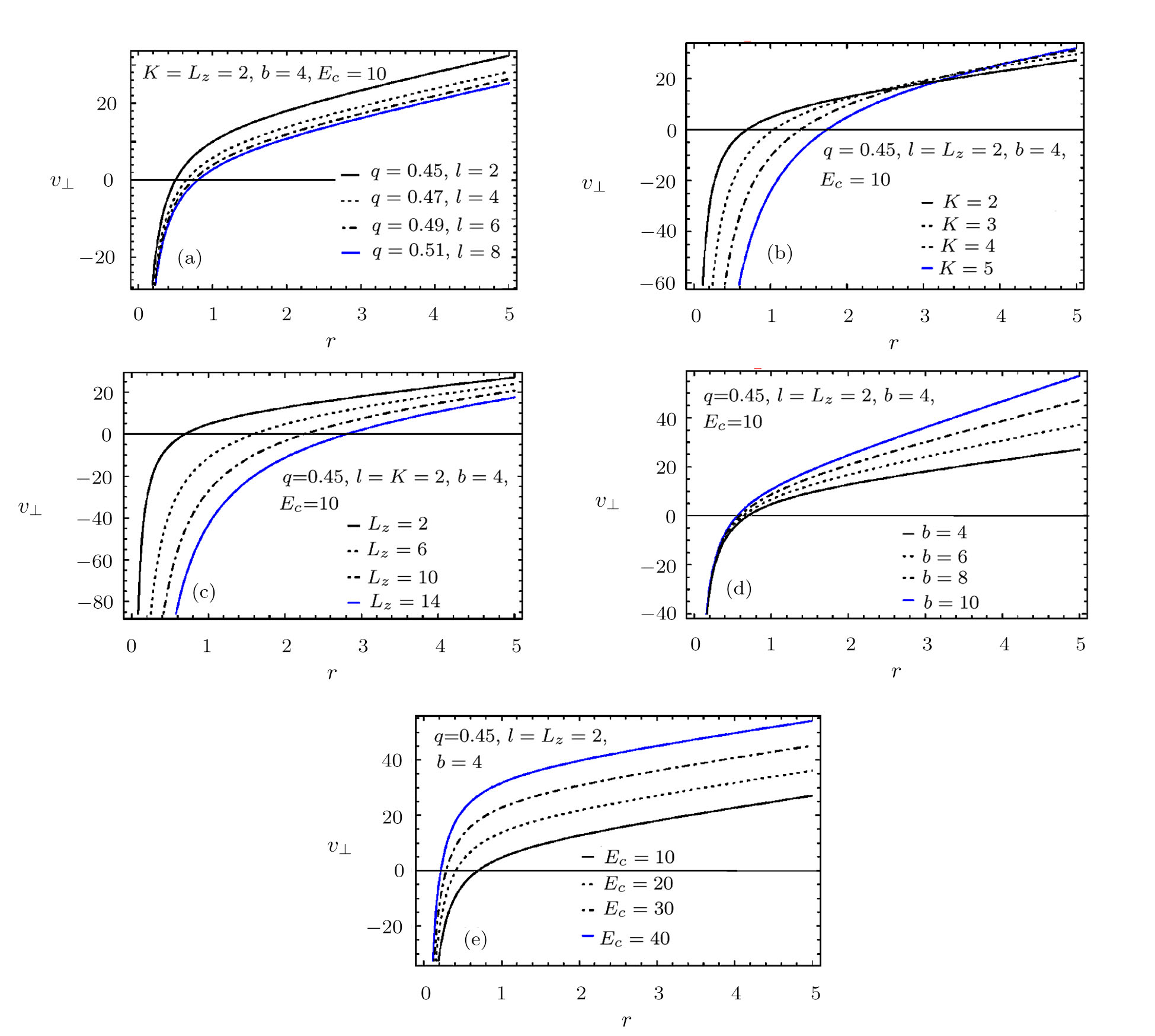
We have plotted the variation of escape velocity v⊥ of the particle with respect to the radius r of the BH for different values of q, l, K, b, Lz, and Ec in Figs.
In Fig.
In Fig.
We vary Lz keeping the parameters q, l, K, b, and Ec are unchanged in Fig.
Figures
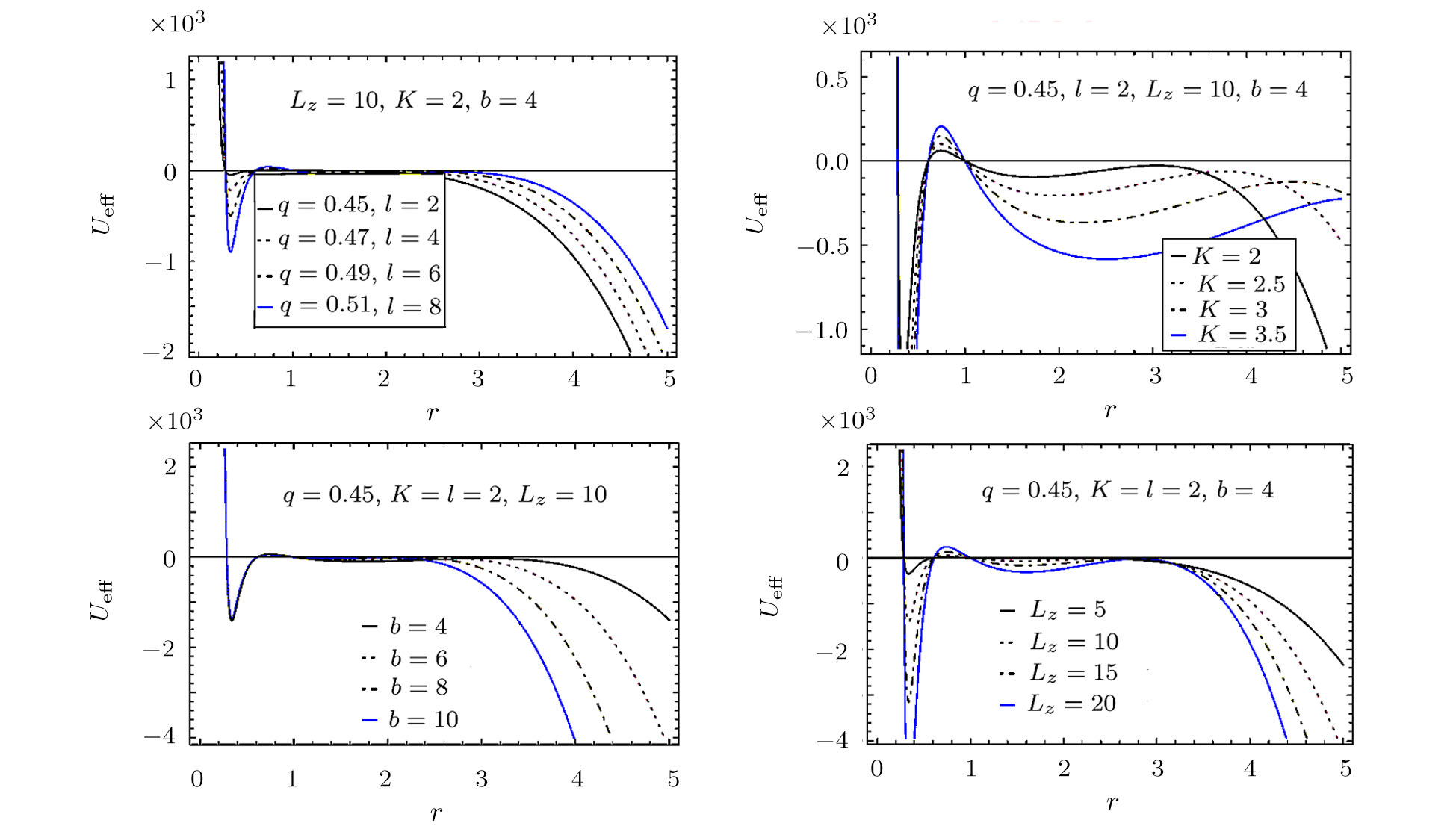
We have drawn the curves of effective potential Ueff of the particle corresponding to circular orbits with respect to radius r of BH for different values of q, l, K, b, and Lz in Figs.
In Fig.
The CME of the colliding particles is expressed as[39]
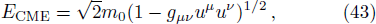
Applying Eq. (
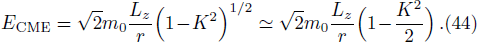
Applying Eq. (
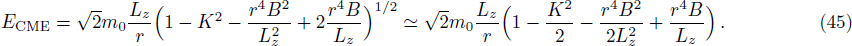
The effective force acting on the charged particles in the flat background normally measured by the Lorentz force but in the curved background it may be determined as follows
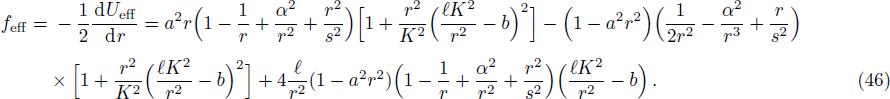
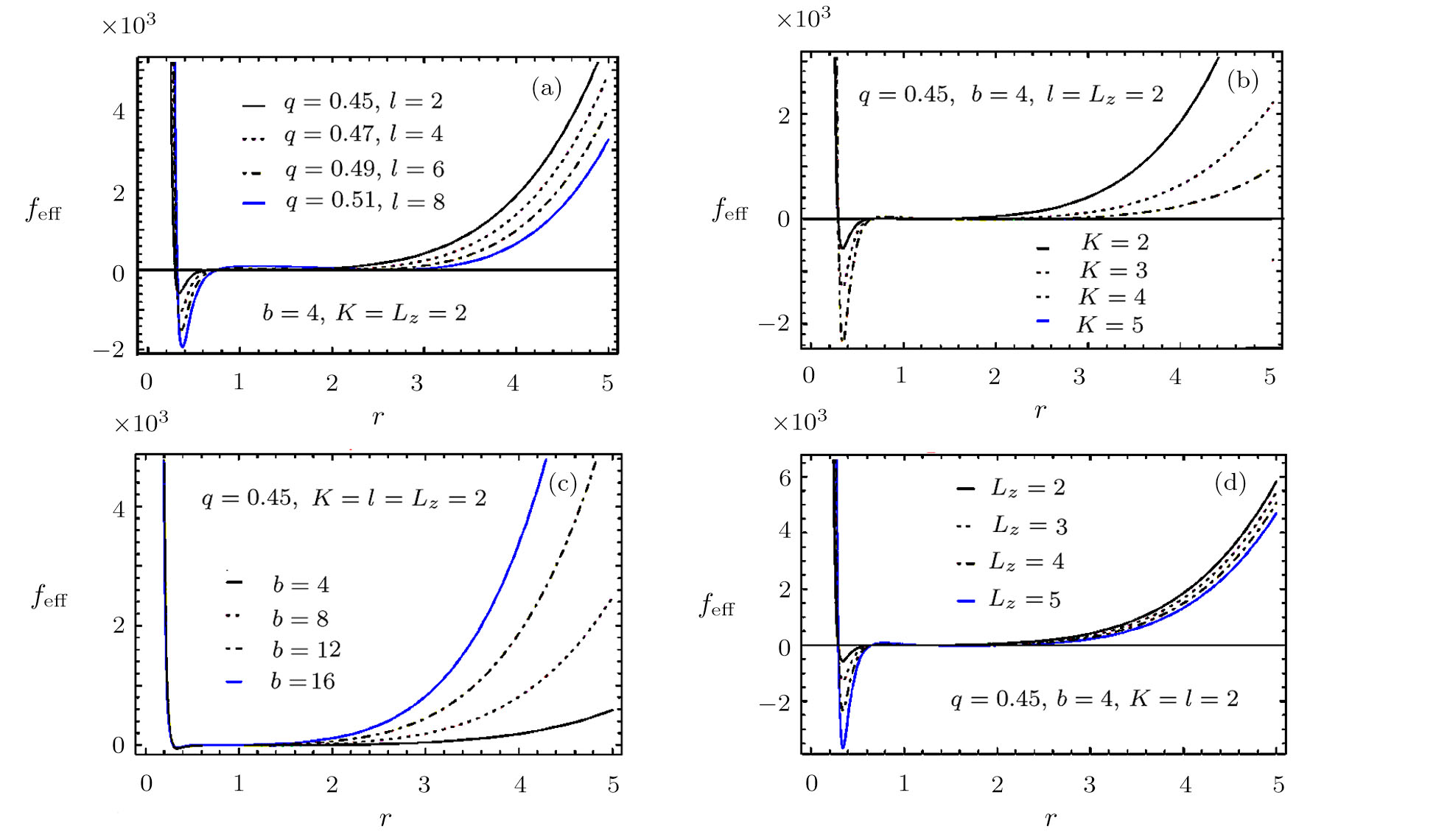
We have plotted here the graphs of effective force feff acting on the charged particle vs. the radius r of BH for different values of q, l, K, b, and Lz in Figs.
In our study, we investigate the dynamics of charged particles around charged accelerating AdS (anti-de-Sitter) black hole in the absence and presence of magnetic field by computing Euler-Lagrange equation of motion for radial component only. First of all we choose the charged accelerating AdS (anti-de Sitter) BH with non-linear electromagnetic source and analysis the effective potential, escape energy and therefore escape velocity in the absence and presence of magnetic field. We analysis the dependence of that physical quantities on the radius of BH graphically. We observe from Figs.
The variation of effective potential with radius of BH is studied in Figs.
Finally, we calculate the effective force acting on the charged particles in the curved background and examine its dependence on the radius of black bole graphically. We find there is a minimum negative value of effective force at very small radius of BH and then it reaches to zero, stay within few range of the radius for different values of charge and AdS radius (Fig.
We have studied the dynamics of both charged and chargeless particles. It is seen that more the charge, lower is the escape velocity. Dependency of escape velocity on K is somewhere different. For the quadratic nature of K, we see between two KLow and Khigh curves, there is a point rcrit where the system needs same escape velocity. In a nutshell, it is shown in this paper that as we shift from the Schwarzschild black hole and incorporate charge and magnetic field, the attracting nature increases and particles near to the central engine becomes more redshifted. If we compare our result with existing studies like[39] we observe their speculation is that the particle moving around such black holes should not feel the absence of the singularity of the central regular black hole. The effective part, according to them, must be the magnetic field present in the accretion disc. However, our study also indicates the same. Increment in magnetic field strength signifies that the rotating particle needs comparatively lesser value of escape velocity. Dynamics of a neutral and a charged particle around a Schwarzschild singularity embedded in quintessence universe has been studied in Ref. [38]. Energy conditions for stable orbits has been constructed. Their result has been more clearly stated in our work. In future, if the motion of a series of particles are been counted, then we will have an idea of accretion disc around such a regular black hole.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] |