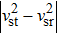† Corresponding author. E-mail:
In present paper, a static, spherically symmetric, anisotropic stellar object has been discussed by assuming a linear relationship between the matter density ρ and radial pressure pr. The interior solution is continuously matched with the exterior Schwarzschild vacuum solution at the junction interface. Various physical features viz. energy conditions, mass-radius relationship, stability are analyzed for our stellar model. By assigning some particular value to the arbitrary constants we have obtained a model of compact star of radius 6.7 km. and mass 1.148 M⊙, which is very close to the observational data of the compact star Her X-1 proposed by Rawls et al. [Rawls, et al., Astrophys. J.
In 1915 Einstein proposed General Theory of Relativity and the famous field equations. In the year 1916 Schwarzschild solved Einstein’s field equation for the interior of compact star in Hydrostatic equilibrium. After that have been investigated the relativistic astrophysical objects relating to static isotropic and anisotropic stellar type configuration in both theoretical and observational point of view. Exploration of astrophysical may provide an explanation to the queries about the fundamental laws of nature dealing with cosmic events and with the properties of matter under extreme conditions.
The study of compact object is always an interesting topic to the researchers. Theoretically there exist a number of comprehensive collections[1] of static, spherically symmetric solutions. These studies reveal that out of 127 published solutions only 16 of these satisfy all the physical conditions. According to Ruderman[2] it is found that the density of the core beyond the density ∼ 1015 gm/cc. provides the anisotropic nature of the stellar object i.e., the pressure can be decomposed into two parts: radial pressure pr and transverse pressure pt, where pt is in the orthogonal to pr. Anisotropy can be introduced by the existence of a solid stellar core or by the presence of a type 3A superfluid as indicated by Ref. [3], different kinds of phase transitions[4] or pion condensation.[5] According to Dev and Gleiser[6] it is revealed that pressure anisotropy affects the physical properties, stability and structure of stellar matter. The stability of stellar bodies is improved for positive measure of anisotropy when compared to configurations of isotropic stellar objects.[7] A natural question concerned to spherically symmetric relativistic static objects is to determine an upper bound on the compactness ratio m/r, where m is the ADM mass and r is the radius of the boundary of the static object. Reference [8] shows that a spherically symmetric isotropic object for which the energy density is non-increasing outwards satisfies the bound m/r ˂ 4/9. Since this bound was obtained for a class of isotropic fluid sphere violating the dominant energy condition, several researchers have worked in this area to find a sharp bound of maximum allowable ratio of mass to the radius for anisotropic spheres satisfying all the energy conditions. Sharp bounds on 2m/r for static spherical objects under a variety of assumptions on the eigenvalues of the Einstein tensor was obtained by Ref. [9]. Bounds on m/r for static objects with a positive cosmological constant was obtained by Ref. [10].
The consequence of mathematical modelling for the formation of compact object in cosmological context has great interest in recent time. It is very difficult to solve the Einstein’s field equation (EFE) due to its highly non-linear nature. Though it is unknown to us how the pressure related to the matter density inside a compact object, several researchers used linear and non-linear relation between pressure and matter density to find the solutions of the EFE. Reference [11] provided a new class of interior solution of a (2+1)-dimensional anisotropic star in Finch and Skea space-time corresponding to the BTZ black hole. The model is developed by considering the MIT bag model EOS and a particular ansatz for the metric function grr proposed by Ref. [12]. In the background of KB metric[13] proposed a new Singularity-free anisotropic strange quintessence star model by assuming a linear relationship between the matter density ρ and radial pressure pr. Reference [14] proposed a new model of dark energy star consisting of five zones, namely, the solid core of constant energy density, the thin shell between core and interior, an inhomogeneous interior region with anisotropic pressures, a thin shell, and the exterior vacuum region. Possibility of higher-dimensional anisotropic compact star was studied by Ref. [15]. Analytical models for quark stars assuming liner equation of state was studied by Ref. [16]. Reference [17] obtained an exact solution for a static anisotropic fluid sphere in static pseudo-spheroidal space-time. A model of compact relativistic body with anisotropic pressures in the presence of the electromagnetic field was studied by Ref. [18] by assuming a linear relationship between the pressure and density. Some recent works on compact star have been performed by Maurya et al.[19] and Banerjee et al.[20] by assuming specific mass function and conformal killing vector respectively. Reference [21] studied the behavior of static spherically symmetric relativistic objects with locally anisotropic matter distribution considering the Tolman VII form for the gravitational potential grr in curvature coordinates together with the linear relation between the energy density and the radial pressure. Reference [22] proposed a model of super dense star admitting conformal motion in presence of quintessence field by taking Ref. [23] ansatz motivated by accelerating phase of our present universe.
In spite of the execution of different modelling systems, we can apply mathematical modelling to get a relativistic solution of complicated astrophysical problem theoretically. Inspired by all of these earlier works, we obtain a new model of singularity free compact star by assuming a liner equation of state between the matter density and radial pressure and using a new expression for the metric potential grr.
The plan of investigation for this paper is as follows: In Sec.
The line element for a static spherically symmetry 4D space time has the form

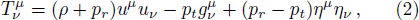
Assuming G = 1 = c the Einstein field equations are given by
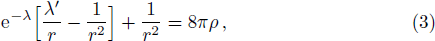
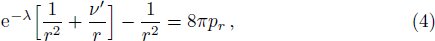
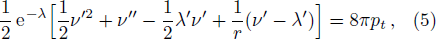
Introducing a new independent variable x and defining new functions y and Z so that
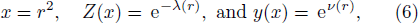


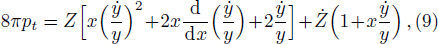
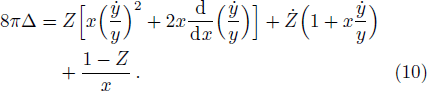
The field equations (
We seek solutions to the Einstein’s field equations (

Using Eqs. (
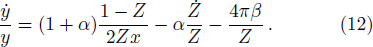
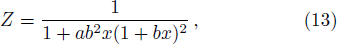
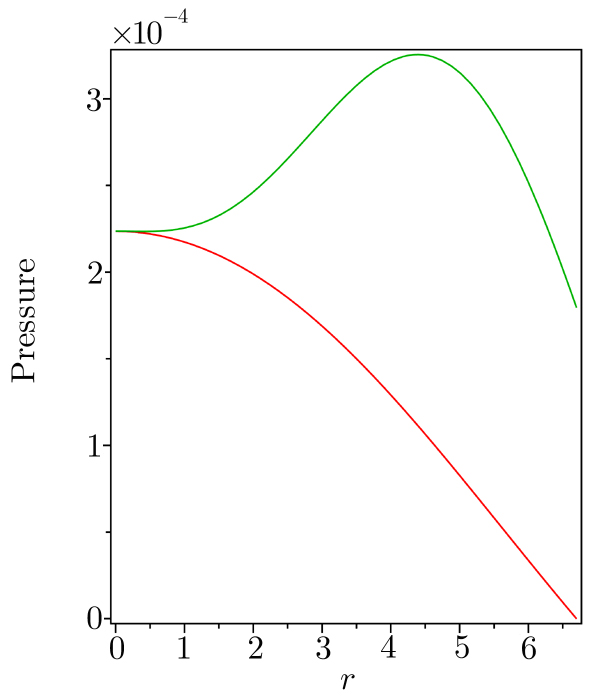
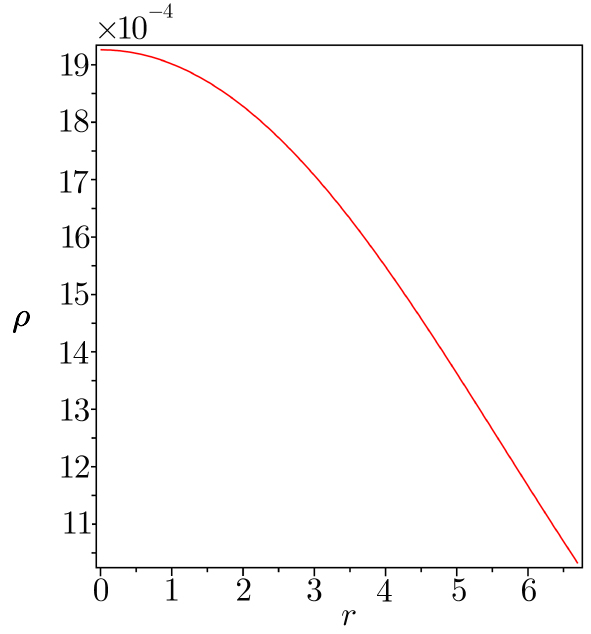 | Fig. 1 (Color online) Matter density is plotted against r inside the stellar interior by taking a = 915, b = 0.0042, α = 0.25, β = 0.000 258. |
Plugging Eq. (
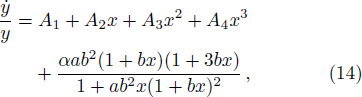
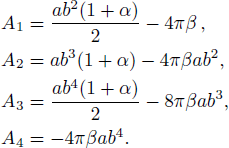
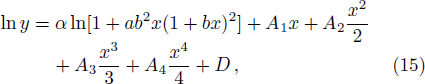
The matter density, radial and transverse pressure are obtained as,
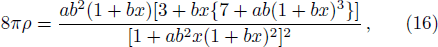



The interior spacetime for our proposed model continuously match to the Schwarzschild space time
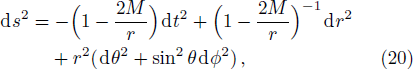
Using the continuity of eν and eλ across the boundary r = rΣ,
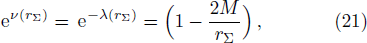

From Eqs. (
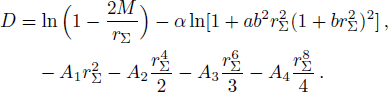
The central density and central pressure is obtained by,
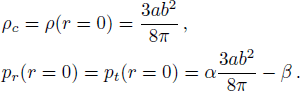
Differentiating Eqs. (
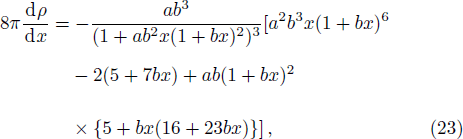

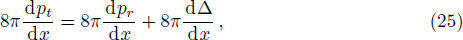
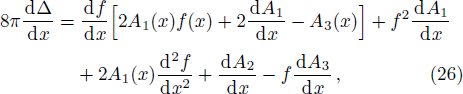
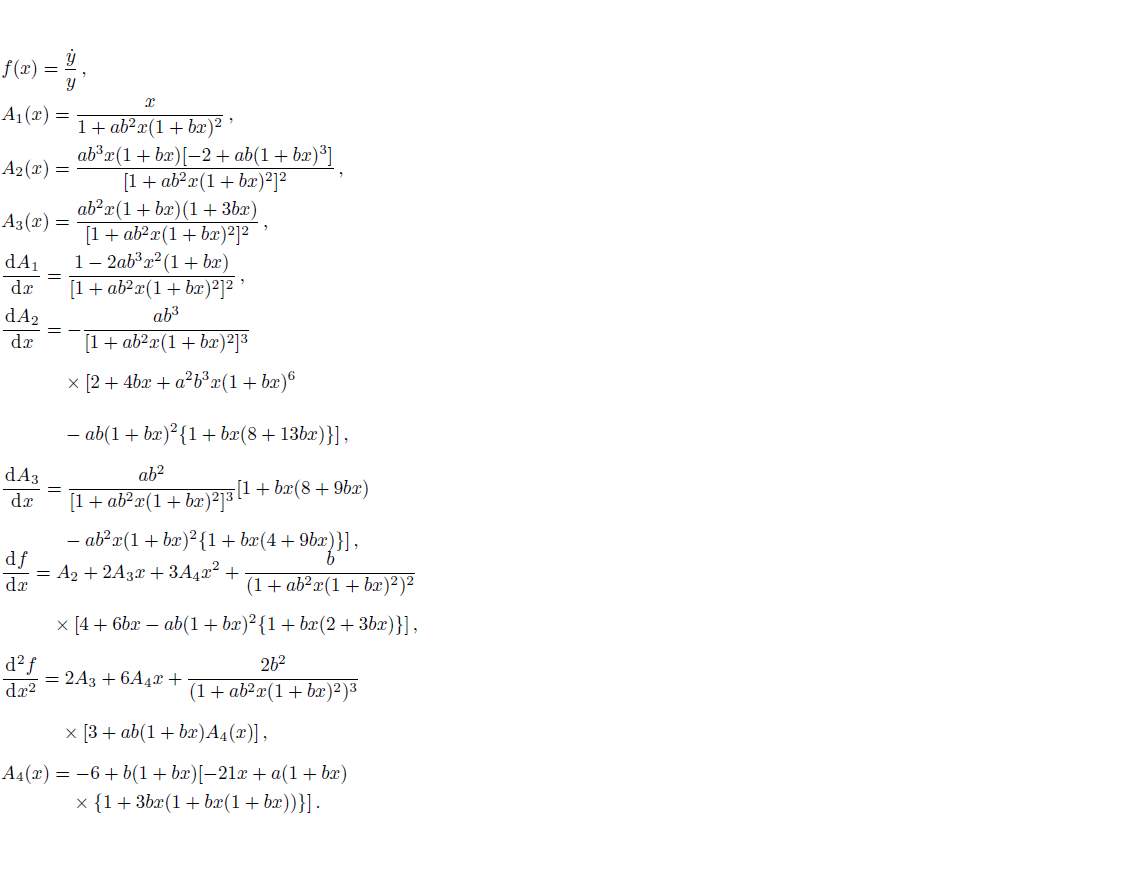
For our model eλ|r=0 = 1 and eν|r=0 = B, a positive constant. From Figs.
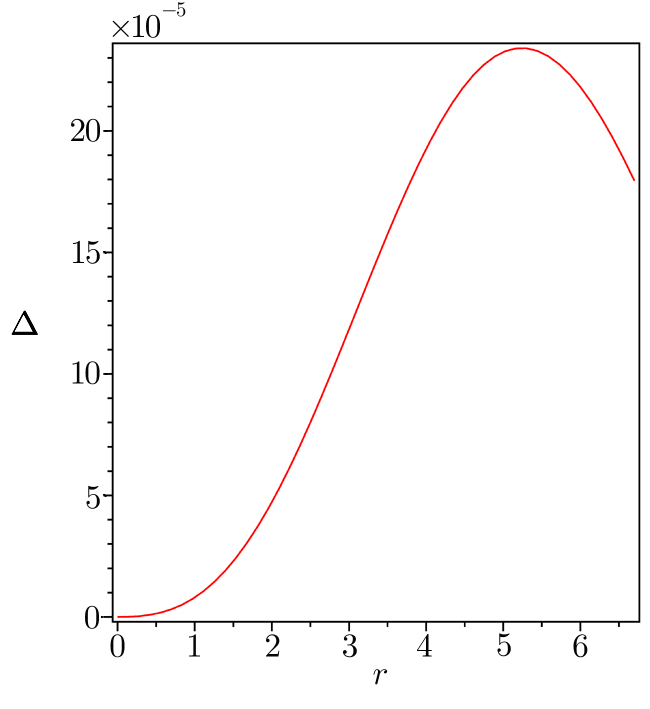 | Fig. 3 (Color online) Variation of anisotropic factor is plotted against r by taking the same values of the constant mentioned in Fig. |
In this section we check the different energy conditions for our proposed model. We know that for a model of compact star the energy conditions viz, null energy condition (NEC), weak energy condition (WEC), strong energy condition (SEC) and dominant energy condition (DEC) is satisfied if the following inequalities hold simultaneously:

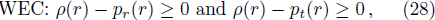
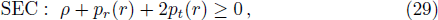
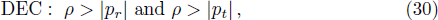
With the help of graphical representation in Fig.
The mass function for our model is obtained as,
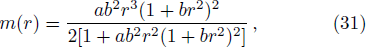
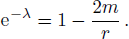
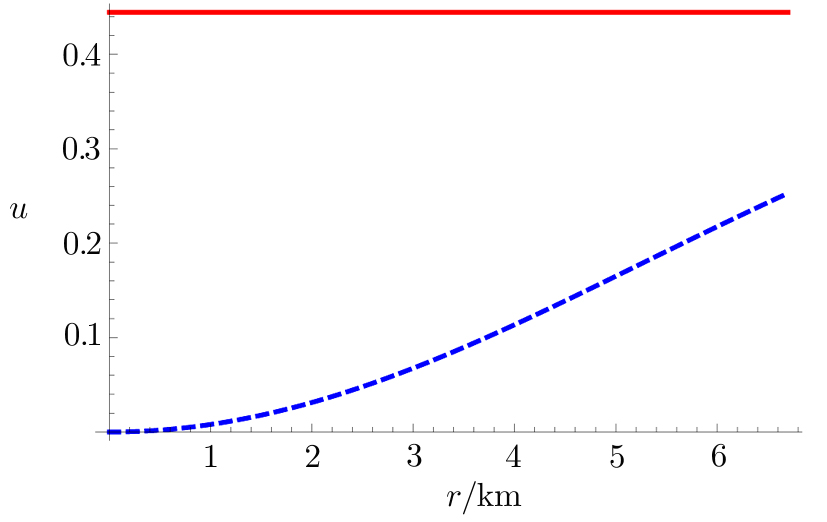
The compactness factor (u(r)) and surface redshift (zs(rΣ)) is obtained as,
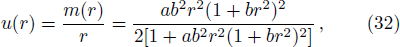
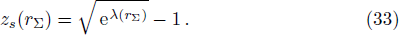
The profile of mass function is plotted against r in Fig.
 | Fig. 4 (Color online) Variation of mass function is plotted against r by taking the same values of the constant mentioned in Fig. |
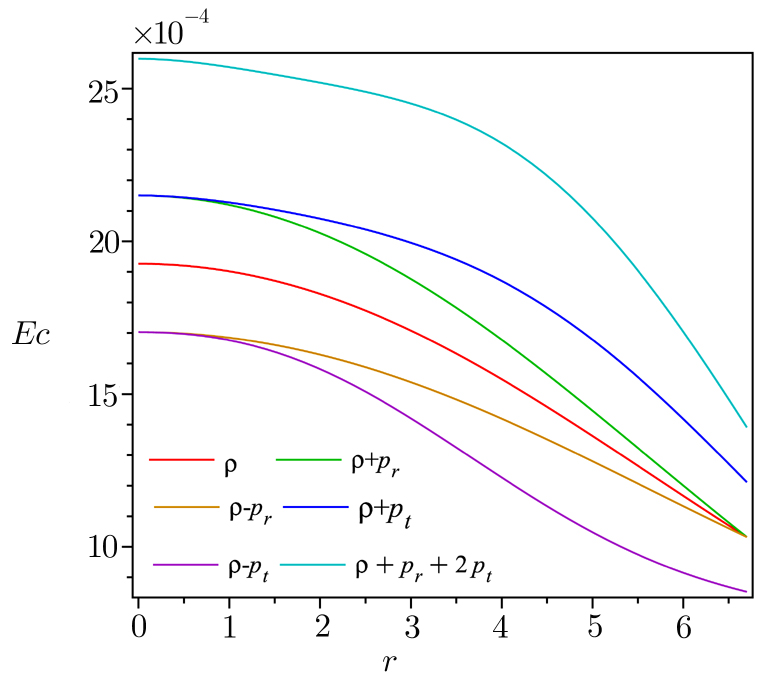 | Fig. 5 (Color online) The NEC, WEC, SEC and DEC are plotted against r for the compact star Her X-1 by taking the same values of the constant mentioned in Fig. |
In this article, the interior solution of a static, anisotropic compact star, governed by a linear equation of state pr = αρ − β with 0 ˂ α ˂ 1 and positive β, is matched with an exterior Schwarzschild vacuum solution with p = ρ = 0 at a junction surface Σ, with junction radius r = R. The metric coefficients are continuous at the junction surface S where r = R, but their derivatives may not be continuous at the junction. We shall now utilize Darmois-Israel[26–27] formalism to determine the surface stresses at the junction interface. The intrinsic surface stress energy tensor Sij at the junction surface Σ is obtained from the Lanczos equation[28–31] in the following form
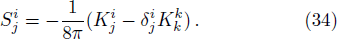
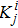
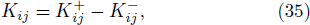
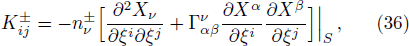
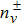
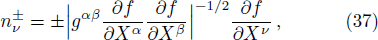
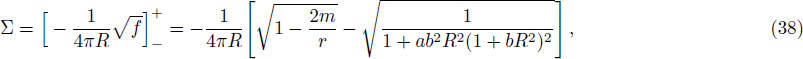
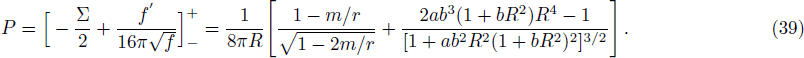
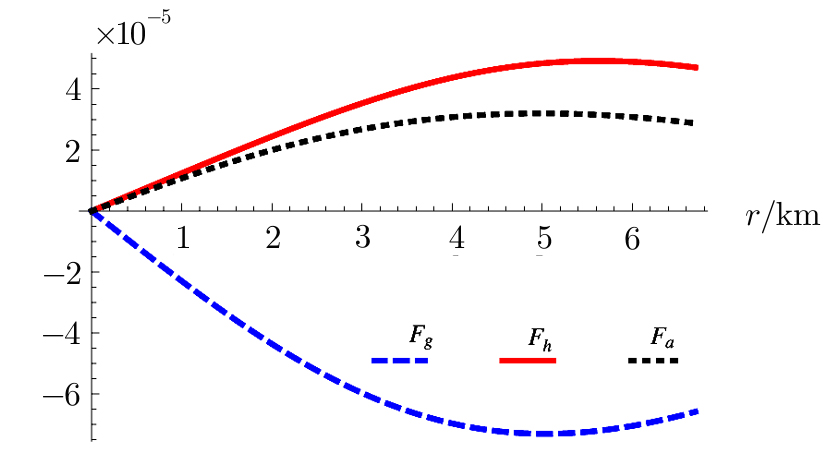
The generalized Tolman-Oppenheimer-Volkoff (TOV) equation for this system is described as
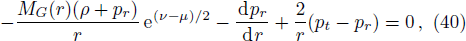
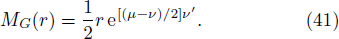
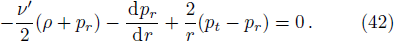
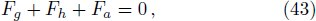
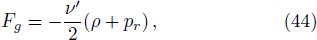


The profiles of the three different forces acting on the system are shown in Fig.
The adiabatic index Γ, provides the stability of a stellar configuration is given by,
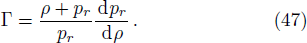
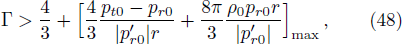
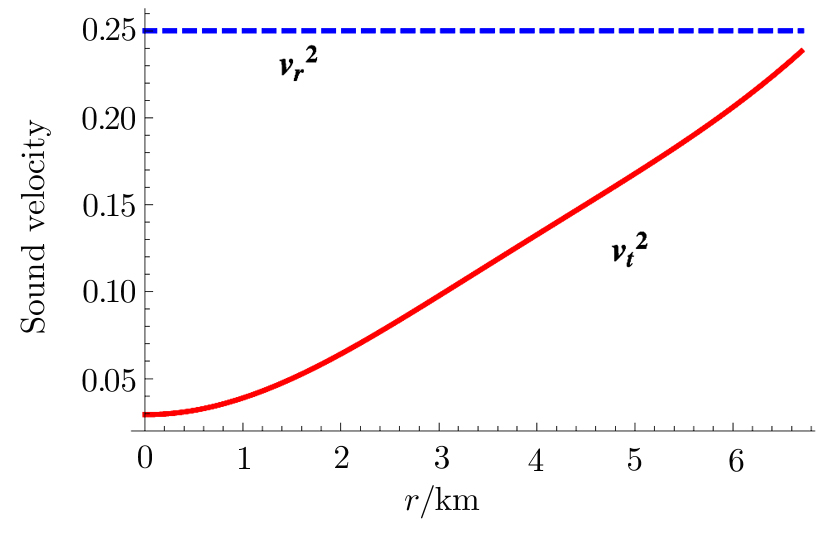
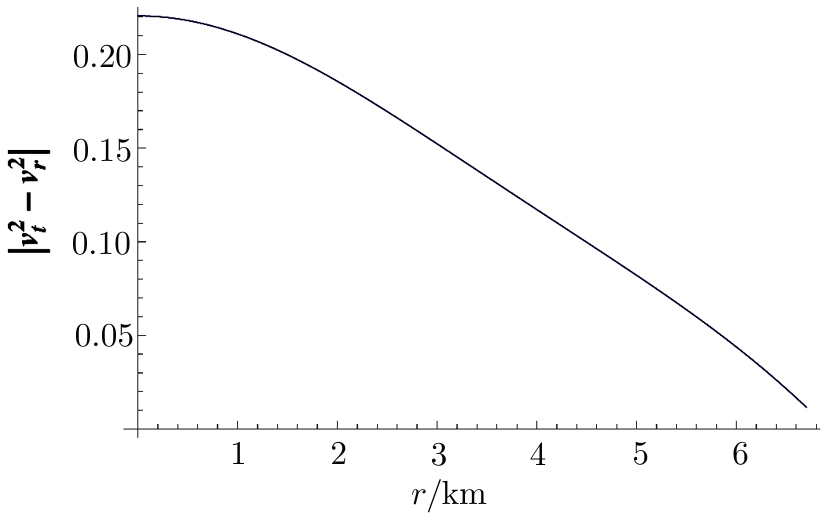
For a physically acceptable model the radial and transverse velocity of sound should lie in the range 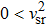
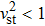
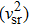
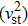
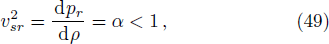
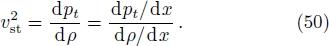
The expression for dpt/dx, dρ/dx are obtained in Eqs. (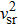
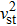
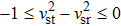


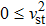
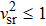
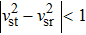
In the present study of mathematical model of relativistic anisotropic compact stellar model provides some interesting and physically acceptable solutions of the different metric potentials and the other physical parameters like density, pressure, mass etc. of the system.
(i) From Eqs. (
(ii) We have obtained the value of the constant D using matching condition.
(iii) From the graphical representation, it is found that the matter density, radial pressure (pr) and transverse pressure (pt) are all positive and monotonic decreasing function of r.
(iv) Taking a = 915, b = 0.0042, α = 0.25, β = 0.000 258 and using the conditions pr(r = rΣ) = 0, we obtain the radius of the star 6.7 km and mass of the star is obtained as 1.148 M⊙, which is very close to the observational data of compact star Her X-1 (Mass = 1.07 ± 0.36 M⊙).[35]
(v) Plugging G and c in the expression of ρ and pr we obtained the central density and central pressure as 2.6 × 1015 gm/cc. 2.72 × 1035 dyne/cm2, 1.39 × 1015 gm/cc., which indicates the physical stability of our model.
(vi) From graphical representation, it is found that the anisotropic factor Δ ˃ 0, i.e., anisotropic force is repulsive in nature, which implies that more compact object to be formed as discussed by Ref. [7]. Moreover it vanishes at the center of the star.
(vii) With the help of graphical representation, all energy conditions are satisfied by our proposed model.
(viii) By using the value of parameters we have obtained compactness factor = 0.253 and surface redshift zs = 0.423.
(ix) Figure
(x) The adiabatic index Γ ˃ 4/3 and the causality conditions are satisfied by our model, which ensures that our model is potentially stable.
Finally, we can say that all these results that we have obtained for our present investigation of compact stars are theoretically as well as physically admissible. So we can conclude that this model can be used for the description of ultra compact stars in future.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] |