† Corresponding author. E-mail:
Supported by the National Natural Science Foundation of China under Grant No. 11365006 and the Natural Science Foundation of Guizhou Province under Grant No. QKHLHZ[2015]7767
Nonclassicality is an essential but still open question in quantum mechanics. Here, utilizing the maximum value of quantum Fisher information, we suggest a new version of the nonclassical criterion for SU(2) generator realized by two bosonic modes. As an application of the criterion, the system of two coupled nonlinear nanomechanical resonators is considered. And the nonclassicality of the phonon state in the dynamical evolution is explored. The system has a dynamical phase transition from the tunnelling phase to the self-trapping phase by tuning the coupling strength. It is found that for the tunnelling phase, the phonon state is nonclassical in the full time evolution. And for the self-trapping phase, the evolved phonon state is still nonclassical in the full time with a relatively large coupling strength, while it is nonclassical i n the most of time (but not all) with a small coupling strength. Quantum coherence has distinct different behaviors in the two phases.
The nonclassicality is a basic feature of a quantum-mechanical system.[1–2] It is believed that the nonclassicality, as a resource for quantum information process, may be used to accomplish a task better than its classical counterpart. The well-known example is the quantum teleportation[3] achieved with the aid of the entangled state. Probing the nonclassicality of a given quantum state should be the first step to implement it as the resource of information processing. Lots of criteria have been proposed to detect the nonclassicality, such as the Mandel Q-factor,[4] the negativity of P-function,[5] and Wigner function,[6] the standard entanglement potentials,[7–8] the characteristic function,[9] just to mention a few.
At present, the nonclassicality of a quantum state is still an open question. There does not exist a simple and unified nonclassical criterion, just like the concurrence entanglement for two qubits, because a single criterion can only detect some quantum facets. For example, the Wigner function of a squeezed coherent state is positive, even it is generally considered as a nonclassical state.[10] And the photon statistics of the Schrödinger’ cat state is Poissonian, but its Wigner function has the negative part.
In parallel to the nonclassicality, quantum Fisher information (QFI),[11] which describes the sensitivity of a state in terms of parameter change, plays a central role in quantum parameter estimation and quantum metrology. According to quantum Cramér-Rao inequality,[12] quantum Fisher information determines the upper bound of the parameter estimation precision.[13] Moreover, QFI is also related to entanglement,[14] squeezing,[15–16] quantum phase transition,[17] and quantum illumination.[18] Recently, a nonclassicality criterion of a quantum state based on QFI has been suggested.[19] The main idea behind Ref. [19] is that for an imaginary interferometer, a nonclassical state should produce a better resolution than a coherent state (with the same mean particle number).
At the same time, with the advance of the nano-technology, high quality-factor nanomechanical resonators[20–21] become a key element of precise measurement, such as detection of spin,[22] mass,[23] displacement,[24] etc. More importantly, nanomechanical resonators with the GHz resonance frequency are suitable candidates for testing the quantum mechanics in the mesoscopic scale. However, in the GHz frequency regime, the nonlinear (or anharmonic) behavior of nanomechanical resonators must be considered,[25] which has a nontrivial effect and provides new possibility realizing quantum coherent device.[26–27]
In this paper, based on the maximum value of quantum Fisher information, a new version of the nonclassical criterion for SU(2) generator with the two bosonic modes realization is proposed. This new criterion is exploited to explore the nonclassicality of two coupled nonlinear nanomechanical resonators in the dynamical evolution. The resonators have two dynamical phases:[28] the tunnelling phase and the self-trapping phase. It is demonstrated that in the tunnelling phase, the phonon state is nonclassical in the full time evolution. For the self-trapping phase, the evolved phonon state is still nonclassical all the time with a relatively large coupling strength, while it is nonclassical in the most of time (but not all) with a small coupling strength. And it is found that quantum coherence has distinct different behaviors in the two phases.
The structure of this paper is as follows. Based on the maximum value of the QFI, in Sec.
Coherent state, defined as the eigenstate of the annihilation operator, is generally considered as an important class of quantum state. In this paper, we will explore the nonclassicality in the frame of quantum metrology. Usually, it is believed that the metrological resolution beyond the coherent state is the quantum effect. That is, a given state is nonclassical if it can provide a better resolution than coherent states with the same mean particle number.
In quantum metrology, the unitary transformation, as the most common situation, is described as
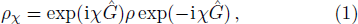
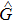
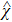
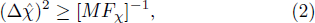
Specifically, let us focus on a two-mode SU(2) generator
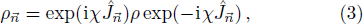
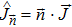
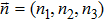
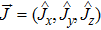
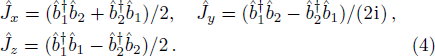
The annihilation(creation) operators 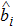
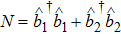
It should be stressed that it is not necessary to have a real rotation acting on ρ. The role of this fictitious transformation Eq. (
For a classical state ρclass = ∫ d2αPclass(α)|α〉〈α|, making use of the fact that the QFI is convex, it is easy to obtain that

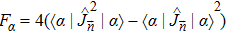
Introducing the operator 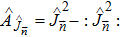
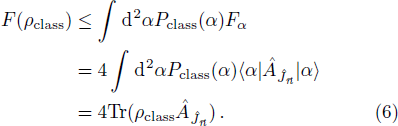
The violation of Eq. (
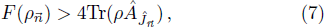
The nonclassical criterion Eq. (
According to Eq. (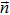
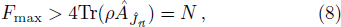
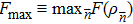
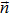
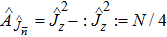
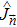
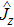
Now, the remaining question is how to compute the maximum value of the QFI Fmax. For a pure state, which is closely relevant to the phonon state in Sec. 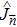
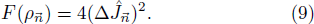
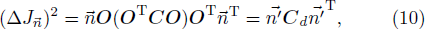
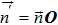
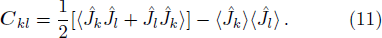
To provide further evidence on the advantage of choosing Fmax for Eq. (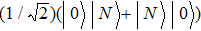
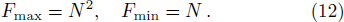
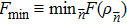
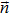
Two coupled nonlinear nanomechanical resonators have the Hamiltonian in the following form[37] (ħ = 1)
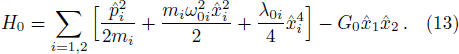
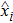
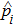
In the rotating frame with respect to ω01, the original Hamiltonian is changed into[38]
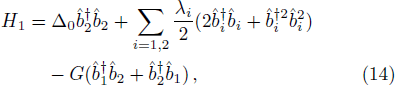
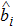
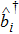
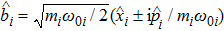
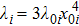
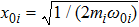
In Eq. (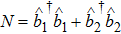
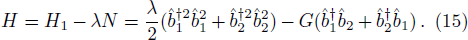
Taking the following facts into consideration that (i) the decoherent time of the nanomechanical resonators is relatively long with a very high quality-factor, and (ii) our new version of the nonclassicality criterion is only valid for the unitary evolution, the effect of the dissipation of the nanomechanical resonators will be omitted in this paper. The dynamics of the system is determined by the Schrödinger equation
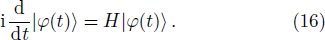
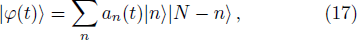
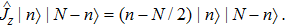
The Hamiltonian Eq. (
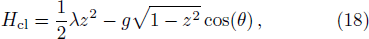

It is well-known that the system has two dynamical phases: a tunnelling phase and a self-trapping phase. For an initial state determined by (θi, zi), the critical value gcr separating the two dynamical phases is given as[43] 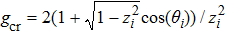
Although the form of Hamiltonian Eq. (
In this section, we firstly investigate the nonclassical property of the two resonators based on the maximum value of the QFI, and then study the quantum coherence of the system.
Here our criterion Eq. (
According to Eq. (
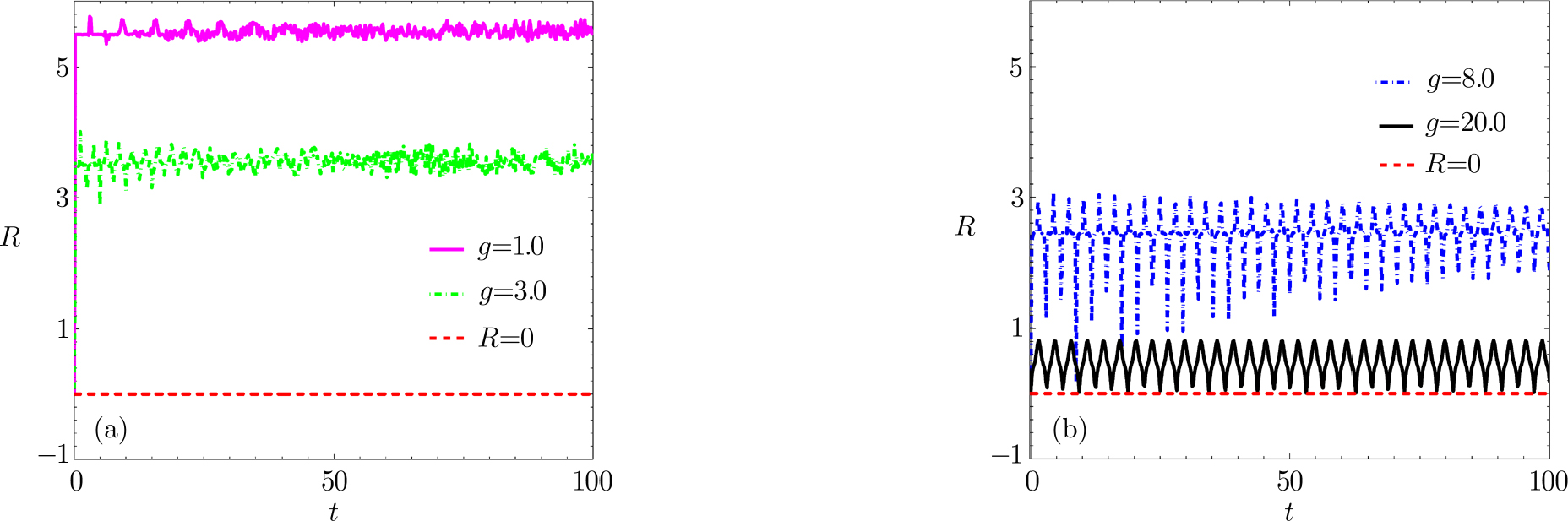
Figure
More interestingly, Fig.
These results can be understood as follows. In the tunnelling phase with g < gcr = 2.0, the tunnelling term in Eq. (
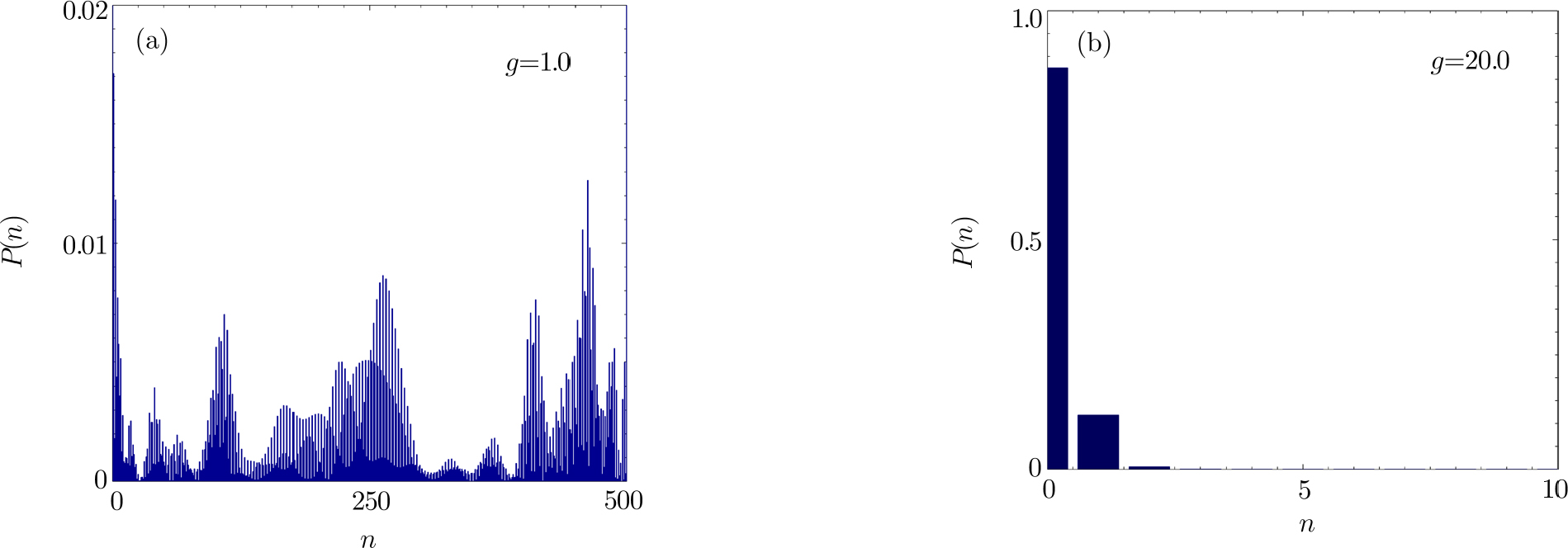
To further gain some intuitive picture of these results, the probability distribution P(n) = |an(t)|2 at a fixed representative time is shown in Fig.
The quantum coherence of the two nanomechanical resonators has been investigated in Ref. [38], which is quantified by the mean fringe visibility 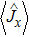
The relative entropy coherence of the phonon state |φ(t)〉 is given as[47–48]
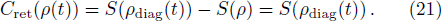
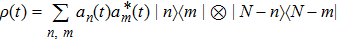
The other kind of coherence, so-called l1-norm is defined as[49]
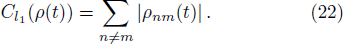
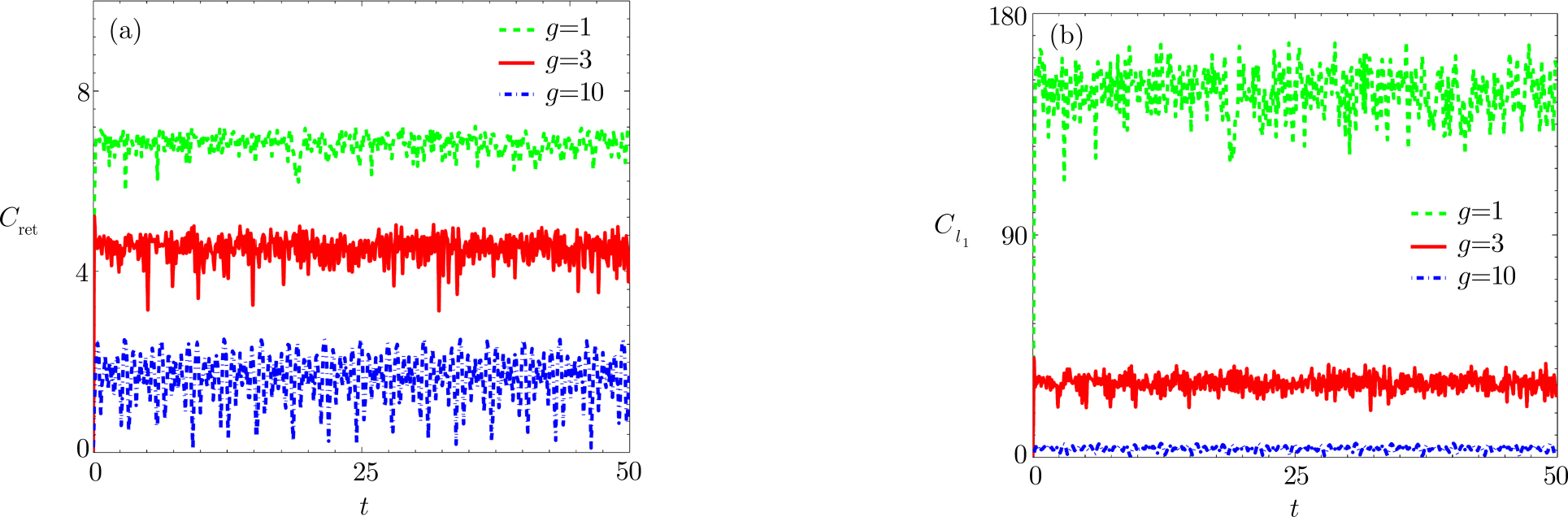
Figure
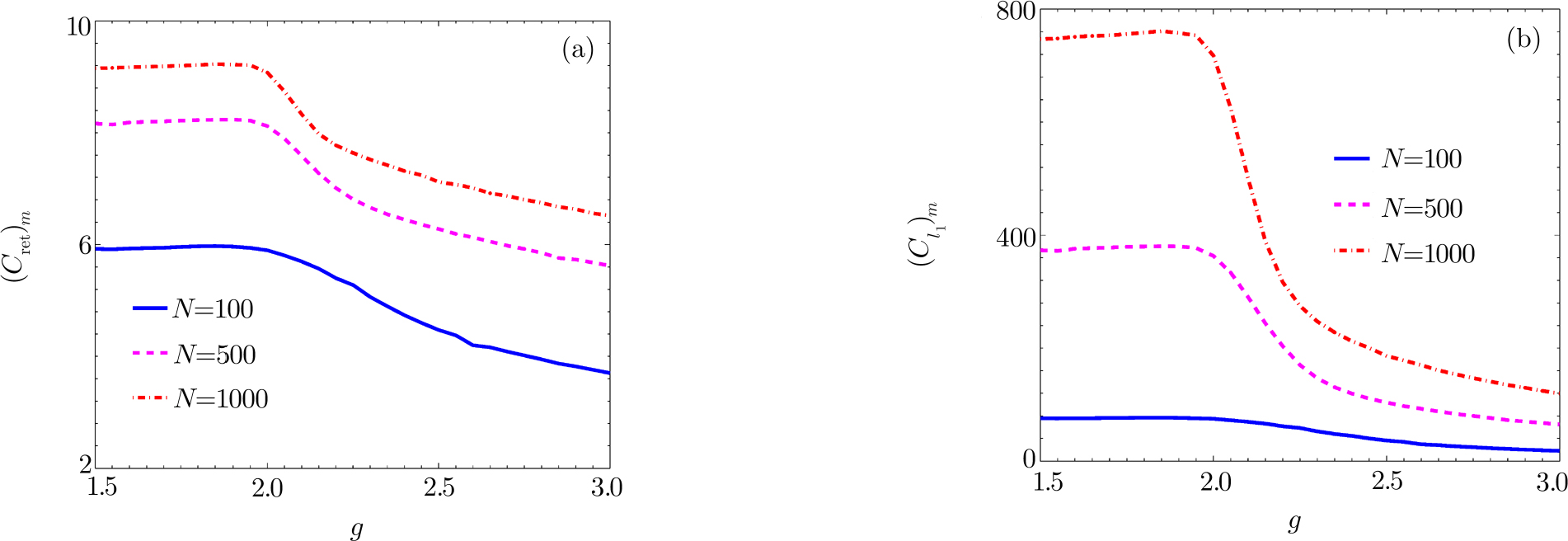
To well describe the property of the nanomechanical resonators, we also consider the time-averaged values of two kinds of quantum coherence
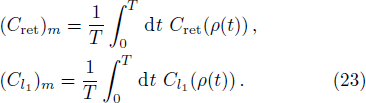
Figure
In this paper, making use of the maximum value of the quantum Fisher information, we propose a new edition of the nonclassical criterion for the SU(2) generator realized by two bosonic modes. As an example, we apply our nonclassical criterion to the system of two coupled nonlinear nanomechanical resonators. The phonon state of the resonators has two dynamical phases: a tunnelling phase and a self-trapping phase. In the case of omitting the phononic dissipation, we find that for the tunnelling phase, the phonon state is nonclassical in the full time evolution. For the self-trapping phase, the evolved phonon state is still nonclassical all the time with a relatively large coupling strength, while it is nonclassical in the most of time (but not all) with a small coupling strength. And we also show that quantum coherence has distinct different behaviors in these two phases.
In future, it is an interesting topic to explore the effect of the phononic dissipation on the nonclassicality. More importantly, extending our witness as a measure for the nonclassicality based on the quantum Fisher information should be more useful.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] |