† Corresponding author. E-mail:
The one-dimensional Dirac particle for equal scalar and vector asymmetric q-parameter hyperbolic Pöschl-Teller potential (qHPT) is solved in terms of hypergeometric functions. The scattering and bound states are obtained by using the properties of the equation of continuity of the wave functions. We calculat in details the transmission and reflection coefficients.
The scattering and bound states in relativistic and non-relativistic quantum mechanics with external potentials have received attention from theorist in recent years[1–3] and have assisted in the description of the behaviour of particles, atoms, and molecules in Physics. They find their applications in atomic and molecular Physics[4–17] and in condensed matter physics.[18–26] The Dirac equation covers the anti-particle scattering as well as the particle scattering. The scattering states have continuum wave functions and its energy is within the neighbourhood of E ≥ 0 whereas the bound states with normalizable wave functions have energy E < 0. For a free Dirac particle, there exist energy gaps E ≤ |m| (where m is the mass of the particle) that separate the positive and negative energy continuum states. The positive states correspond to the particle states and the negative energy states describe the anti-particle states. The energy gap becomes distorted on the introduction of a potential V(r) and bound states now occur between E = −m and E = m, which can be described as the band gap energy in condensed matter Physics.
The relativistic and non-relativistic symmetries have been investigated under a wide range of potentials.[27–31] The Pöschl-Teller potential (PTP) in this regards has attracted the interest of many researchers in recent years owing to its applications in molecular and nuclear physics.[32–40] The relativistic solutions to the PTP have been obtained with the Duffin-Kemmer-Petiau,[1] Dirac,[32–34] Klein-Gordon,[35] and the Schrödinger wave equation.[36–37] For instance, Jia et al.[32] obtained the analytical solutions of the Dirac equation with the generalized Pöschl-Teller potential including the pseudo-centrifugal term while the relativistic symmetries with the trigonometric Pöschl-Teller potential plus Coulomb-like tensor interaction have also been obtained by Falaye and Ikhdair.[33] The bound and scattering state of the q-hyperbolic Pöschl-Teller (qHPT) has also been investigated for the Duffin-Kemmer-Petiau equation.[1] The scattering and bound states of a spinless Klein-Gordon equation with the generalized PTP has been studied[35] and the author calculated the eigenvalues, normalized wave functions, and the scattering phase shift respectively. In Ref. [34] the spin symmetry for the Dirac equation with modified qHPT in D dimensions were also solved and the relativistic energy spectrum was obtained by using the Nikiforov-Uvarov method. Also in Ref. [36] the bound state solutions of the Schröinger wave equation with the generalized Pöschl-Teller potential in D spatial dimension was obtained. The Pöschl-Teller potential is a typical diatomic molecular potential that has related applications in relativistic and nonrelativistic cases for real diatomic molecules.[37–38] For instance, Jia et al.[37] used the Improved Pöschl-Teller potential energy model in fitting the experimental RKR potential curves over a large range of internuclear distances for six molecules and was found to fit better than the Morse potential. Other molecular potential models of interest that have been improved upon in this regard include the Tietz,[39] Manning-Rosen,[40–41] and the Rosen-Morse.[42] the Dirac equation has been used to study the deformation of nuclei,[38] which plays a major role in understanding the deformation potentials in quantum dots (QDs).[38–40] A study made by some authors have shown that in the absence of mass term, the Dirac equation can be used to obtain the bound states of confined graphene QDs.[18–26]
Motivated by the diverse applications of the PTP model in condensed matter and molecular Physics, the scattering and bound states solution of the qHPT potential will be studied using the Dirac equation.
Accordingly, the q-parameter hyperbolic Pöschl-Teller potential (qHPT) is given by[1]
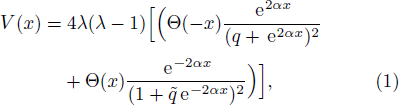

The organization of this paper consists of four sections: In Sec.
The basic theories and equations governing the Dirac particles are given in Refs. [27–34].
Let us recall that the Dirac equation with the scalar potential S(x) and vector potential V(x) in one-dimensional is given by[27]
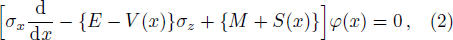
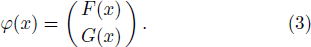
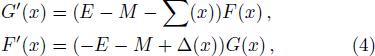
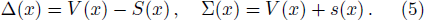
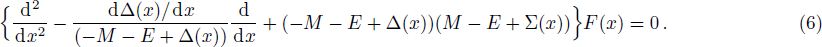
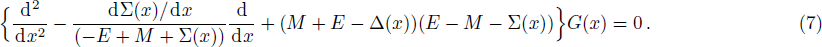
First of all, let us consider the case for which Σ(x) = Cp = constant so that Δ(x) has the asymmetric qHPT potential (V(x)) given in Eq. (
In solving for the scattering states, we study the wave functions for x < 0 and then the Dirac equation with the q-parameter hyperbolic Pöschl-Teller Potential (qHPT) is given by inserting Eq. (
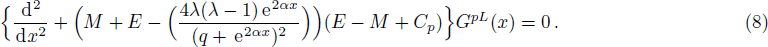
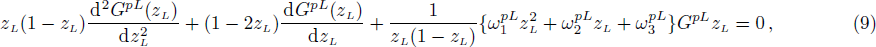
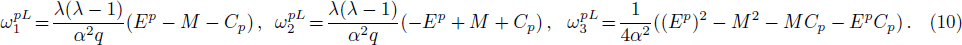
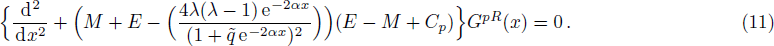
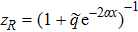
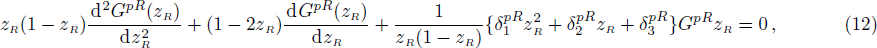
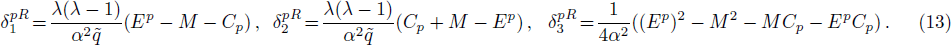
Equations (

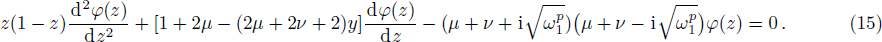

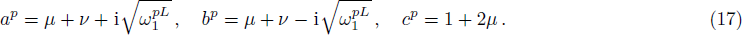
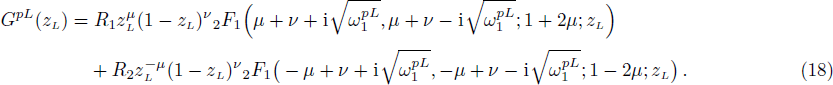
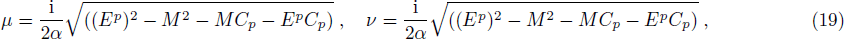

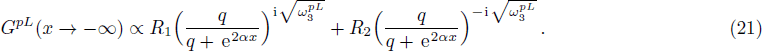
The right-side solution is written as
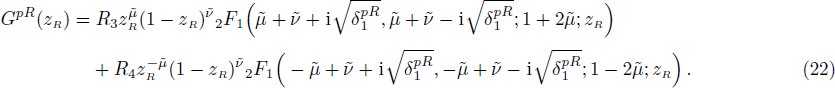
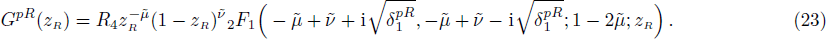
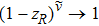
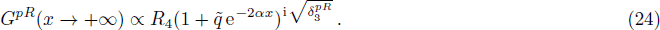
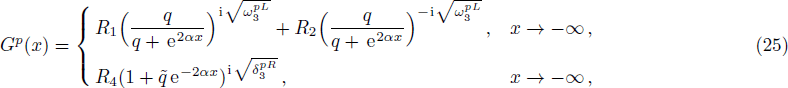

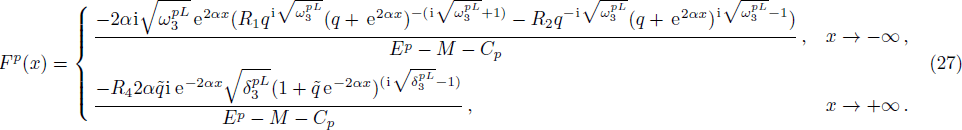
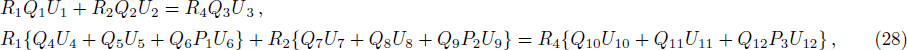
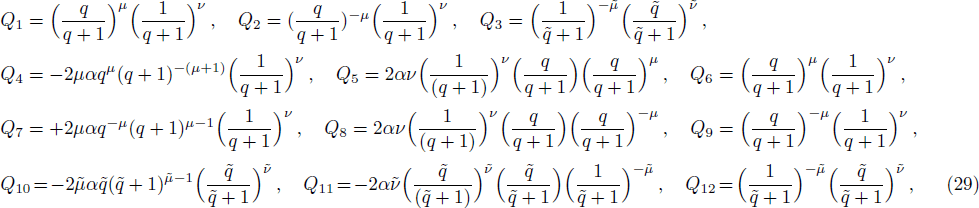
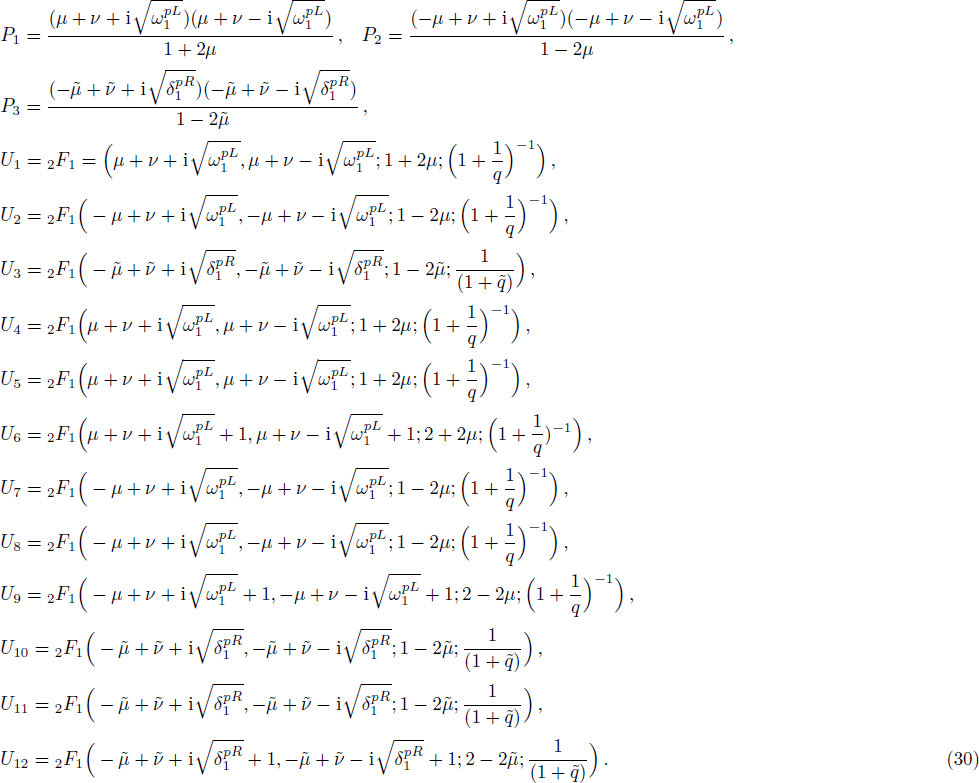
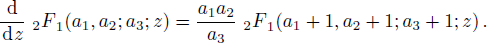
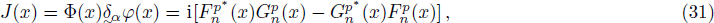


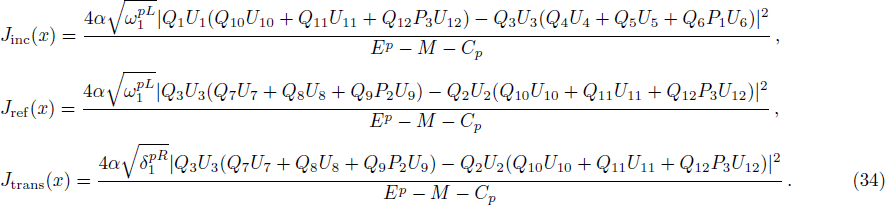
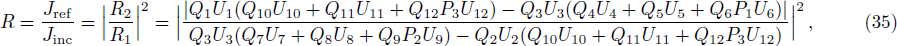
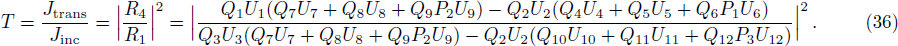
Here we solve the problem with Δ(x) = Cs = const. and so ∑(x) has the asymmetric qHPT (V(x)) in Eq. (
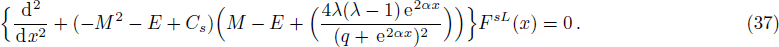
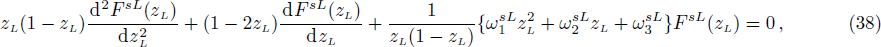
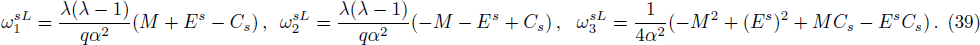
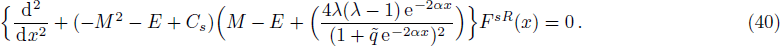
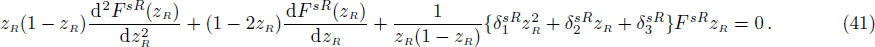
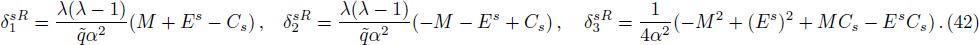
Again we sought for the scattering states for Δ(x) = constant by defining the trial wave functions as

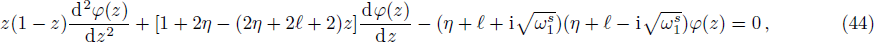


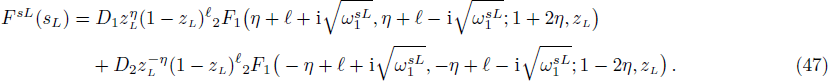


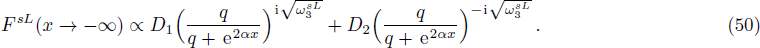
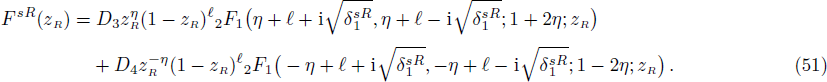
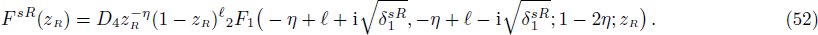
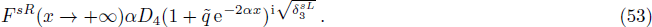
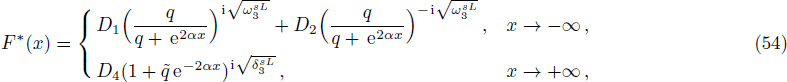

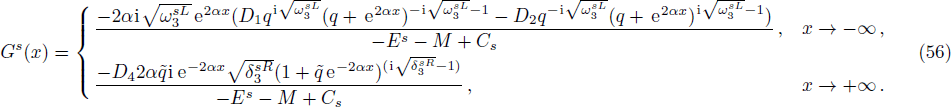

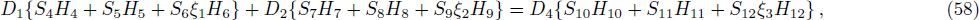
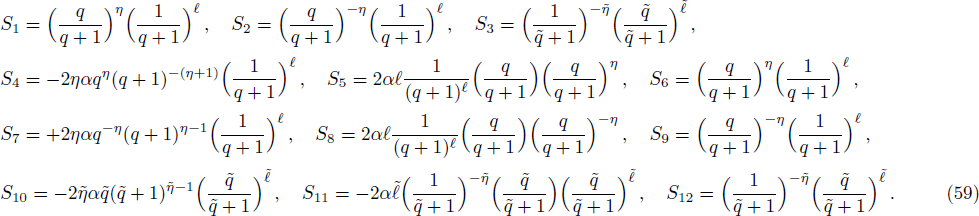
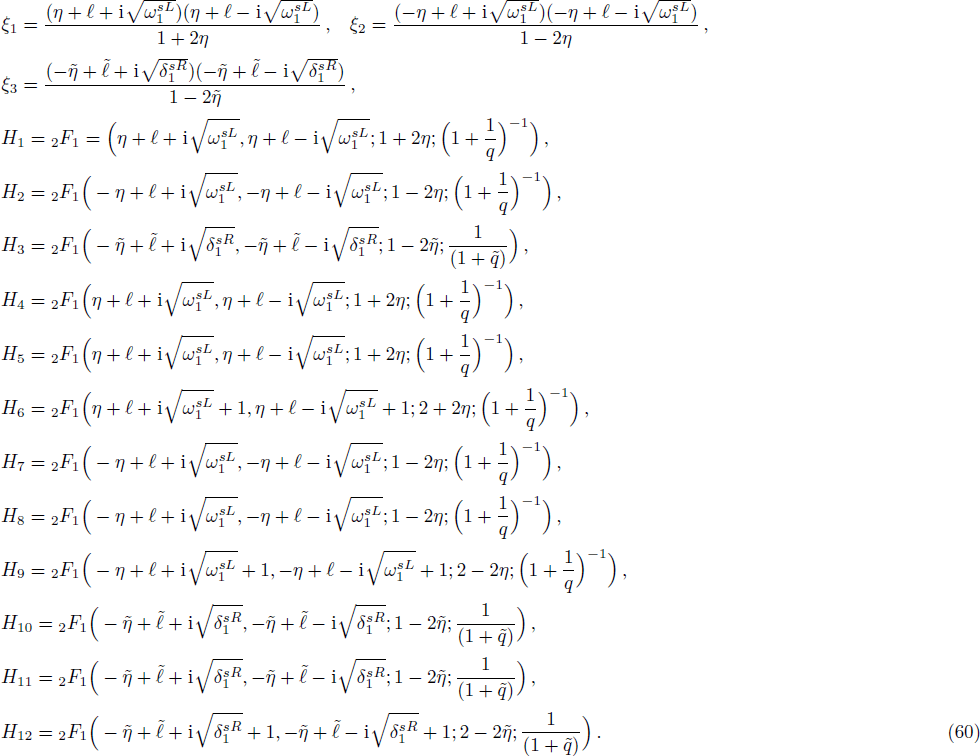
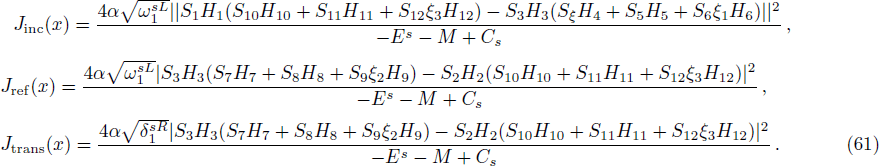
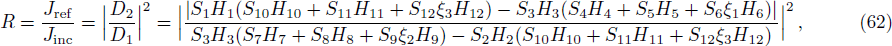
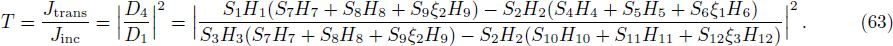
In order to find the bound state solution for the Dirac particle with qHPT, we map 4λ(λ − 1) → − V0 and the potential assume a square well form. Accordingly Eq. (
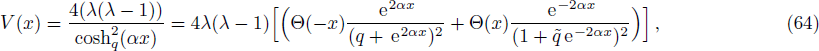
The bound state solutions can be calculated by changing the variable in this region as z = (1 + (1/q)e2αx)−1 and taking into consideration the changes in the potential so that Eq. (
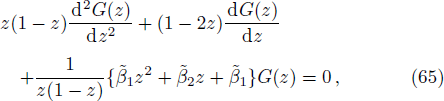
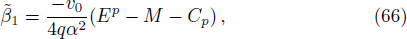
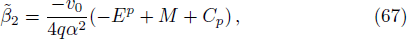
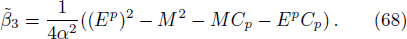
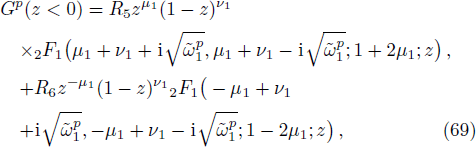
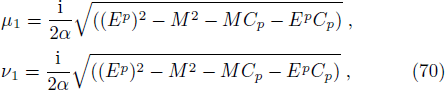
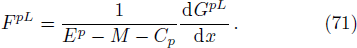
In the positive region, we define the variable 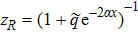
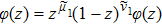
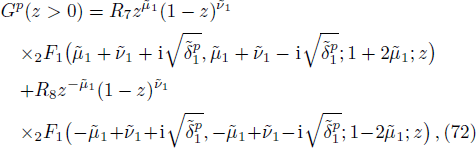
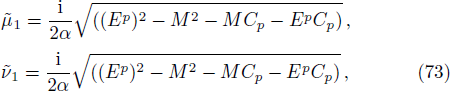
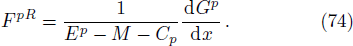

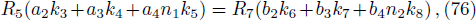
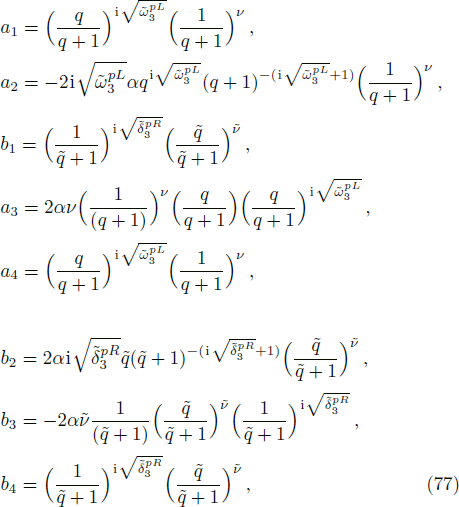
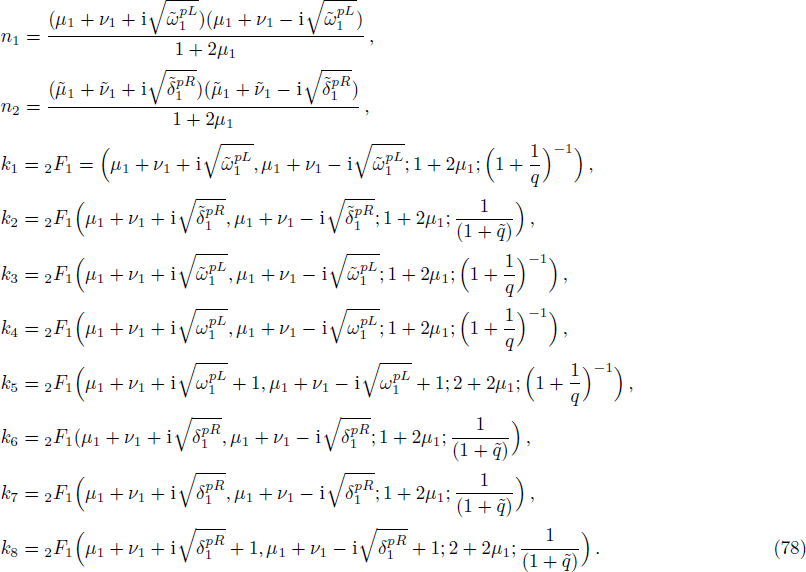

In order to solve the bound state we repeat the process shown in the formal section but here we take note of the changes made in the potential. On substituting Eq. (
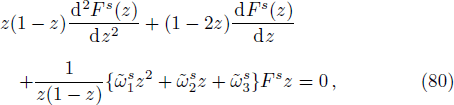
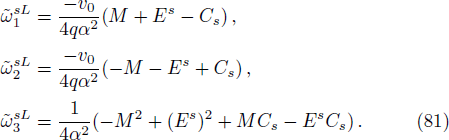
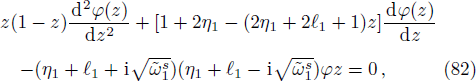
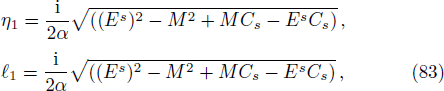
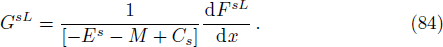
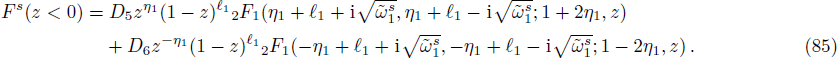
On substituting by the same steps, using also the trial wave function 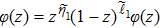
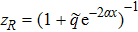
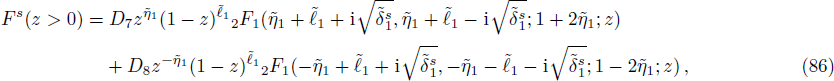
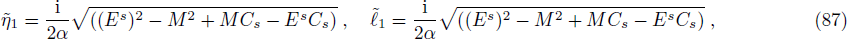



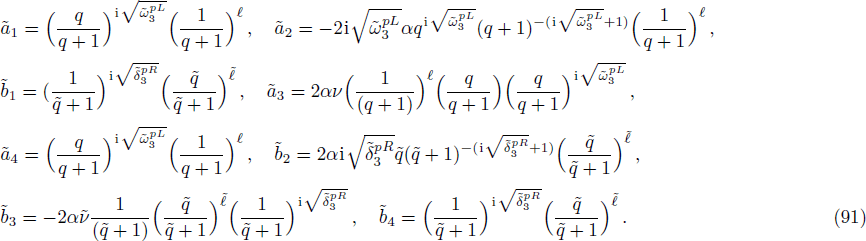
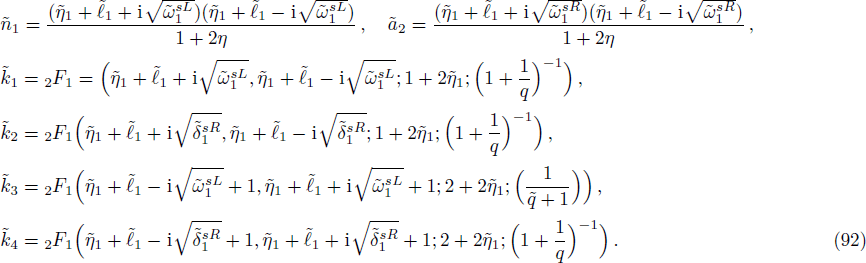

We have solved the exact solution of a relativistic one-dimensional Dirac equation for the asymmetric q-parameter hyperbolic Pöschl-Teller potential and have obtained in terms of hypergeometric functions the scattering states as well as transmission and reflection coefficient using the continuity conditions of the wave function and its derivatives. The bound state solution is obtained by vanishing the determinant of the coefficients of the wave function for the pHPT potential. This study can find its applications to physics especially condensed matter Physics in view of the recent development in grapheme QD materials.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] |

