† Corresponding author. E-mail:
Supported by the National Natural Science Foundation of China under Grant Nos. 11705077 and 11775104, Natural Science Foundation of Zhejiang Province under Grant No. LY14A010005 and Scientific Research Foundation of the First-Class Discipline of Zhejiang Province (B) (No. 201601)
With the aid of the truncated Painlevé expansion, a set of rational solutions of the (2+1)-dimensional generalized Nizhnik-Novikov-Veselov (GNNV) equation with the quadratic function which contains one lump soliton is derived. By combining this quadratic function and an exponential function, the fusion and fission phenomena occur between one lump soliton and a stripe soliton which are two kinds of typical local excitations. Furthermore, by adding a corresponding inverse exponential function to the above function, we can derive the solution with interaction between one lump soliton and a pair of stripe solitons. The dynamical behaviors of such local solutions are depicted by choosing some appropriate parameters.
The (2+1)-dimensional Korteweg-de Vries (KdV) equation introduced by Boiti et al. can be expressed[1]
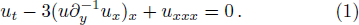
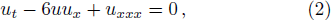
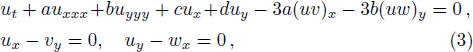
One of valid ways to describe nonlinear phenomena is to derive various kinds of explicit solutions in the appropriate physical models, such as typical solitons and traveling wave solutions in nonlinear science. Recent advances in integrable systems, computer technics and numerical approaches have brought the development of effective techniques to search for these solutions. These powerful approaches include the inverse scattering method (a method which can be used to solve the initial value problem for certain classes of nonlinear partial differential equations),[7] the bilinear method (a new stability-preserving order reduction approach),[8] the Bäcklund transform (which is typically a system of first order partial differential equations relating two functions, and often depending on an additional parameter).[9] The typical methods also include the truncated Painlevé expansion,[10] the similarity reduction,[11] the hyperbolic function method[12] and so on.
This paper is presented as follows. In Sec.
A lump soliton structure is localized in both space directions and described in a fully developed rogue wave (RW) which can be expressed by one suitable rational function.[13] For this purpose to the GNNV equation (
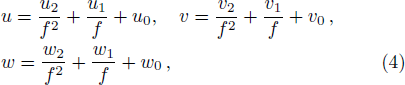
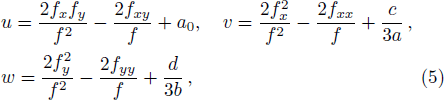
To search for the lump and its corresponding structures, we need to take the following quadratic function f, which has been proved effectively to the Kadomtsev-Petviashvili (KP)-like equations[16–23]
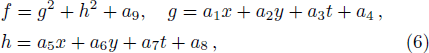
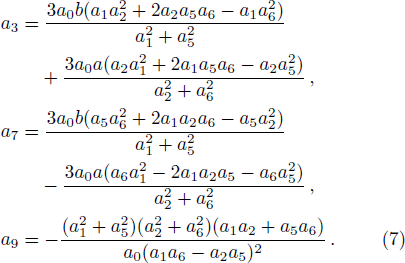
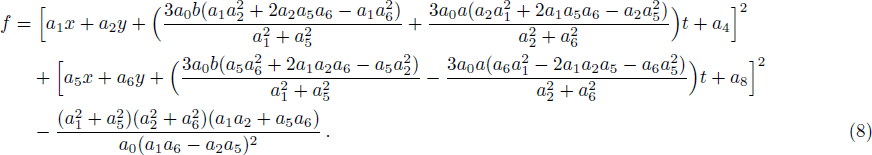
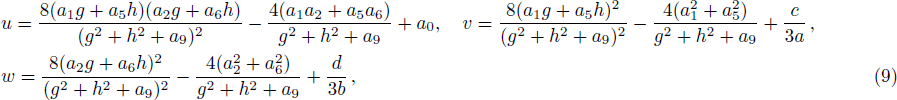
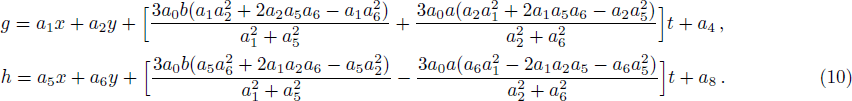
Although the parameters a1, a2, a4, a5, a6, and a8 are arbitrary, the solution should be well defined, which means two columns (a1, a2) and (a5, a6) out of proportion and unparallel in the (x, y)-plane, and the lump soliton solution could be taken shape. For this case, it can be seen from Eq. (
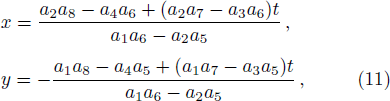
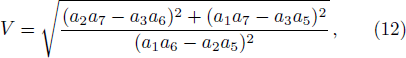
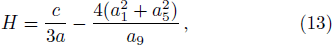
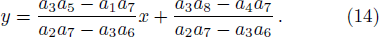
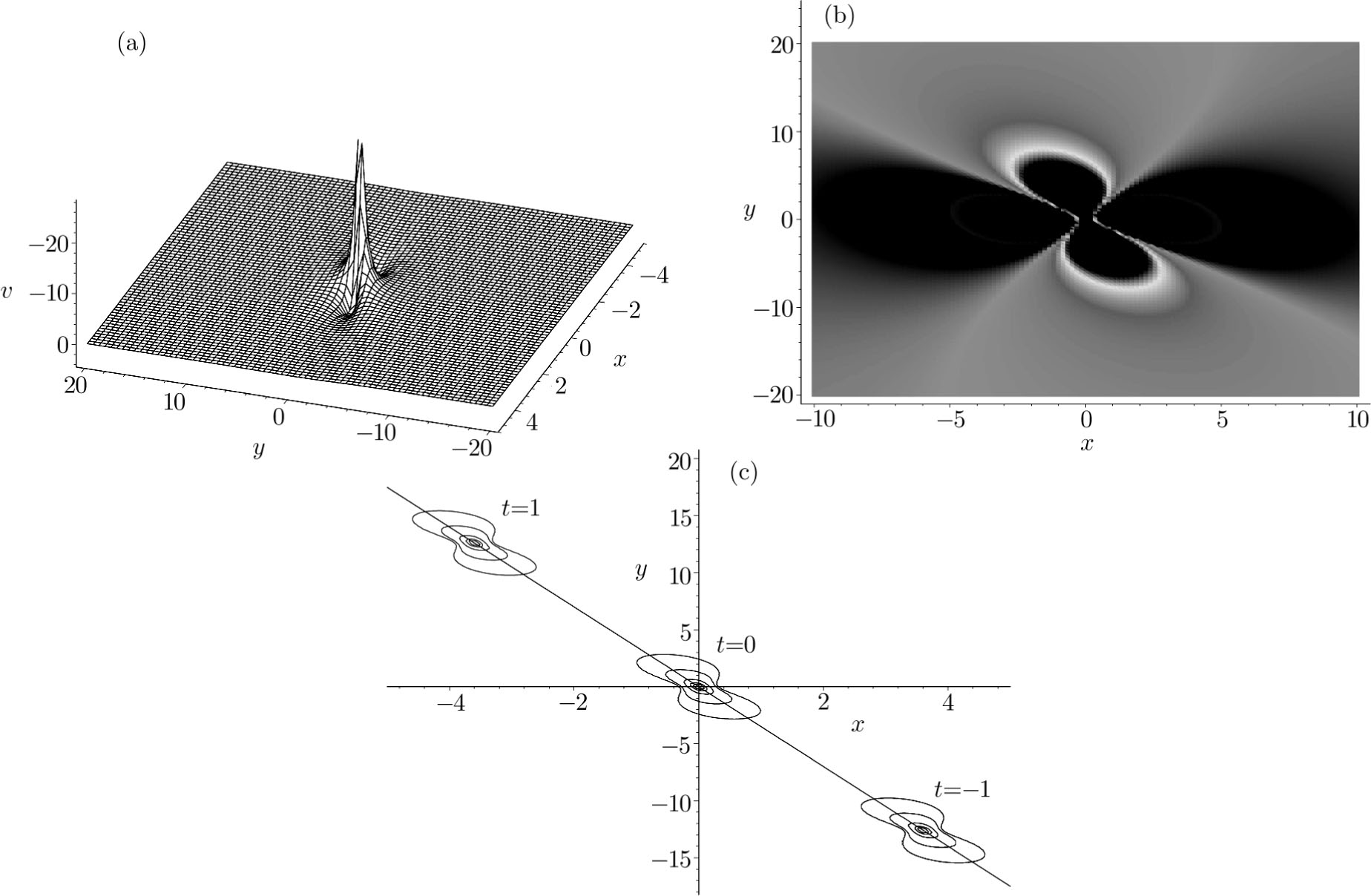 | Fig. 1. Profiles of the solution v in Eq. ( |
As a typical example, we choose the parameters a = b = c = d = a2 = a5 = 1, a0 = a1 = 2, a4 = a8 = 0, a6 = −1, so a3 = −27/5, a7 = 81/5, a9 = 5/9. The conditions a1a5 ≠ 0, a2a6 ≠ 0, a1a6 − a2a5 ≠ 0, and a0(a1a2 + a5a6) ≠ 0 are guaranteed, one lump solution is shown explicitly in Fig. 
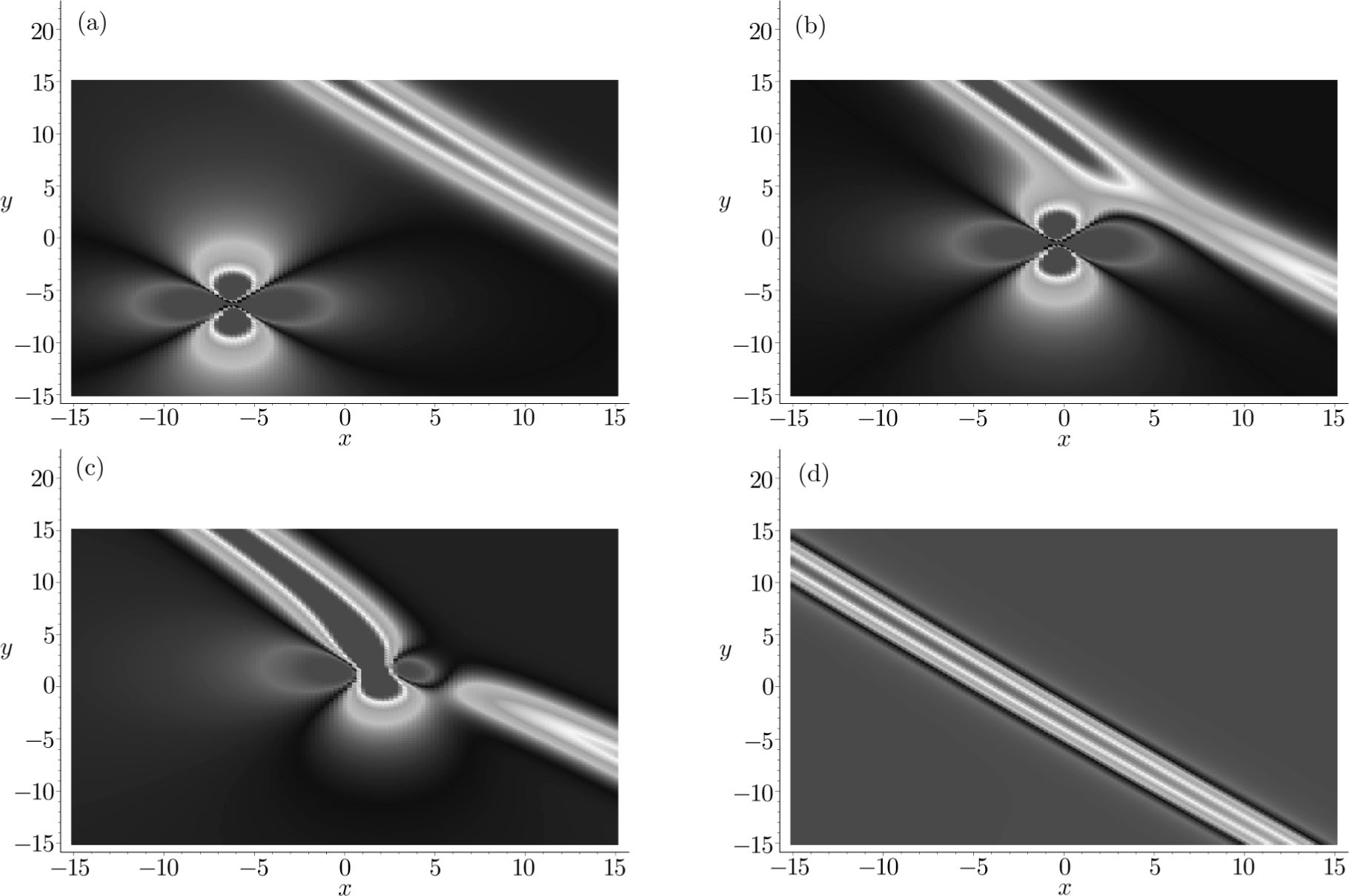
This section is to describe the interaction between one lump soliton and a stripe soliton with fusion and fission phenomena. Generally speaking, the elastic collision between solitons in an integrable model is one of the most important phenomena in soliton theory which means the velocity, amplitude and wave shape of each soliton do not change after their interaction.[24–25] However, in some special circumstances, the interactions between soliton excitations such as peakons and compactons of some integrable models are not completely elastic.[26] In particular, two or more solitons may fuse into one while one soliton may fission into two or more. Such phenomena are often called soliton fusion and fission.[27–28] Indeed, these phenomena have been found in many physical fields like plasma physics and hydrodynamics.[29–30]
In the following, we seek for the fusion and fission phenomena for the (2+1)-dimensional integrable GNNV equation (
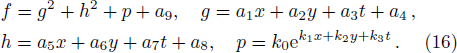
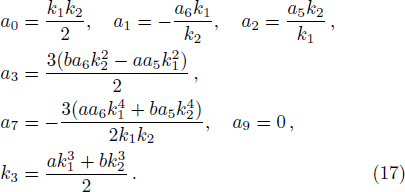
In this situation, the quadratic function solution of Eq. (
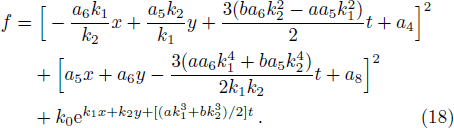
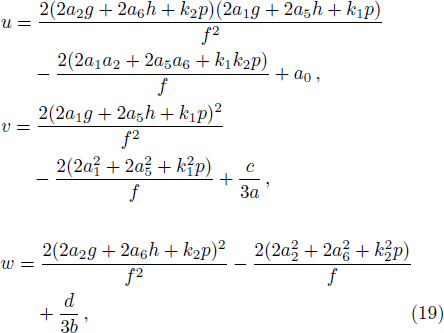
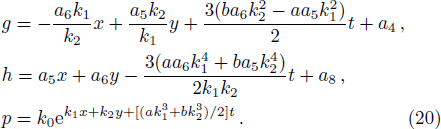
The above solution (
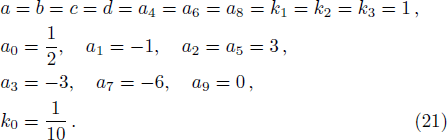
Figures
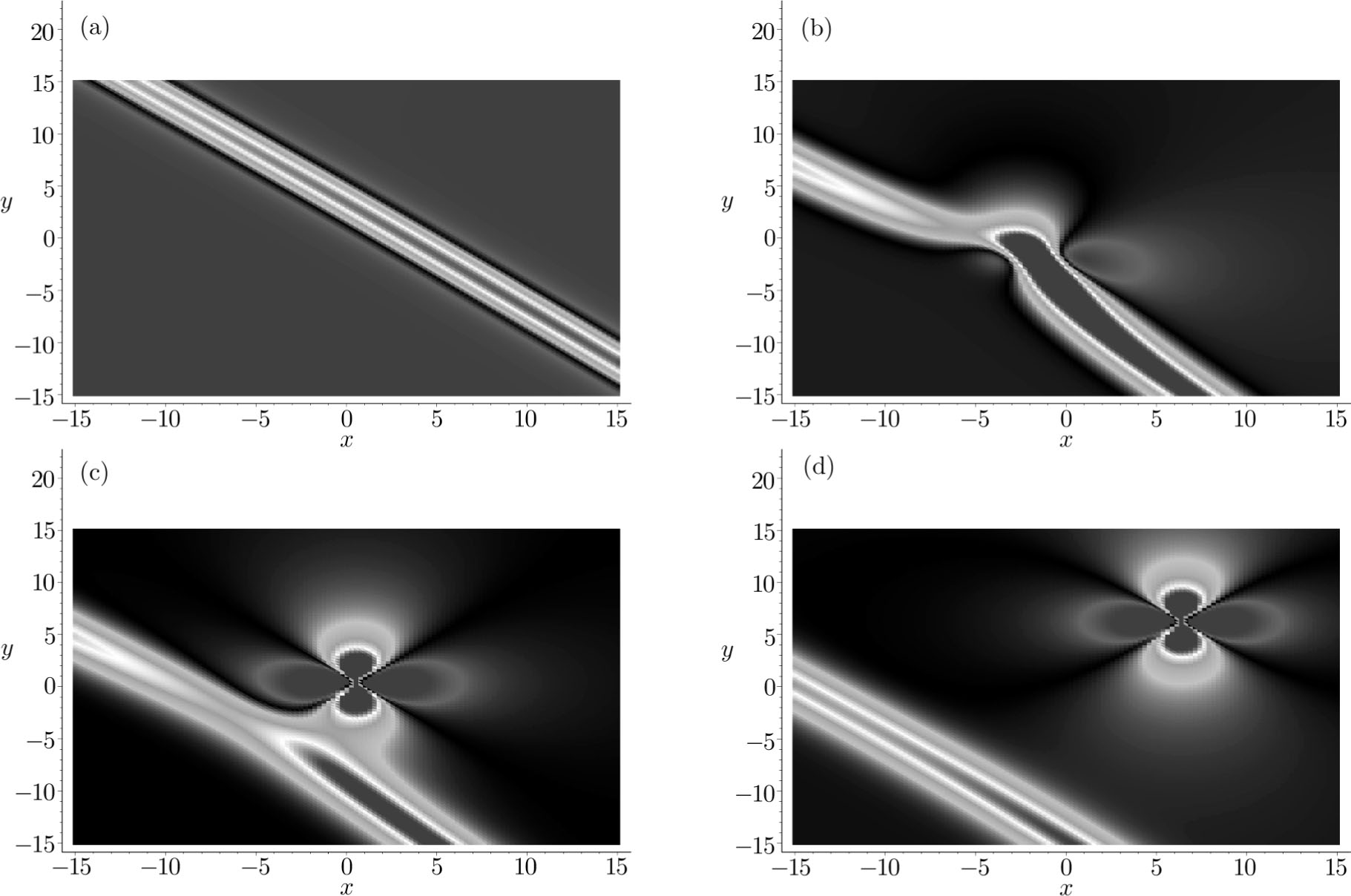
Along with the idea of the collision of one lump soliton and a stripe soliton, we start to study the collision of one lump soliton with stripe solitons pairs. To this end, we continue to add the exponential function which is a inverse one of Eq. (
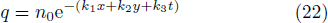
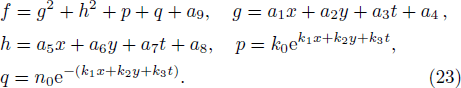
 | Fig. 4. Density figures of the interaction solution v in Eq. ( |
Substituting Eq. (
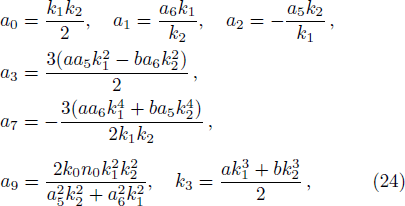
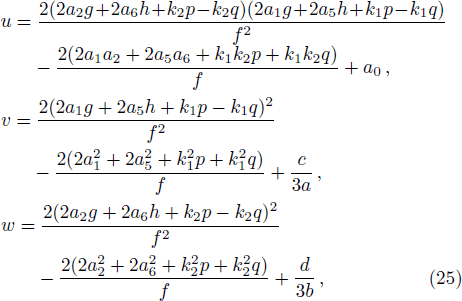
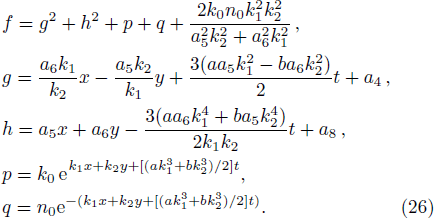
The asymptotic behavior of one lump and resonance soliton pairs can be studied according to the expression of Eq. (
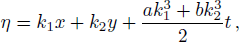
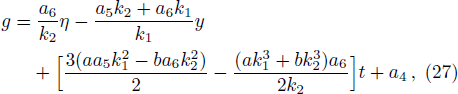
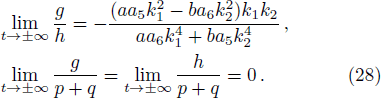
The expression (
In order to illustrate such an interaction effect, we choose the parameters as
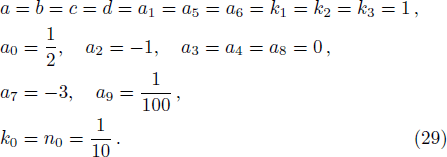
Figures
The study of the lump dynamic behaviors for the nonlinear GNNV equation firstly starts from the truncated Painlevé expansion with an auxiliary function f. By taking the auxiliary functions as the special form including the quadratic function and exponential function, we derive the lump solution, the interaction solution among one lump, a stripe soliton, and stripe soliton pairs. The lump solution is characterized by its structure localizing in all directions in the space. By combining the quadratic function with an exponential one, the interaction phenomena with fusion and fission between one lump and a stripe solitons are presented. For the interaction among one lump and a stripe soliton, there are two different physics phenomena: fusion and fission. In the process of fusion, the lump soliton and stripe soliton are independent from each other at first and as time goes on, lump soliton begins to be swallowed gradually until disappearing. The fission is an inverse progress of the fusion. As is known to all, to find the fission/fusion of the local coherent structures in a (2+1)-dimensional integrable equation is an important task. Furthermore, by introducing an inverse exponential function for the established function, one generalized solution including the stripe soliton pairs interacting with a lump is obtained. The dynamical behaviors of such local solutions are discussed mainly in density forms by choosing the appropriate parameters.
Indeed, in nonlinear science, the studying of the explicit solution about an integrable system is helpful in clarifying the underlying algebraic structure of the soliton theory and plays an important role in reasonable explaining of the corresponding natural phenomenon and application. These related localized excitations and their behaviors are originated from many natural sciences, such as fluid dynamics, plasma physics, solid physics, superconducting physics, condensed matter physics and optical problems.[31–34] In fact, it is of interest to study such types of analytical solutions. As we know, the soliton and solitary wave are two typical nonlinear structures widely appearing in many physical fields such as ocean. Here we mainly devote to obtain the interaction of lump and stripe soliton solutions from the original model equation. It is expected to the realistic physical interpretation and experiment observation. For instance, in recent work,[35] the oblique propagation of ion-acoustic soliton-cnoidal waves was reported in a magnetized electron-positron-ion plasma with superthermal electrons.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] |