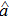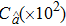Cite this Article
Kumbhakar Manotosh, Saha Jitraj, Ghoshal Koeli, Kumar Jitendra, Singh Vijay P.. Vertical Sediment Concentration Distribution in High-Concentrated Flows: An Analytical Solution Using Homotopy Analysis Method. Communications in Theoretical Physics, 2018, 70(3): 367  
Permissions
Vertical Sediment Concentration Distribution in High-Concentrated Flows: An Analytical Solution Using Homotopy Analysis Method
Kumbhakar Manotosh1, *, Saha Jitraj2, Ghoshal Koeli1, Kumar Jitendra1, Singh Vijay P.3
Department of Mathematics, Indian Institute of Technology Kharagpur, Kharagpur 721302, India
Department of Mathematics, National Institute of Technology, Tiruchirappalli, Tamil Nadu 620015, India
Department of Biological and Agricultural Engineering & Zachry Department of Civil Engineering, Texas A&M University, College Station, TX 77843, USA

 

† Corresponding author. E-mail: manotosh.kumbhakar@gmail.com

Abstract
Abstract

Transport of suspended sediment in open channel flow has an enormous impact on real life situations, viz. control and management of reservoir sedimentation, geomorphic evolution such as dunes, rivers, and coastlines etc. Transport entails advection and diffusion. Turbulent diffusion is governed by the concept of Fick’s law, which is based on the molecular diffusion theory, and the equation that represents the distribution of sediment concentration is the advection-diffusion equation. The study uses the existing governing equation which considers different phases for solid and fluid, and then couples the two phases. To deal with high-concentrated flow, sediment and turbulent diffusion coefficients are taken to be different from each other. The effect of hindered settling on sediment particles is incorporated in the governing equation, which makes the equation highly non-linear. This study derives an explicit closed-form analytical solution to the generalized one-dimensional diffusion equation representing the vertical sediment concentration distribution with an arbitrary turbulent diffusion coefficient profile. The solution is obtained by Homotopy Analysis Method, which does not rely on the small parameters present in the equation. Finally, the solution is validated by comparing it with the implicit solution and the numerical solution. A relevant set of laboratory data is selected to check the applicability of the model, and a close agreement shows the potential of the model in the context of application to high-concentrated sediment-laden open channel flow.

Keyword:open channel flow;diffusion equation;hunt equation;homotopy analysis method
1 Introduction

Transport of sediment in fluvial processes has been a long standing topic of research.[1–11] It plays a significant role in the control and management of reservoir sedimentation, geomorphic evolution such as dunes, river, and coastlines, etc. that have immense importance in our day to day life. Better understanding of sediment transport mechanism in natural watercourses needs knowledge of open channel flow. Sediment transport in open channel flow occurs mainly in two different modes, namely, bed-load and suspended load.[12] The part of the load that travels close to the bed is bed-load, while the other part travels in suspension as suspended load. In the study of suspended load, the spatial distribution of sediment concentration is of primary interest as it helps determine the discharge of suspended particles in watercourses, bed-load transport rate, and so on. The present study focuses on the vertical distribution of suspended sediment concentration in open channel turbulent flow.

The governing equation for sediment concentration distribution, termed as advection-diffusion equation (ADE), has the origin in Fick’s law of diffusion. Rouse[7] was the pioneer in this field to provide an analytical expression for vertical concentration profile by balancing the upward diffusion and the downward settling of sediment, and the solution provided by him is widely known as the Rouse equation. However, it has a major drawback that it cannot predict the sediment concentration values well near the channel bed or near the water surface, which might be due to the inclusion of Prandtl-von Kármán velocity profile that does not model velocities well in sediment-laden flows.[13] Following the work of Rouse,[7] different modifications have been done by researchers to overcome those drawbacks by incorporating several turbulent mechanisms.[6,9,11,14–15] On the other hand, Hunt[3] analyzed the dynamics of particle suspension by treating the fluid phase and the solid phase separately, and then coupled the phases by decomposing the vertical velocity of the particle into the vertical flow velocity and the particle settling velocity in a quiescent fluid. The Hunt equation has more practical importance, as unlike the Rouse equation, it can be applied to a region where the volume occupied by the particles is appreciable. For simplicity, Hunt[3] assumed the turbulent diffusion coefficient to be the same as sediment diffusion coefficient, which is a poor approximation valid only in the case of small particles as mentioned in his work. Later on, different experimental investigations revealed the non-equality of these coefficients for different flow conditions,[16–18] and different models on these coefficients are reported in literature.[9,19]

Numerous studies have been undertaken to investigate the vertical distribution of sediment concentration starting from the Hunt equation. But most of the researchers took the turbulent and sediment diffusion coefficients to be equal limiting the application of their studies. Very few researchers[6,20–21] considered the two coefficients to be different, and solved the equation numerically as the traditional analytical techniques did not succeed due to the non-linearity of the diffusion equation. To deal with the non-linear ODE-PDEs, classical perturbation[22] and asymptotic techniques[23–24] are widely applied to obtain analytic approximations of nonlinear problems in science and engineering. Unfortunately, perturbation and asymptotic techniques are too strongly dependent upon small/large physical parameters present in the governing equation, and thus are often valid only for weakly nonlinear problems.

The present study aims to derive an explicit analytical solution of the generalized diffusion equation with arbitrary turbulent diffusion coefficient, by means of a novel unified method, known as Homotopy Analysis Method (HAM). Liao[25] developed HAM to solve non-linear differential equations, which employs the concept of homotopy from topology to generate a convergent series solution for nonlinear systems. It has been proved[26] that the method is a unified one, which logically contains Lyapunov’s small artificial parameter method,[27] Adomian decomposition method,[28] Homotopy perturbation method (HPM),[29] the δ-expansion method,[30] and the Euler transform[31] as special cases. In summary, HAM distinguishes itself from various other analytical methods in three respects: (i) it does not directly rely on small physical parameters present in the governing equation; (ii) it assures the convergence of a non-linear differential equation; and (iii) it has flexibility regarding the choice of base functions and the auxiliary linear operator of the homotopy. Since its inception, HAM has successfully been applied to different fields of science and engineering.[32–44] The derived analytical solution obtained via HAM in the present study is validated with the implicit solution and with the 4th order Runge-Kutta (RK) method. The model is also compared with relevant experimental data on vertical sediment concentration of high-concentrated flow.

2 Mathematical Model

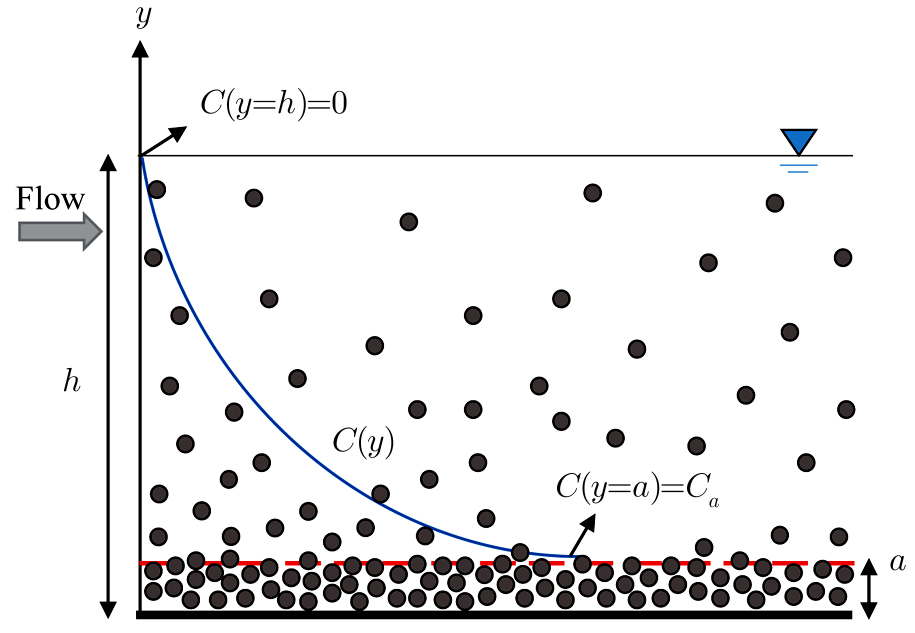
A sediment-laden flow of depth h in a wide open channel, in which the time-averaged suspended sediment concentration decreases monotonically from a maximum value Ca at the reference level y = a to zero at the water surface, is presented in Fig. 1. The formulation of the generalized diffusion equation representing sediment concentration and the methodology to obtain the analytical solution is described in what follows.

Fig. 1 Schematic diagram of sediment concentration distribution along a vertical in open channel turbulent flow over a sediment bed; within the reference level y ≤ a, sediments move as bed load, and above that as suspended load.
2.1 Governing Equation

In the case of steady-uniform flow where sediment concentration varies only in the vertical direction, the generalized governing equation can be written as:[3]

where C is the volumetric suspended sediment concentration (dimensionless), y is the vertical axis, ωs is the settling velocity of sediment particles, and εs and εt are sediment and turbulent diffusion coefficients, respectively. The ratio of εs to εs is denoted by a proportionality factor β. In general, β is assumed to be a constant over the entire depth of flow. Hunt[3] assumed β ≈ 1 (i.e., εs ≈ εs) for simplicity. However, experimental results revealed that β ≈ 1 for finer sediment particles only, and β < 1 for coarse sediment particles.[16–18] On the other hand, using the experimental results reported by Coleman,[45] van Rijn[9] suggested β to be greater than 1, which includes the influence of centrifugal acceleration enforcing the sediments to move outwards of an eddy, and results in an increase in the effective mixing length of eddies. Thus, the assumption β ≈ 1 may not be physically realistic.

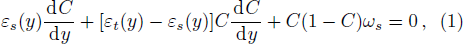
Experimental observations revealed that in the case of flow with suspended sediment particles, the flow around the neighboring settling particles exhibits a larger drag as compared to the clear water flow, known as hindered settling effect. This effect reduces the settling velocity in a sediment-laden flow from that in a clear fluid. The widely used expression for ωs was proposed by Richardson and Zaki,[46] which reads as:

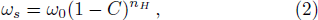
where ω0 is the settling velocity of sediment in a pure quiescent fluid, and nH is an exponent, which is termed as exponent of reduction of settling velocity. Therefore, to incorporate the real physics associated with flows carrying sediment, Eq. (2) is inserted in the governing equation (1).

The expression for εs(y) or εt(y) should be available to determine the profile of vertical concentration distribution, as can be noticed from Eq. (1). To that end, two different expressions, (namely, linear and parabolic) available in the literature, are employed in this study. They can be presented as:

where κ is the von-Kármán constant, u* is the shear velocity, and h is the maximum flow depth. The turbulent diffusion coefficient is mainly derived from the Boussenisq hypothesis based on the analogy of Newton’s law of viscosity for turbulent flow.[47] The parabolic profile was obtained by incorporating the well-known logarithmic profile for stream-wise velocity and a linear profile for Reynolds shear stress. It was shown that under steady-uniform and unidirectional open-channel flows,[9] parabolic profile estimates experimental data better than does the linear profile. It is noted that different profiles for turbulent diffusion coefficient are needed to characterize different types of flow, and thus both are considered in the present study.

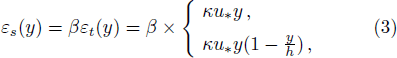
Before proceeding further, we rearrange Eq. (1) in non-dimensional form as follows:

in which

and A is the well-known Rouse number, i.e., A = ω0/βκu*. Equation (4) is a first-order highly non-linear ordinary differential equation, which represents vertical distribution of suspended sediment concentration. The solution methodology for solving Eq. (4) is described in what follows.

2.2 Implicit Solution Obtained for Eq. (4) without and with Hindered Settling Effect

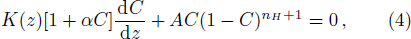
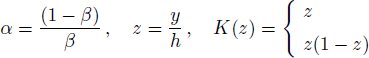
Without the effect of hindered settling, i.e., nH = 0, Eq. (4) can be rewritten as:

Using the boundary condition and integrating Eq. (5), we obtain

Further, with the effect of hindered settling through exponent nH, Eq. (4) can be rearranged as:

The volumetric sediment concentration C, which is the ratio of volume of sediment to volume of sediment-fluid mixture, takes on a maximum value 0.6 very near the channel bed.[48] Furthermore, the vertical concentration profile C monotonically decreases from the channel bed to the water surface. The present study deals with the suspended sediment concentration distribution which starts from a certain height above the channel bed, i.e., from the reference level. Thus, the reference concentration is much smaller than 0.6. Using this characteristic of C, the following approximation can be made:

Equation (8) is quite accurate due to the smallness of C in the region [a, h]. Using the approximation Eq. (8) in Eq. (7), and then integrating using the boundary condition, one can obtain the implicit solution in the following form:

Equations (6) and (9) represent implicit solutions for the vertical sediment concentration distribution without and with the effect of hindered settling, respectively. The right hand side of Eqs. (6) and (9) can easily be integrated with the substitution of linear and parabolic profiles for K(z) mentioned previously.

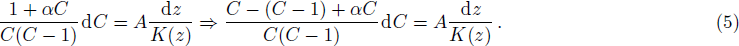
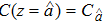
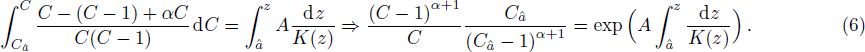
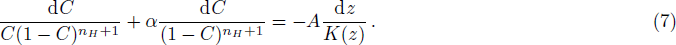
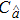
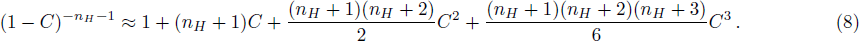
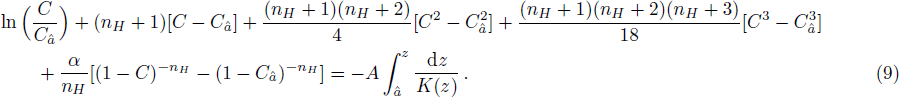
However, Eqs. (6) and (9) are only implicit solutions. Our objective is to find an explicit analytical solution to Eq. (4). Explicit functions have many advantages over the implicit ones, for example, one can describe the characteristics of the dependent variable explicitly dependent on the independent variable, and an application to that would be to find out the suspended load transport rate, which is the integration of the product of sediment concentration and velocity over the flow depth. The present study, therefore, shows the potentiality of a novel unified mathematical method, called, Homotopy Analysis Method (HAM), for handling non-linear differential equations arising in various field of science and engineering.

2.3 Solution Obtained by HAM

We suggest this unified method, HAM, not only for solving the equation modeled in this study but for any strong non-linear problem arising in the field of hydraulics, especially sediment transport phenomenon; therefore, for the sake of completeness, here we briefly present the methodology (as proposed by Liao[26]) associated with it in a convenient way. For that purpose, let us consider the original non-linear Eq. (4) in the following form:

where is a non-linear operator, C(z) is the unknown function, and z is the independent variable. One can construct the homotopy function as follows:

where q ∈ [0,1] is the embedding-parameter, ħ is a non-zero auxiliary parameter, is a linear operator, and H(z) is a non-zero auxiliary function. The underlying idea behind HAM is that a continuous mapping is described to relate the solution C(z) and the unknown function Φ(z;q), with the aid of the embedding-parameter q.[25] Thus, the initial approximation C0(z) of the solution C(z) is so chosen that Φ(z;q) varies from C0(z) to C(z), as q varies from 0 to 1. Representing this mathematically, one can write Φ(z;0) = C0(z) and Φ(z;1) = C(z). We now define:

where (∂mΦ(z;q)/∂qm)|q = 0 is called the m-th order deformation derivative}. Using Taylor’s theorem, one can expand Φ(z;q) in a power series of the embedding parameter q as follows:

Assume that , H(z), C0(z), and ℏ are so properly chosen that the series Eq. (13) converges at q = 1. Then, at q = 1, the series becomes

Equation (14) provides the relationship between the initial approximation C0(z) and the exact solution C(z). However, the higher order approximations Cm(z) for m ≥ 1 are still unknown to us. Liao[25] showed that the higher order terms can be obtained by differentiating the zeroth order deformation Eq. (11) (with ) m times with respect to q, and setting q = 0, and finally dividing by m!, as follows:

where

Liao[26] proposed some generalized rule of solution expressions, rule of coefficient ergodicity, and rule of solution existence in order to choose the initial approximation, linear operator, and the auxiliary function. The importance of the auxiliary parameter ℏ lies in the fact that it provides us a convenient way to control and adjust the convergence region of the obtained series solution.

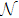
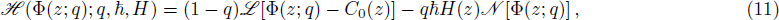
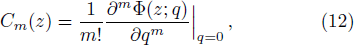
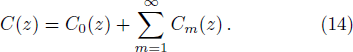
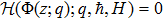
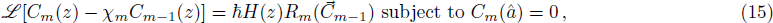
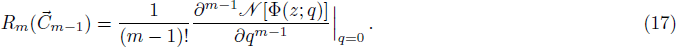
The term (1 − C)nH + 1 presents in the governing equation involves a non-integer exponent, which makes the equation highly non-linear and may take longer computational time when applying HAM. Thus, before proceeding further, we use some accurate approximation for that term similar to Eq. (8). Using the approximation, the governing Eq. (4) is rewritten as follows:

For Eq. (18), in accordance with Liao’s rule of solution expression, a single-term linear operator is chosen in order for simplicity of the subsequent derivations:

The nonlinear operator is selected as:

As pointed out by Vajravelu and Van Gorder,[49] without any loss of generality, the auxiliary function H(z) can be taken as 1. According to their analysis, the selection of H(z) is not necessary if one selects a proper or optimal linear operator . Following them, we also have taken the function to be 1 to avoid any unnecessary difficulty in the computation. The key is to find out Rm’s from Eq. (17), the first few terms are calculated as follows (“′” represents first-order derivative with respect to the independent variable z):

Proceeding like above, one can find a closed-form for Rm (m ≥ 1) corresponding to Eq. (18) as follows:

Now, applying the inverse of the linear operator Eq. (19), and using the boundary condition , one can obtain the m-th term as:

Finally, the M-th order HAM-based approximation of C(z) can be obtained explicitly as:

It can be observed from Eq. (26) that one can obtain the iteration as per wish once the initial approximation C0(z) is known. For subsequent derivations, the initial approximation is selected to achieve the HAM-based series solution.

3 Results and Discussion

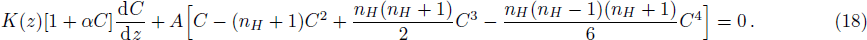
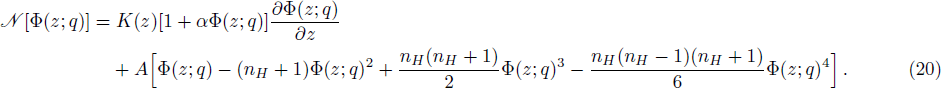
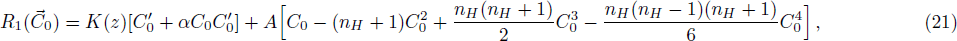
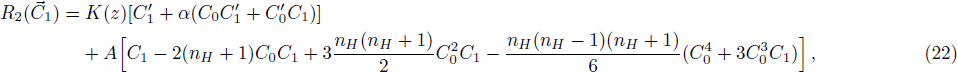
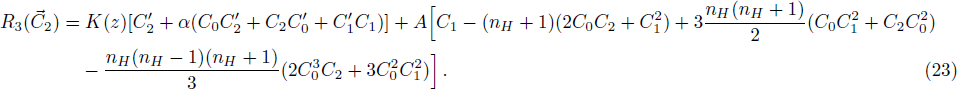
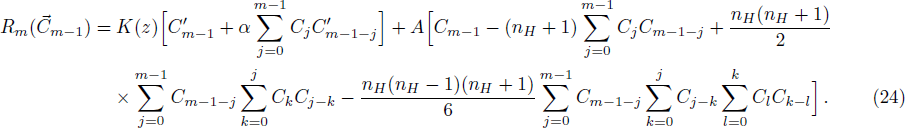
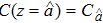
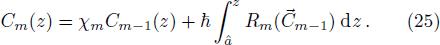
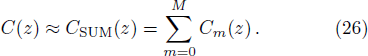
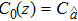
In this section, we validate the HAM-based solution given by Eq. (26) with the implicit solutions (Eqs. (6) and (9)) as well as with 4-th order Runge-Kutta (RK) method for two different profiles of K(z). Finally, the HAM-based solution is applied to a laboratory dataset of vertical concentration profile for high-concentrated flow to check the applicability of the model.

3.1 Selected Expressions for the Parameters

It is to be noted that in order to apply the derived analytical model (Eq. (26)), the Rouse number A, proportionality parameter β, and the exponent of reduction of fall velocity nH need to be computed. Many researches[46,50–51] have reported that nH depends mainly on the particle Reynolds number. Out of several formulae available, we selected the widely used expression of Richardson and Zaki.[46] According to them, nH depends on the particle Reynolds number Rep by the following relation:

in which Rep = (ω0/νf)dp, dp being the particle diameter and νf being the kinematic viscosity of clear fluid. Here, the clear water settling velocity ω0 is calculated from the well-known expression given by Cheng,[52] which reads as:

where d* is the dimensionless particle diameter, defined as, , g being the gravitational acceleration.

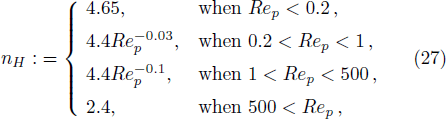
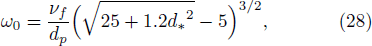
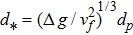
On the other hand, investigations on the determination of expression for β have been limited since the start.[9,19] Recently, Pal and Ghoshal[19] studied the nature of β by analyzing a large number of data sets of different researchers, and established two relations of β for dilute and non-dilute flows. Their study claims that β values do not only depend upon normalized settling velocity, but also on reference level and reference concentration. They developed the following expressions:

In this study, we have used the expression given by Eq. (29). The Rouse number A : = ω0/βκu* is computed using the expressions for ω0 and β given by Eqs. (28) and (29), respectively. The parameter κ is a universal constant having the value 0.41. Calculation of the reference level and the corresponding concentration is difficult in sediment transport studies because the formulae available in the literature lead to an incorrect estimation of vertical concentration values. To get rid of it, a few researchers[6,20] computed as the lowest available height reported in the observed data set and the concentration thereat as . In this study, the reference level and reference concentration are selected in the same way.

3.2 Validation of the HAM-Based Solution

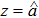
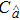
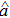
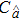
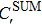
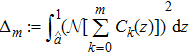
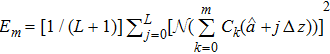
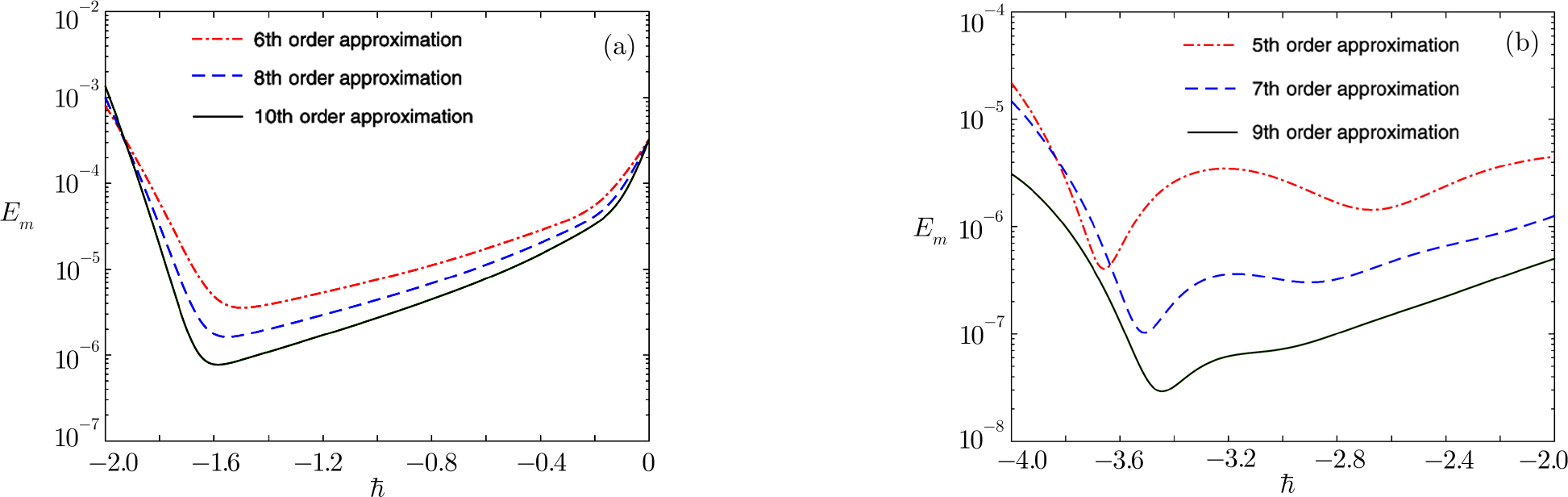It can be observed that the HAM-based series solution given by Eq. (26) is basically a function of z and ℏ. The study of Liao[26] asserts that the auxiliary parameter ℏ plays the key role in controlling the convergence of the series solution Eq. (26). Thus, a suitable choice of ℏ will lead towards the convergence of the series Eq. (26) to the exact solution for all z in its domain of definition (for detailed proof, see Appendix A). As reported in Liao,[26] the region of flatness of ℏ-curves determines the values of ℏ for which the HAM-based series CSUM converges to the exact solution C(z). Similar observation also follows for the derivative series which converges to C′(z). The mathematical justification behind this observation is given by Abbasbandy et al.,[32] However, such ℏ-curves do not produce the best value of ℏ for which the series solution rapidly converges. To that end, the exact square residual error Δm at the m-th order approximation has been introduced (Liao[53]) which is defined by . For a given order of approximation, the optimal value of ℏ is given by the minimum of Δm. But the higher the order of approximation the greater is the computational time needed to obtain the exact residual error Δm. Therefore, one can use the average residual error Em to decrease the computational time, which is given as . In Figs. 2(a) and 2(b), the average residual error Em is plotted for different orders of approximation, considering K(z) as linear and parabolic, respectively. It can be observed from the figures that for each order of approximation, there exists an optimal ℏ for which the error Em is minimum.

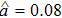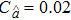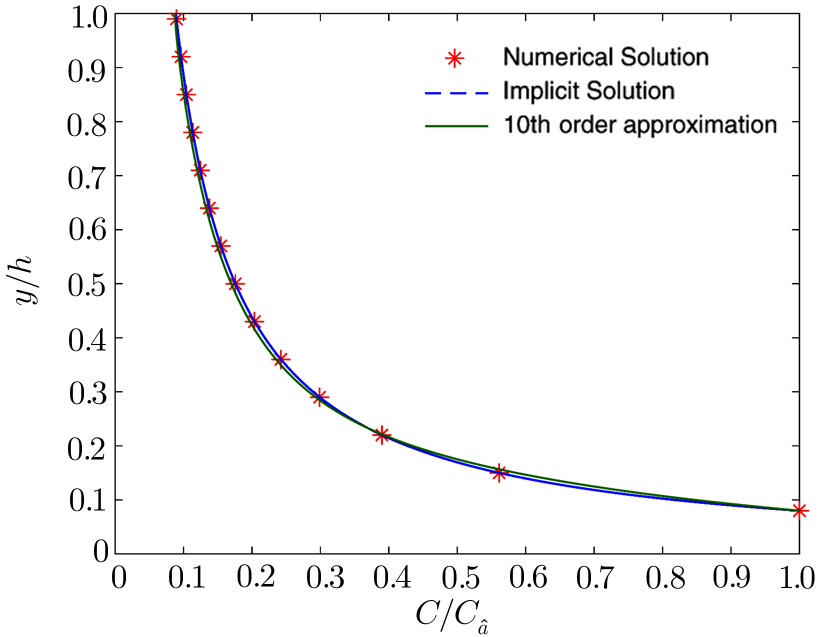
Fig. 2 Average residual error Em versus the auxiliary parameter ℏ taking A = 1, α = 0.5, nH = 4, , and . (a) K(z) as linear, (b) K(z) as parabolic.

Now, we validate the obtained HAM-based solution by comparing it with implicit solution given in Eqs. (6) and (9), and with 4th order Runge-Kutta method. For that purpose, a set of feasible values of the required parameters is chosen randomly to assess the solutions. Figsures 3 and 4 present three types of solutions: HAM-Based, implicit, and numerical solutions, for linear and parabolic K(z) profiles, respectively. The required parameter values are mentioned in the text boxes inside the figures. The auxiliary parameter ℏ is obtained by minimizing Em; the values obtained are −1.585 for the 10th order approximation with linear K(z) and −3.445 for the 9th order approximation with parabolic K(z), and HAM-based series solutions are close to both numerical and implicit solutions as seen from the figures.

Fig. 3 Validation of the HAM-based solution (for ℏ = −1.585) with numerical solution (4th order RK-method) and implicit solution considering linear profile for K(z). A = 1, α = 0.50, nH = 4, a/h = 0.08, Ca/h = 0.02, K(z) = z.
Fig. 4 Validation of the HAM-based solution (for ℏ = −3.445) with numerical solution (4th order RK-method) and implicit solution considering parabolic profile for K(z). A = 1, α = 0.50, nH = 4, a/h = 0.08, Ca/h = 0.02, K(z) = z(1 − z).
3.3 Variation of Concentration Profile with nH and A

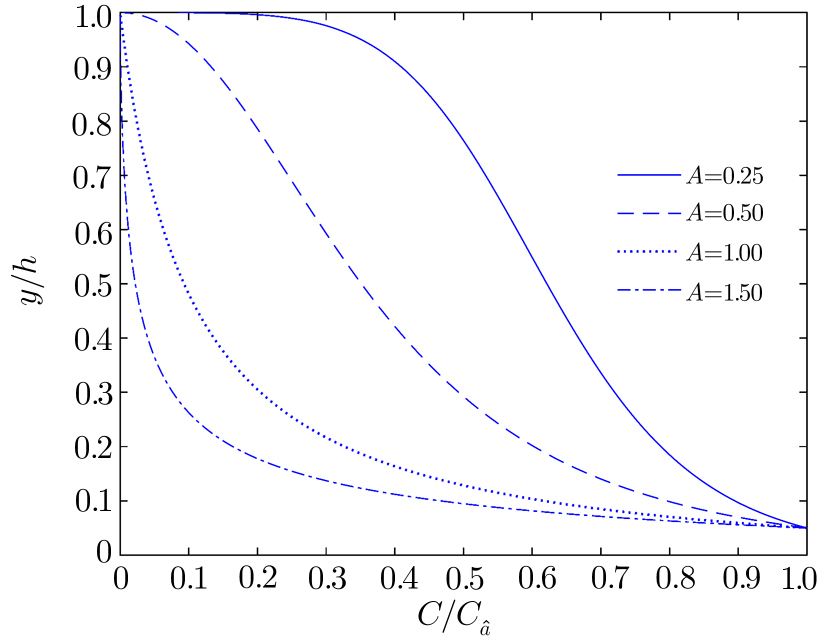
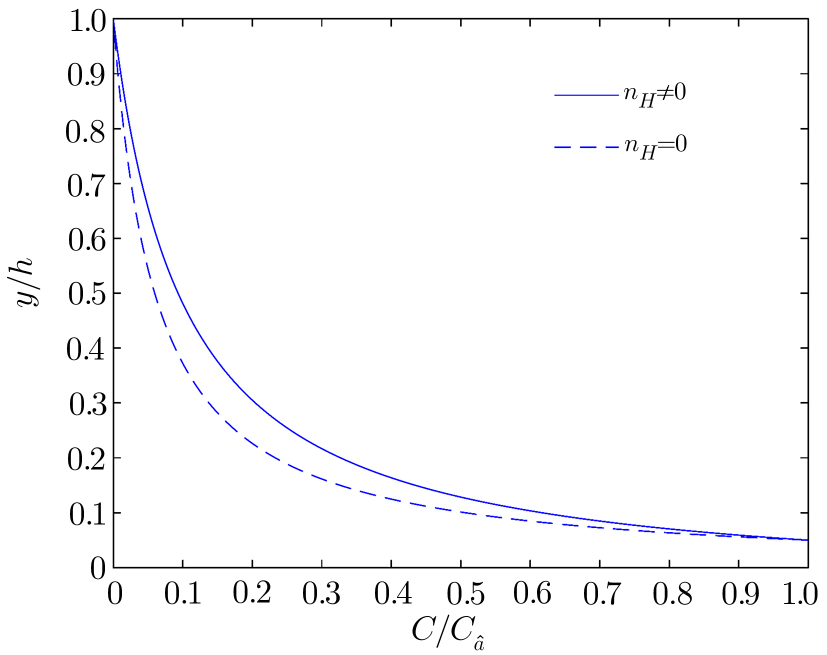The effect of hindered settling on vertical sediment concentration profile is shown in Fig. 5. It is observed from the above figure that the concentration values increase due to the effect of hindered settling. Due to the hindered settling mechanism, the downward settling of a particle is prevented by the particles present in the surrounding.

Fig. 5 Influence of hindered settling through nH on the vertical concentration profile. A = 1, α = 0.25, a/h = 0.05, Ca/h = 0.10.

Figure 5 presents two sediment concentration profiles with and without the effect of hindered settling. It is seen from the figure that the difference in concentration values is quite prominent. We observe that up to a very small distance from the channel bed and near the water surface, this difference is small. However, in the main flow region where suspension occurs, this difference is visible and decreases with the increasing vertical distance. The explanation behind these behaviors of concentration profiles is conveyed as follows. The hindered settling mechanism is not very active at the channel bed or near water surface, since the particles are not in suspension or are not mostly present there, respectively; however, in the main flow region, a large number of particles come into suspension mode due to excess bed shear stress, and the concentration difference increases thereat. On the other hand, the entrainment of sediment decreases with increasing vertical height which reduces the impact of nH and as a result, the difference of concentration values almost vanishes.

In Fig. 6, the vertical normalized concentration profiles are plotted for different values of the Rouse number A (=0.25,0.5,1, and 1.5). A smaller value of A indicates finer sediment particles, and thus for a given vertical height the concentration value decreases with an increase in A as can be seen from the figure. For coarser sediment particles, the concentration value at the free surface is vanishingly small; however, a finite value at the free surface is meaningful for finer sediment particles as observed from the figures. Moreover, interestingly, near the channel bed (for z < 0.2), the concentration curves are converging in nature for different Rouse numbers.

Fig. 6 Vertical concentration profiles for different values of the Rouse number A. a/h = 0.05, Ca/h = 0.10, nH = 4, α = 0.25.
3.4 Further Modification to the Solution and Application to Laboratory Data

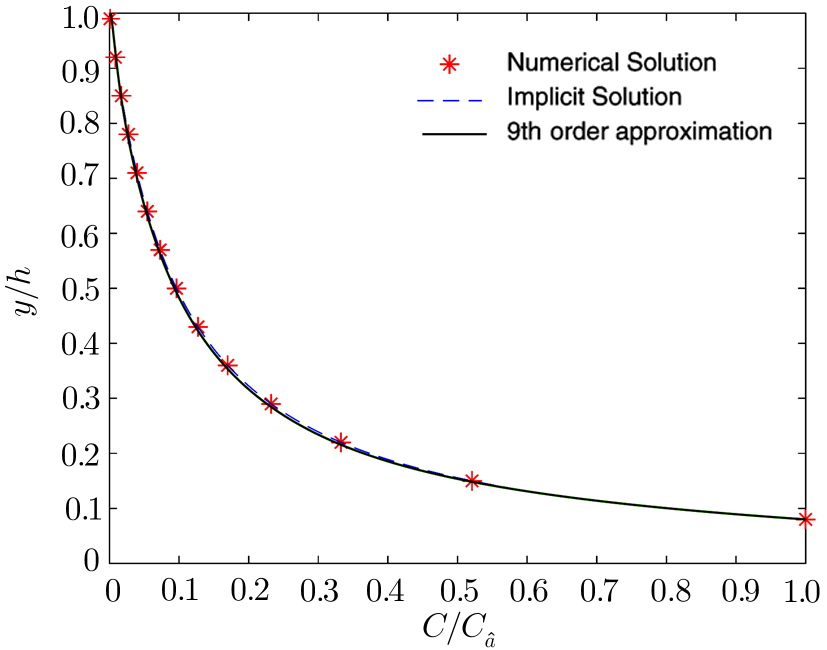
According to Liao’s rule of solution expression, one can choose the initial approximation, auxiliary linear operator, and auxiliary function with great freedom. In the previous section, we obtained the HAM-based series solution by choosing these functions. However, the solution obtained was seen to be close to the numerical solution for terms considering up to 9th order or so. Here, we further refined our choices of these functions, in accordance with the rule of solution expression of HAM, to search for a reliable 3rd–4th order analytical solution to the problem. To that end, {((1 − z)/z)n; n ≥ 0} was chosen as the set of base functions to represent the solution C(z) for the problem. 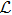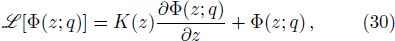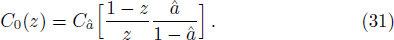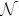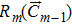Accordingly, the auxiliary linear operator and the initial approximation C0(z) were selected as follows:

The auxiliary function H(z) was chosen as 1 for simplicity, and the non-linear operator was chosen the same as that of Eq. (20). Therefore, the final solution was obtained, considering parabolic profile for K(z), as follows:

where is given by Eq. (24).

The present study considered the most generalized governing equation by taking into account the physics of sediment-laden flow through the incorporation of hindered settling effect, arbitrary K(z) profile, and the non-identity of the ratio of sediment diffusion coefficient to turbulent diffusion coefficient. Specifically, the equation modeled here is applicable for high-concentrated flows. To check the applicability of the model, a relevant set of laboratory data was chosen for verification. Experimental data of Einstein and Chien[54] was selected for verification as it is the most cited data for high-concentrated flows. They carried out their experiments in a recirculating flume of 12.2 m length and 30.7 cm width for three different particle sizes, namely, 0.274 mm, 940 mm, and 1.3 mm. The sediment concentration distribution near the channel bed is always a difficult task to measure, as it is under the influence of both sediment concentration and the channel bed, and hence, is of great importance. Einstein and Chien[54] measured concentration values very close to the channel bed, and reported 16 different measurement runs, named Run S1 to S16. We selected three test cases having three different particle diameters: S1 (1.3 mm), S6 (0.940 mm), and S12 (0.274 mm) for validation.

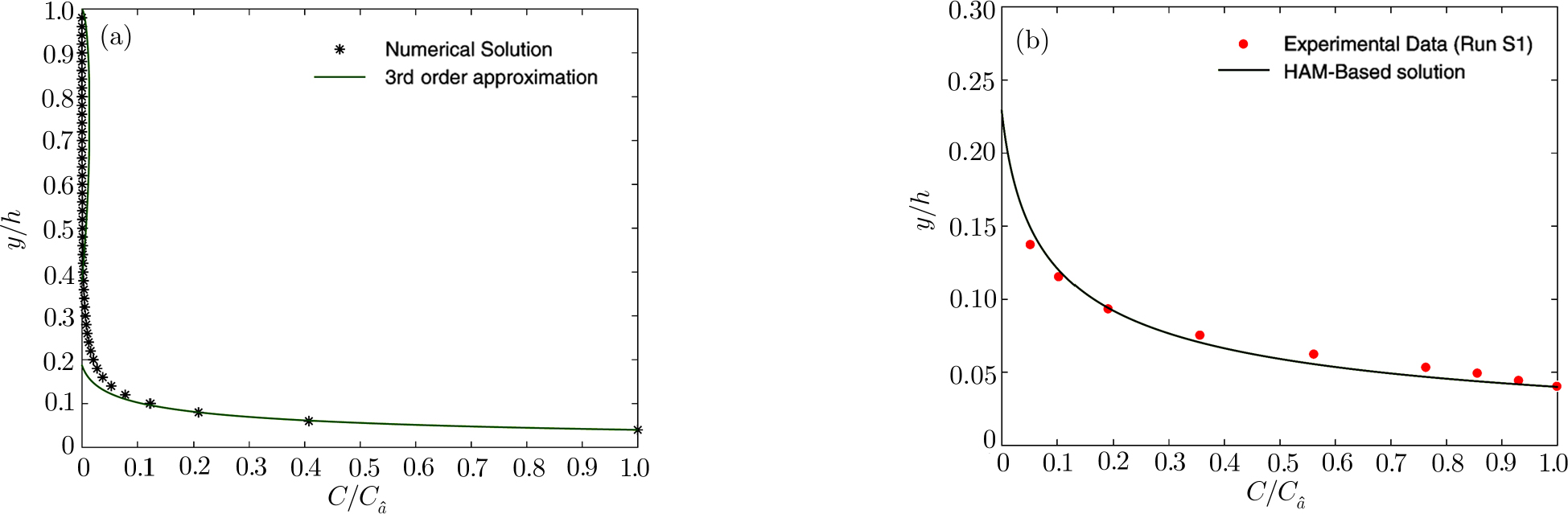Figures 7(a) and 7(b) show the validation of HAM-based solution (Eq. (26) together with Eq. (32)) with the numerical solution (the 4th order RK method) and with the experimental data set S1 from Einstein and Chien,[54] respectively. The required parameter values were computed from the formulae mentioned in the previous section and are reported in Table 1.

Fig. 7 Validation of the HAM-Based Solution (Eq. (26) with Eq. (31)): (a) with numerical solution (4th order RK method) (A = 2.212, α = −0.230, a/h = 0.04, Ca/h = 0.022, nH = 2.624, h = −0.575) and (b) with Run S1 of Einstein and Chien[54] data.
Table 1

Summary of the selected experimental data from Einstein and Chien[17] for high-concentrated sediment-laden flow.

.

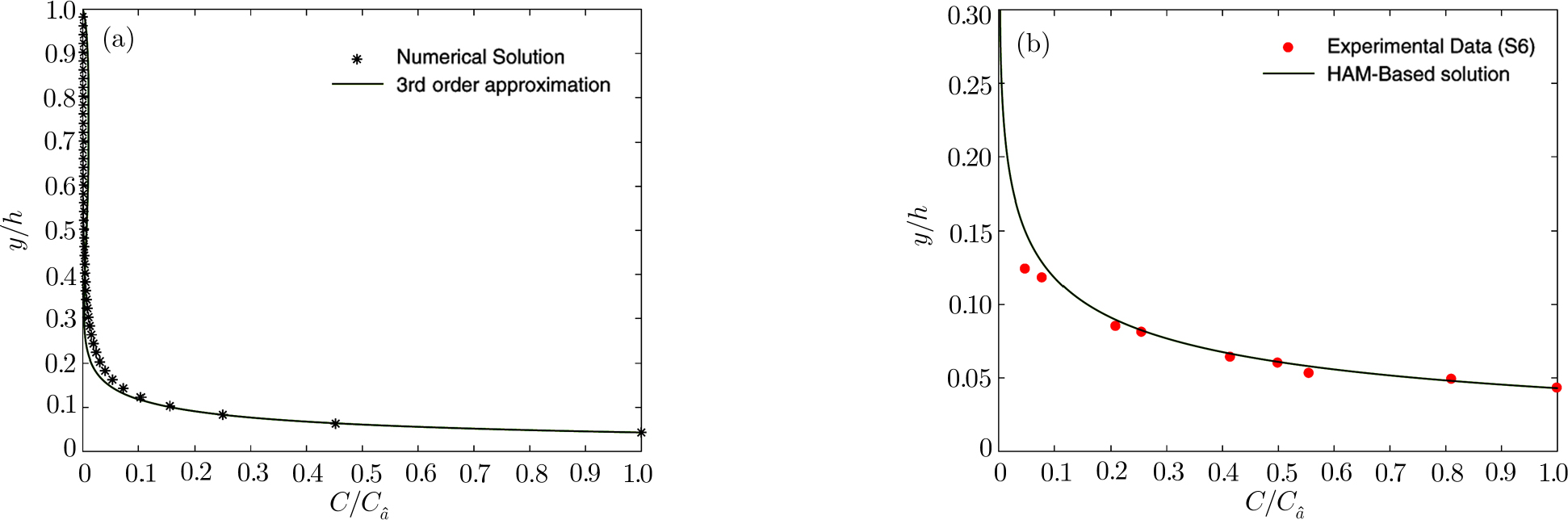It is observed that only the 3rd order approximate solution obtained by HAM given in Eq. (26) was close to the numerical one. Moreover, the corresponding solution can predict data well near the channel bed for high-concentrated sediment-laden flows as can be seen from the figure. In a similar manner, other two sets of data, namely, S6 and S12 are validated in Figs. 8 and 9. In all cases, good agreement shows potential of the present model in the context of application to particle-fluid mixture flows where the volume of particles is appreciable.

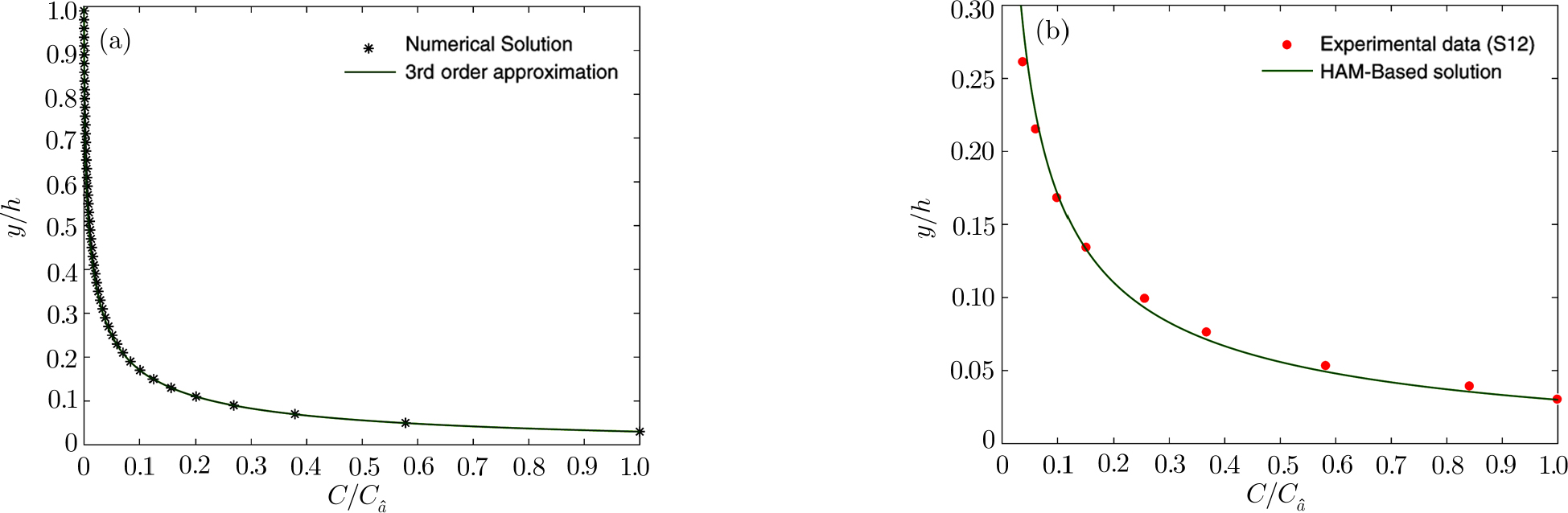Fig. 8 Validation of the HAM-Based Solution (Eq. (26) with Eq. (32)): (a) with numerical solution (the 4th order RK method) (A = 0.202, α = −0.078, a/h = −0.043, Ca/h = 0.0106, nH = 2.562, h = −0.618) and (b) with Run S6 of Einstein and Chien[54] data.
Fig. 9 Validation of the HAM-Based Solution (Eq. (26) with Eq. (32)): (a) with numerical solution (the 4th order RK method) (A = 1.444, α = 0.978, a/h = 0.03, Ca/h = 0.077, nH = 3.562, h = −0.662) and (b) with Run S12 of Einstein and Chien[54] data.
4 Conclusions

The following conclusions can be drawn from this study:

The study derives an explicit analytical solution to the most generalized governing equation for suspended sediment transport in open channels using a powerful mathematical tool, known as Homotopy Analysis Method (HAM). The method derives the solution for an arbitrary turbulent diffusion coefficient profile. Unlike the classical perturbation techniques, HAM does not rely on the presence of small/large parameters in the governing equation. Besides, the method is a generalized one, which contains several other analytical methods such as ADM, HPM, classical perturbation method etc. as special cases, and it paves the way for monitoring the convergence of the series solution through an auxiliary parameter. In all, the method can be applied to the field of hydraulics where non-linear differential equations often arise.

The governing equation for vertical sediment concentration distribution is formulated considering the different phases of fluid and solid, and then coupling both of the phases: a concept which was originally developed by Hunt, and the corresponding equation is widely known as the Hunt equation. To deal with high-concentration flow which is of great importance, sediment and turbulent diffusion coefficients are assumed to be different from each other. The effect of hindered settling on sediment particles is included in the model, and the concentration profile is analyzed due to this effect, which explains the real physics associated with high-concentrated flows.

To assess the derived analytical solution, required parameters are computed from the recent studies of the corresponding parameters. An implicit solution to the governing equation is also obtained for validating the HAM-based solution. Furthermore, the implicit solution, HAM-based solution, and the numerical solution (the 4th order RK method) are compared for different test cases considering two different profiles for eddy viscosity, namely, linear and parabolic profile.

At the end, the HAM-based solution is further achieved for different choices of the linear operator and the initial approximation to the solution. The derived solution is then seen to be close to the numerical one only for three terms of the series. Finally, to check the applicability of the derived model, a widely cited laboratory dataset on vertical concentration profile in high-concentrated flow is selected. A close agreement is found between the observed and computed values, which shows the potential of the model in the context of application to the high-concentrated free surface sediment-laden flows.

Reference
[1] Ali S. Z. Dey S. Proc. R. Soc. A 472 2016 20160749
[2] Charru F. Bouteloup J. Bonometti T. Lacaze L. Meccanica 51 2016 3055
[3] Hunt J. N. Proc. R. Soc. A 224 1954 322
[4] Kumbhakar M. Ghoshal K. Singh V. P. J. Hydraul. Div. 22 2017 04017027
[5] Kundu S. Ghoshal K. Environ. Fluid Mech. 14 2014 1357
[6] Mazumder B. S. Ghoshal K. Appl. Math. Model. 30 2006 164
[7] Rouse H. Trans. ASCE 102 1937 463
[8] van Rijn L. C. J. Hydraul. Eng. 110 1984 1431
[9] van Rijn L. C. J. Hydraul. Eng. 110 1984 1613
[10] Wang Z. B. J. Hydraul. Res. 30 1992 403
[11] Zagustin K. J. Hydraul. Res. 6 1968 163
[12] Julien P. Y. Erosion and sedimentation Cambridge University Press New York 2010
[13] Camenen B. Larson M. Report No. ERDC/CHL-CR-07-1 CEMAGREF Lyon France 2007
[14] Cantero-Chinchilla F. N. Castro-Orgaz O. Dey S. Sedimentology 63 2016 1620
[15] Umeyama M. J. Hydraul. Eng. 125 1999 653
[16] Brush L. M. Ho H. W. Singamsetti S. R. International Association for the Science of Hydraulics, IASH Commission of Land Erosion 59 1962 293
[17] Jobson J. E. Sayre W. W. J. Hydraul. Div. 96 1970 703
[18] Majumdar H. Carstens M. R. Report No. WRC-0967, Water Resources Center Georgia Inst. Technol. 1967
[19] Pal D. Ghoshal K. Environ. Earth Sci. 75 2016 1245
[20] Mazumder B. S. Ghoshal K. Int. J. Sediment Res. 17 2002 220
[21] Pal D. Ghoshal K. Appl. Math. Model. 49 2017 630
[22] Nayfeh A. H. Introduction to Perturbation Techniques Wiley Hoboken 2011
[23] Grasman J. Asymptotic Methods for Relaxation Oscillations and Applications Springer-Verlag New York 1987
[24] Lagerstrom P. A. Matched Asymptotic Expansions: Ideas and Techniques Springer-Verlag New York 1988
[25] Liao S. J. Ph.D. thesis Shanghai Jiao Tong University 1992
[26] Liao S. Beyond Perturbation: Introduction to the Homotopy Analysis Method Chapman and Hall/CRC Press Boca Raton 2003
[27] Lyapunov A. M. General Problem on Stability of Motion (English translation) Taylor & Francis London 1992
[28] Adomian G. Solving Frontier Problems of Physics: the Decomposition Method Springer Netherlands Netherlands 2013
[29] He J. H. Appl. Math. Comput. 135 2003 73
[30] Karmishin A. V. Zhukov A. I. Kolosov V. G. Methods of Dynamics Calculation and Testing for Thin-Walled Structures Mashinostroyenie Moscow 1990
[31] Agnew R. P. Amer. J. Math. 66 1944 313
[32] Abbasbandy S. Shivanian E. Vajravelu K. Commun. Nonlinear Sci. Numer. Simul. 16 2011 4268
[33] Belardinelli P. Lenci S. Demeio L. Meccanica 49 2014 1821
[34] Cheng J. Liao S. Mohapatra R.N. Vajravelu K. J. Math. Anal. Appl. 343 2008 233
[35] El-Aziz M. A. Nabil T. Meccanica 50 2015 1467
[36] Liao S. J. Int. J. Non Linear Mech. 30 1995 371
[37] Liao S. J. Chwang A. T. J. Appl. Mech. 65 1998 914
[38] Liao S. Campo A. J. Fluid Mech. 453 2002 411
[39] Ramzan M. Bilal M. Kanwal S. Chung J. D. Commun. Theor. Phys. 67 2017 723
[40] Sui J. Zhao P. Cheng Z. et al. Phys. Fluids 29 2017 023105
[41] Turkyilmazoglu M. Int. J. Mech. Sci. 102 2010 1735
[42] Vajravelu K. Sarojamma G. Sreelakshmi K. Kalyani C. Int. J. Mech. Sci. 130 2017 119
[43] Gorder Van R. A. Vajravelu K. Phys. Lett. A 372 2008 6060
[44] van Gorder R. A. Vajravelu K. Commun. Nonlinear Sci. Numer. Simul. 14 2009 4078
[45] Coleman N. L. Water Resour. Res. 6 1970 801
[46] Richardson J. Zaki W. Trans. Inst. Chem. Eng. 32 1954 35
[47] Dey S. Fluvial Hydrodynamics: Hydrodynamic and Sediment Transport Phenomena Springer-Verlag Berlin 2014
[48] Cheng N. S. Chiew Y. M. J. Hydraul. Eng. 125 1999 855
[49] Vajravelu K. Van Gorder R. Nonlinear Flow Phenomena and Homotopy Analysis: Fluid Flow and Heat Transfer Springer & Higher Education Press Heidelberg 2013
[50] Chien N. Wan Z. Mechanics of Sediment Transport ASCE New York 1999
[51] Garside J. Al-Dibouni M. R. Ind. Eng. Chem. Process Des. Dev. 16 1977 206
[52] Cheng N. S. J. Hydraul. Eng. 123 1997 149
[53] Liao S. Commun. Nonlinear Sci. Numer. Simul. 15 2010 2003
[54] Einstein H. A. Chien N. Missouri River Division Corps of Engineers US Army 1955
[55] Liao S. Homotopy Analysis Method in Nonlinear Differential Equations Springer Heidelberg 2012