† Corresponding author. E-mail:
Supported in part by Laboratory of Photonics and Quantum Measurements (LPQM) at EPFL and European Graphene Flagship under Grant No. 696656, as well as Research Deputy of Sharif University of Technology
We present a detailed calculation of the linear and nonlinear optical response of four types of monolayer two-dimensional (2D) transition-metal dichalcogenides (TMDCs), having the formula MX2 with M = Mo, W and X = S, Se. The calculations are based on 6-band tight-binding model of TMDCs, and then performing a semi-classical perturbation analysis of response functions. We numerically calculate the linear 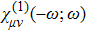
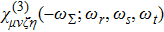
Following the discovery of the celebrated material, graphene in 2004, the field of two-dimensional (2D) materials has been rapidly expanding over the recent years.[1–9] Despite being only a monolayer thick, 2D materials exhibit extraordinary electronic, mechanical, thermal, spintronic, and in particular, optical properties. These offer novel and unprecedented applications, which were not foreseen earlier such as new nonlinear capacitors[10] for using in cryogenic parametric amplifiers, circulators, and mixers, as well as a new type of capacitive qubit referred to as cubit[11] in quantum nonlinear superconducting circuits. Of primary importance, is the nonlinear optics of the 2D materials and structures made out of them, which is a matter of current deep investigations.
A number of researches discuss the second-order nonlinear susceptibility as well as second-harmonic generation in various 2D materials.[12–16] Similarly, the third-order nonlinear optical properties of graphene has been studied in many works[17–25] and the two-dimensional nonlinear sheet susceptibility χ(3)2D or the conductivity σ(3)2D tensor of graphene have been calculated. However, recent experiments[26] still disagree with the expected numerical estimates from theory within an order of magnitude. The nonlinearity of graphene is remarkably large, however, it needs to be gated to adjust its Fermi level to the resonance conditions. That implies for ungated structures, there is still a tendency to examine other 2D materials as well. Similar discrepancies between measured sheet optical nonlinearity of alternative 2D materials and theoretical estimates are noticed by other researchers as well.
In this work, we present a detailed study of the nonlinear optical properties of 2D transition metal dichalcogenides (TMDCs),[27] with the general formula MX2 with M being a transition metal, here being either Molybdenum Mo or Tungsten W, and X being a chalcogen such as Sulphur S or Selenium Se. Based on a six-band Tight-Binding Hamiltonian, we obtain the nonlinear sheet susceptibility χ(3)2D of the TMDCs through semi-classical perturbation approach.
The semi-classical method retains its validity for low illumination intensities, where Zener tunneling and semimetal transitions could be well ignored and dismissed from the carrier dynamics,[28–30] leaving only multiphoton processes as important. This approximation also is limited by the finite span of optical wavelength and non-zero extent of atomic bonds, that is, the medium has to be effectively treated as continuous and its microscopic granular structure shall be ignored. For ultrashort wavelength optical excitations beyond the deep ultraviolet spectrum, this treatment is no longer valid.
Such nonlinear interactions[31] are of primary importance in study of valley-spin dynamics[32] and Kerr spectroscopy[33] of TMDCs. In all these last works, the TMDC monolayer has been sandwiched in protecting 2D Boron Nitride shields, which has greatly contributed to the visibility and sharpness of emission spectra.[31–34]
The reported data on χ(3)2D of MX2 are very scattered up to four orders of magnitude, as it is shown to be strongly dependent on the growth method and the post-treatment process. This makes a conclusive evaluation out of reach at present. However, we notice agreement roughly within an order of magnitude between the computed numerical figure and the stronger one of the experimental values.
We study the nonlinear optical properties of an ultra\-low-loss amorphous silica microdisk covered by WSe2, and define an effective nonlinear susceptibility 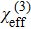
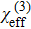
As an application example, we consider the squeezing property of light[36] through four-wave mixing under unpumped and pumped configurations and discuss these scenarios. While calculations reveal the dominance of two-photon absorption over nonlinear Kerr self-phase modulation in 2D TMDCs, we show through detailed theory that an unorthodox π/4-rotated squeezed state of light is produced with an elongated elliptical Wigner distribution and theoretically unlimited squeezing. Without consideration of this π/4-rotation, both quadratures appear to be desqueezed. However, unlimited squeezing is possible only along one π/4-rotated quadrature and the orthogonal quadrature will always be strongly desqueezed.
In order to compute the linear and nonlinear susceptibility from first principles, we would need to have accurate knowledge of the electronic transitions, valleys, and spin-orbit interactions. The correct way to tackle this problem is to have an efficient code to derive the electronic band structure of the material, and since this information is going to be called upon quite frequently inside integration and summation loops, the computation has to be both accurate and very efficient. For this purpose, tight-binding (TB) scheme is very appealing since with correct implementation it could meet both criteria.
The method TB is quite popular for low-dimensional carbon structures such as graphene and carbon nanotubes,[37–38] and six-band TB has been used for studying the band structure of hydrogenated graphane.[39–40] In recent years, two-band[41–43] expansion based on
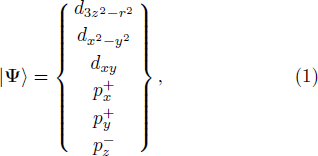
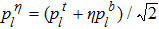
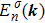
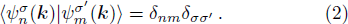
In general for honeycomb lattice with C3v symmetry such as graphene[38] and in absence of chirality, it is normally sufficient to compute the band structure over the irreducible Brillouin zone, which is only 1/12 of the first Brillouin zone. However, monolayer TMDCs are non-centrosymmetric and satisfy a different spatial group denoted as 
The calculated band structures are shown in Fig.
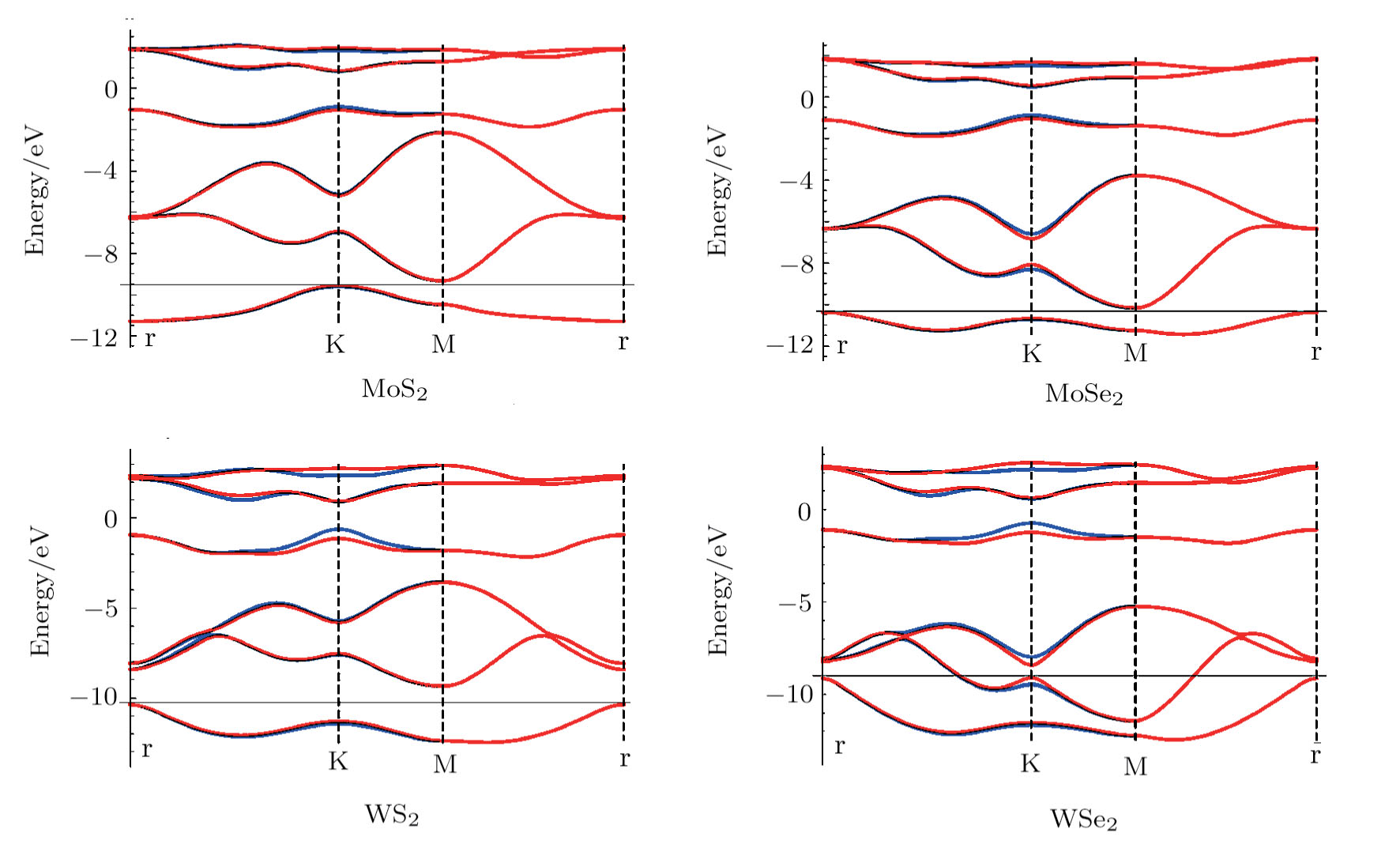 | Fig. 1 (Color online) Band structures of four basic TMDCs, based on the 6-band TB model.[50] Red and blue lines correspond to the spin down and up bands. |
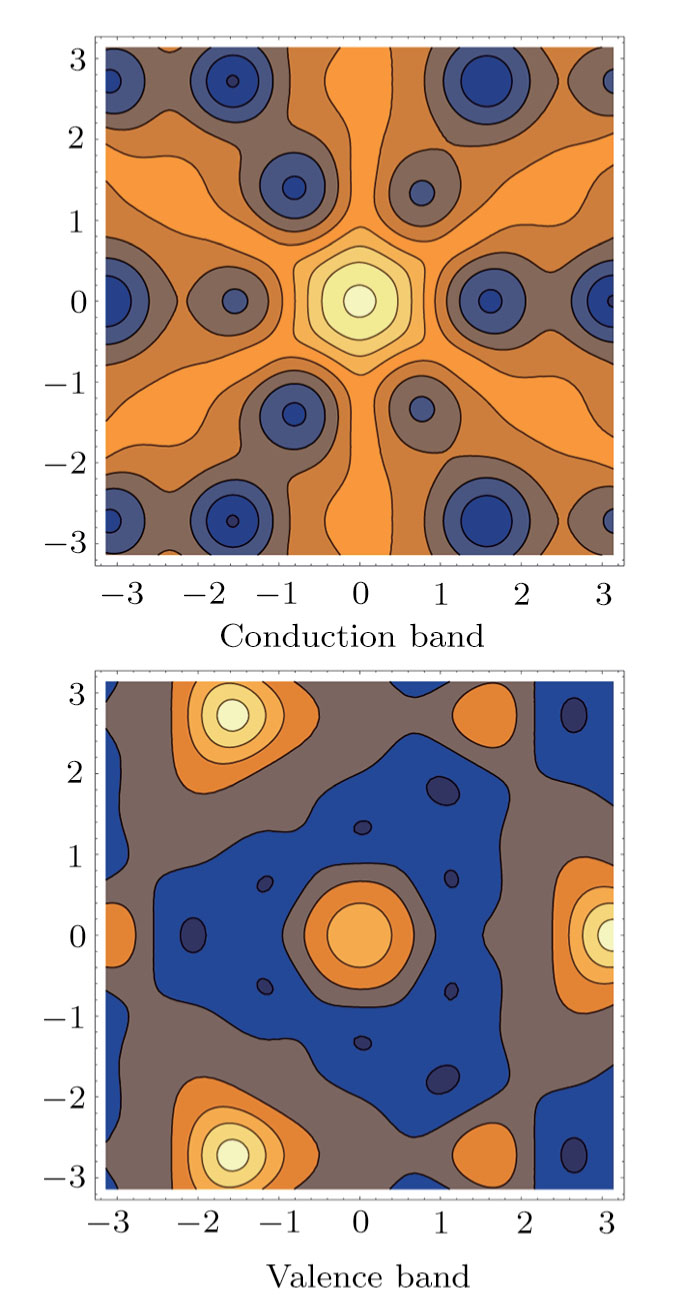 | Fig. 2 Illustration of valley-spin coupling in WSe2 as an example, based on the 6-band TB model.[50] The effect of trigonal warping is seen to be strongly pronounced for the valence band, where K and K′ behave very differently. |
The concept of an interface occupied by a dielectric having finite surface electric and magnetic susceptibilities has been originally investigated in a pair of papers published in 1994.[55–56] Independently and still a few years before celebrated discovery of the first 2D material, graphene, the optical properties, possible modulation and switching applications of such media, referred to as the {conducting interfaces} were explored by a series of papers by the author.[57–62] The transfer matrix method has been reformulated so far independently by many authors to tackle the problem of optical wave refraction from layered structures containing 2D materials[56,58,63–65] and even more recently by Morano[66–67] for measurement of the surface conductivity of graphene.
Based on the theory of conducting interfaces, an ultrathin 2D material could be treated by a discontinuity in tangential electromagnetic fields across the interface. However, the corresponding surface susceptibility or χ2D with the dimension of meter, or equivalently, surface conductivity σs = jϵ0ωχ2D with the dimension of Ω−1 should be known.
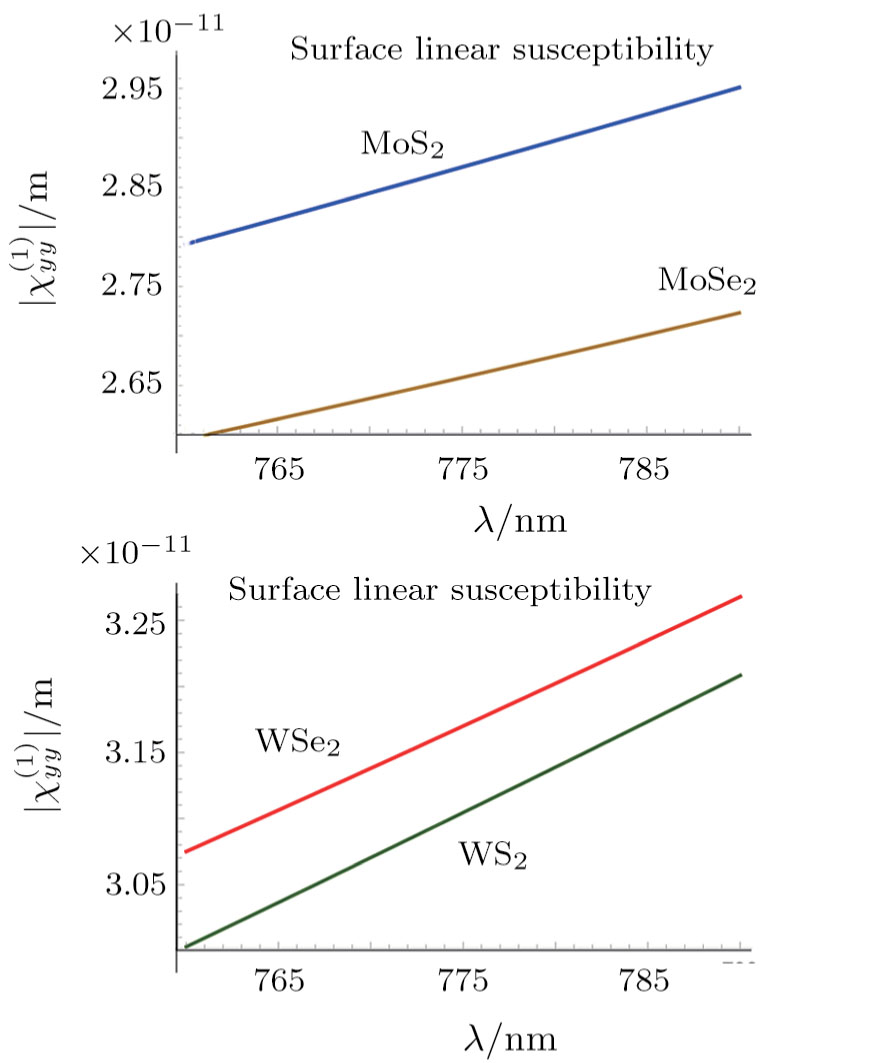
Here, we are able to compute the surface susceptibility tensor elements χ2D(ω) = χ(1)2D(−ω;ω) of TMDCs using the expression
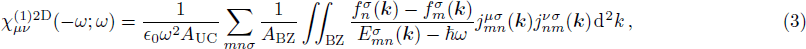
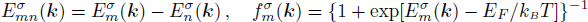
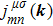
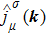
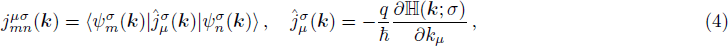
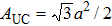
In the third-order nonlinear processes, the location of Fermi-energy has very little observable effect on the Kerr coefficient, and much less on the third-harmonic generation coefficient. This is a fact observed through extensive numerical experiments. Only if the Fermi level is deeply into the conduction or valence bands, that is, the semiconductor is made degenerate, the result would become different. Normally, since chemical doping is not in practice for TMDCs, any shift in the Fermi level would be triggered by electrostatic gating. This method of charge depletion or accumulation, however, is typically unpractical for making a 2D TMDC degenerate. The author believes that there is no practical reason to be concerned about the effect of extrinsic Fermi level as opposed to the intrinsic case with EF = 0.
When the TMDC is not under strain, then linear susceptibility 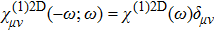
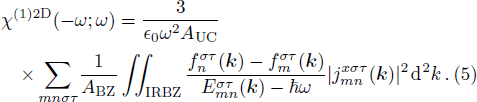
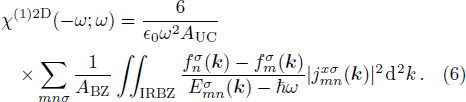
Results of computations for the linear surface susceptibilities of the four basic TMDCs in the wavelength range (760--790) nm is illustrated in Fig.
Folllowing the standard perturbation scheme,[76–88] we have developed a code in Mathematica to compute the non-degenerate four-wave mixing (FWM) third-order nonlinear susceptibility 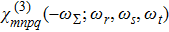
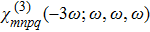
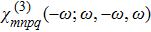
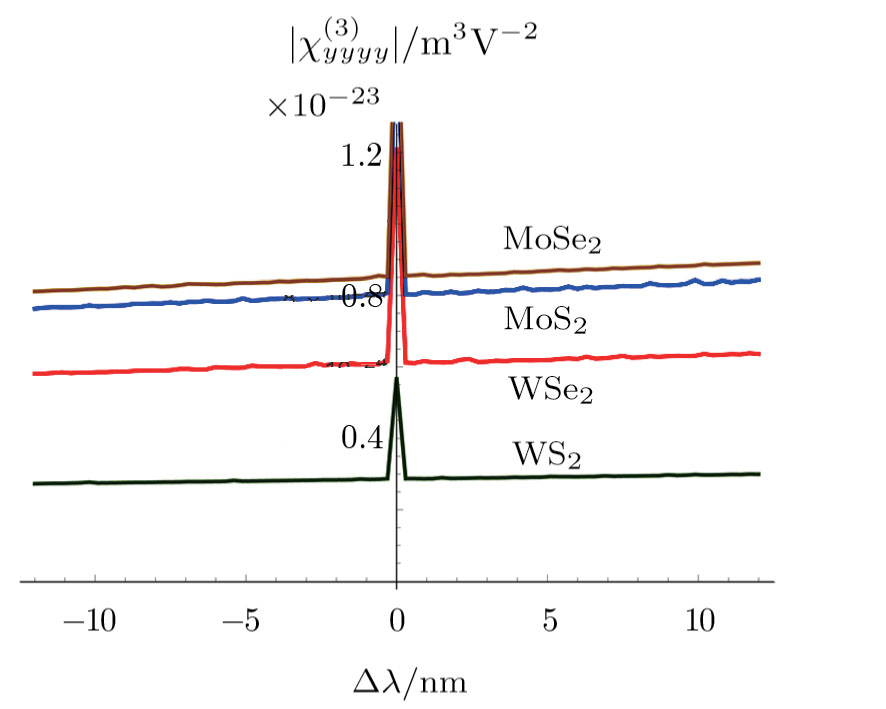
Figure 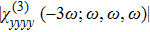
 | Fig. 4 Typical values of third-order nonlinear susceptibility χ(3)(−3ω;ω,ω,ω) for different TMDCs. Contribution to the absolute value is entirely from the real part. |
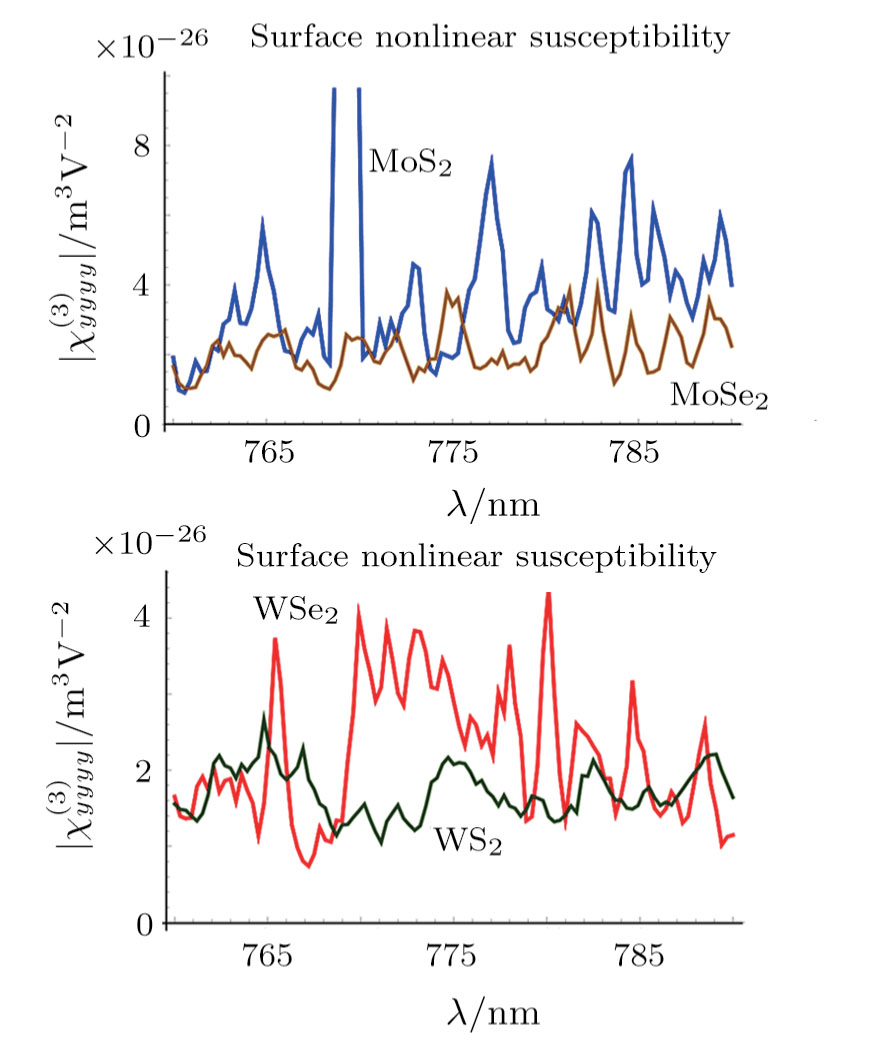
 | Fig. 5 The calculated third-order nonlinear susceptibility χ(3)(−3ω;ω,ω,ω) for MoS2 in the infrared telecommunication window. Contribution to the absolute value is entirely from the real part. |
Resonances in 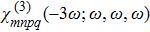
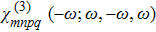
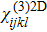
 | Fig. 6 Typical convergence of the code at the wavelength of 1560 nm versus resolution of the computational grid, corresponding to Fig. |
Computations on the Kerr nonlinear susceptibility 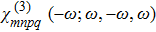
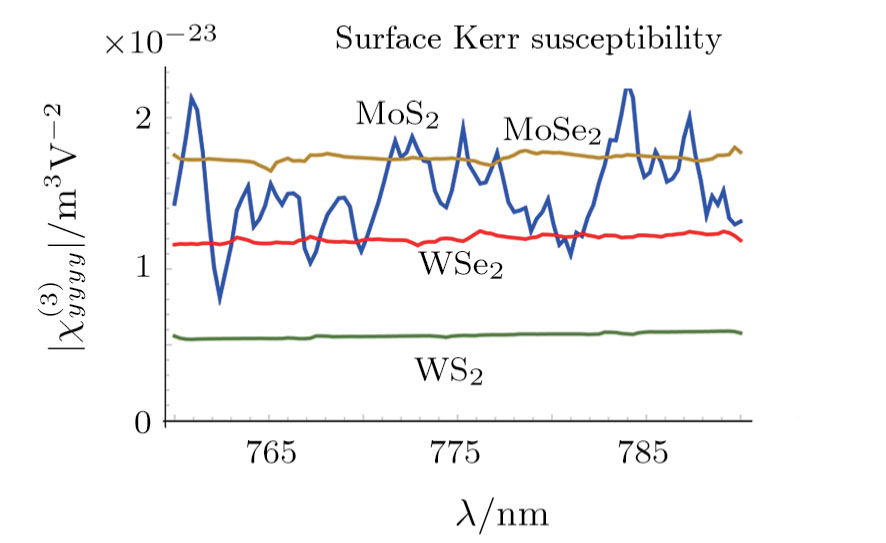 | Fig. 7 Typical values of Kerr nonlinear susceptibility χ(3)(−ω;ω,−ω,ω) for different TMDCs. Contribution to the absolute value is entirely from the imaginary part. |
Furthermore, the magnitude of Kerr nonlinear index is significantly larger than the third-harmonic generation. It is thus to be noticed well that these two parameters of Kerr nonlinearity and third-harmonic generation, although related, but are essentially much different in both their physics and behavior. Actually, these two values could be quite far apart in phase and many orders in magnitude.
We here point out again that the Kerr nonlinear susceptibility χ(3)(−ω;ω,−ω,ω) and Third-harmonic generation susceptibility χ(3) (−ω;ω,ω,ω) are not the same. While both are having the third-order, these correspond to entirely different processes. This difference can be understood as follows.
The Kerr nonlinear susceptibility only describes a process in which the local permittivity of the medium is linearly dependent on the local intensity of light, such as 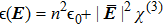
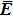
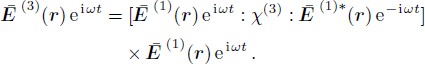
However, the third-order nonlinear susceptibility directly is connected to the local amplitude of the harmonic, as a result of locally present electromagnetic field. Hence, one could imagine that the third-harmonic be related to the first harmonic as
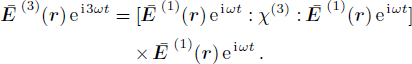
Since the physical phenomena behind these two mechanism are not identical, one would naturally expect that χ(3)(−ω;ω,−ω,ω) ≠ χ(3) (−ω;ω,ω,ω). Sometimes, this fact is not sufficiently made clear in the literature.
(i)
Defining a critical electric field as 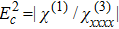
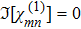
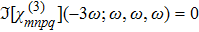
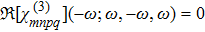
(ii)
In this wavelength range of interest and for the linear response, the typical strength of linear susceptibility χ(1) is within the range of (3.5’4.4) × 10−8 m, so that having an effective monolayer thickness of t2D we may assign an effective refractive index of 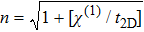
Referring to Fig.
This places the expected nonlinearity of 2D TMDCs, to many orders of magnitude stronger the range of III-V semiconductors such as GaAs 1.4 × 10−22 m2 · V−2, and than that of Diamond 2.5 × 10−21 m2 · V−2, fused silica 2.5 × 10−22 m2 · V−2, and even GaP at 577 nm 2.93 × 10−18 m2 · V−2,[80] which is known to have an extremely large nonlinear index of refraction.
We first define a bulk-equivalent susceptibility as 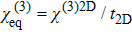
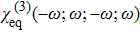
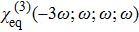
These numbers could reasonably well explain the recently observed ultrastrong high harmonic generation in 2D TMDCs.[76,91–92] There are certain classes of materials or media, which could offer significantly stronger nonlinearity, however, either their slow response times (such as polymers) or complexity of formation (such as cold atomic gases), render them of limited use at optical frequencies.
The unusually large nonlinearity of 2D materials compared to bulk 3D structures is hard to explain. However, we believe that it is a matter of geometrical confinement dimensions that sets this strength. At least it has been rigorously established that the third order nonlinear optical response of spin density wave insulators is much stronger in 2D than 3D and 1D structures.[93]
(iii)
The validity of numerical results could be furthermore verified against three recent experimental data[76,91,94] on 3rd harmonic generation from MoS2 at the wavelength of 1560 nm. While our developed code estimates a value of 1.6 × 10−25 m3 · V−2 for 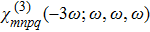
This shows that while experimental results[76,91,94] vary within four orders of magnitude, our numerical estimate is much closer to the first measurement[76] reporting the larger value. The difference between theoretical results with experimental ones, therefore, should not be surprising considering the remarkably scattered numerical values among experimental observations. While the nature of such differences is not exactly known yet, it could be due to material growth and transfer issues, defect concentrations, substrate effects, as well as the optical method of measurement. Given the large sensitivity of TMDCs to the fabrication process and even resilience under ambient conditions, there remains a question of how to unify experiments alike. It could be speculated that for a variety of reasons, the experimental reports actually either underestimate or overestimate the nonlinear susceptibility over the true theoretical value.
(iv)
With regard to the individual tensor components recognized by the set of indices μνζη, there should be 24 = 16 elements. However, half of them are zero and the only non-zero tensor elements are yyyy, xxxx, xyxy, yxyx, xyyx, yxxy, xxyy, and yyxx. Even though, all tensor elements are not quite independent and the following identities hold for all four TMDCs due to the crystal symmetries
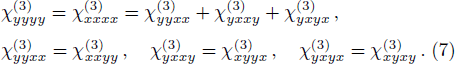
For the case of Kerr nonlinearity where the parameter 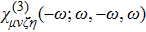
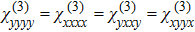
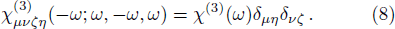
Similarly, we could write for the third-harmonic generation the following
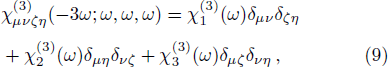
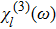
In this section, we discuss production of a non-classical state of light with elliptical Wigner distribution, due to two-photon absorption. Since the method of analysis is based on the theory of squeezing, we need to initially present an overview of light squeezing schemes.
Squeezing of light is usually done through either of the following general methods:[96–102]
(i) Squeezed light by parametric down conversion.
(ii) Squeezed light in optical fibers.
(iii) Squeezed light in atomic ensembles.
(iv) Squeezed light in semiconductor lasers.
Out of the above four methods, the first three are mostly implemented in a non-monolithic experiments and normally require large optical setups. The second one is based on the χ(3) effect of fused silica in optical fibers, and thus requires long propagation paths over fibers to achieve squeezing, but squeezing as large as 9dB has been achieved using this scheme. The third one requires sophisticated techniques of atom vapor trapping and condensation at ultralow temperatures, and the largest observed squeezing of 13dB has been so far achieved this way. The fourth method[103] is relatively easy to achieve and based on monolithic integrated photonics, but is limited for various practical reasons to only 3-4dB of reduction in shot noise and thus squeezing.
Recent advances in optomechanics, has brought the possibility of optomechanical squeezing of light into perspective as well.[104–109] Optomechanical squeezing of light in homodyne detection within a small amount also occurs, and can be observed using a novel quantum feedback control scheme, which has been recently reported.[110] Monolithic approaches to squeezing by optical parametric oscillators[111] have been shown to be feasible as well.
As an alternative route, the possibility of using Si3N4 micro-ring resonators for squeezing has been demonstrated in a multi-mode optical parametric oscillator[112] with 1.7 dB squeezing. This has also apparently been verified experimentally at room temperature by pumping a continuous laser,[113] and 0.5 dB squeezing below shot noise was observed in a self-homodyne setup. So, it could be safely claimed that using silica microdisks covered with 2D TMDCs, certainly measurable squeezing could be obtained. It has been furthermore recently shown that high-quality silica micro-ring resonators could provide a versatile platform for study of emission properties of 2D materials.[35]
It is known that the 3rd order nonlinearity could be employed to generate squeeze light. Depending on the optical setup, that whether the squeezed state is produced through unitary transformation in vacuum, or an interferometric setup, it leads to either of the Hamiltonians[114–115] as
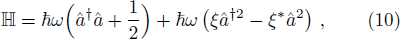

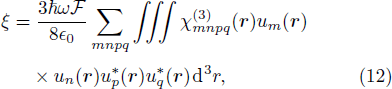
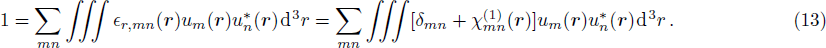
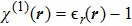
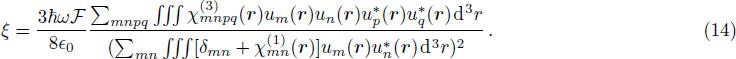
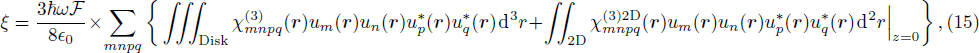
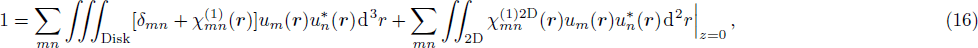
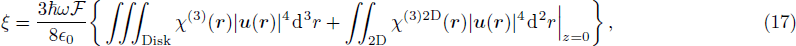
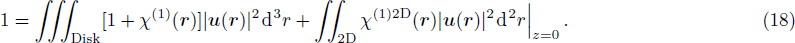
(i)
Alternatively, Eq. (

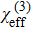
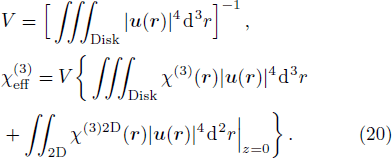
It should be mentioned here that ξ and therefore 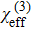
Another way to look into this is to view the circulating optical power in disk resonator as an optical field going through a long straight path,[119–120] thus experiencing an overall phase retardation. This is the basis of light squeezing in optical fibers,[121–124] and this point of view gives a more clear and straightforward measure for the squeezing parameter s as
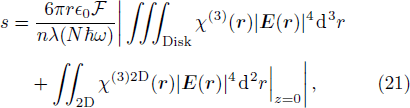
Now, plugging in Eq. (
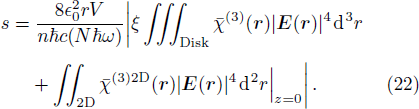
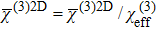
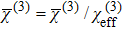
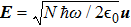

(ii)
As it was discussed in the above, χ(3) is purely imaginary in the wavelength range of interest between 760 nm to 790 nm, and thus it is the two-photon absorption, which wins over the Kerr nonlinear index. Despite this fact, this is unimportant for our particular application of producing a non-classical state of light with non-circular Wigner distribution.
Some studies have only considered the absolute value of |χ(3)| to the squeeze parameter s = |ζ|,[121] where ζ is the complex squeeze parameter given by the squeeze operator as[97,121,125–127]
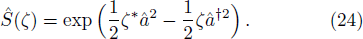
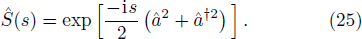
It should be mentioned that actual ratio of noise squeezing for the case of Eq. (
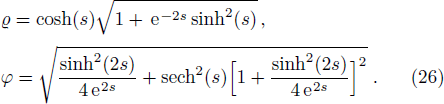
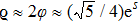
As it has been demonstrated in the Appendix 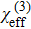
One therefore may produce a non-classical light using a micro-disk resonator covered with a 2D TMDC, such as WSe2, or MoS2. We would like to investigate this possibility by taking advantage of the very large χ(3) coefficient of 2D TMDCs. Combined with the very strong confinement of light in low loss silica disk resonators, we would expect a significant anharmonicity ξ as defined in Eq. (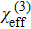
(i)
A possible advantage of this scheme in case of successful design and experiments, would be relatively ease of fabrication and operation, as well as compatibility with monolithic integrated photonics. Usage of ultrashort solitons[128–129] together with strong confinement in micro-disks increases the overall nonlinear interactions and thereby squeezing as well. This has been already demonstrated in squeezing via optical fibers.[96] In that case, no extra pumping is needed, and the pulse undergoes squeezing by itself through self-pumping. Evidently, the squeezed output is pulsed. Since the quality factors of cavities is not infinite, a small dissipation at high optical power densities is unavoidable,[118,130–133] which can be treated anyhow as either a Lugiato-Lefever equation[134] or using a perturbative expansion.[135]
(ii)
It is in practice beneficial if the optical power required for excitation of nonlinearity is maintained by a pump held at a slightly different frequency such as ωp = ω ± FSR, where FSR is the free spectral range of the micro-disk resonator. The susceptibility then should be calculated from the non-resonant near-degenerate pumped value χ(3)(−ω;ωp, −ωp,ω). Since FSR ≪ ω, then χ(3)(−ω; ωp, −ωp,ω) stays within the same order of magnitude of χ(3)(−ω;ω,−ω,ω), thus leaving the presented analysis and discussions basically intact. A closely related scheme with two pumps with frequencies 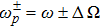
A numerical evaluation of near-degenerate χ(3)(−ω; ωp, −ωp, ω), as shown in Fig.
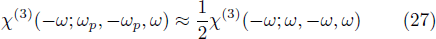
This scheme, as opposed to the ultrashort solitons, enables continuous pumping and signal feeding, and therefore a continuous squeezed output may be expected as well.
Without doubt, the prominent role of excitons in light emission from TMDCs could be considered as a subject of deep study. This is due to the fact that all of the four basic types of TMDCs discussed in this paper support both of the dark and bright excitons, which is further complicated by the trignoal warping property of these materials and presence of charged excitons (also known as trions) and biexcitons.[35, 138–139]
In general, exciton binding energies in 2D materials cannot be explained by a simple hydrogenic model, because of the very different radial distribution of the wavefunction, which could easily be extend to a few nm in radius. It only can be investigated by DFT GW-BSE calculations, which exhibits numerous lines between 1s and 2p states. While the exciton binding energies in 2D materials can be large, these are directly dependent on the substrate screening effects. When there are insulating encapsulation or separation, for instance, using bilayer graphene (or BN in other works), the exciton binding energy may drastically reduce by a factor of 3 to 6.
At room temperature, exciton emission peaks are significantly broadened, because of large electron-phonon coupling rates in typical TMDCs. Biexcitons in 2D materials are unstable at room temperature and dissociate, since their binding energies are on the order of only a few meV. The exciton-exciton annihilation (EEA), which is a four-particle process can occur under high exciton population (demanding high illumination intensities) in principle even at the room temperature, but it can be expected that at such high rates, non-radiative recombinations through defect states and impurities would be dominant over the entire EEA process. Dark excitons in most 2D materials can actually emit light. Since they are optically forbidden because of vanishing dipole. However, the true dipole should be complex valued instead of a real one, so that they can emit non-linearly polarized light (not necessarily exactly circular). The fact that the energy different between dark and bright excitons is on the same order of exciton binding energy complicates the correct interpretation of light emission.
While the existence of biexcitons at room temperature is unlikely because of the small binding energy, there are strong reasons to believe that emission from charged excitons could be easily mistaken with defect emissions because of interface effects.[32,140–141] Quite possibly, the existence of higher-wavelength emission peaks in photo-luminescence spectra of TMDCs could be due completely due to interface defects, and in that case trions/biexciton emissions can have no influence at room-temperature as they normally appear only at cryogenic conditions.[142] If ture, then the observed trion emission peaks could be actually a defect-related emission, and for this reason is entirely absent in boron-nitride (BN) encapsulated monolayer TMDCs.[32,142] Similarly, there exists experimental evidence for brightened dark excitons/trions in WSe2, where measurements are all done at low temperatures.[143]
Another recent study[144] is citing the fact that the two emission peaks for MoS2 on thermally grown SiO2, correspond to A-exciton and interface Defect. The defect state disappears at room temperature, which is somehow connected to observations reported in Ref. [32]. Furthermore, they propose an elegant way to identify a defect state.
The emission of a defect is almost always unpolarized regardless of the pump incidence angle, intensity, and polarization, and that is why it cannot form polaritons in cavity quantum electrodynamics (CQED) experiments. A careful polarization measurement on the emission spectra could unanimously reveal whether the lower energy peak is a defect or excitonic emission.
In summary, the origin and nature of peaks in the emission spectra of TMDCs has been a matter of unresolved debate[32,140–157] and still remains with no conclusive agreement so far.
We have presented a detailed theoretical analysis of linear and third-order nonlinear optical response of two-dimensional (2D) monolayer transition metal dichalgonides (TMDCs). Based on a rigorous six-band tight-binding model, we have calculated first order and third order susceptibility tensors, and observed reasonable consistency with experimental data. We predict an elongated non-classical light using high quality silica micro-disk resonators covered with the monolayer TMDCs.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] | |
| [74] | |
| [75] | |
| [76] | |
| [77] | |
| [78] | |
| [79] | |
| [80] | |
| [81] | |
| [82] | |
| [83] | |
| [84] | |
| [85] | |
| [86] | |
| [87] | |
| [88] | |
| [89] | |
| [90] | |
| [91] | |
| [92] | |
| [93] | |
| [94] | |
| [95] | |
| [96] | |
| [97] | |
| [98] | |
| [99] | |
| [100] | |
| [101] | |
| [102] | |
| [103] | |
| [104] | |
| [105] | |
| [106] | |
| [107] | |
| [108] | |
| [109] | |
| [110] | |
| [111] | |
| [112] | |
| [113] | |
| [114] | |
| [115] | |
| [116] | |
| [117] | |
| [118] | |
| [119] | |
| [120] | |
| [121] | |
| [122] | |
| [123] | |
| [124] | |
| [125] | |
| [126] | |
| [127] | |
| [128] | |
| [129] | |
| [130] | |
| [131] | |
| [132] | |
| [133] | |
| [134] | |
| [135] | |
| [136] | |
| [137] | |
| [138] | |
| [139] | |
| [140] | |
| [141] | |
| [142] | |
| [143] | |
| [144] | |
| [145] | |
| [146] | |
| [147] | |
| [148] | |
| [149] | |
| [150] | |
| [151] | |
| [152] | |
| [153] | |
| [154] | |
| [155] | |
| [156] | |
| [157] | |
| [158] | |
| [159] | |
| [160] | |
| [161] | |
| [162] | |
| [163] | |
| [164] | |
| [165] | |
| [166] | |
| [167] |