† Corresponding author. E-mail:
Wave properties of solitons in an unmagnetized four-component dusty plasma system contains isothermal distributed electrons, mobile ions, and negative-positive dusty grains have been examined. To study DIA wave properties, a reductive perturbation (RP) analysis is used. By a reductive perturbation (RP) analysis under convenient coordinate transformation, the three dimension Kadomtsev-Petviashvili equation in cylindrical coordinates is obtained. The effects of dust grain charge on soliton pulse structures are studied. More specifically, solitary profile depending on the axial, radial, and polar angle coordinates with time is discussed. This investigation may be viable in plasmas of the Earth’s mesosphere.
No doubt, studying of nonlinear waves and their structures in plasmas with charged dust grains is one of important activities during the last few decades for explaining many systems in astrophysics (Earth magnetosphere, cometary tails, nebulas, mesosphere),[1–4] as well as in the laboratory.[5–6] Moreover, it has remarkable applications in fiber optics, plasmas of semiconductor, and dust-crystals.[7–9] The charged grains in plasmas change plasma features, and define new types of wave phenomena.[10–13] Many investigations are made to expound the applications of nonlinear properties in astrophysics and space dust plasmas.[14–16] It has been reported that dusty grains in multicomponent plasmas influenced the collective interactions in plasmas[17] and the variation of dust charge modified shock features.[18–20] Many articles discussed the negative dusty plasma applications in space.[21–22] On the other hand, in other studies, both negative-positive grains are taken into account in space plasma[23–24] and in plasma laboratories.[25] On the other hand, a new dust grain model has been approached for cometary plasmas having opposite charges polarity in the depletion of electrons and ions.[26] Later, plasma containing ions, electrons, grains with positively-negatively charged was inspected.[27] It was investigated that, new positively grain component caused the existence of twofold solitary potentials. Furthermore, shock behavior in inhomogeneous plasmas with ionizing source is examined.[28] They reported that, charge polarity fluctuation of dusty charge improved the monotonic characteristics of shock waves. However, many of these studies are regarded to the unbounded planar geometry. This is not true for space and laboratory plasma. So we have taken the non-planar form of cylindrical geometry into account. Several theoretical studies in non-planar geometry on the dust plasmas features have been deliberated.[29–32] A multidimensional cylindrical form of Kadomtsev-Petviashvili equation (CKP) in dusty plasmas with two superthermality distributed temperature ions has been introduced.[32] Finally, El-Bedwehy et al. investigated CKP equation in a plasma of two charged dust grains.[33] They examined features of soliton formation that depends on with the polar, radial and axial coordinates.
Our article is to explore the non-planar (cylindrical) three-dimensional DIAWs in four components dust plasma system contains isothermal electrons, mobile ions and negative-positive dust grains. We study the effects of ion to electron number density ratio, negative dust grain to electron density ratio and positive grain with an electron number density ratio on nonlinear wave phase speed as well as on the pulse width and amplitude. In addition, the effect of non-planar geometry on the pulse profile is studied. The organization of this paper is as follows. In Sec.
Consider a three-dimensional, unmagnetized dusty plasma system whose constituents is isothermal distributed electrons, mobile ions, negative and positive dusty grains. The three-dimensional continuity equations for mobile components are given by
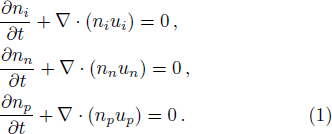
The corresponding momentum equations are,
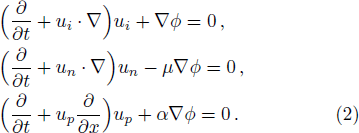
These equations are supplemented by Poisson’s equation:
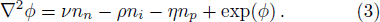
In the above equations nj (j = i,n,p,e) are the perturbed number densities and ni0, nn0, np0, and ne0 are the related equilibrium values. Also uj (j = i,n,p) are the ion, negative and positive dusty plasma velocities, respectively, normalized by the ion sound velocity (KBTe/mi)1/2, ϕ is the electrostatic potential and normalized by (KBTe/e), time variable t and space coordinate are normalized by inverse of the plasma frequency 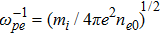
From the charge neutrality condition, we have

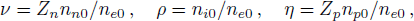
To study DIA wave properties, a reductive perturbation (RP) analysis is used.[34] We introduce the new independent variables:[35–36]
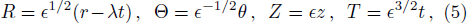
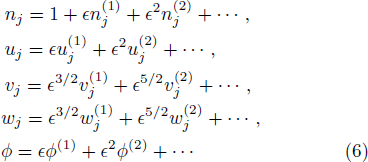
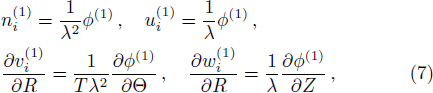
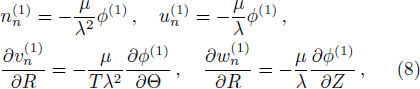
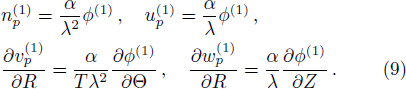
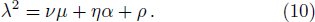
At the next order in ε, the evolution equation for the first order perturbed electrostatic potential in the form
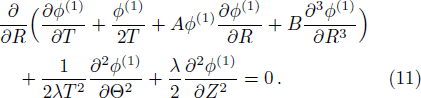
The nonlinear and the dispersion coefficients A and B are given by
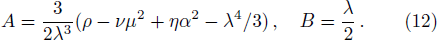
Equation (
In order to solve Eq. (
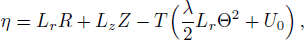
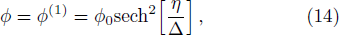
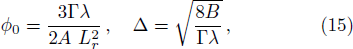
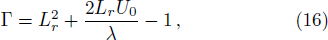
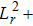
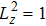
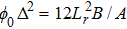
To carry out this study, many conditions are introduced (i) for model components, our assumption is isothermal electrons and cold fluid of ions and dust grains[38] (ii) the gravitational effect is neglected for submicron dusty grains[38–39] (iii) the plasma is of low coupling parameter (iv) inter-grain distance is very small. By applying reductive perturbation theory, introduced by Taniuti and Wei (1968),[34] this plasma model leads to a 3D-CKP equation (
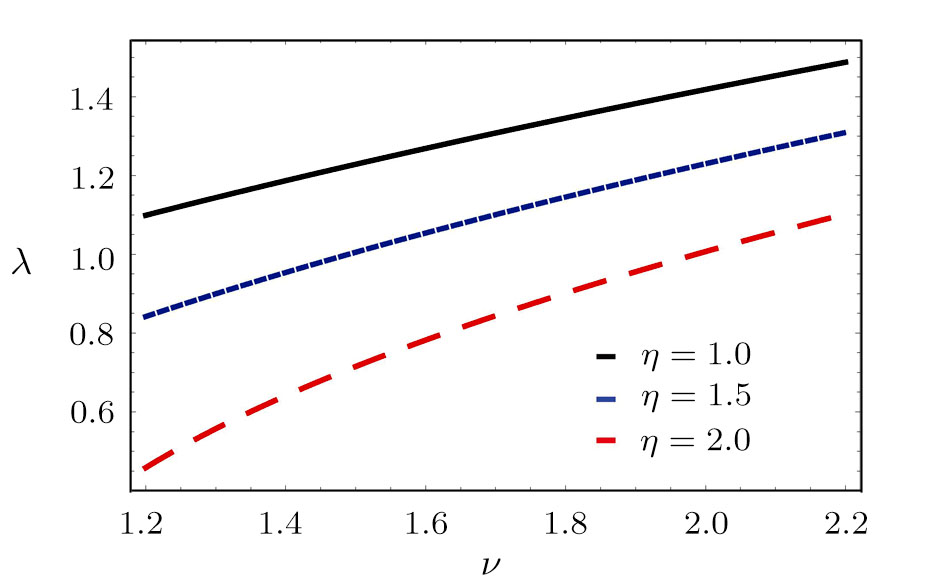
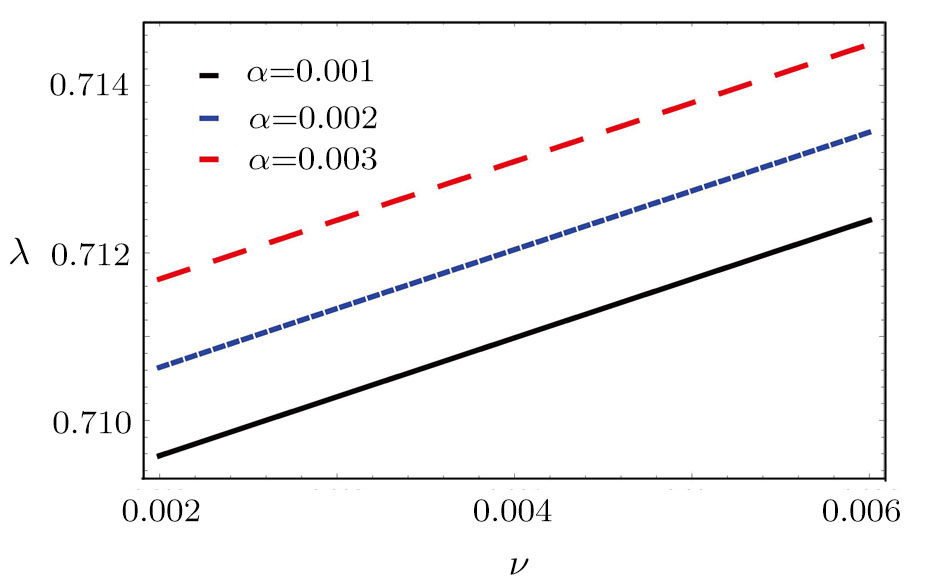
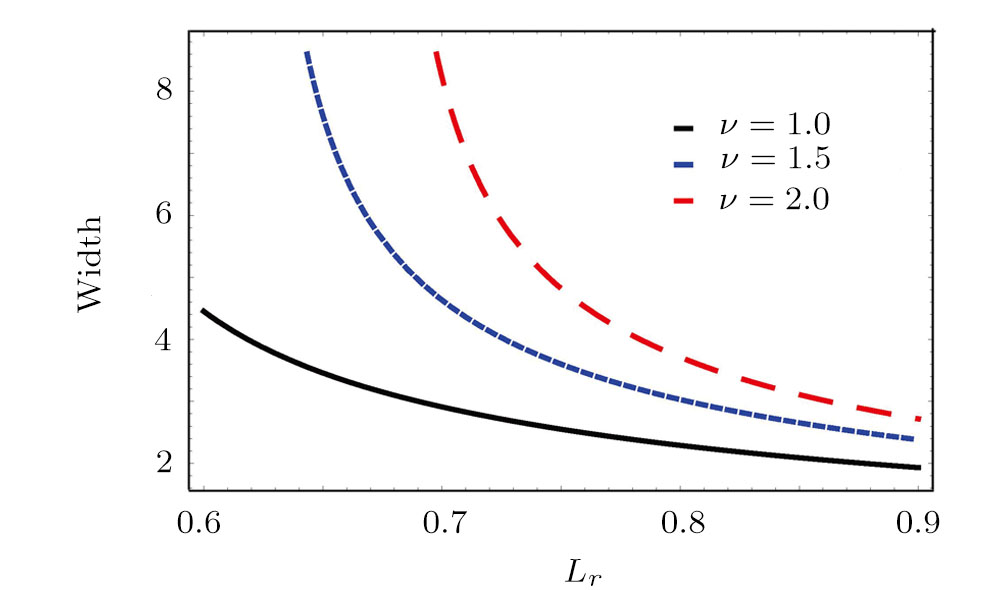
Figure
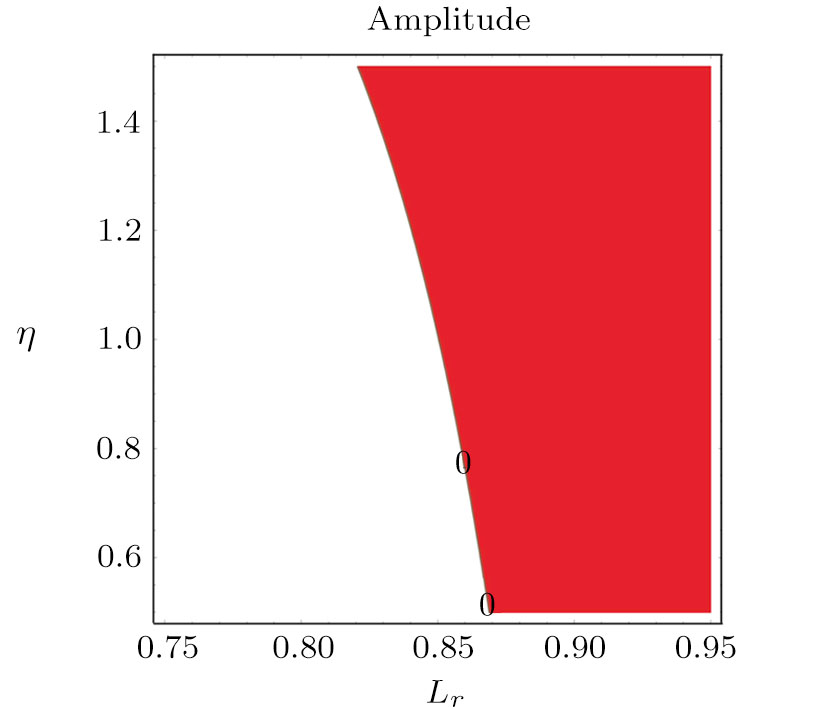
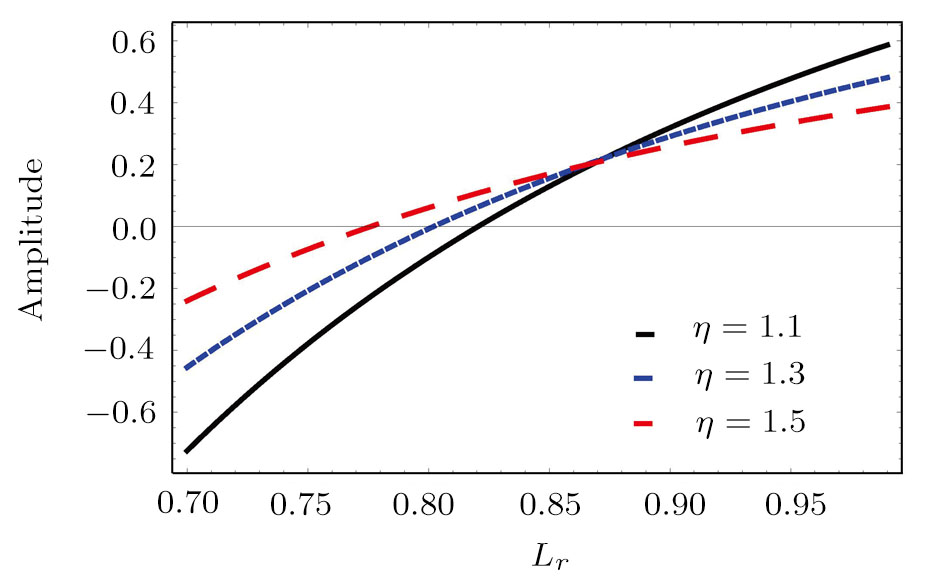
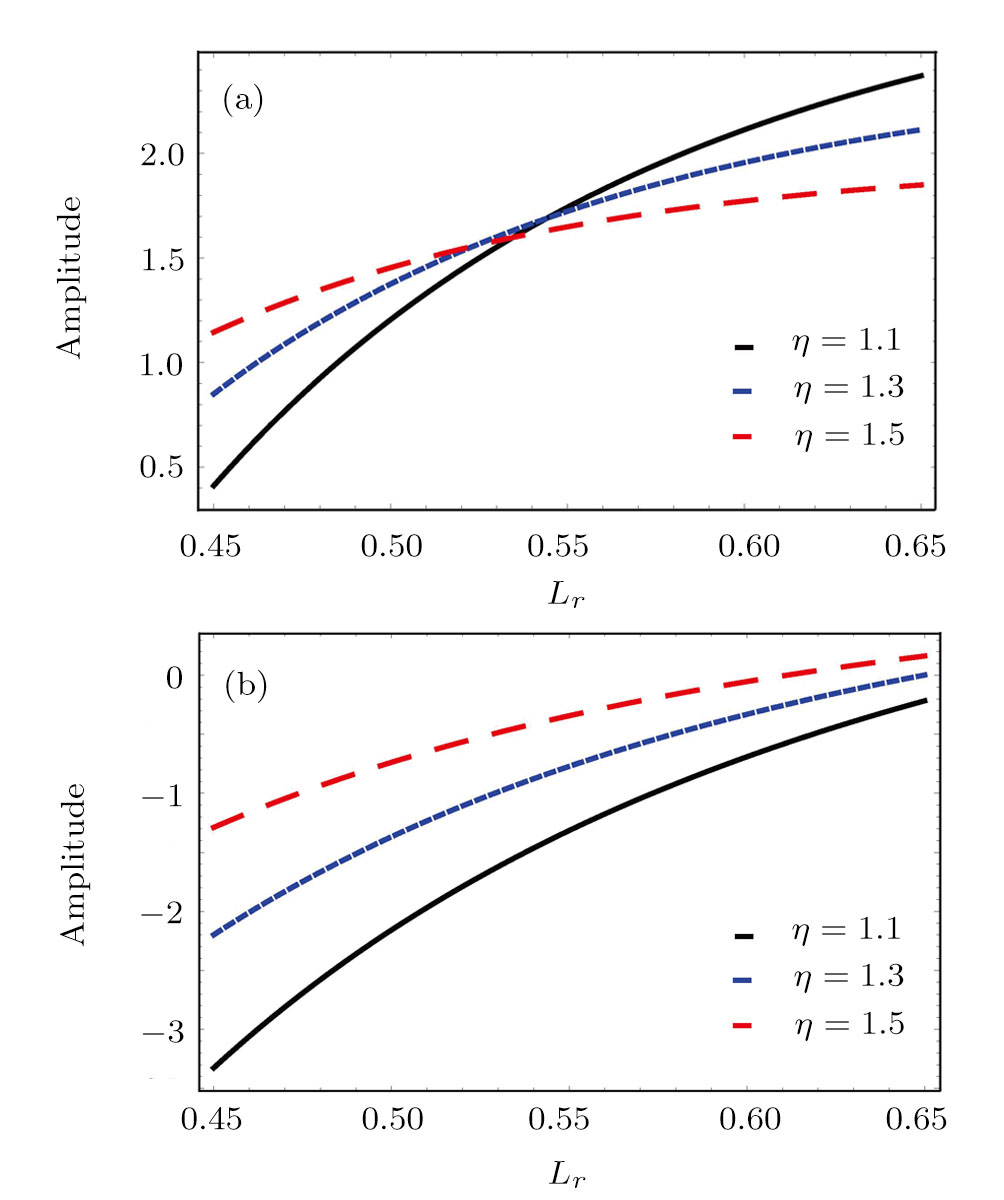 | Fig. 5 Change of amplitude ϕ0 against Lr and η for α = 0.002, μ = 0.005, ν = 1.1, and (a) U0 = 0.95; (b) U0 = 0.4. |
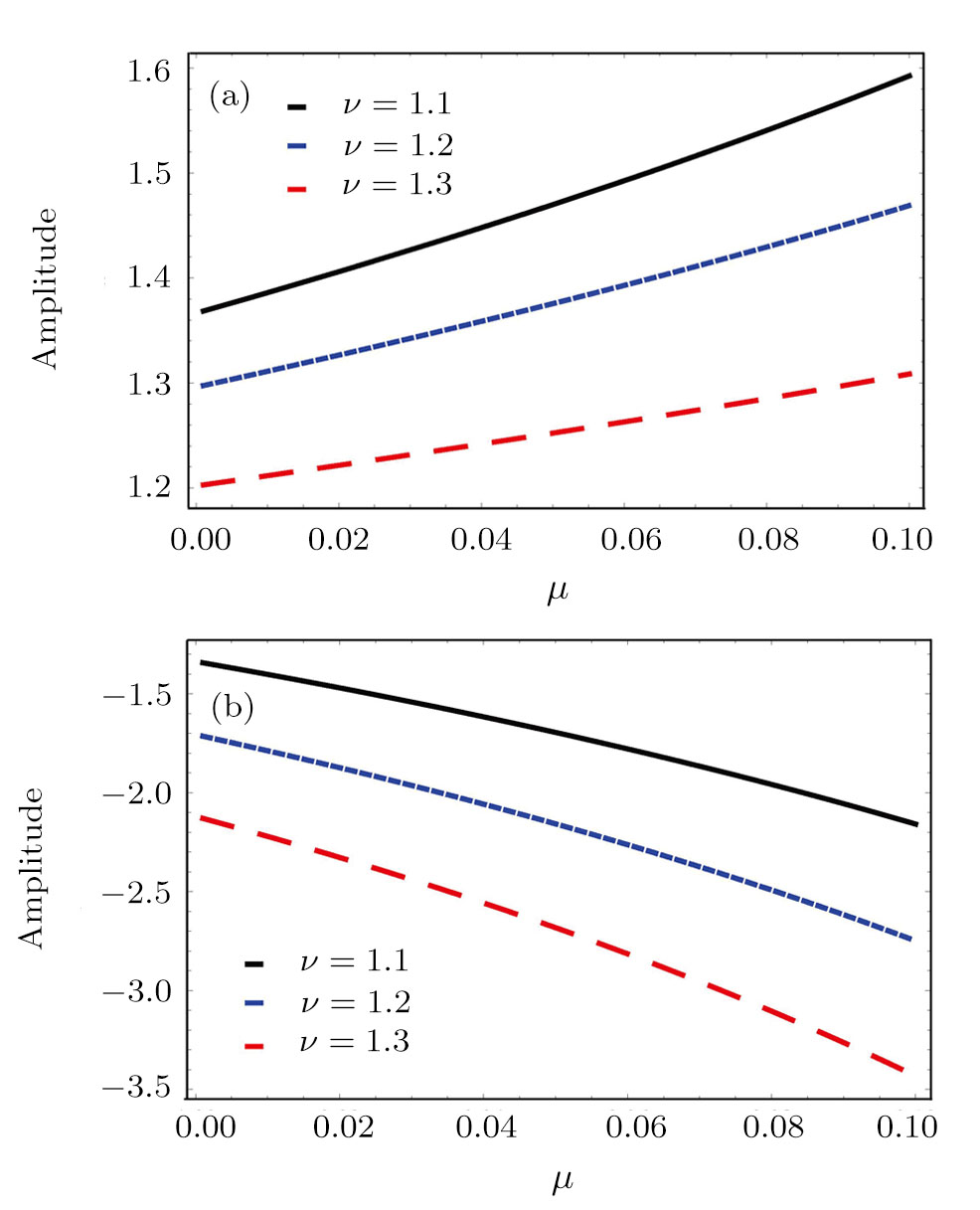 | Fig. 6 Change of the amplitude ϕ0 against μ for different values of ν and for α = 0.002, Lr = 0.5, η = 1.3, and (a) U0 = 0.95; (b) U0 = 0.4. |
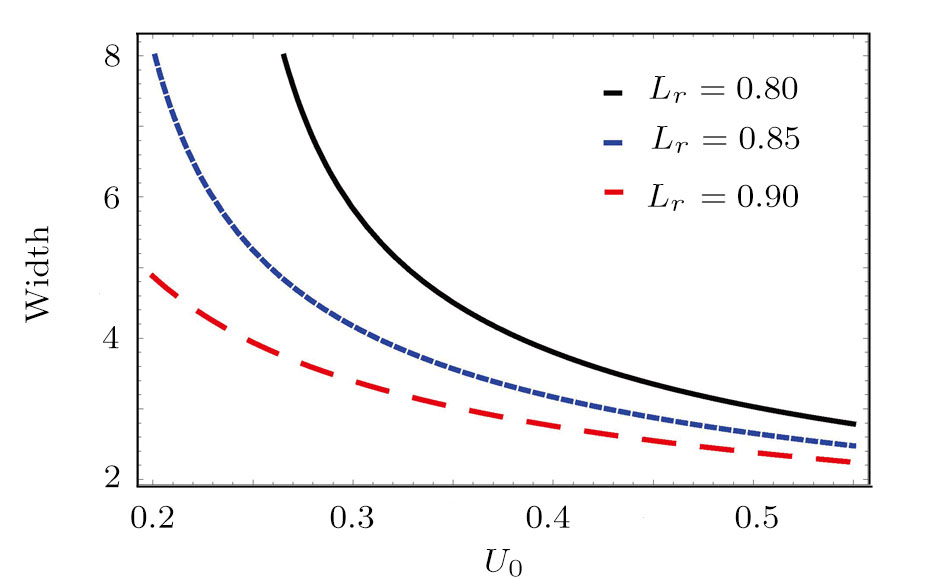 | Fig. 8 The change of the width Δ against U0 for different values of Lr and for α = 0.002, μ = 0.005, ν = 1.5, and η = 1.5. |
On the other hand, Figs.
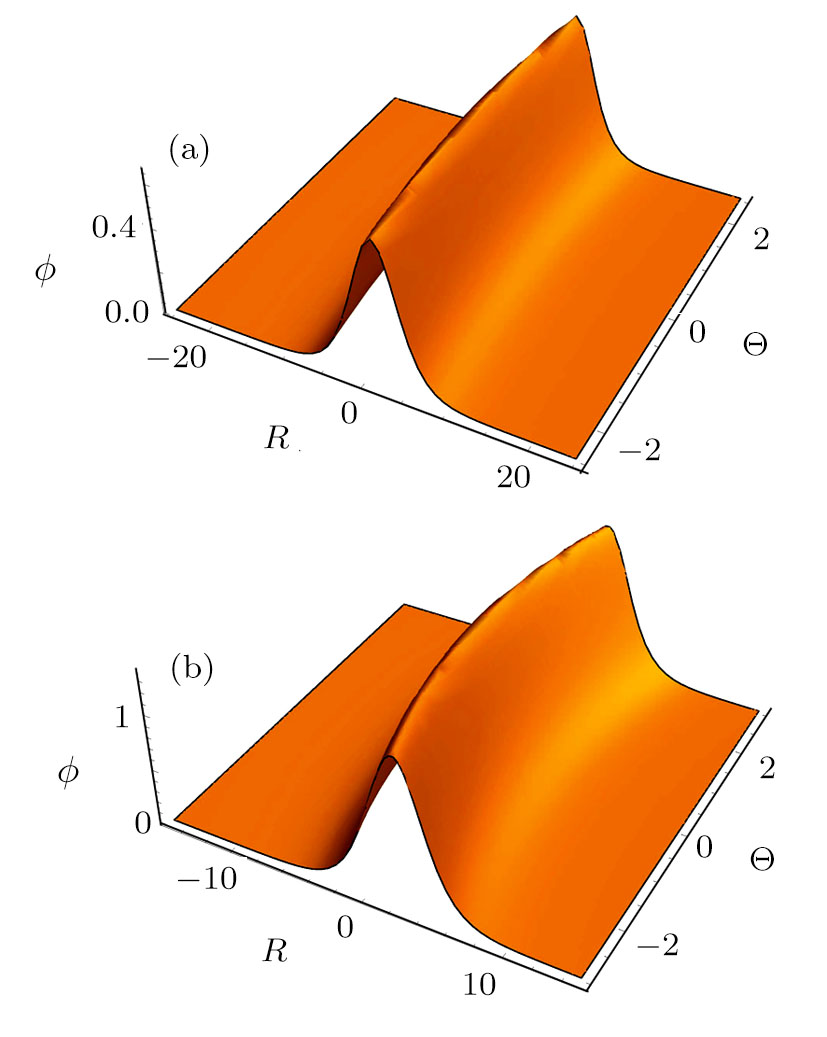 | Fig. 9 Three-dimensional solitary wave profile ϕ ( |
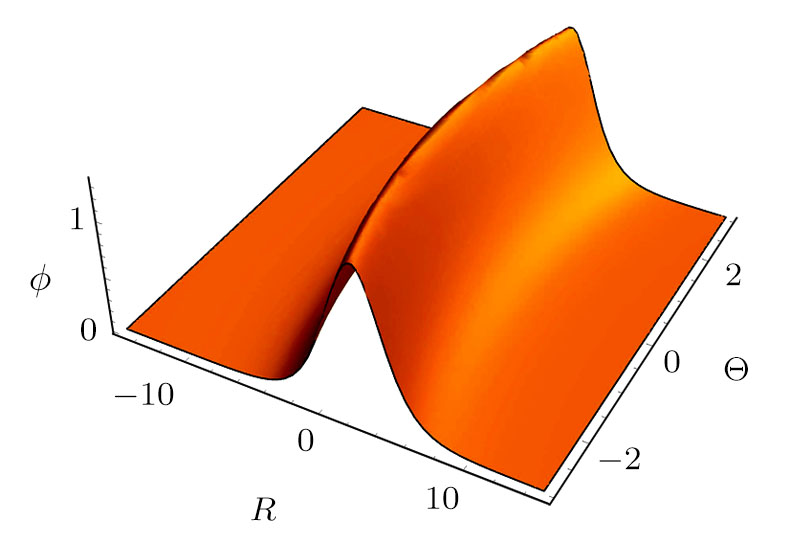 | Fig. 10 Three-dimensional solitary wave profile ϕ ( |
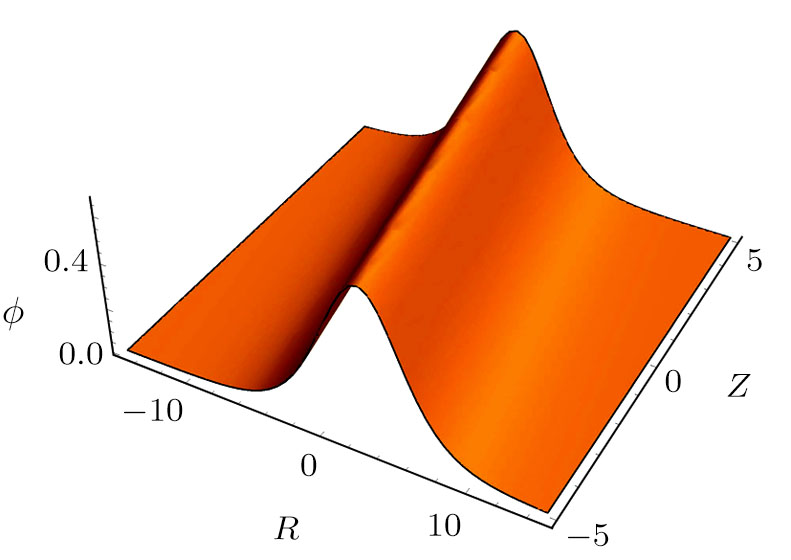 | Fig. 11 Three-dimensional solitary wave profile ϕ ( |
Summing up, we have studied DIASWs propagation in plasma with isothermal electrons, mobile cold ions, positive and negative dust grains considered cylindrical geometry. The angular and radial dependence have been considered. Employing the (RP) technique, a 3D-CKP equation which describes the evolution of DIASWs has been derived and its localized solution has been obtained by reducing the 3D-CKP to the Korteweg-de Vries equation on employing a simple transformation of the coordinates. The effects of system parameters (ν, η, μ, Lr and U0) on phase velocity λ, soliton amplitude ϕ0, and width Δ have been examined numerically. We have shown graphically that these parameters play a vital role in the formation and the features of the DIA mesospheric solitary waves.[38,46–47] These results agree with the mesospheric plasma information, see Refs. [46–47]. Finally, our investigation of the solitary wave properties could be important in understanding nonlinearity features in space, as well as in laboratory and astrophysical environments in mesospheric plasma.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] |