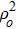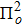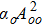† Corresponding author. E-mail:
This paper presents an investigation of self-focusing of a quadruple Gaussian laser beam in collisionless magnetized plasma. The nonlinearity due to ponderomotive force which arises on account of nonuniform intensity distribution of the laser beam is considered. The nonlinear partial differential equation governing the evaluation of complex envelope in the slowly varying envelope approximation is solved using a paraxial formalism. The self-focusing mechanism in magnetized plasma, in the presence of self-compression mechanism will be analyzed in contrast to the case in which it is absent. It can be observed that, in case of ponderomotive nonlinearity, the self-compression mechanism obstructs the pulse self-focusing above a certain intensity value. The effect of an external magnetic field is to generate pulses with smaller spot size and shorter compression length. The lateral separation parameter and the initial intensity of the laser beam play a crucial role on focusing and compression parameters. Also, the three-dimensional analysis of pulse propagation is presented by coupling the self-focusing equation with the self-compression one.
The interaction of intense electromagnetic waves with plasma has been of considerable interest due to its significance in number of applications such as plasma based beat-wave accelerators,[1] plasma-based accelerators,[2] inertial confinement fusion,[3–4] ionospheric modification,[5–7] laser charge particle accelerator,[8–9] and X-ray lasers.[10] The success of these applications depends on propagation of laser over several Rayleigh lengths while maintaining the efficient interaction with plasma. Pulse focusing and pulse compression have been proved to be an effective way of guiding a laser pulse in the medium over many Rayleigh lengths and to increase radiation power and intensity while retaining its energy. Therefore the dynamics of self-focusing and self-compression of laser beam in plasma have been studied both theoretically and experimentally by many investigators extensively since long and have been reported in a number of investigations.[11–16] The effect of self-compression mechanism on the self-focusing of a Gaussian laser beam in an unmagnetized plasma has already been investigated by Bokaei and Niknam.[17] They have shown in their work that in the presence of ponderomotive nonlinearity the self-focusing mechanism is obstructed by the self-compression one. Shibu et al.[14] have investigated the self-compression of Gaussian laser beam due to the relativistic mass nonlinearity and have observed that the self-focusing mechanism interferes strongly with the non-linear self-compression process. Recently Bokaei et al.[18] have studied the effect of external magnetic field and plasma inhomogeneity on simultaneous self-focusing and self-compression of a Gaussian laser beam through the plasma. Their results showed that the simultaneous use of both external magnetic field and density ramp leads to generate highly focused and compressed pulses.
Most of the theoretical study on self-focusing and self-compression is devoted to cylindrically symmetric Gaussian laser beams.[19–20] Few studies of self-focusing have been reported on elliptical Gaussian beam,[21–23] cosh Gaussian beams,[24] Hermite Gaussian beams,[25] Hermite-Cosh-Gaussian beams[26] and super Gaussian beams.[27] From our studies, we have observed that, presently, there is an increase in interest in exploring a new technique of combining multiple beams to achieve high power densities at the target.[28–31] However combining identical four beams is mathematically simpler than combining two beams. This is because the intensity distribution of the beam formed by combining four identical beams is symmetrical in x- and y-directions, hence only one beam width parameter is required to describe the whole beam dynamics.
In the present investigation, we have focused on the self-focusing of a quadruple Gaussian laser beam comprising four coherent Gaussian laser beams propagating along the z-direction, but having intensity maxima in the x-y plane at (−xo,0), (xo,0), (0,−xo), (0,xo), in a collisionless magnetized plasma. However, in most plasma fusion experiments, the externally applied or self generated magnetic fields play an important role in laser beam propagation.[32–33] Therefore, it is justified to investigate the propagation of the quadruple Gaussian laser beam through plasma in the presence of a static magnetic field. The self-focusing mechanism in the presence of self-compression mechanism will be analyzed in contrast to the case in the absence of it. On a short time scale (t < τe) where τe is the energy relaxation time in a collisionless plasma, the nonlinearity due to ponderomotive force is dominant. This ponderomotive force of the laser causes perturbations in the electron density of plasma, which consequently leads to more refractive index gradient. Therefore, the electron density perturbation due to ponderomotive force is the main source of nonlinearity which modifies the plasma refractive index and makes it intensity dependent. The longitudinal refractive index gradient causes self-compression and transverse refractive index gradient leads to self-focusing of a laser beam. When the magnetic field is applied along the direction of propagation of beam, there are two modes of propagation, namely extraordinary and ordinary mode. Therefore, the redistribution of carrier is affected by the change in the strength of the static magnetic field. In weak coupling limit, we can consider the propagation to be in either of the two modes. In Sec.
Consider the propagation of a linearly polarized quadruple Gaussian laser beam of angular frequency ωo along the z-direction in a collisionless magnetoplasma. The external magnetic field Bo is applied along the direction of propagation of wave. In linear approximation, the propagation of laser beam can be assumed in either of the two modes of propagation namely ordinary and extraordinary. The electric field vector of the laser beam may be expressed as
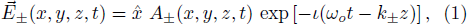
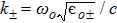
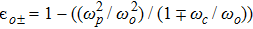
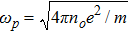
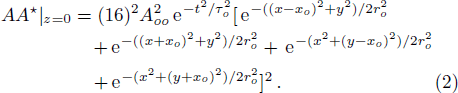
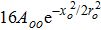
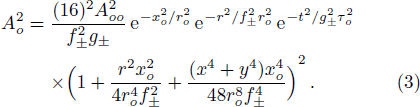
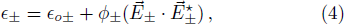
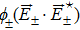
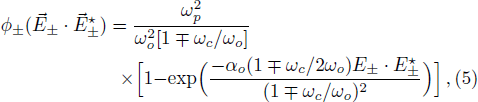
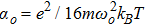
The nonlinear wave equation governing the evolution of the electric field in magnetoplasma is
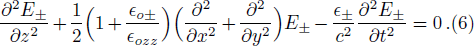
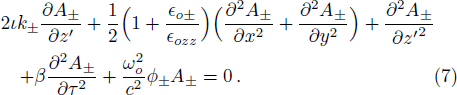
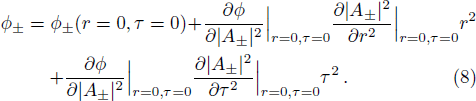
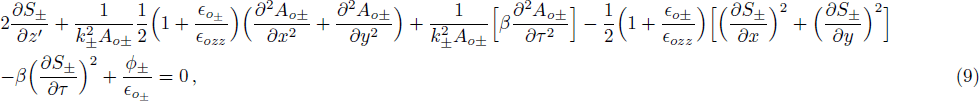
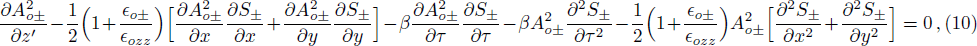
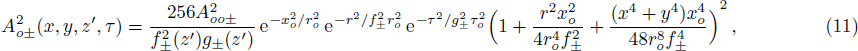
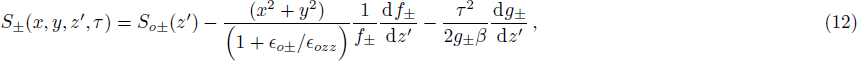
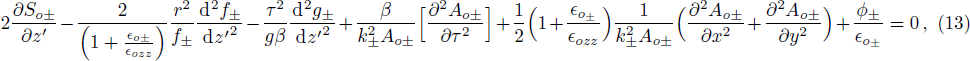
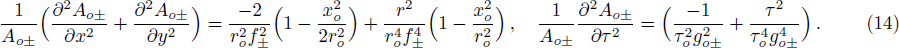
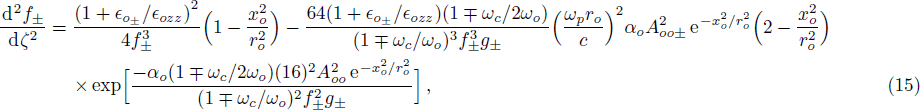
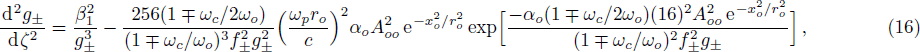
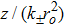
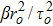
The initial condition d2f±/dζ2 = 0, for a plane wave front at ζ = 0, f± = 1, df±/dζ = 0, and g± = 1, dg±/dζ = 0 leads to the propagation of the quadruple Gaussian beam in the uniform waveguide/self trapped mode. By putting d2f±/dζ2 = 0, in Eq. (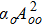
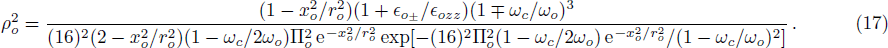
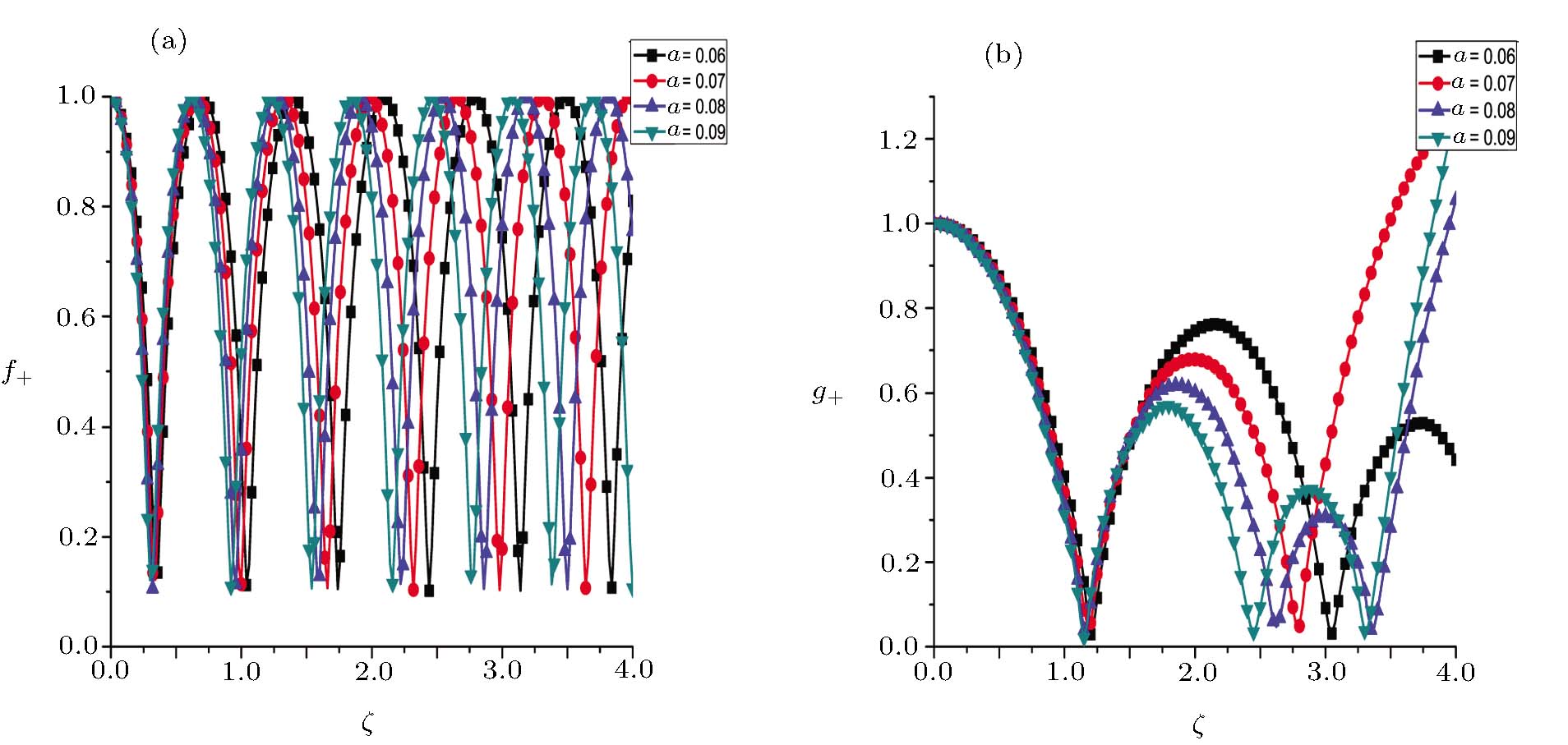
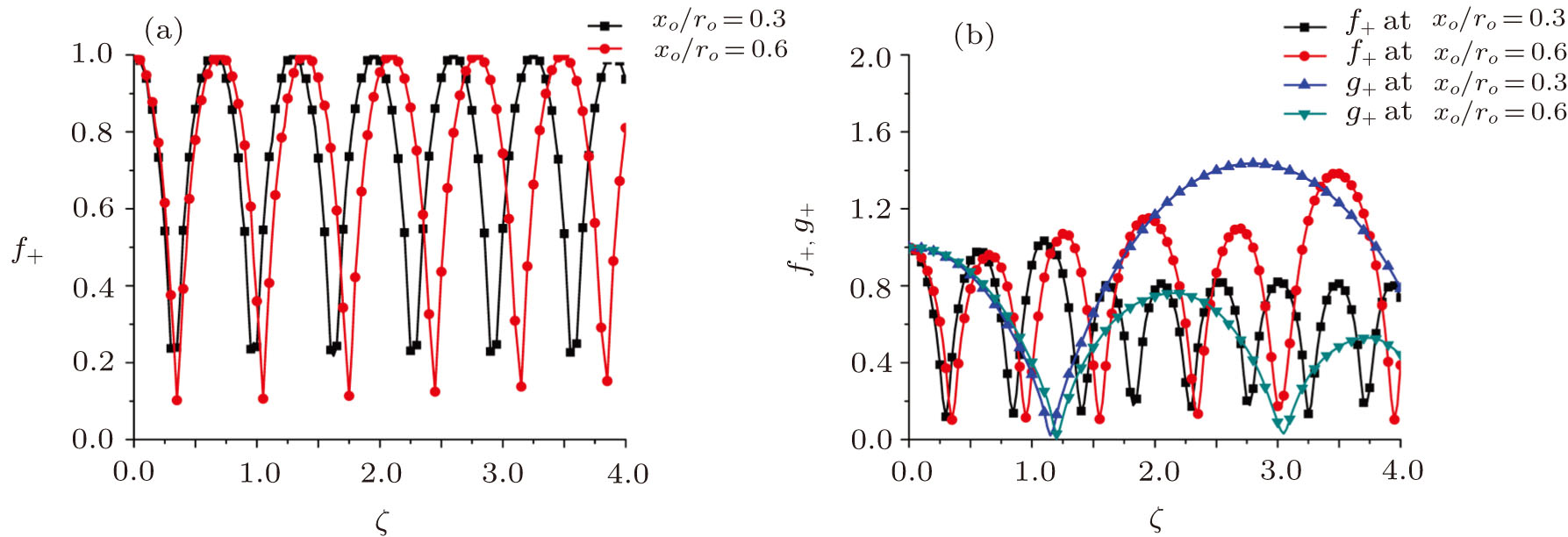
It is observed from Fig. 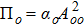
Equations (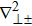
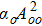
Figures 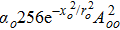
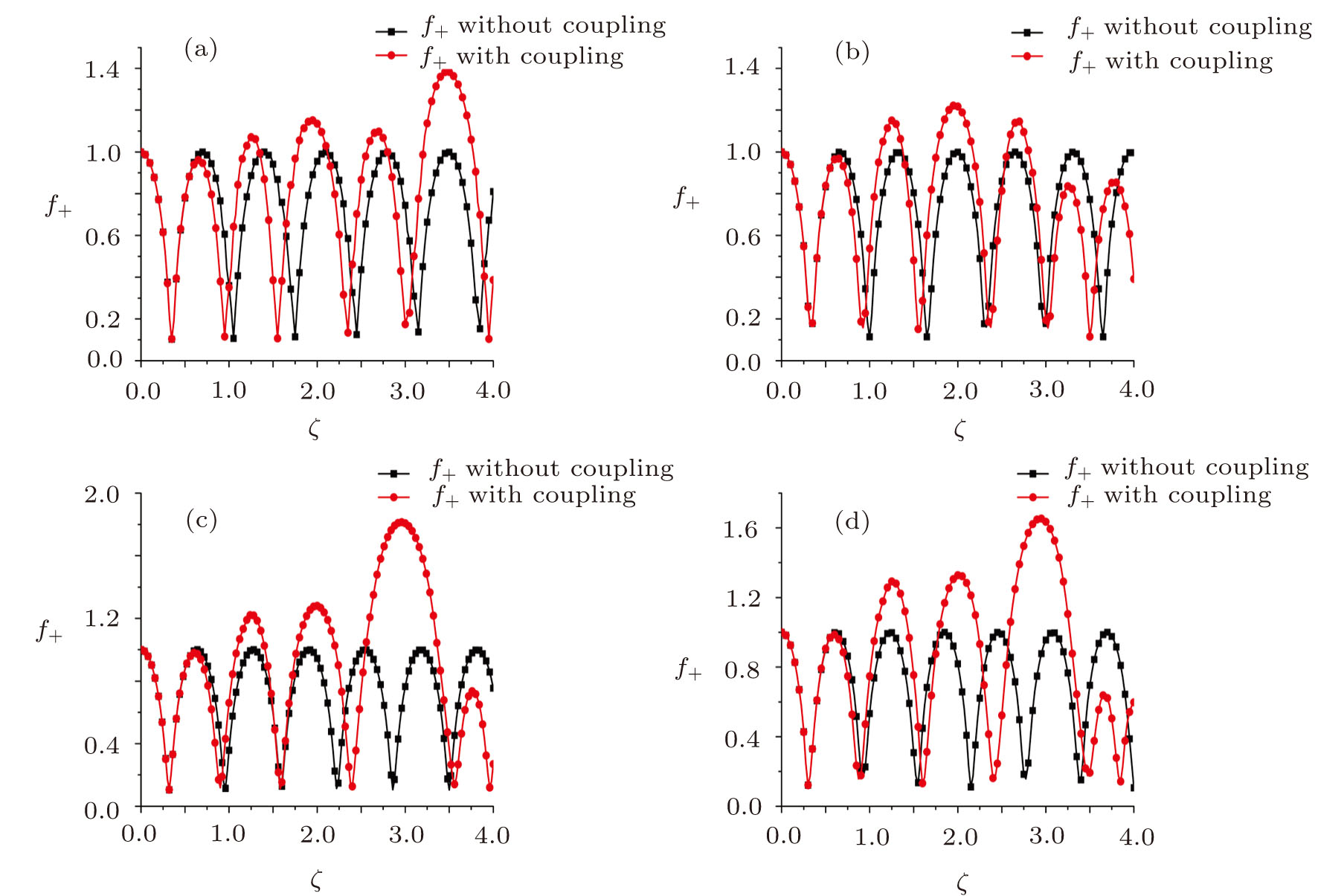
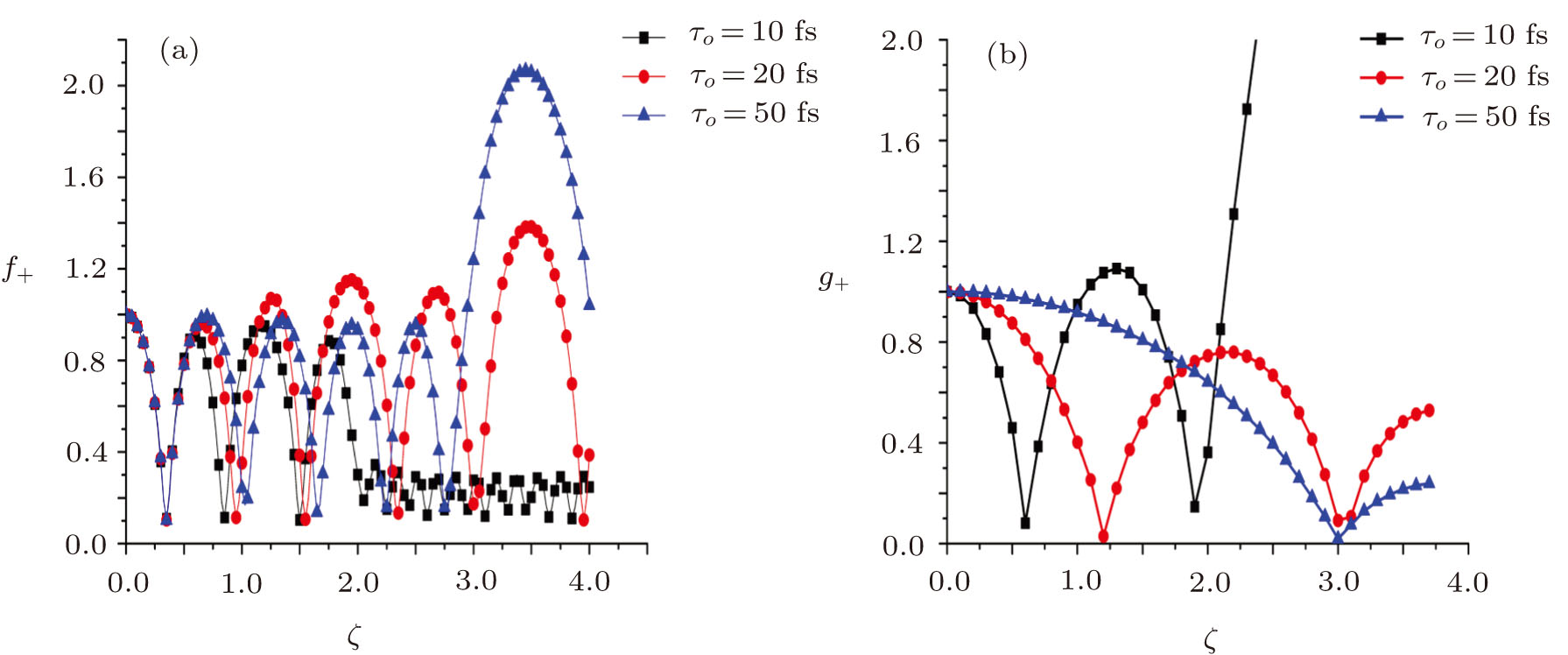
The effect of ponderomotive nonlinearity on simultaneous focusing and compression of the pulse is presented in Fig.
The same trend is observed for a = 0.08. But as the intensity parameter reaches to 0.09, the self-compression mechanism completely obstructs the pulse self-focusing. The physical mechanism behind this phenomenon can be explained as follows: by increasing the initial laser intensity, the ponderomotive force increases and pushes the electrons outward from the central region of the beam. Therefore, after a certain laser intensity value (lower-limit intensity), the refractive index gradient, produced via ponderomotive force becomes strong enough to focus the beam. By further increasing the initial laser intensity, the ponderomotive force becomes stronger and causes the complete expulsion of plasma electrons. As a result, the electron free channel is created in a certain region, which is responsible for defocusing of the laser beam. Hence, after a certain laser intensity threshold (upper-limit), the beam starts to defocus.[37] By compressing the laser pulse, the laser intensity goes up and reaches the upper-limit, as a result the beam diverges.
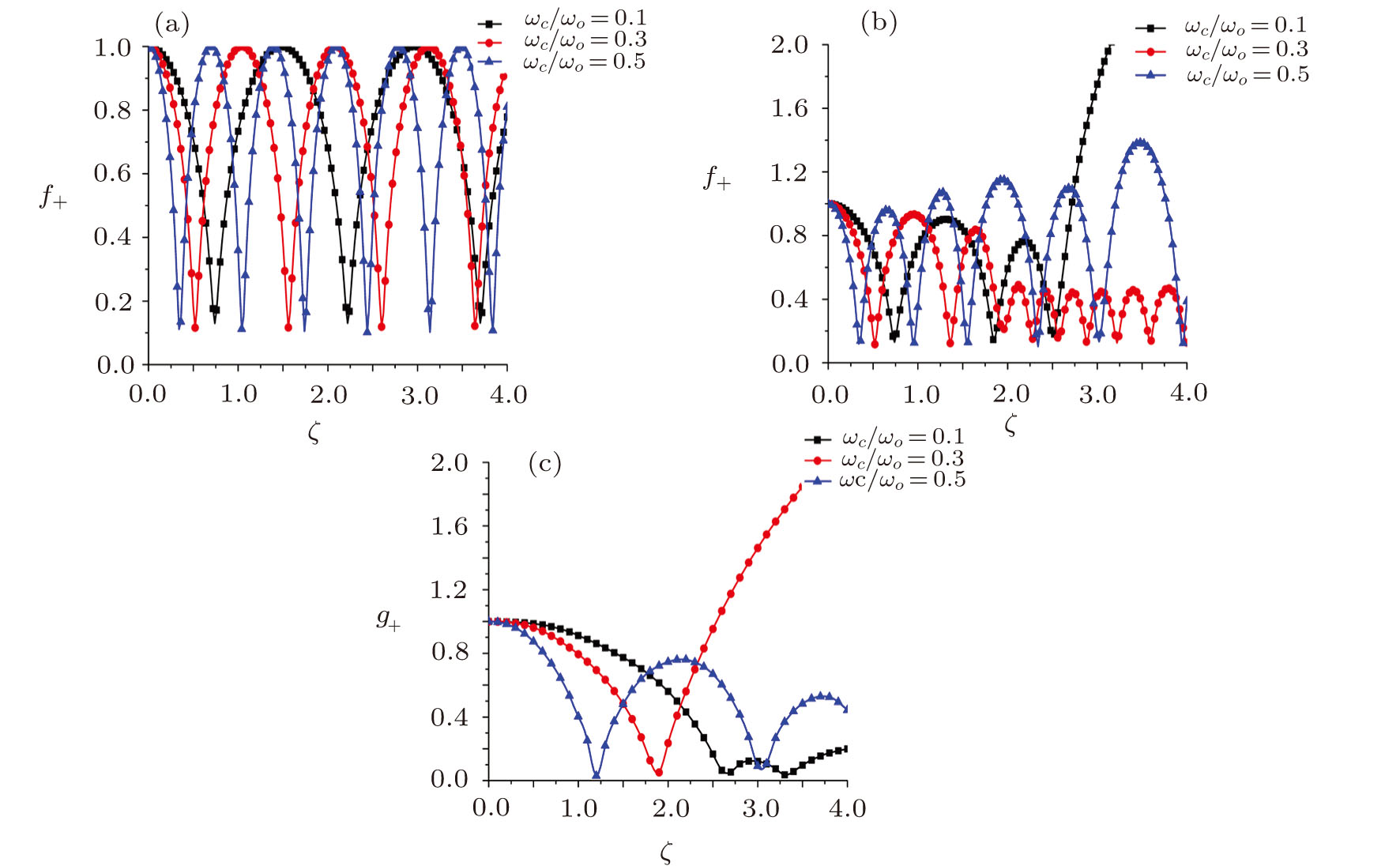
However, Fig.
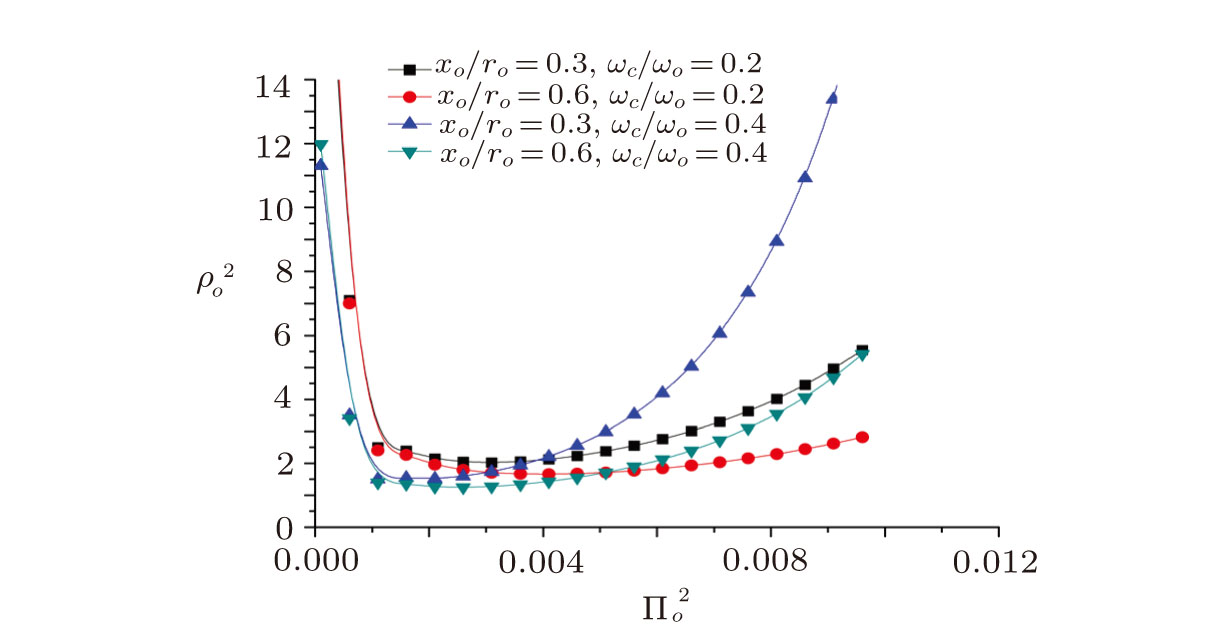
The effect of lateral separation of the beam component is studied in Fig.
Comparison of Fig.
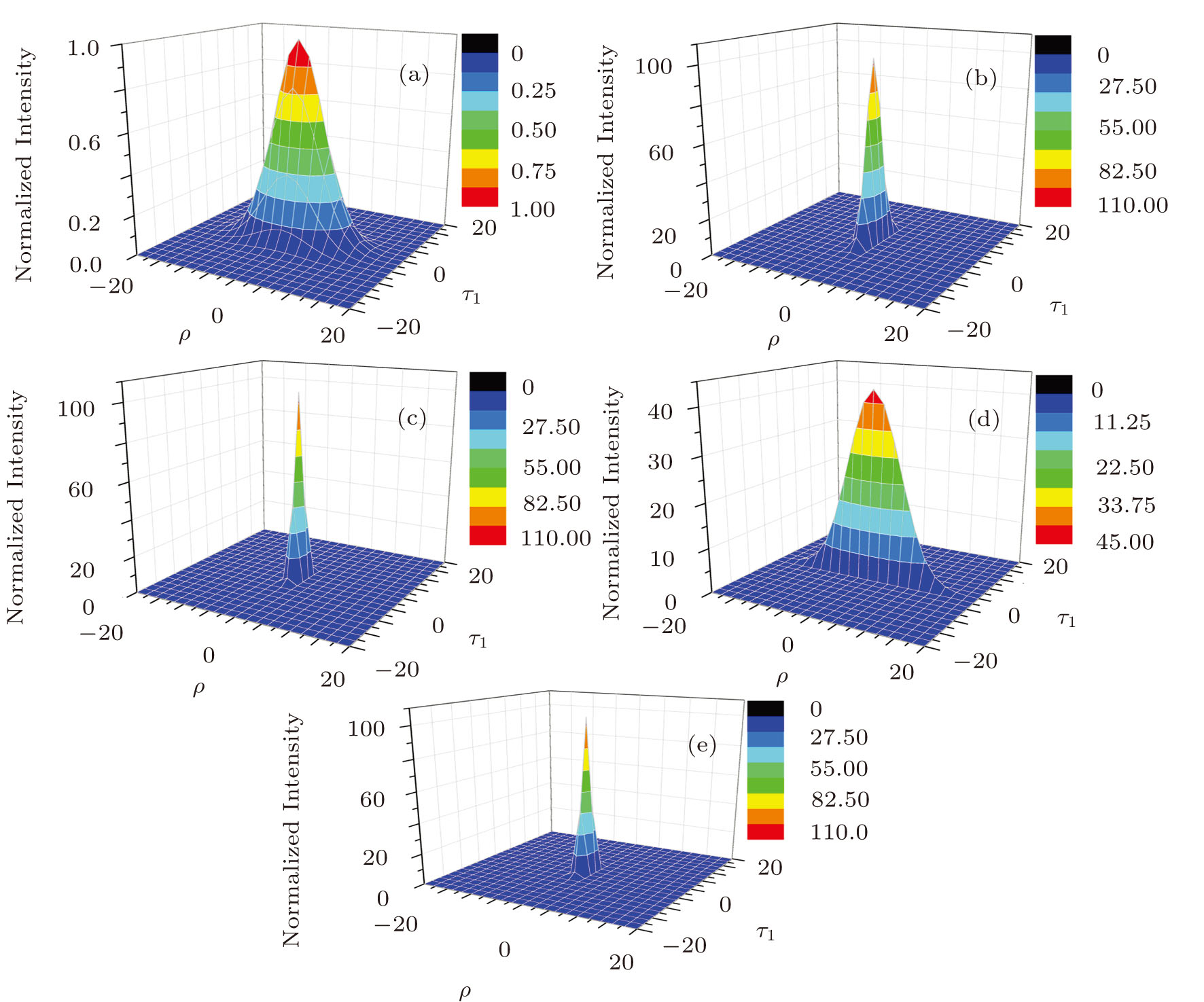
Figure 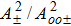
In the last, Fig.
We have studied the propagation of a quadruple Gaussian laser beam in collisionless magnetized plasma with two normal modes of propagation i.e. extraordinary and ordinary mode. Variation of beam width parameter with normalized distance of propagation has been evaluated and numerically simulated over wide range of initial intensity, magnetic field and lateral separation parameter. The self-focusing mechanism is studied in the presence of self-compression mechanism. It can be observed that, in case of ponderomotive nonlinearity, the pulse self-focusing is obstructed by the self-compression mechanism. From numerical simulation, it is found that the magnetic field is found to have a profound effect on the overall propagation laser beam through plasma and explicit enhancement in self-focusing of extraordinary mode. In the last, we also have plotted the 3-D graphs showing spatiotemporal evolution of a quadruple Gaussian laser pulses in magnetized plasma. Regarding applications, the results of the present investigation may be relevant to the applications where multi-beam mega joule laser is required, especially in laser induced fusion, which further helps in various applications of space like laser propulsion, laser energy network in space, energy supply to the ground energy system etc.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] |