Cite this Article
Tang Hao, Sun Cheng-Yi, Wu Bin, Song Yu, Yue Rui-Hong. Self-consistency of a Modification Method Based on Membrane Model with Minimal Length Considered. Communications in Theoretical Physics, 2018, 70(3): 299  
Permissions
Self-consistency of a Modification Method Based on Membrane Model with Minimal Length Considered
Tang Hao1, 2, 4, Sun Cheng-Yi2, 4, Wu Bin2, 3, 4, †, Song Yu2, 4, Yue Rui-Hong2, 5
School of Science, Xijing University, Xi’an 710123, China
Institute of Modern Physics, Northwest University, Xi’an 710069, China
School of Physics, Northwest University, Xi’an 710069, China
Shaanxi Key Laboratory for Theoretical Physics Frontiers, Northwest University, Xi’an 710069, China
College of Physical and Technology, Yangzhou University, Yangzhou 225009, China

 

† Corresponding author. E-mail: binwu@nwu.edu.cn

Supported by the National Natural Science Foundation of China under Grant Nos. 11675139, 11605137, 11435006, 11405130, the Double First-Class University Construction Project of Northwest University, the China Postdoctoral Science Foundation under Grant No. 2017M623219, and Shaanxi Postdoctoral Science Foundation

Abstract
Abstract

By adopting a result from generalized uncertainty principles (GUP), we modify the inner bound of the membrane model to a physical fixed value and get the cut-offs naturally rather than by hand, which are both in brick-wall model and membrane model, and the semi-classical quantization condition could always be valid as well. We also calculate the entropies of Schwarzschild-de Sitter black hole and find the GUP we choose qualitatively shows that the requirement of mass in this method is the same as the natural requirement of the Schwarzschild-de Sitter black hole, which means the method might be self-consistent.

Keyword:entropy;black hole;generalized uncertainty principle;brick-wall model;membrane model
1 Introduction

Bekenstein[1] and Hawking[2] proposed that a black hole should have entropy, and showed that the entropy of a black hole is related to its area of the event horizon. Explicitly, the relation is S = A/4, where S is the entropy, and A is the area of the black hole’s event horizon. This is called the Bekenstein-Hawking entropy. After that, the entropy of black holes have been studied for decades. People have developed many methods to calculate the entropy of black holes. The results mainly support the idea that the entropy of a black hole is directly proportional to it’s area of the event horizon. One of these called the brick-wall model[3] is widely used, which is brought out by G’t Hooft on 1985. This model believes that the entropy of a black hole is the entropy of the quantum gas in thermal equilibrium exists between the external fields and the black hole horizon in a spatial region, which is called the “brick-wall”. With this method, people have obtained many useful results.[4–10] This model gives us a clearer and easier method for calculating the entropy of a black hole and gives acceptable explanations. Normally, the formulation of the entropy contains many parts. One of the parts contributes the main entropy component while others are just small corrections.

Liu and Zhao[11] modified this model. They believe that the main part of the entropy may come from a very thin wall named the membrane[12–13] (or called the film[14]), which is called the membrane model. This model is more simple, some papers had studied the entropy with this model[12–16] and got some beautiful results. Mathematically, this model assumed that the thickness of the wall could reduce to zero. Thus, the entropy of a black hole could be taken as the entropy of a two-dimensional membrane. This view is very charming, and could give a nice result. But, physically, if the thickness of the wall reduces to zero, the semi-classical quantization, which is used in the membrane model might be invalid.

However, both the brick-wall model and the membrane model contain the disadvantages that there need a cut-off taken by hand in order to satisfy the result of the Bekenstein-Hawking entropy. Moreover, the physical picture is not quite clear.

To solve this puzzle, we modify the membrane model. Since the thickness of the wall should not reduce to zero, we could change the lower limit to a finite value. This value should have its own physical meaning. If we change this limitation, the calculation of the entropy will be a little different. The Planck unit ħ = c = G = 1 has been taken throughout this paper.

2 The Modification Method

For a Schwarzschild black hole, the line element reads

where M is the mass of the black hole. Put it into Klein-Gordon equation for scalar field

where g = −r4 sin2θ is the determinant of the metric. Then one can get

Decompose the wave function into the form of

and substitute into Eq. (3), then one could get

Use Wentzel-Kramers-Brillouin (WKB) approximation, let

put it into Eq. (5), and define a radial wave number k(r,l,ω) by

After takeing the semi-classical quantization condition, the number of radial modes n in membrane model is

where ϵ is the distance between event horizon and the inner membrane surface, δ is the thickness of the membrane.

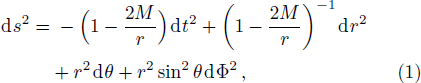
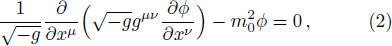
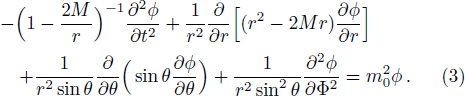
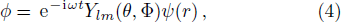
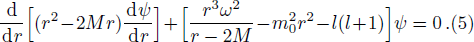
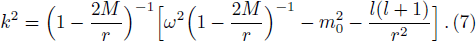
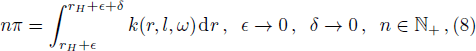
The cut-off is related with parameters ϵ and δ in membrane model, which is chosen by hand, and the physical meaning of the choice is also not very clear. Besides, when ϵ → 0, the semi-classical condition might be invalid near the Planck scale. We would like to discuss and reconsider the parameter ϵ.

It is generally believed that the Planck scale exists in our universe[1,17–19] and several theories based on this got some good results. Moreover, the loop quantum gravity theory found the evidence that the space is Planck scale discrete[20] in nature. It announced that the area and volume have discrete spectrum.[21–22]

Besides, many efforts have been devoted to the GUP recently. The simplest formulation of generalize the uncertainty relation reads[23]

where ħ is the Planck constant, Δx and Δp are the spatial coordinates and momenta respectively, λ is of order of the Planck length. It shows that there exists a minimal length as[24–28]

In Ref. [25], the authors also gave the proper distance vicinity near the horizon of order of the minimal length . Based on those pictures, they use the traditional way to recalculate the entropy of black holes by concerned of the GUP. In Ref. [25], we have

then one can get

where ϵ is the distance between the horizon and the corresponding inner surface of the “membrane” in membrane model.

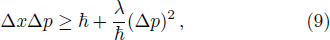
In Refs. [24--27], the authors calculated the entropy and gave the result in Eq. (11). This might bring us a way to modified the inner distance into a fixed value, which means that we do not need to assume ϵ to be a free number, which might be zero. The physical meaning of Eq. (11) is just the upper bound of the vicinity near the horizon.[24–25] Now that the upper bound has been set, and the membrane is outside the horizon, we now set ϵ into 2λκ. Then we can see that the inner distance ϵ is corresponding to the surface gravity κ of the black hole now. Thus, the value of ϵ stands for a indigenous property of a black hole, which is connected with the black hole.

If we set ϵ = 2λκ, Eq. (8) could be rewritten as

Since the scaler field is regarded as pure energy, i.e. as photons, the chemical potential of the photons in thermal equilibrium should be zero. Then the free energy is

The m0 in the latter integral in Eq. (14) will be vanished when r → 2M. Then one could get the free energy as

The entropy is

If the cut-off is taken as

then, the entropy becomes

One could get δ from Eq. (17) as

Since κ = 1/4M, β = 1/T = 8πM, where T is the temperature of the black hole. Equation (19) could be written as

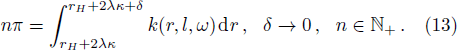
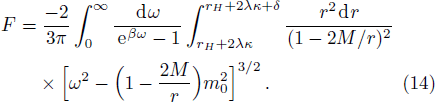
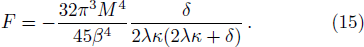
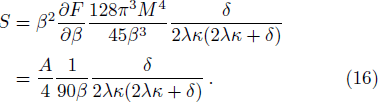
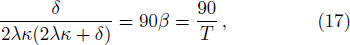
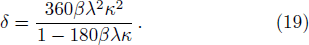
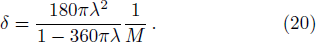
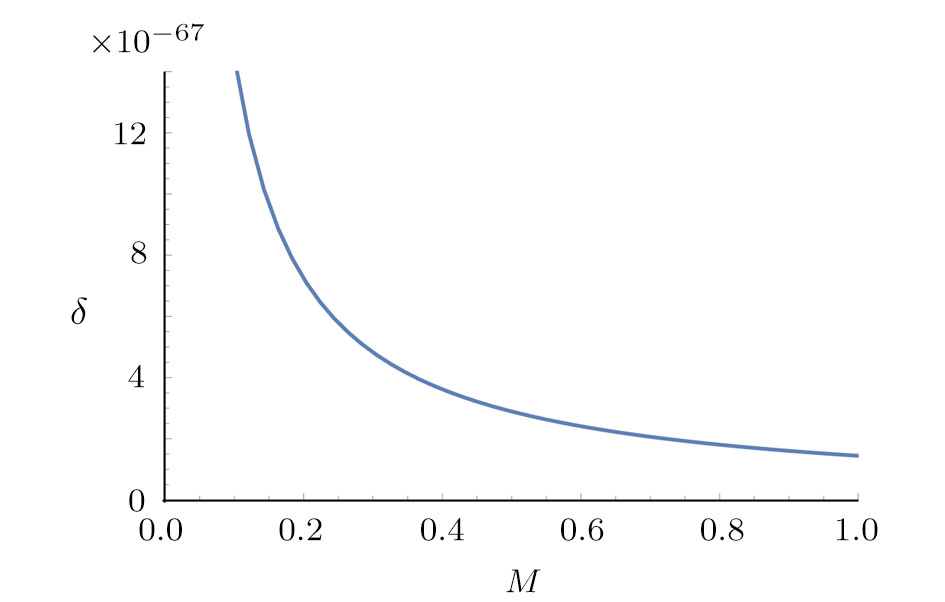
By using this method, we also get the Bekenstein-Hawking entropy of a black hole. From Eq. (20), we can see that δ is just related to the mass of the black hole itself. The bigger the mass, the thinner the membrane. Since the mass of the black hole could not be infinite, the value of δ could not be zero physically. Then, the standing-wave conditions (13) would always be valid.

In order to see whether the parameter δ is really small enough to form a membrane or not, we could discuss the relationship qualitatively by roughly setting λ = lp = 10−35. Then Eq. (20) becomes into

and we could get the plot of δ–M in Fig. 1. We could see that the value of δ is very small, which means the membrane is very thin. This decreasing curve implies that the larger the mass, the thinner the membrane. Since the mass of the black hole could not be infinite, the parameter δ would always be positive. The GUP we chose make the semi-classical quantization condition in Eq. (13) always be valid.

Fig. 1 Plot of δ with M of Schwarzschild black hole.

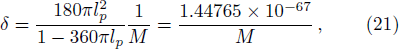
It seems there is nothing special for this modification, the semi-classical quantization may not be quite important. However, when use this modified method to calculate the entropies of Schwarzschild-de Sitter black hole, we find something interesting.

3 The Self-consistency

For a four-dimensional Schwarzschild-de Sitter black hole, the line element is[29]

with

where M is the mass of the black hole, Λ is the cosmological constant. The three horizons are[30]

where . The r− has no physical meaning, rH is the event horizon, and rC is the cosmological horizon. For simplicity, we just take the rH to demonstrate, since it is easy to prove that the result of rC is similar with rH.

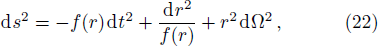
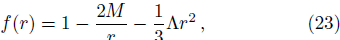
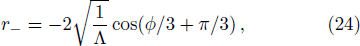
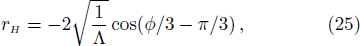
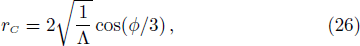
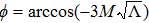
The surface gravity of rH is[30]

and the corresponding temperature of rH is[30]

By using the similar calculations with the Schwarzschild black hole in Sec. 2, one could gets

where δH is the thickness of the membrane. If the cut-off is as

one could get

where is the area of the event horizon at rH. Then,

Substituting Eqs. (27) and (28) into Eq. (32) and also discussing the relationship qualitatively by roughly setting λ = lp = 10−35 and Λ = 1, one could get the plot of δ-M in Fig. 2.

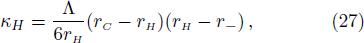
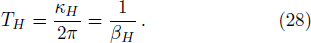
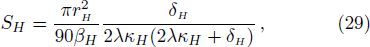
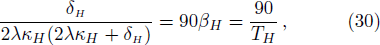
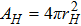
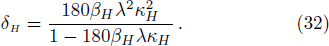
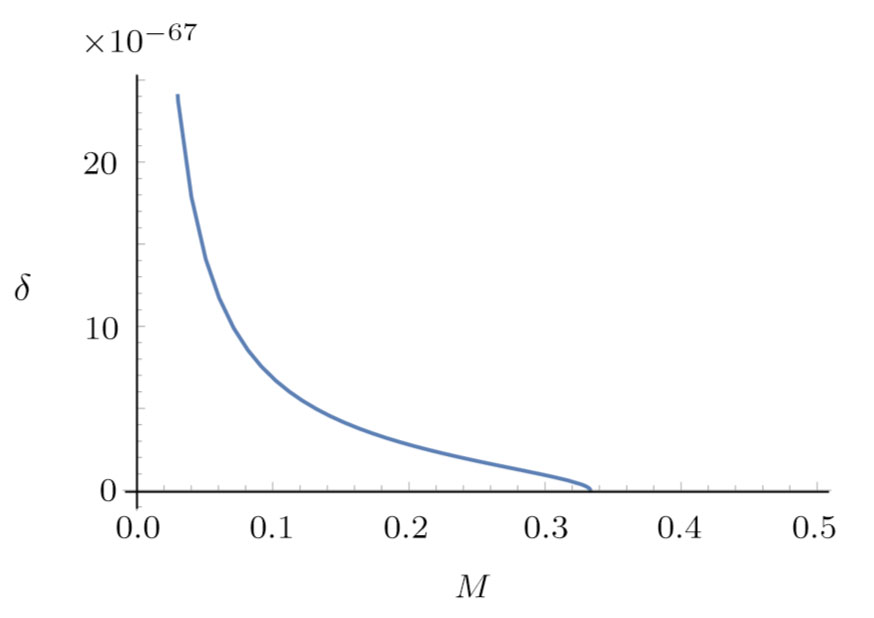Fig. 2 Plot of δH with 0 < M < 0.5 of a Schwarzschild-de Sitter black hole, M is not chosen in a good range. The parameter δH = 0 at M = 1/3.

From Fig. 2 we can see that the thickness of the membrane δH is also inversely proportional to the mass M. But we also see that δH could be zero in Fig. 2. Does this mean that the requirement of δH > 0 is wrong?

To check this, we solve δH=0 from Eq. (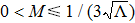32) with Λ=1, λ = lp, then we get M = 1/3. For a Schwarzschild-de Sitter black hole, it is required that rC > rH. From Eq. (23), we require that . If Λ = 1, then we have 0 < M ≤ 1/3. M = 1/3 stands for an extremal Schwarzschild-de Sitter black hole, which is not allowed in our calculation. This means that the requirement of δH > 0 also reflect the natural requirement of Schwarzschild-de Sitter black hole. The natural choice of cut-off in Eq. (32) might be self-consistent. Since δH > 0, the semi-classical quantization condition is always valid as well.

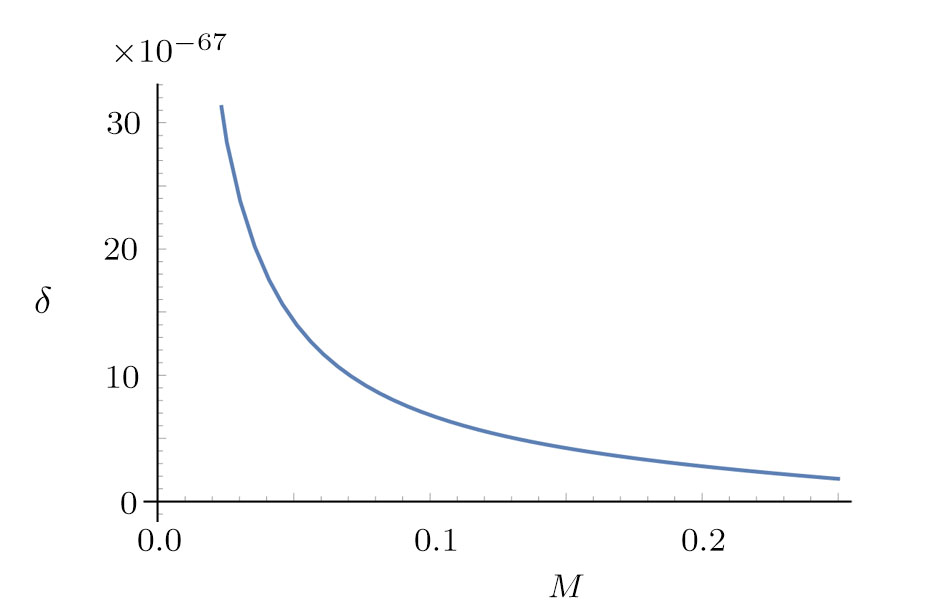Then, by choosing the proper range of M, we could get Fig. 3, which is similar with Fig. 1. The order of the magnitudes in Fig. 3 is also close to the order of the magnitudes in Fig. 1. Both of the results show that the parameter δ is very small and just related to the mass M.

Fig. 3 Plot of δH with 0 < M < 0.25 of a Schwarzschild-de Sitter black hole, M is chosen in a proper range. The parameter δH is always positive.

For a Schwarzschild-de Sitter black hole, we could also get the entropy by natural cut-off, which is determined by its mass. Moreover, one could see that the GUP we used might be self-consistent by calculating the entropy of a Schwarzschild-de Sitter black hole, which might reflect the natural of the Planck scale.

4 Summary

In summary, by using the results and ideas from the generalized uncertainty principle, we have modified the inner bound of the membrane model and got the Bekenstein-Hawking entropies with cut-offs, which were chose by nature rather than by hand. We have also uncovered a result that the thickness of the membrane is only connected with the mass of the black hole itself. The inner distance ϵ is a fixed value, which is determined by the black hole itself with κ as well. Besides, the semi-classical quantization condition could be always valid since the parameter δ is always positive. Since the inner bound is set to a fixed value, we find the requirement of δ also reflects the natural requirement of a Schwarzschild-de Sitter black hole, which means that the GUP we choose is self-consistent and this modification might reflect the physical meaning of the Plank scale. We would like to check this result in other kind of black holes in the future works.

Reference
[1] Bekenstein J. D. Phys. Rev. D 7 1973 2333
[2] Hawking S. Commun. Math. Phys. 43 1975 199
[3] Hooft G’t Nucl. Phys. B 256 1985 727
[4] Won T. K. Phys. Rev. D 59 1999 047503
[5] Liu W. B. Chin. Phys. Lett. 20 2003 440
[6] Masakatsu K. Kamal K. N. Kazuyasu S. Class. Quantum Grav. 22 2005 3923
[7] Ghosh K. Nucl. Phys. B 814 2009 212
[8] Latham T. Gershon T. arXiv: 0809.0872v1 [hep-ph] 2008
[9] Wontae K. Edwin J. S. Myungseok Y. arXiv: 0808.1805v1 [gr-qc] 2008
[10] Lee C. O. arXiv: 1402.3972v2 [gr-qc].
[11] Li X. Zhao Z. Chin. Phys. Lett. 18 2001 463
[12] Gao C. J. Shen Y. G. Chin. Phys. Lett. 18 2001 1167
[13] Li X. Zhao Z. Int. J. Theor. Phys. 40 2001 903
[14] Liu W. B. Zhao Z. Chin. Phys. Lett. 18 2001 310
[15] Li X. Zhao Z. Phys. Rev. D 62 2000 104001
[16] Li X. Zhao Z. Chin. Phys. Lett. 23 2006 2016
[17] Garay L. J. Int. J. Mod. Phys. A 10 1995 145
[18] Doplicher S. Fredenhagen K. Roberts J. E. Commun. Math. Phys. 172 1995 187
[19] Kiefer C. Gen. Rel. Grav. 41 2009 877
[20] Rovelli C. Living Rev. Relativity 11 2008 5
[21] Rovelli C. arXiv: 1012.4707v5 [gr-qc] 2012
[22] Ashtekar A. Baez J. Corichi A. et al. arXiv: 9710007v1 [gr-qc] 1997
[23] Park M. arXiv: 0709.2307v4 [hep-th] 2007
[24] Tang H. Sun C. Y. Yue R. H. Commun. Theor. Phys. 68 2017 64
[25] Li X. Phys. Lett. B 540 2002 9
[26] Garay L. J. Int. J. Mod. Phys. A 10 1995 145
[27] Kempf A. Mangano G. Mann R. B. Phys. Rev. D 52 1995 1108
[28] Chang L. N. Minic D. Okamura N. et al. Phys. Rev. D 65 2002 125028
[29] Eune M. Kim W. Phys. Lett. B 723 2013 177
[30] Liu W. B. Zhao Z. Acta Math. Sci. 23 2003 69