† Corresponding author. E-mail:
Supported by the National Natural Science Foundation of China under Grant Nos. 11574041, 11475037, and 11704026
We develop a master equation approach to describe the dynamics of distant resonators coupled through a one-dimensional waveguide. Our method takes into account the back-actions of the reservoirs, and enables us to calculate the exact dynamics of the complete system at all times. We show that such system can cause nonexponential and long-lived photon decay due to the existence of a relaxation effect. The physical origin of non-Markovianity in our model system is the finite propagation speed resulting in time delays in communication between the nodes, and strong decay rate of the emitters into the waveguide. When the distance satisfies the standing wave condition, we find that when the time delay is increased, the dark modes formation is no longer perfect, and the average photon number of dark mode decreases in steady time limit.
Quantum network is the backbone of distributed quantum computing architecture and quantum commu-nication.[1–2] It comprises of a set of nodes exchanging quantum information via connecting quantum channels. Quantum networks include both local quantum networks connecting small-scale quantum computers,[3–5] or wide-area quantum networks between distant nodes.[6] The former mainly focuses on the local interaction between qubits, input-output formalism for few-photon transport[7–8] and the local quantum information process such as single-photon router,[9–11] quantum rectifier,[12–14] and quantum gates.[15–17] Due to high propagation speed and small system scale, these works are mostly described by the Born-Markov (BM) approximation based on weak-coupling perturbation theory and the neglect of time delays in interactions.[18] Many local quantum network setups have been experimentally demonstrated in recent years.[19–20]
At the same time that the technology evolves, recent experiments begin to investigate the regime of a non-negligible delay time because of interest in scalable quantum networks.[21–24] Unlike local quantum network, a wide-area quantum network usually contains many distant nodes to implement long-distance quantum information tasks such as quantum state transfer between remote nodes.[1,25–26] The finite propagation speed of these excitations naturally introduces time delays in the dynamics, which can invalidate the Markov approximation. In order to analyze the non-Markovian effect of quantum network exactly, several analytical and numerical methods have been developed, where the Born-Markov approximation is not involved. This includes the numerical Green function approach,[27] the time-dependent Schrödinger equation approach,[28] the full quantum electrodynamical approach,[29] the path integral approach,[30] the extended master equation method,[31] and so on. However, an exact master equation describing the non-Markovian dynamics of a quantum network is rare. So, further development of theoretical methods is required.
In this paper, we study the non-Markovian dynamics of distant resonators coupled through a one-dimensional waveguide. The dissipation dynamics of the resonators alone are obtained by integrating out the degrees of freedom of reservoirs. As a result, the back-action between the waveguide and the resonators can be fully taken into account. We then derive the exact master equation non-perturbatively. The transient and steady state dynamics of the system can be obtained directly from the master equation. In the short time delay limit, we find that the exact solution given by our master equation is in good agreement with the Markovian solution in previous work, which justifies the validity of the Markov approximation. However, when the distance between the nodes is raised, the deviation between the exact solution and the Markovian solution can be extremely large. Under the standing wave condition, similar to the Markovian case, we find that the non-localized mode is uncoupled from the waveguide and become so-called dark mode of the system in the steady state limit. However, we notice that the average photon number in steady time limit decreases with the increase of time delay. Finally, by comparing with the exact numerical solution, we find that our master equation can accurately describe the non-Markovian dynamics of the system.
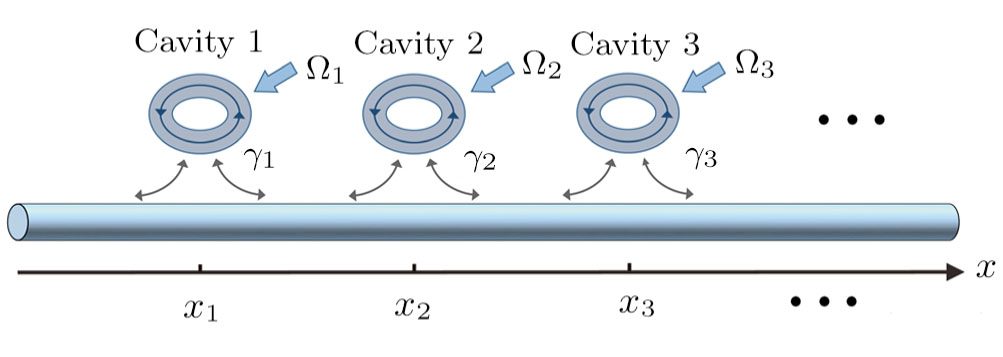
As illustrated in Fig.
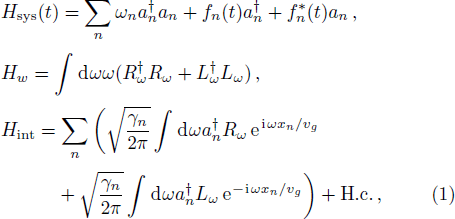
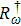
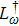
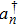
To investigate photon dynamics of distant cavities embedded in a one-dimensional waveguide, we shall concentrate on the reduced density matrix for the quantum emitter by tracing out the free degree of waveguide, ρ(t) = Trwρtot(t). We suppose that the waveguide is initially in the vacuum state and the initial density matrix is factorized into a direct product of the system and the waveguide state.[33] i.e., ρtot(t0) = ρ(t0) ⊗ ρw(t0). Using the Feynman-Vernon influence functional approach,[34–35] we can integrate out completely the waveguide degree of freedom in the coherent representation[36] and obtain the following exact master equation,
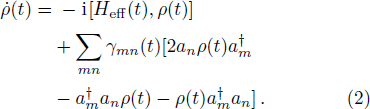
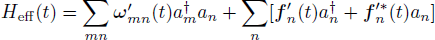
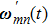
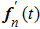
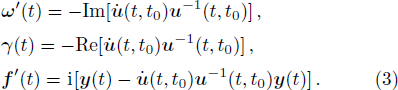
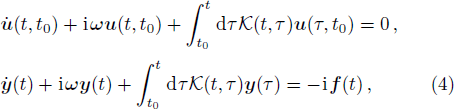
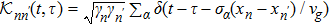
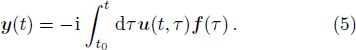
A quantum network consists in general of many nodes, which are connected by the waveguide to implement long-distance quantum communication via emission and absorption of photons. The finite propagation speed of photons naturally introduces time delays in the dynamics, which can invalidate the Markov approximation. To study Non-Markovian effects of retardation, first, we consider a minimal model of a pair of driven resonators coupled to the waveguide. For simplicity, we assume ω1 = ω2 = ω and γ1 = γ2 = γ. The large distance between two cavities is d = |x1 − x2|, such that the delay time td = d/vg between them is comparable to their lifetime, even greater than their lifetime. Using Eq. (
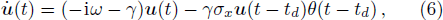
We note that Eq. (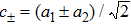
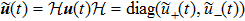
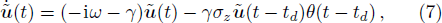
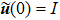
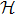
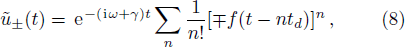
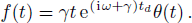
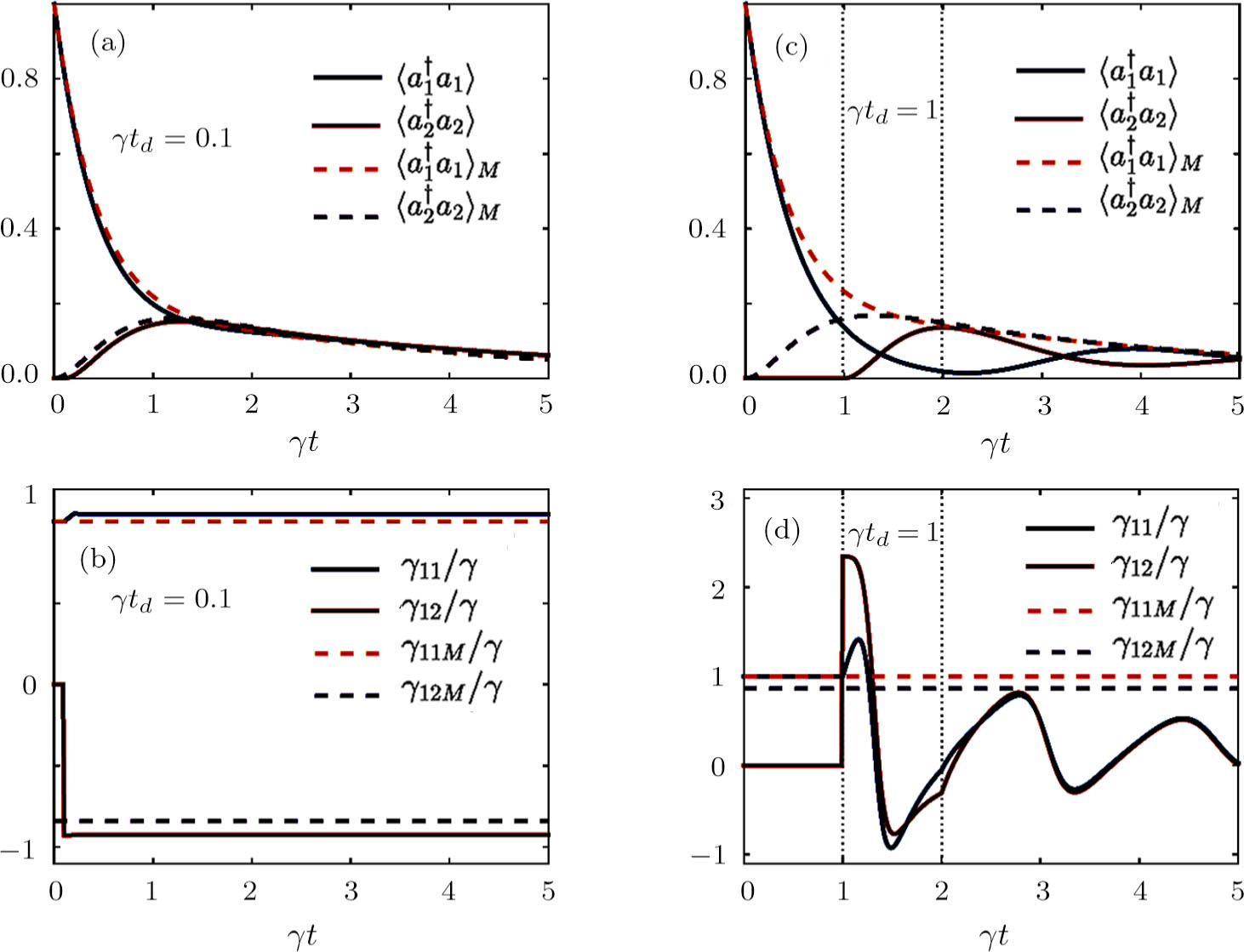
In this section, we study dissipation photon dynamics of distant resonators coupled to the waveguide beyond the Markovian regime. As discussed in the Introduction, Born-Markov approximation is valid when propagation time of the photon can be ignored, i.e. γtd ≪ 1. In this regime, Eq. (
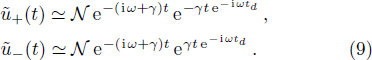
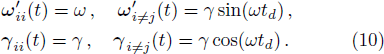
The photon dynamics of distant cavities, 
To study the regions of beyond the Markovian regime, we can increase the separation between the emitters. When the time delay td is comparable to the characteristic spontaneous emission time 1/γ, retardation effects play a significant role in the system dynamics and the Markovian master equation cannot describe system dynamics any more. Dissipation rate is not constant. The system dynamics depend on the time delay, and thus the time evolution of the system must be described by the exact master equation (
Figure
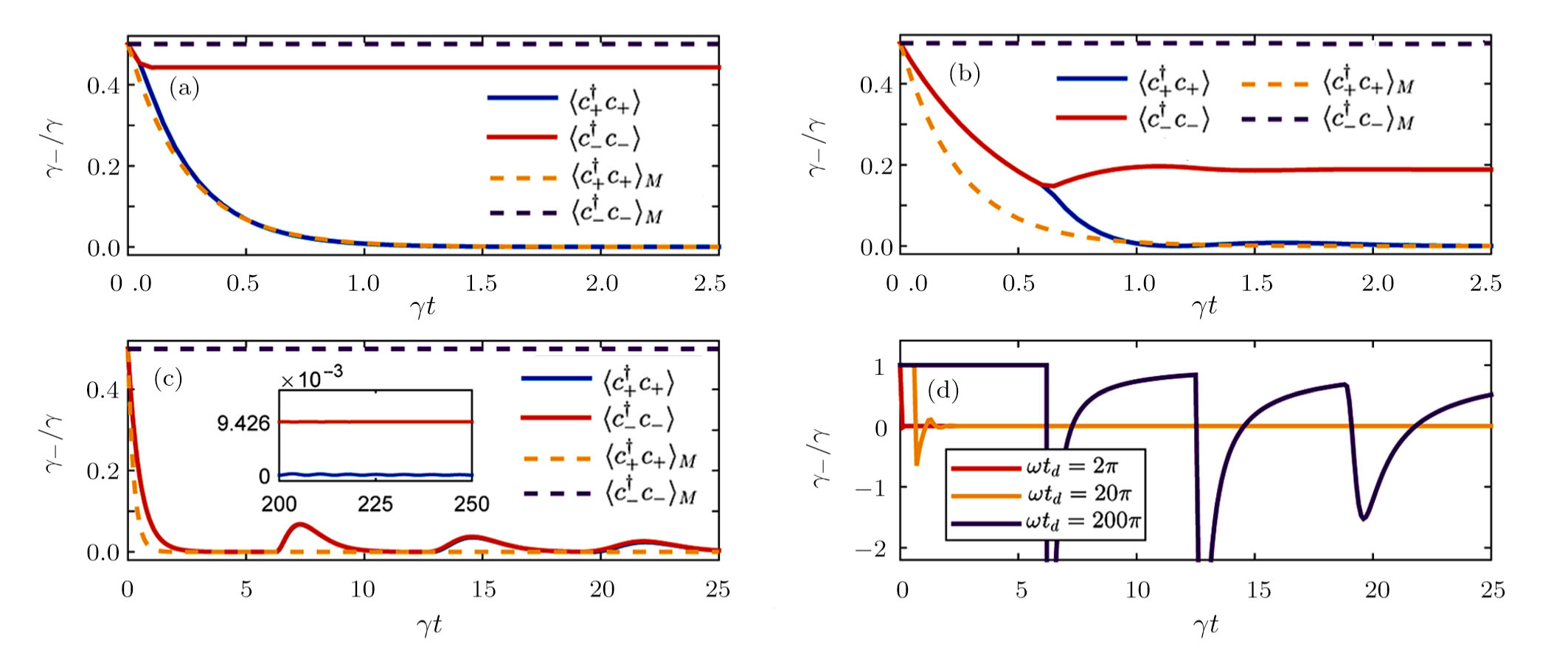
In the following, we discuss retardation effects in the long-time limit. From Eq. (
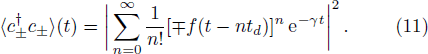
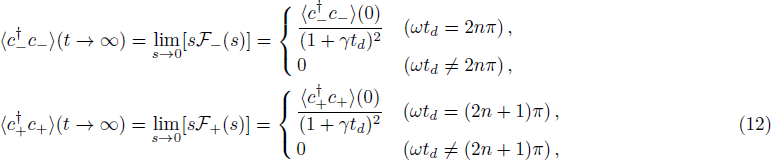
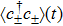
From Eq. (
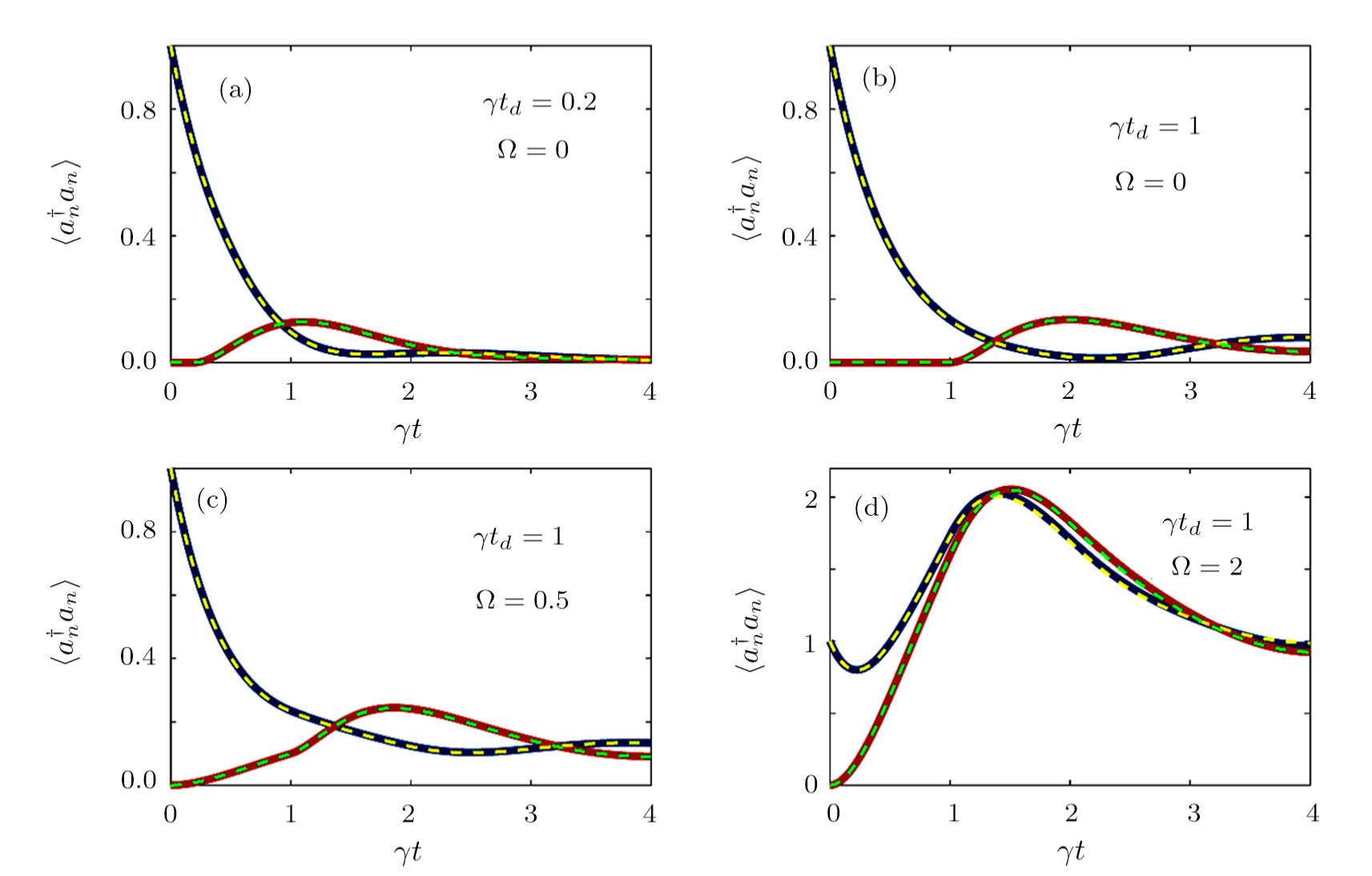
To give the regime of validity of our master equation method in this paper, we introduce matrix product states (MPSs) techniques,[46–47] which are originally developed in a condensed-matter context to enable an efficient description of one-dimensional many-body system. The state of the total system (cavities plus waveguide) is described as an MPSs and evolved according to the Schrödinger equation.[48] This allows one to simulate the non-Markovian dynamics of the system for large retardation time td. Figure
We have studied dissipation dynamics of distant resonators coupled through a one-dimensional waveguide. Making use of the Feynman-Vernon influence functional theory, we have derived an exact non-Markovian master equation for the distant resonators by treating the waveguide as environment. The back-reactions between waveguide and resonators are fully accounted. The photonic dynamics of the system can be obtained directly from the master equation. We have shown that the exact solution obtained from our master equation is in good agreement with the Markovian solution in previous work in the short time delay limit. Our results show that non-Markovian effects start to appear due to the increase of delay time. The deviations can be extremely large, and the Markov approximation is invalid in the long time delay regime. Similar to the Markovian situation, when the separation between the nodes is resonant for the symmetric (asymmetric) mode, the symmetric (asymmetric) mode is uncoupled to the waveguide and become so-called dark mode in the steady state limit. This is caused by a destructive interference between the different paths that the photon emitted by the two resonators. However, we have noticed that the average photon number in steady time limit decreases with the increase of time delay. Finally, we have verified the validity of our non-Markovian master equation by comparing the analytic solution derived from our master equation with the exact numerical solution obtained by the MPSs evolution method.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] |