Quantum systems usually interact with their surrounding environments, which leads to dissipation and decoherence since there is a flow of information between the system and the environment. Decoherence can be viewed as the loss of non-classical correlation of a system. Two widely used measures of non-classical correlation are entanglement and quantum discord. Entanglement, as a measure of quantum correlation without classical counterpart, has received much attention. It plays an important role in quantum information and communication theory,^[1–2] quantum teleportation,^[3] quantum cryptography,^[4–5] and universal computing.^[6–7] However, there is another non-classical correlation besides entanglement^[3–9] and it is very important in these fields. In order to distinguish all the non-classical correlation, Ollivier and Zurek took on a concept of quantum discord that can capture basic feathers of classical bipartite states. When the quantum discord is zero, the information is locally accessible and distant independent observers can gain it without disturbing these bipartite states. Though many scholars focus on the study of entanglement in last few years,^[10–14] the present work pays more attention to the study of quantum discord.^[15–16] It is more practical than entanglement to describing quantum correlation dynamics^[8,10] and is defined as the distinction between quantum and classical aspects of correlation in a composite quantum state. Entanglement and quantum discord behave very differently under certain reservoirs. In addition, the quantum discord can be employed to improve the efficiency of the quantum Carnot engine^[17] and to understand the quantum phase transition^[18] and the process of Grover search.^[19] It is believed that the quantum discord is more universal than entanglement, and is also investigated under a Markovian environment in recent literature for dissipative dynamics of a system.^[20] However, this character cannot be suitable for a non-Markovian environment.^[21–22]

The dynamical solution of a system interacting with a non-Markovian environment can also be employed in two projector operator technique, namely the Nakajima-Zwanzig (NZ)^[23–24] and time-convolutionless (TCL)^[25] master equations. The first one leads to an integral-differential evolution equation for the reduced density operator of a system, so that its time derivative depends on its history, whereas the second one leads to a generalized master equation local in time.^[26] Although the validity of the above two has been studied for the dynamics of atomic population and entanglement,^[27–28] we mainly study the effectiveness of non-Markovian master equations for the quantum discord dynamics of a system and discover some new phenomena.

In this paper, a general expression of the quantum discord for a subclass of the X structure density matrix is given. For a system of non-coupled two qubits, we can provide the exact solution under single excitation. What is more, the non-Markovian approaches can also be exploited to solve dynamics of this model. By means of the solution above, we mainly consider the validity on the dynamics of quantum discord in different regime of qubits independently coupled to their reservoir.

We first present a brief review of the concept for the quantum discord. After knowing the value of a random variable X in classical information theory, which takes values within a set of probabilities {p_x}, the information obtained can be quantified by its Shannon entropy^[1]H(x) = −Σ_x p_x log₂ p_x. For two such random variables X and Y, the correlation of them are measured by their classical mutual information. Extending the quantum field, quantum mutual information can be written as I(A:B) = S(ρ^A) + S(ρ^B) − S(ρ), where S(ρ) = −tr{ρlog₂ ρ} is the von Neumann entropy and ρ^A(ρ^B) is the reduced density matrix of ρ for a system by partly tracing out subsystem A (B).

In the classical theory of probability, the conditional probability leads to an equal expression for the classical mutual information.^[1] In order to generalize this classical expression to quantum regime, we have to measure the subsystem B by a complete set of projectors {B_n}. The state of a quantum system based on the n-th measurement becomes ρ_n = (I ⊗ B_n)ρ(I ⊗ B_n)/p_n, where p_n = tr{(I ⊗ B_n)ρ(I ⊗ B_n)} denotes probability of obtaining the n-th outcome, and I is an identity operator for another subsystem. The density operator given by the above equation produced an alternative definition of the quantum conditional entropy S(ρ|{B_n)} = Σ_n p_nS(ρ_n). Therefore, according to this equation, the quantum mutual information can also be defined by J(ρ|{B_n)} = S(ρ_A)−S(ρ|{B_n)}). The two definitions of mutual information are equivalent in classical condition, but they are different in quantum situation. The main reason is that quantum has effects on the correlation between system A and B, and it provides an exact measurement for the quantum correlation, which has been called quantum discord.^[6] In fact, the classical correlation must be maximized between systems A and B as C(ρ) = max_{Bn} J(ρ|{B_n)}).^[6–7] The quantum discord is then defined as D(ρ) = I(ρ_A,ρ_B)−C(ρ).

In order to evaluate the quantum discord, we must maximize the classical correlation. In the following text, we give the obvious expression for a subclass of the X structure density matrix, which is often applied in quantum information theory. It can be taken the following form

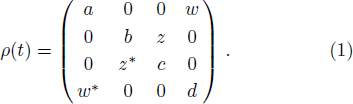
The diagonal elements are real and the others are complex numbers. It is quite easy to calculate S(ρ^A) and S(ρ^B). To calculate the quantum discord we need to maximize the classical correlation J(ρ|{B_n)}). Generally speaking, a one-qubit projector can be written as a function of two angles.^[22] By calculating, we can acquire the representation of quantum discord as follows

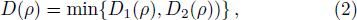
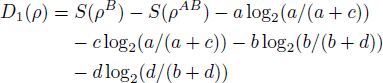
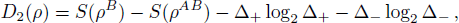
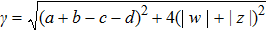
In the following, we focus our attention to a system which is composed of two non-interacting two-level qubits. Each qubit is coupled to an external environment, which is modeled as a boson.^[29] The Hamiltonian of the total system can be given by

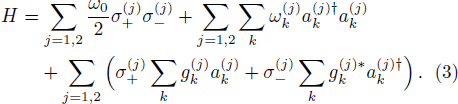
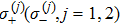
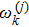
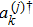
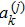
It should be noted that the Hamiltonian in Eq. (3) is quite versatile, which can be adopted to describe many different real systems. For example, in the field of quantum communication, two atoms in spatially separated cavities or two far enough Josephson charge, flux, or phase qubits are the sender and receiver. So, it is reasonable to assume that both interact with its own environment and there is no mutual interaction between them.

For simplicity, the two-qubit system begins a state with single excitation and both reservoirs are in their vacuum state, respectively. The state of the total system at time t > 0 can be written in the form

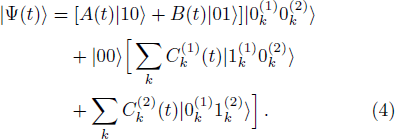
First, the interaction Hamiltonian in the Schrodinger picture is converted to the Hamiltonian in the Dirac picture, and then substituting equation (4) into the Schrodinger equation in the Dirac picture, we can obtain the following integer-differential equations

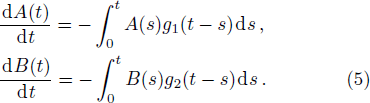
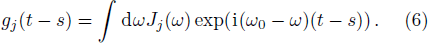
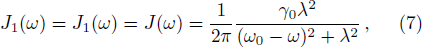
This problem can also be solved by means of the projector operator techniques.^[24] The NZ master equation in the second-order approximation is

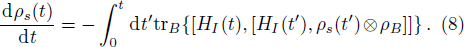
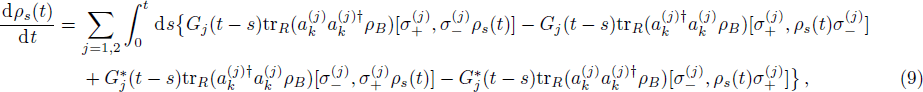
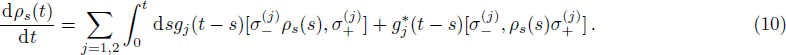
According to similar method, the second-order TCL master equation can be easily obtained with ρ_s(s) in the right part of Eq. (10) replaced by ρ_s(t). Given the spectral density J_j(ω), the reduced dynamics of two atoms can be solved numerically.

With the results above, we can study time evolution behavior of quantum discord in order to further test the range of effectiveness of the NZ and TCL approaches. Analytical quantum discord dynamics are presented as a reference.

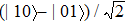
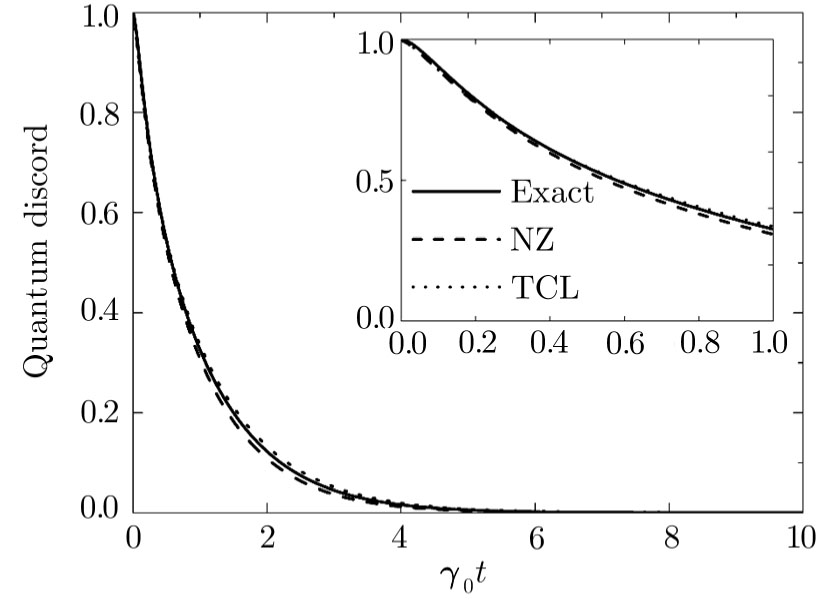First, we suppose that two atoms are initially in the Bell state , namely entangled state. In order to test the effectiveness of the NZ and TCL approaches, we explore three different regimes by varying the width λ of the Lorentzian spectrum. Figures 1–3 show the comparison of quantum discord dynamics among the exact, the NZ and TCL approaches, which correspond to three different values of λ. The value λ = 10γ corresponds to a Markovian regime, while λ = γ and λ = 0.01γ correspond to a weak and strong non-Markovian regime, respectively. This investigation will allow us to assess in which cases the solutions of the master equations are efficient in the description of the true dynamics of the system.

Fig. 1

	Figure Option ViewDownloadNew Window
	Fig. 1 The quantum discord dynamics for a system initially prepared in the Bell state 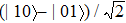, and the two reservoirs initially in vacuum states. The width of the Lorentzian spectral density is λ = 10γ.

In the Markovian limit, we can see clearly from the quantum discord showed in Fig. 1 that they are in perfect agreement with the exact, the NZ and the TCL solution for the short-time behavior but also for long interaction times. Therefore these two approximate approaches are better methods in the Markovian regime. The main reason is that both NZ and TCL are non-Markovian approachs and the history of quantum discord is taking into account. In addition, second-order approximation is proper in the weak coupling regime. It is worth to underline the initially quadratic behavior that witnesses the non-Markovian features of the dynamics of the system.

In the weak non-Markovian regime, just as shown in Fig. 2, despite the good agreement for the short-time dynamics, we can observe significant deviations when time increases between the exact and NZ solution. In other words, the NZ equation leads to a very bad approximation for the long-time behavior. The TCL solution coincides with the exact solution and completely agrees with the exact for long time. In short time, these three solutions are exactly the same (the inset of Fig. 2). The NZ solution appears zero at certain time spot and then revives gradually, which deviates from the exact solution. We can conclude that for this range of parameters the TCL solution gives a better description of the quantum discord dynamics since it reproduces all the qualitative features of the exact solution.

Fig. 2

	Figure Option ViewDownloadNew Window
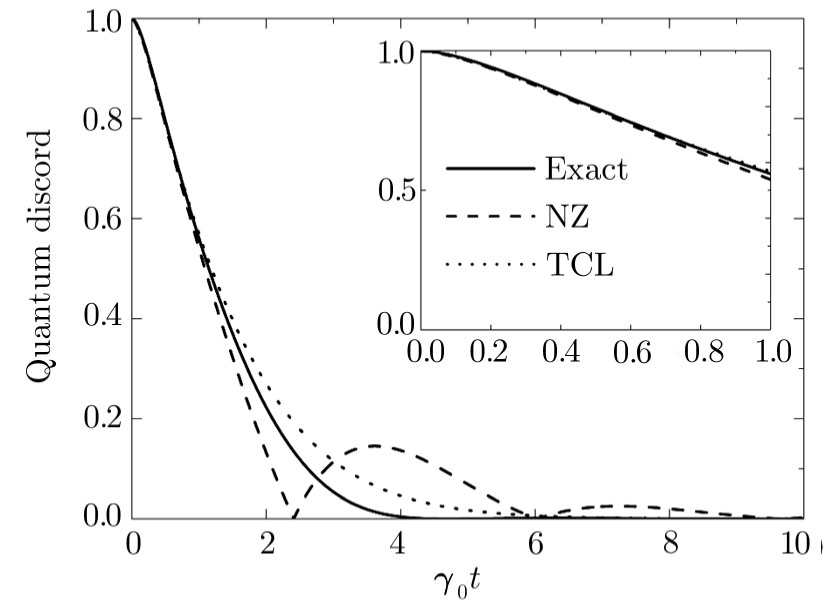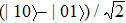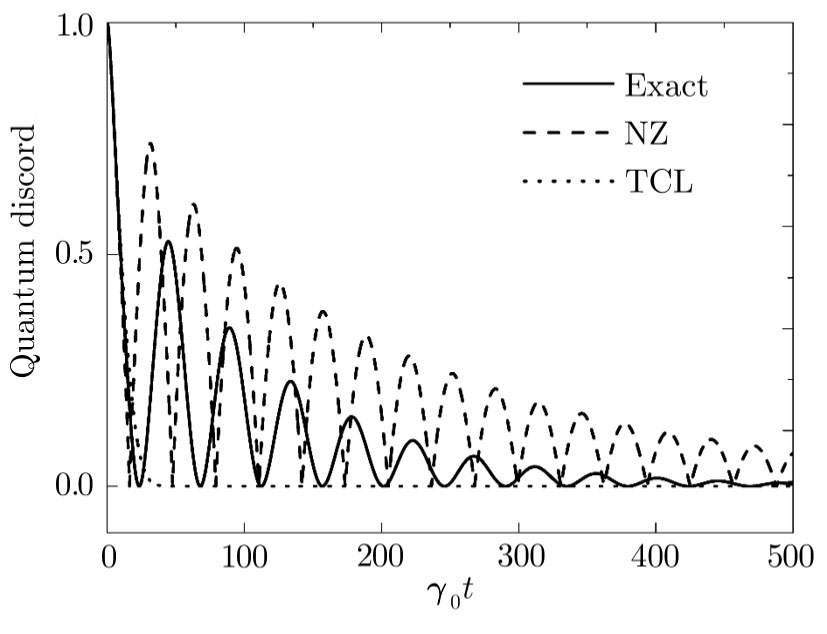	Fig. 2 The quantum discord dynamics for a system initially prepared in the entanglement state . The width of the Lorentzian spectral density is λ = γ.

Fig. 3

	Figure Option ViewDownloadNew Window
	Fig. 3 The quantum discord dynamics for a system initially prepared in the entanglement state 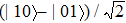. The width of the Lorentzian spectral density is λ = 0.01γ.

Finally, in the strong non-Markovian regime displayed in Fig. 3, we can observe a perfect agreement among all the three approaches in the short-time behavior, but the TCL approach is improper in the description of the quantum discord dynamics for the long-time behavior. It is not able to describe the behavior of Rabi oscillation. For the NZ solution, it also presents the behavior of oscillations and the behavior of quantum discord reaches zero in certain regime. Thus, in this case, both perturbative approaches are not suitable to describe the quantum discord dynamics of the system for long time.

How to descript properly of open quantum systems is still far from having a complete and general solution. On one hand, the TCL approach provides a generalized master equation which is local in time. On the other hand, the NZ solution provides a generalized master equation in which the time derivative of the density operator is connected to the past history of the state. Intuition tells us that NZ method provides better description of the memory effect than the TCL method, because it explicitly considers the past history of the open system. However, this is not the case. From the above analysis, we can know that it is difficult to establish whether one method is better than the other one. In fact, the performance of quantum discord dynamics of the system strongly depends on the details of the system, such as initial state, spectral density expressions, spectral width and so on.

In this paper we have presented a systematic comparison of different non-Markovian approaches to the dynamics of quantum discord for two non-coupled qubits interacting with independent reservoir. In particular, we further testify the range of validity of the NZ and the TCL master equation by exploiting this model, which can be applied to different coupling regime. Generally speaking, the TCL approach seems to be preferred to the NZ method when we study the quantum discord dynamics. The dynamics of quantum discord is better than the one that the entanglement gives in describing the quantum correlation.^{[8, 18]} Therefore, the comparison of the above mentioned may be better than the comparison of entanglement dynamics.^[30–31] We finally note that our model contains two non-coupled qubits and is universal in the fields of quantum communication. If the reservoirs are in the case of finite temperature or the thermal nonequilibrium, more proper approximation is demanded and the two dynamics methods need to be developed. These points will be the subject of our future research.