† Corresponding author. E-mail:
Supported by the Fundamental Research Funds for the Central Universities under Grant No. 2018MS132
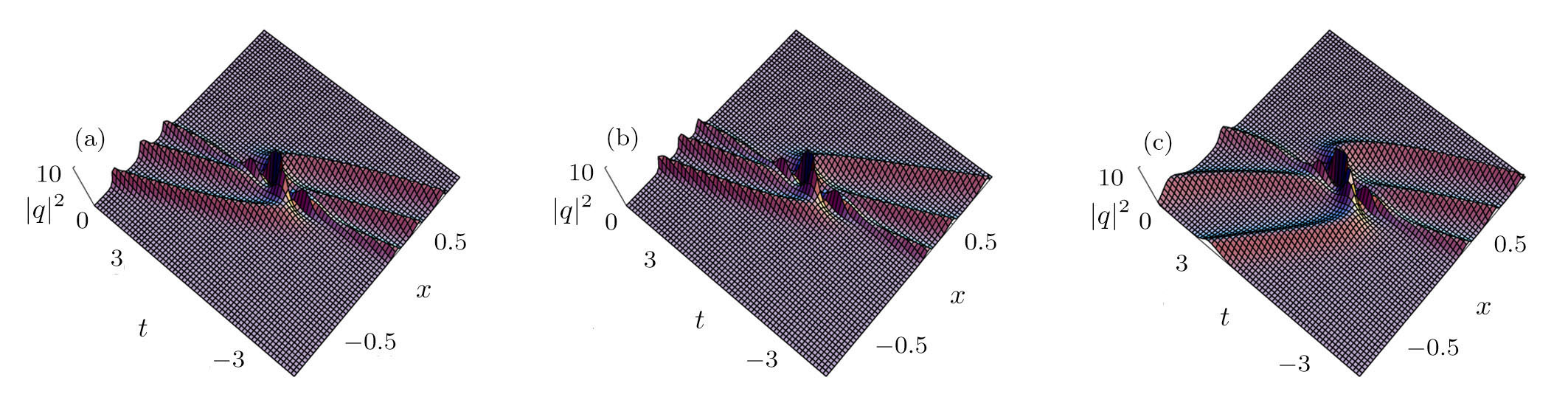
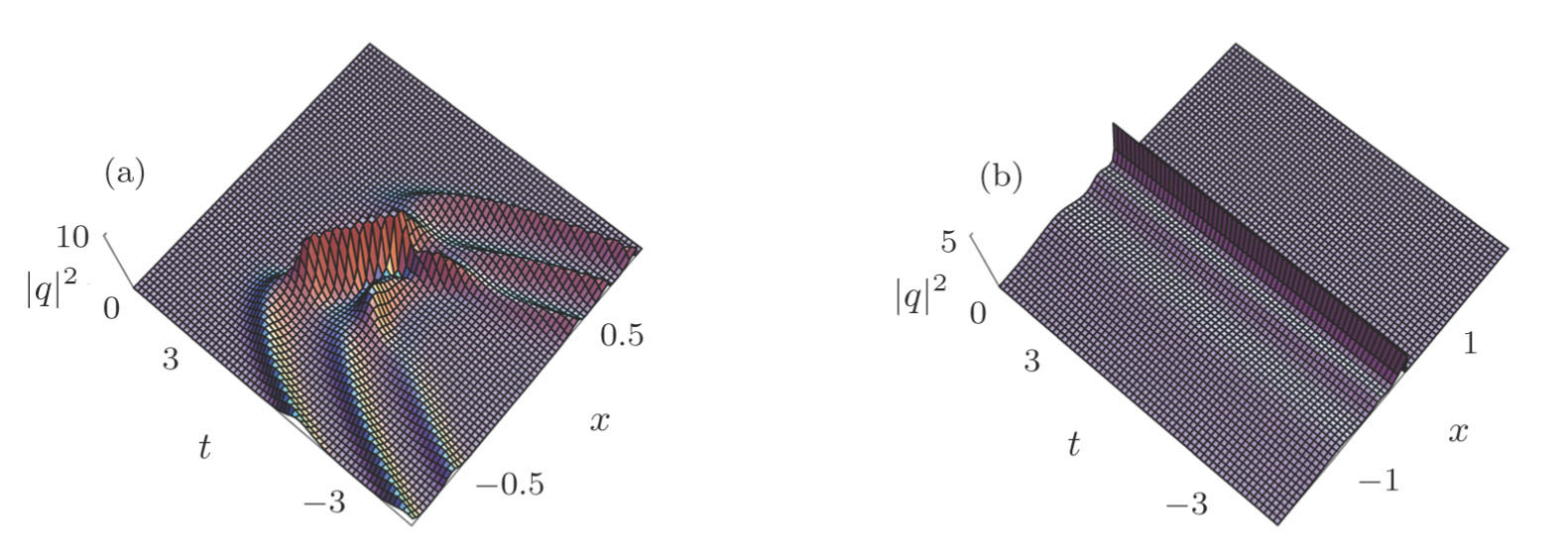
A generalized nonautonomous nonlinear equation, which describes the ultrashort optical pulse propagating in a nonlinear inhomogeneous fiber, is investigated. N-soliton solutions for such an equation are constructed and verified with the Wronskian technique. Collisions among the three solitons are discussed and illustrated, and effects of the coefficients σ1(x, t), σ2(x, t), σ3(x,t) and v(x, t) on the collisions are graphically analyzed, where σ1(x, t), σ2(x, t), σ3(x, t) and v(x, t) are the first-, second-, third-order dispersion parameters and an inhomogeneous parameter related to the phase modulation and gain(loss), respectively. The head-on collisions among the three solitons are observed, where the collisions are elastc. When σ1(x, t) is chosen as the function of x, amplitudes of the solitons do not alter, but the speed of one of the solitons changes. σ2(x, t) is found to affect the amplitudes and speeds of the two of the solitons. It reveals that the collision features of the solitons alter with σ3(x, t) = −1.8x. Additionally, traveling directions of the three solitons are observed to be parallel when we change the value of v(x, t).
As the solution of the nonlinear evolution equations(NLEE), soliton has caused many interests, since it plays an important role in some fields of science and engineering such as the nonlinear optics, Bose-Einstein condensates, fluid mechanics and plasma physics.[1–5] Soliton is self-localized, robust, long-lived, and preserves the identity, when it travels in a nonlinear, dispersive medium.[6–7]
N-soliton solutions can be derived with the Hirota method and Darboux transformation, and they can be expressed as an N-th order polynomial in the N exponentials.[8–10] However, it is difficult to verify such N-soliton solutions, but the solutions in the Wronskian-form are relatively easier to be differentiate.[8–9,11] Therefore, the Wronskian solutions can be verified by virtue of the direct substitution into bilinear forms of the NLEE.[11–12]
It has developed the classical soliton concept for the nonlinear and dispersive systems that have been autonomous, which means that the time is the only factor that plays the role of the independent variable, and the solitary waves in nonautonomous nonlinear and dispersive systems can propagate in the form of nonautonomous solitons.[13–15] Under investigation in this paper is the following generalized nonautonomous nonlinear equation,[16–18]
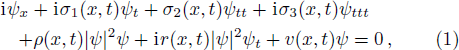
However, the N-soliton solutions for Eq. (
Bilinear forms for Eq. (
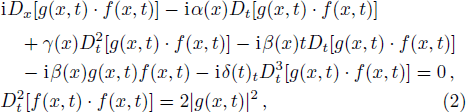
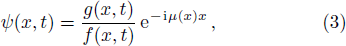
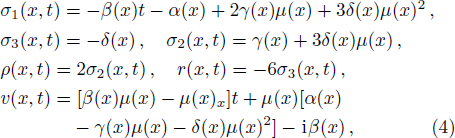
The double-Wronskian determinant is defined as
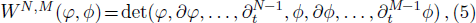
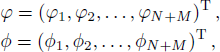
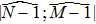
Considering the Lax pair of Eq. (
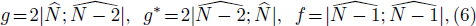
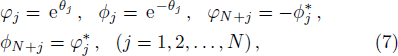
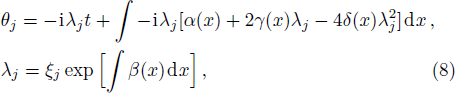
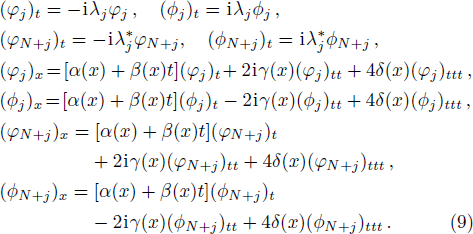
Based on the Wronskian technique, it can be proved that g and f defined in the double-Wronskian-form (
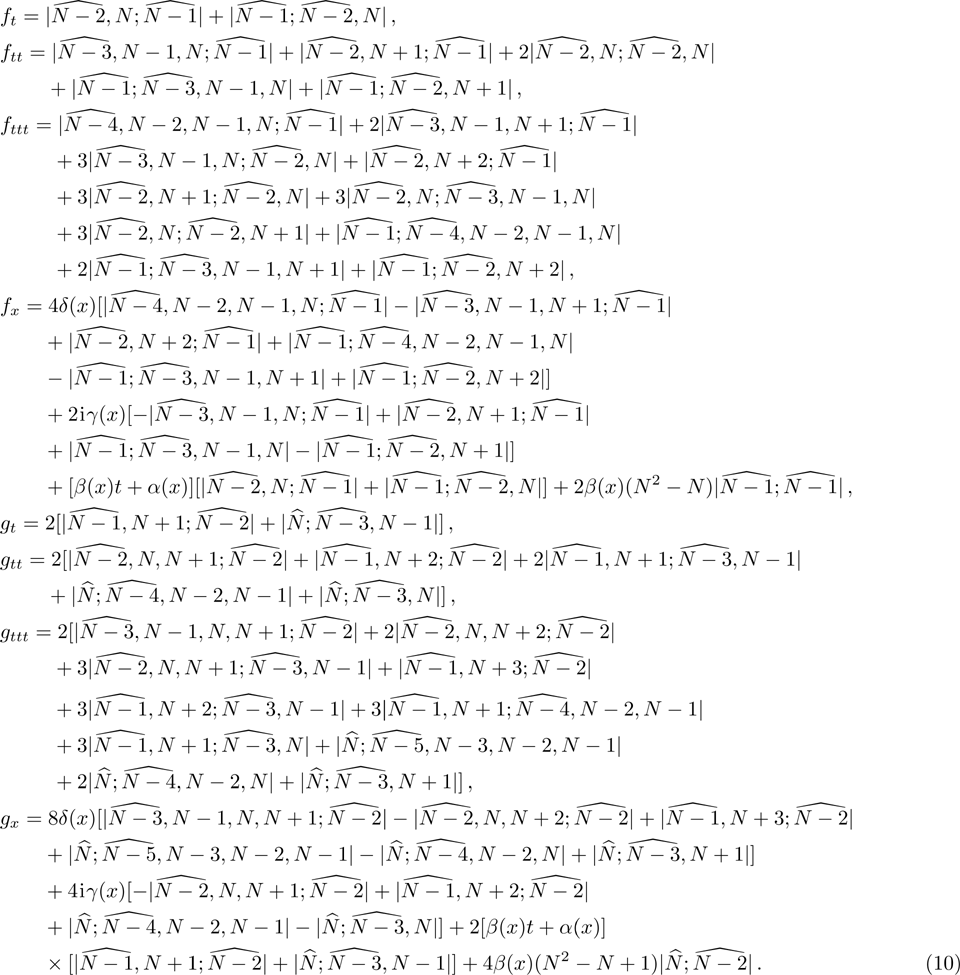
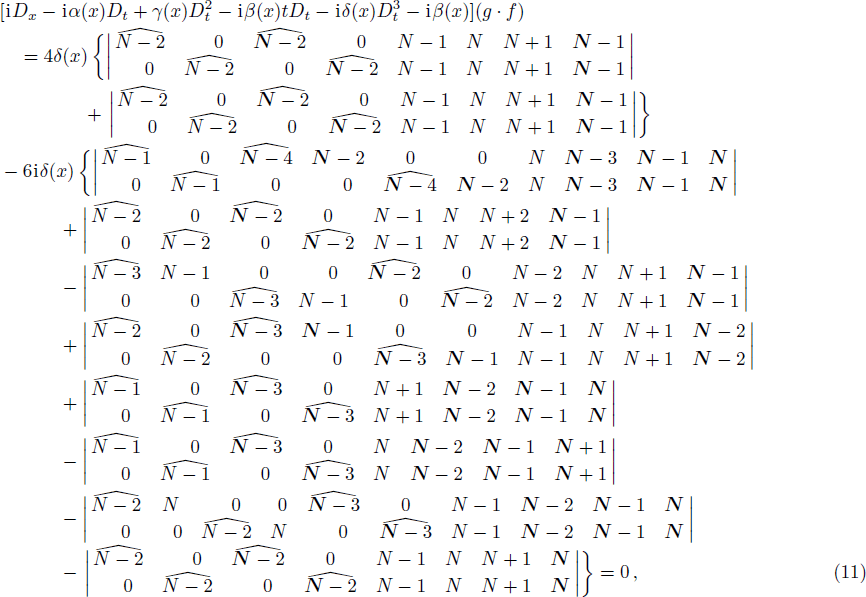
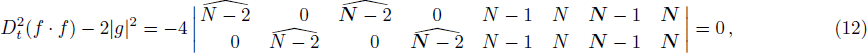
Up to now, we have verified that g and f defined in the doubele-Wronskian-form (
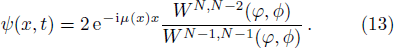
For N = 1, the bright one-soliton solution is given as
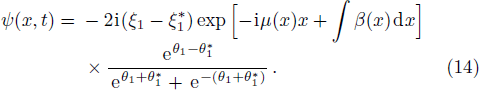
For N = 2, the two-soliton solutions are shown as
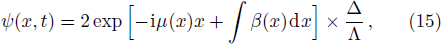
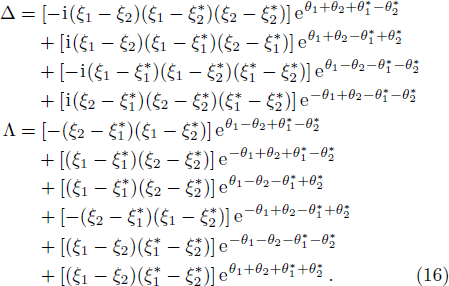
Similarly, we can obtain the expressions of the three- and four-soliton solutions, even the N-soliton solutions for Eq. (
Since the propagation of the one solitons and collisions between the two solitons have been investigated in Ref. [18], we will study the collisions among the three solitons in this section. Also, influences of σ1(x,t), σ2(x,t), σ3(x,t) and v(x,t) on the collisions are graphically discussed.
In Fig.
In conclusion, a generalized nonautonomous nonlinear equation (i.e., Eq. (
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] |