Cite this Article
Valverde Clodoaldo, Rodrigues Vaz Gabriela, de Oliveira Vitor Teles, Baseia Basílio. Statistical Properties of a System Consisting of a Superconducting Qubit Coupled to an Optical Field Inside a Transmission Line. Communications in Theoretical Physics, 2018, 69(6): 727  
Permissions
Statistical Properties of a System Consisting of a Superconducting Qubit Coupled to an Optical Field Inside a Transmission Line
Valverde Clodoaldo1, 2, *, Rodrigues Vaz Gabriela1, de Oliveira Vitor Teles1, Baseia Basílio3, 4
Campus de Ciências Exatas e Tecnológicas, Universidade Estadual de Goiás, BR 153, km 98, 75.132-903 Anápolis, GO, Brazil
Universidade Paulista (UNIP) - 74.845-090, Goiânia, Goiás, Brazil
Instituto de Física, Universidade Federal de Goiás - 74.001-970, Goiânia, Goiás, Brazil
Departamento de Física, Universidade Federal da Paraíba - 58.051-970, João Pessoa, Paraíba, Brazil

 

† Corresponding author. E-mail: valverde@ueg.br

Abstract
Abstract

The present work investigates the entropy and the excitation inversion of a coupled system that consists of a qubit represented by a Cooper pair box (CPB) interacting with a transmission line working as a circuit quantum electrodynamics (CQED). The proposed scheme uses the Buck-Sukumar model with a time dependent frequency in the presence of losses to study the evolution of the entropy and the excitation inversion of the system. We have shown that the CQED is much more sensitive to the presence of losses than the CPB. The results also show that it is possible to monitor properties of the subsystems through appropriate choices of the time-dependent parameters.

Keyword:excitation inversion;transmission line;entropy;Buck-Sukumar model
1 Introduction

The processing of quantum information in hybrid systems has gained great interest in the last years.[1–2] These systems combine with advantages atoms, spins, and solid-state devices with various applications, e.g., quantum computation and quantum information.[3–4] They are also advantageous in view of their compatibilities with individual subsystems and may offer potential opportunities to overcome obstacles in quantum states engineering.[5–8] One important example of hybrid systems is given by the arrangement of a Cooper pair box (CPB) qubit interaction with a circuit quantum electrodynamics (CQED) device.[9–11] The CQED opens a new frontier to study the ultra-strong coupling between “atoms” and individual microwave photons,[12] being also a potentially powerful architecture for quantum information and construction of the quantum computer.[13] Similar systems exhist, as one that employs a quantum optomechanical cavity,[14] which allows the manipulation and detection of mechanical movements in the quantum regime, as creation of non classical states using light. All these approaches form a basis for applications in quantum information, where optomechanical devices can serve as interfaces between radiation and matter. It is also possible to construct hybrid quantum devices that combine infinite degrees of freedom from different physical systems. All these systems offer an alternative to fundamental tests of quantum mechanics in a regime of inaccessible parameters of size and mass.[14–17]

Hybrid systems have been explored in several works, e.g.: in the study of Bose-Einstein condensates,[18] photon blockade,[19–20] propagating phonons,[21] atomic physics and quantum optics,[22–23] quantum dynamics,[24] and quantum circuits combined with electronic spins.[25] Among the many concerning works,[23,26–29] few of them treat the influences of time dependent parameters, as frequency and amplitude, upon the properties of the system.[30–31] According to Refs. [32–33] these influences upon the coupling rate of the subsystems can be determined by the optical mass detection technique; a recent review on cavity-field coupled to optomechanics is given in Ref. [17].

In this work we have employed the (intensity-dependent) Buck-Sukumar model (BS)[34] to treat this coupled system where a superconducting CPB works as qubit interacting with a transmission line working as a CQED[35–36] in presence of losses[37] and under the action of a time dependent external field. The BS model was proposed in attention to a result obtained by Eberly et al.[38] using the original Jaynes-Cummings model (JC) to treat the coupled CPB system with the CQED, the first assumed in its ground state and the second in a coherent state: it was found that, for large times, the oscillations of the CPB excitation inversion could only be obtained combining numerical techniques with analytical approximations; the scenario became even more complicated for fields (CQED) starting from a thermal state, with no solution in the original JC model. Contrarily, the BS offered exact solutions.[34,38] As one should expect from Eq. 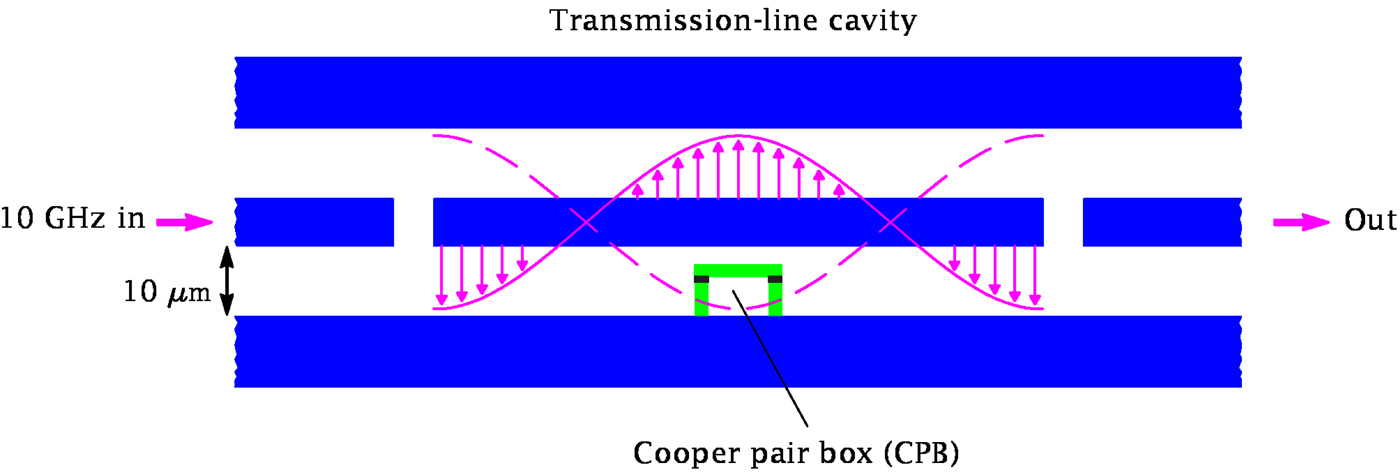(3) below, the results using BS and JC models coincide when the CQED has low intensity, which corresponds to small values of number averages < 10. According to Ref. [39], although its experimental realization seems to be not feasible in the domain of quantum optics, it may be simulated in arrays of coupled waveguides.[40] This new model was used by many authors in different scenarios, e.g., Ref. [41], including an interpolation between it and the JC model.[39] In both situations the BS model offered an exact solution. Another such interpolation was considered recently.[42]

In the present CPB-CQED configuration Fig. 1 we investigate the evolution of the CPB excitation inversion and statistical properties of both subsystems. The influence caused by losses and external forces upon these two properties is also considered. The relationship between the entropy and the degree of state mixing that occurs during the system evolution is also discussed. The paper is outlined as follows. In Sec. 2 we present the physical arrangement and the hamiltonian for our coupled system, including the basic theoretical procedures. In Sec. 3 we describe the evolution of CPB excitation inversion and entropy of the system. Section 4 contains the results and discussion and Sec. 5 includes the comments and conclusion.

Fig. 1 (Color online) Schematic of the arrangement to investigate the system. In it a superconducting qubit (green) interacts with the electric field (pink), both inside a transmission line (blue); the latter consists of a central conductor and two ground planes on either side.
2 Model of the COPB-CQED System

The CQED is implemented through a transmission line resonator whose electric field is coupled to a superconducting CPB, as shown in Fig. 1. The scheme is inspired by the works in Refs. [36, 43–44]. The CPB is positioned at the antinodes of the first harmonic standing wave electric field. The transition frequency between the ground |g⟩ and first excited state |e⟩ of CPB is approximately given by,

and is controllable through the flux-dependent Josephson energy,

Here we consider ħ = 1 and assume the two Josephson junctions of the CPB with the same energy EJ; Φ is the external flux; EJ and EC stand respectively for the energy of each Josephson junction and the charge energy of a single-electron EC = e2/(C1 + 2CJ); EJmax stands for the maximum Josephson energy at flux Φ = 0 whereas Φ0 = h/2e is the magnetic quantum flux. The parameters C1 and CJ stand for the input capacitance and the capacitance of each Josephson tunnel, respectively.[36,43–44]

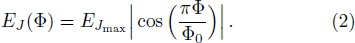
Thus, we can write the Hamiltonian of the total system in the form,

where â†(â) stands for the creation (annihilation) operator of the field with frequency ω; is the rasing (lowering) operators acting opon the CPB, is a Pauli operator given below, ωc is the CPB frequency, and λ0 stands for the coupling strength between CPB and CQED. We use the Pauli’s matrices to describe the action of operators on the two-level CPB system. As mentioned above we have,

where the state |g⟩ (|e⟩) stands for the ground (excited) state of the CPB. Here we will consider a more general scenario replacing ω → ω(t) = ω0 + f(t) and λ0 → ζ(t) = λ(1 + f(t)/ω0)1/2, with ω0 being the natural frequency of the CQED and f(t) is an external agent coupled to CQED. In this context we also consider the presence of losses in the system, as follows,

where ω(t) is a time dependent frequency, γ and δ stand for the CPB decay constant and the loss of the CQED, respectively.

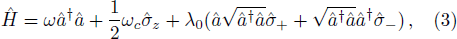
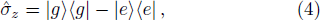
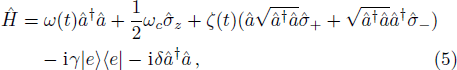
The state |Ψ(t)⟩ describing the time evolution of the entire system can be written as,

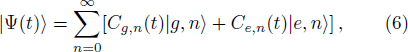
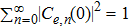
where |g⟩ (|e⟩) represents the CPB in its ground (excited) state and n stands for the number of excitation in the CQED. Throughout this study we will assume the CPB initially prepared in the excited state |e⟩ and the CQED in a superposition of two coherent states, |Ψ⟩ = η(|α⟩ + | − α⟩), where η = [2 + 2e−2α2]−1/2 is the normalization factor. We also assume the CPB state initially normalized, hence and the initial condition Cg,n(0) = 0. As usually, we assume the subsystems CQED and CPB decoupled at t = 0.

The evolution of the wave function described by Eq. (6) is obtained via the solution of the Schrödinger equation,

Substituting the Eq. (5) and Eq. (6) in Eq. (7) we find the pair of coupled equations,

Solving this coupled system by the 4-th order Runge-Kutta numerical method, we obtain the coefficients Ce,n(t) and Cg,n+1(t). This allows us to determine the dynamic properties of the system, e.g., those related to the CPB excitation inversion and the entropies of both subsystems.

3 Evolution of CPB Excitation Inversion and Entropy

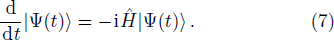
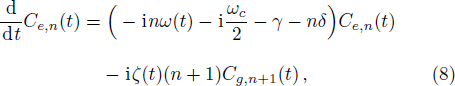
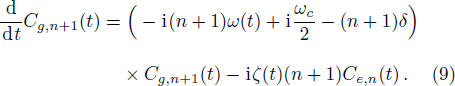
The CPB excitation inversion, I(t), here is given by the form,

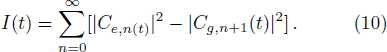
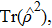
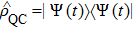
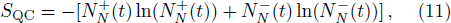
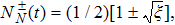
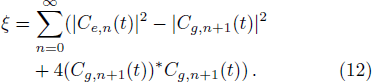
The effect concerns the population transition between the fundamental and excited levels of CPB. On the other hand, the von Neumann’s entropy offers a quantitative measure of the disorder of a system as well as its degree of impurity, as shown by Phoenix and Knight.[45] This kind of entropy, defined in the form SQC = −Tr(ρQC ln (ρQC)) is a measure of the entanglement of two (or more) subsystems. Here the term entanglement is used with the meaning of mixed state, whose measure is given by instead of the more usual meaning of correlated quantum states in the EPR sense.[46] The density operator ρQC describing the entire system can be defined as ; thus the entropy takes the form,

where,

The entropy SQC(ρQC) is zero when ρQC represents a pure state and is maximum and equal to ln(N) for a state of maximum mixing, where N is the dimension of the Hilbert space. However, here our state is pure only at t = 0; for t > 0 the state of the whole system ceases to be pure due to the presence of losses and the eventual action of time-dependent external fields. 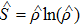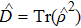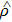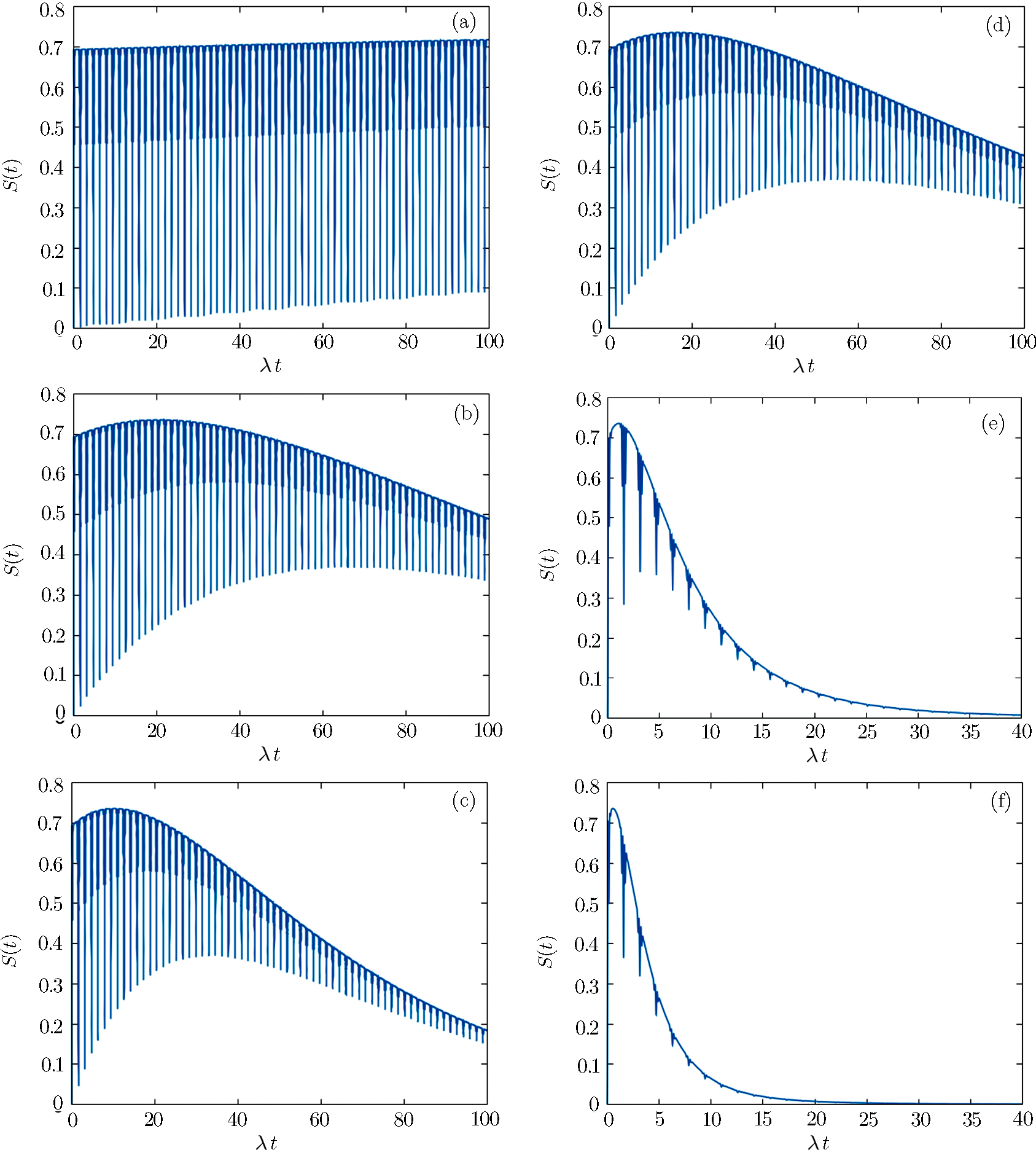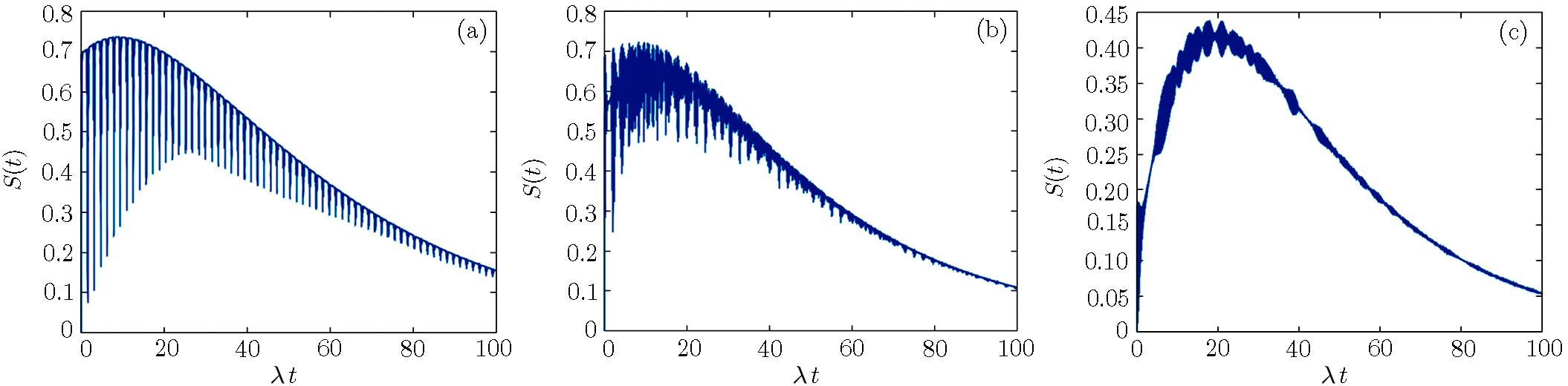Now, concerning the relationship between the entropy and the degree of mixing of the state, , despite having this relation between Ŝ and , to our knowledge the connection between these two quantities, Ŝ and , is not trivial.

4 Results and Discussions
4.1 Entropy: (a) Resonant Case

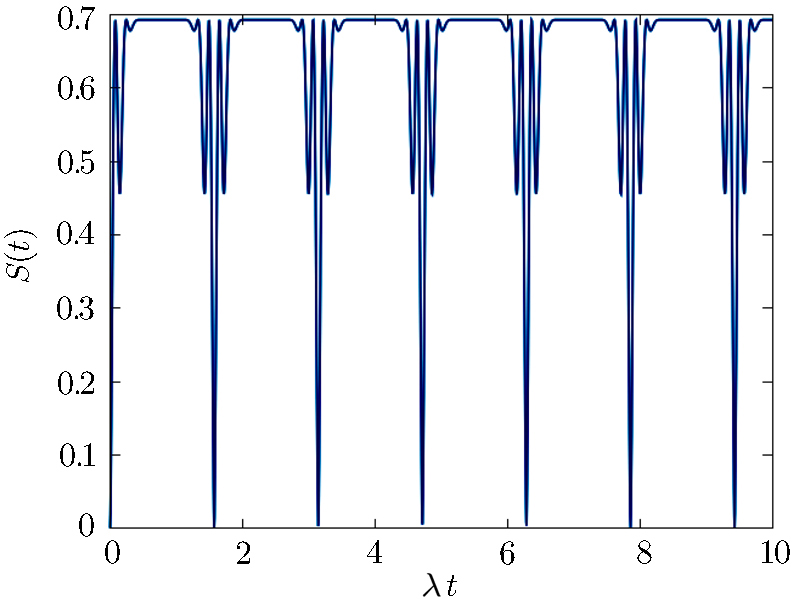We will initially analyze the entropy of the system in the absence of losses for the superposition of coherent states {|α⟩}, for |α| = 3. Figure 2 shows the changes that repeat in the period T ≈ 1.58λt while the entropy presents a maximum value 0.7.

Fig. 2 Time evolution of the entropy for the QED-circuit initially in a superposition of coherent states, in the resonant case, for |α| = 3.0, ω0 = 2000λ and ω = 2000λ.

Figure 3 shows the entropy as a function of the dimensionless time λt: in the first column, going from Figs. 3(a) to 3(c), we vary the parameter γ and fix δ = 0.0; in the second column we set γ = 0.0 and vary δ. The time evolution of the entropy was observed in the presence of loss affecting only the CPB while in Figs. 3(d) to 3(f) the entropy evolves with losses affecting only the CQED. Comparing Figs. 3(a) with 3(d), 3(b) with 3(e), and 3(c) with 3(f), we note that the higher influence on the entropy occurs when the loss is included in the CQED, than when caused by the loss in the CPB. Based on the results by Refs. [47] and [48] the decoherence effect is greater in CQED due to the fact that this subsystem can be more excited than the CPB. The reverse only occurs for very low average excitation of CQED, . As expected, in both cases the maximum value of entropy increases when losses are included (see Figs. 2 and 3).

Fig. 3 Time evolution of the entropy of the QED-circuit initially in a superposition of coherent states, for |α| = 3.0, ω0 = 2000λ and ω = 2000λ: (a) γ = 0.001λ and δ = 0.0; (b) γ = 0.015λ and δ = 0.0; (c) γ = 0.030λ and δ = 0.0; d) δ = 0.001λ and γ = 0.0; (e) δ = 0.015λ and γ = 0.0; (f) δ = 0.030λ and γ = 0.0.

Another detail observed is that, for the ratio γ/δ ≈ 16 between the decays the influences on the entropy are quite similar for |α| ≤ 3 (Fig. 4). On the other hand, while the CQED state loses its coherence, its entropy tends to zero rapidly (see Fig. 3(e)).

Fig. 4 (Color online) Time evolution of the entropy of the QED-circuit initially in a superposition of coherent states, with |α| = 3.0, ω0 = 2000λ and ω = 2000λ. The blue region stands for: γ = 0.0 and δ = 0.001λ; the yellow region is for δ = 0.0 and γ = 0.015λ.
4.2 Entropy of the System: (b) Non Resonant Case

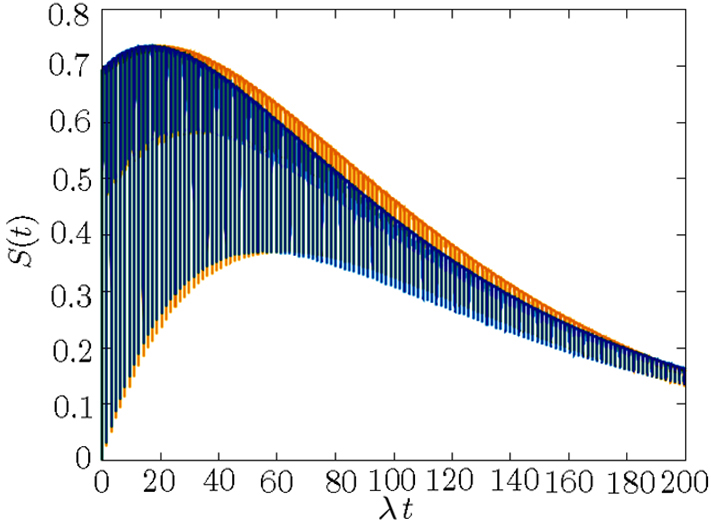
Here the subsystems are assumed non resonant, with fixed detuning f(t) = η. The entropy in absence of loss is smaller than in its presence and the periodicity disappears when detuning increases (Fig. 5). In absence of losses, detuning affects the entropy of both subsystems, causing a decrease in its maximum value; this effect is amplified in presence of losses (see Fig. 6). The amplitude of the entropy decreases whenever the detuning is large, η ≫ 1.

Fig. 5 Time evolution of the entropy of the QED-circuit initially in a superposition of coherent states, with |α| = 3.0, ω0 = 2000λ, ω = 2000λ, and γ = δ = 0.0; (a) for η = λ; (b) for η = 20λ; (c) for η = 100λ.
Fig. 6 Time evolution of the entropy of the QED-circuit initially in a superposition of coherent states, with |α| = 3.0, ω0 = 2000λ, ω = 2000λ, γ = 0.015λ, and δ = 0.001λ (a) for η = λ; (b) for η = 20λ; (c) for η = 100λ.

The entropy of the system in presence of losses and a time-dependent detuning (f(t) = η cos(ω′t)) has an opposite effect to what happens when f(t) = η = const. One observes that a variable detuning causes no decrease in the maximum value entropy of the system, as shown in Fig. 7.

Fig. 7 Time evolution of the entropy of the QED-circuit initially in a superposition of coherent states, with |α| = 3.0, ω0 = 2000λ, ω = 2000λ, γ = 0.015λ, δ = 0.001λ, and η = 100λ (a) for ω′ = 10; (b) for ω′ = 20; (c) for ω′ = 50.
4.3 CPB Excitation Inversion: (a) Resonant Case

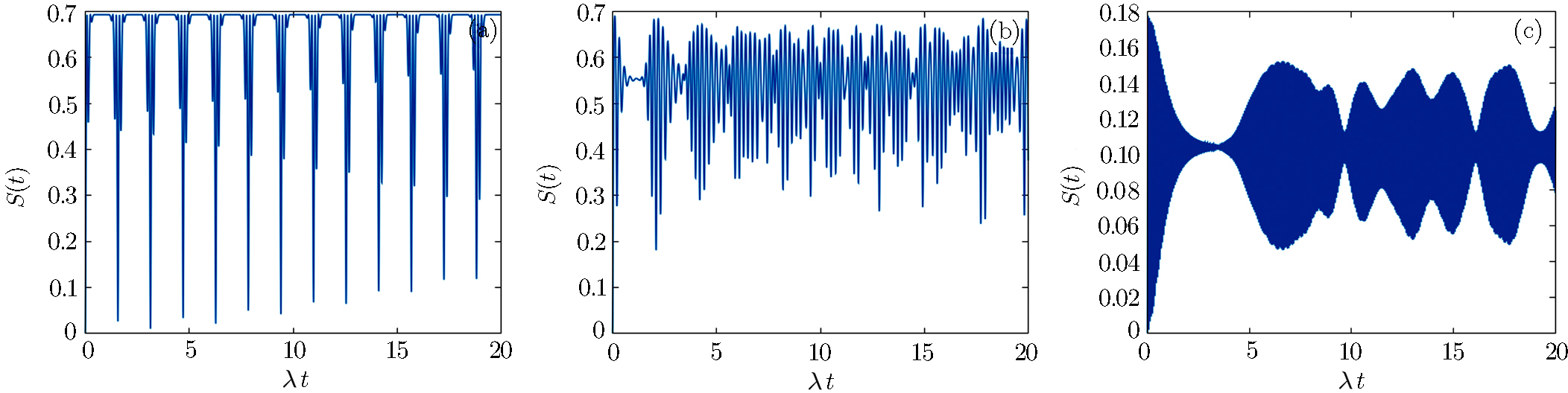
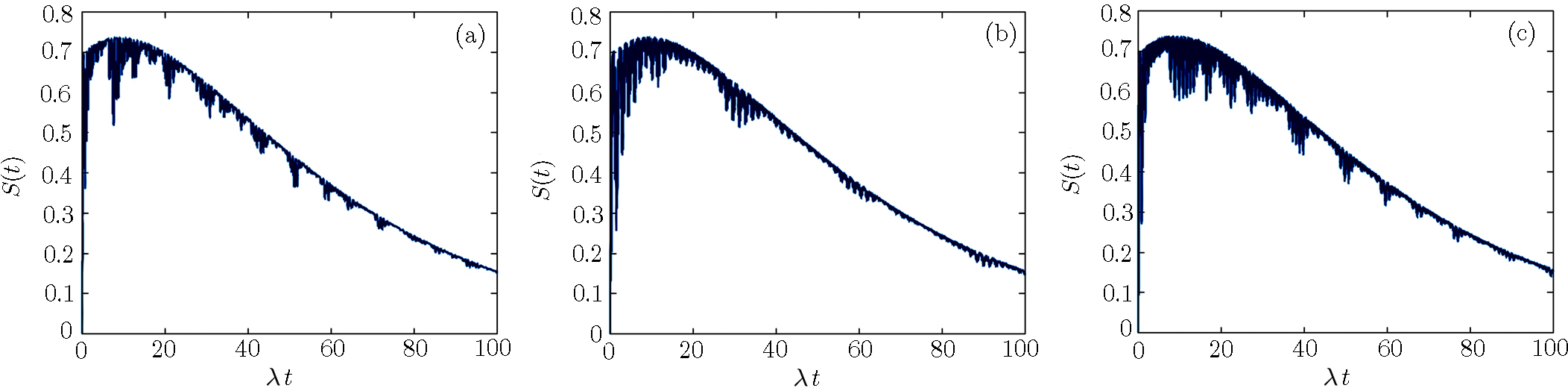
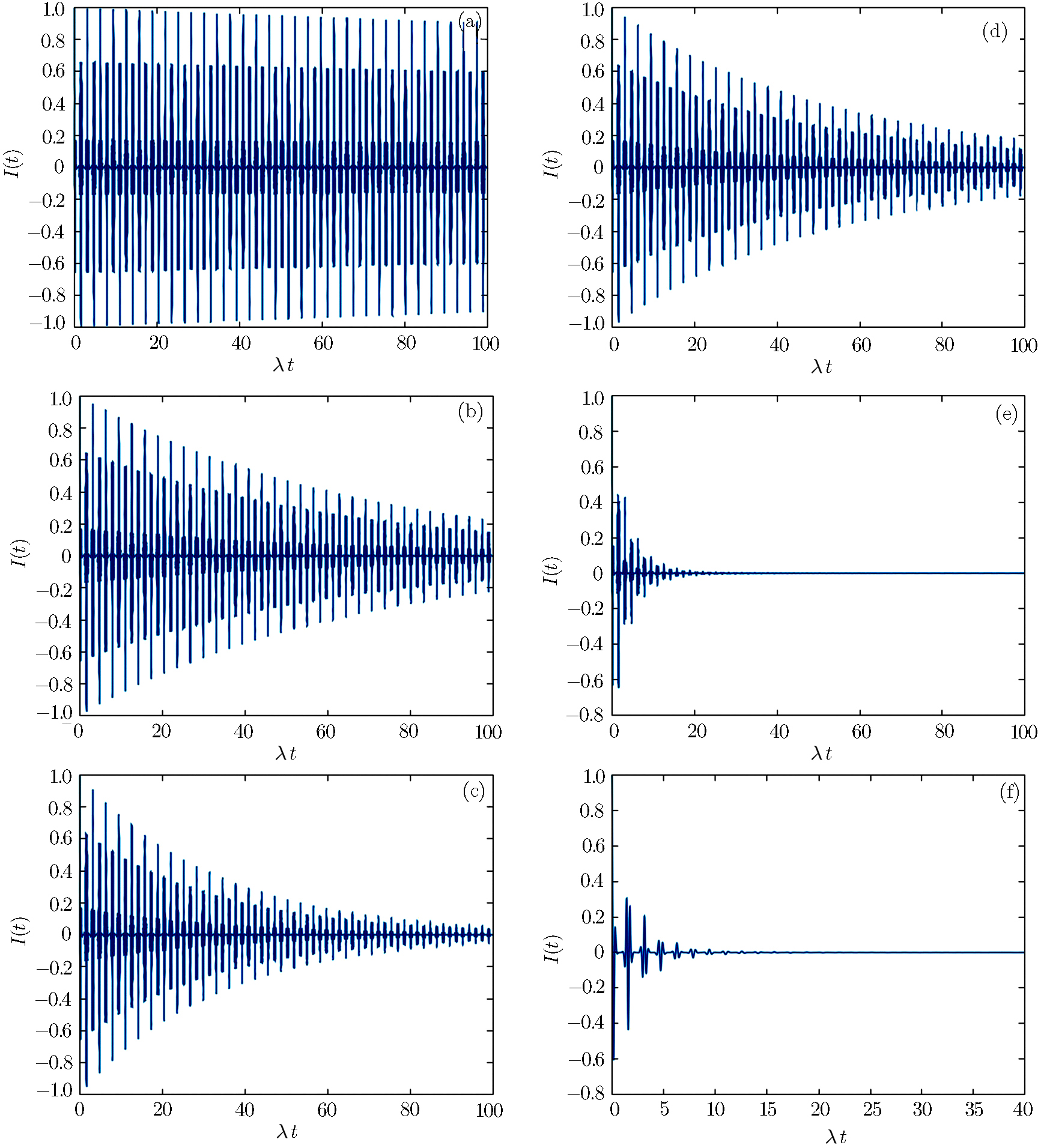
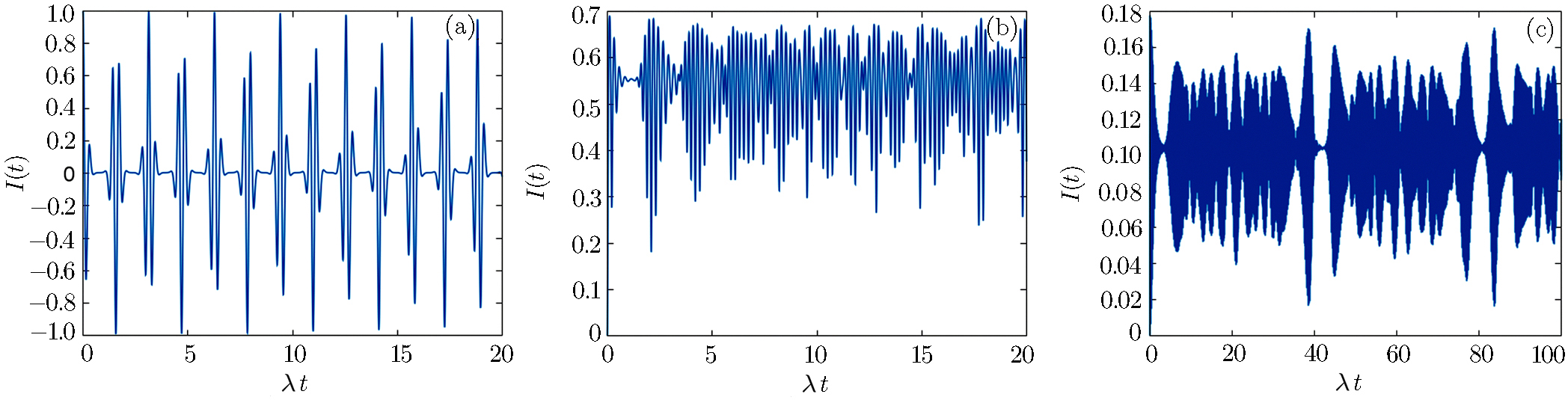
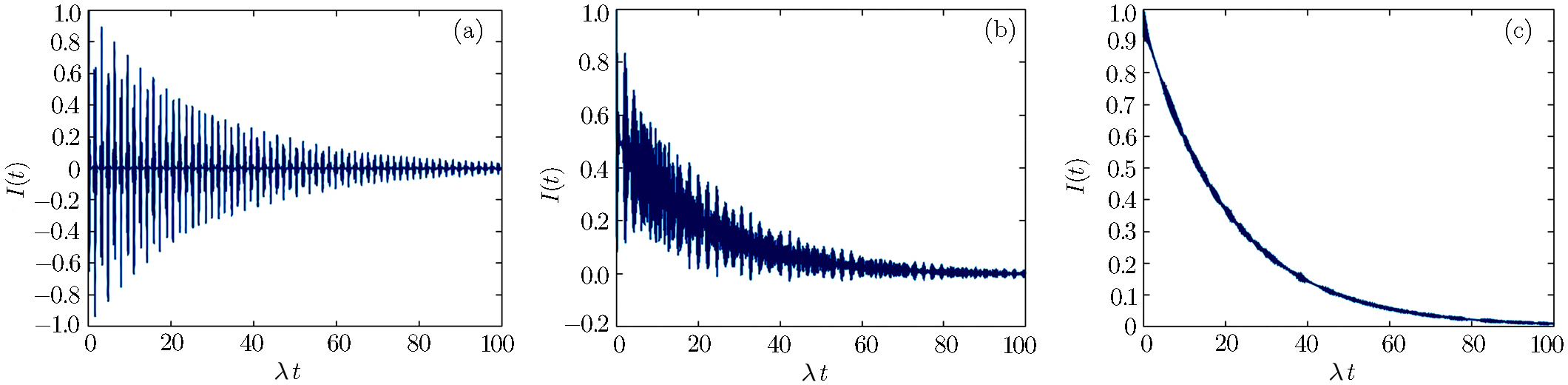
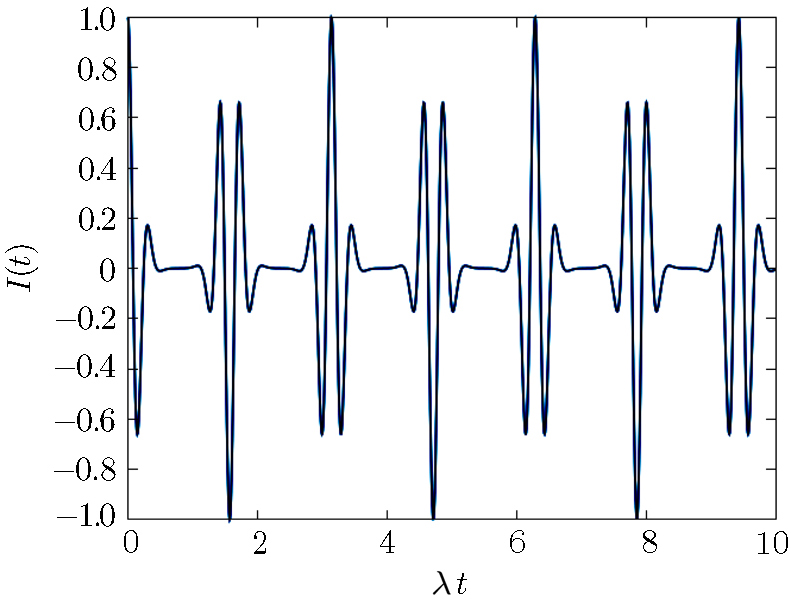Firstly we consider the CPB in absence of losses and the field state in the mentioned superposition of two coherent states, for |α| = 3.0; according to Fig. 8 no collapse and revival effect is shown in the CPB excitation inversion.

Fig. 8 Time evolution of the excitation inversion for the QED-circuit initially in coherent state superposition, with |α| = 3.0, ω0 = 2000λ, and ω = 2000λ.

Figure 9 shows the excitation inversion as a function of (dimensionless) time (λt): in the first column, going from Figs. 9(a) to 9(c) we let γ to vary and set δ = 0.0; in the second column we set γ = 0.0 and let δ to vary. Comparing Figs. 9(a) with 9(d), 9(b) with 9(e) and 9(c) with 9(f) we see again that the loss affecting the CQED has a greater influence on the inversion of excitation of the CPB. As the CQED can be more excited than the CPB, the deleterious effect of losses is greater in the CQED; for the ratio γ/δ ≈ 16 between the decays, the influences of losses on the excitation inversion are quite similar for any |α| ≤ 3.

Fig. 9 Time evolution of the excitation inversion for the QED-circuit initially in coherent state superposition, with |α| = 3.0, ω0 = 2000λ, and ω = 2000λ; (a) for γ = 0.001λ and δ = 0.0; (b) γ = 0.015λ and δ = 0.0; (c) γ = 0.030λ and δ = 0.0; (d) δ = 0.001λ and γ = 0.0; (e) δ = 0.015λ and γ = 0.0; (f) δ = 0.030λ and γ = 0.0.
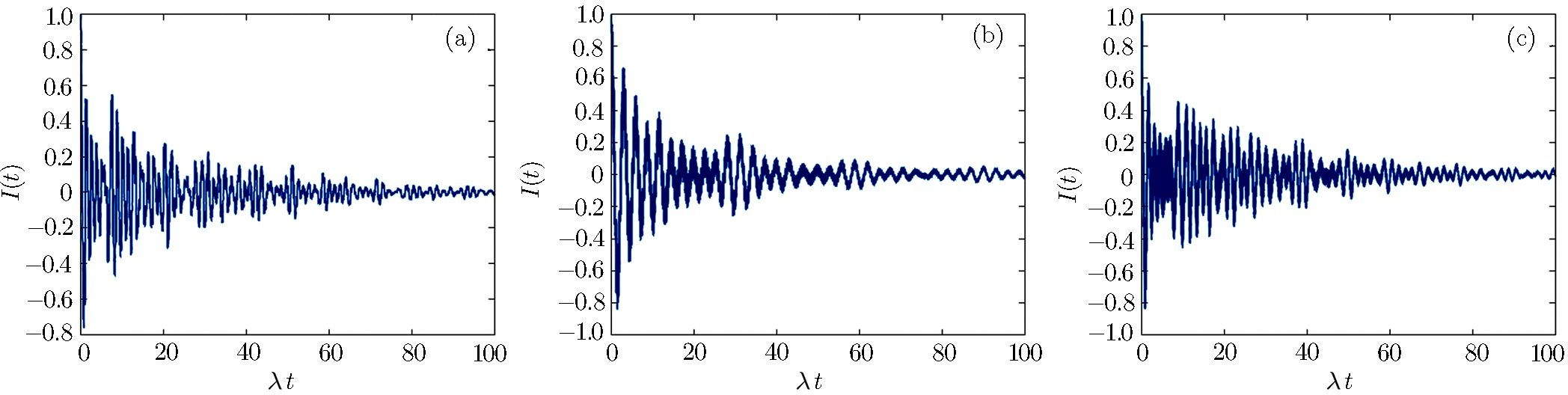
4.4 CPB Excitation Inversion: (b) Non Resonant Case

Here the subsystems are assumed non resonant with constant detuning f(t) = η. The excitation inversion in absence of losses is greater than in their presence and the periodicity disappears when detuning increases (Fig. 10). Detuning affects the excitation inversion of the CPB by decreasing the maximum amplitude value, the same effect is observed in entropy (see Fig. 5). Excitation inversion in the CPB does not occur for large detuning (η ≫ 1). When the system is in the presence of losses the excitation inversion occurs only for small detuning values, see Fig. 11(a), for higher detuning values there is no occurrence of excitation inversion; see Figs. 11(b) and 11(c).

Fig. 10 Time evolution of the excitation inversion for the QED-circuit initially in coherent state superposition, with |α| = 3.0, ω0 = 2000λ, ω = 2000λ, and γ = δ = 0.0; (a) for η = λ; (b) for η = 20λ; (c) for η = 100λ.
Fig. 11 Time evolution of the excitation inversion for the QED-circuit initially in coherent state superposition, with |α| = 3.0, ω0 = 2000λ, ω = 2000λ, γ = 0.015λ, and δ = 0.001λ; (a) for η = λ; (b) for η = 20λ; (c) for η = 100λ.

The evolution of excitation inversion of the system in the presence of losses with a variable detuning (f(t) = η cos(ω′t)) shows an opposite behavior to that for f(t) = η = constant. Now the time dependent detuning causes no extinction of the excitation inversion, i.e., the system continues reversing the excitation but maximum value amplitude of inversion decreases with time, as shown in Fig. 12.

Fig. 12 Time evolution of the excitation inversion for the QED-circuit initially in coherent state superposition, with |α| = 3.0, ω0 = 2000λ, ω = 2000λ, γ = 0.015λ, δ = 0.001λ, and η = 100λ; (a) for ω′ = 10; (b) for ω′ = 20; (c) for ω′ = 50.
5 Conclusion

In this work we studied the dynamic properties (entropy of both sub-systems and the CPB excitation inversion) of a hybrid system composed of a CPB and an CQED. We considered the CPB initially excited and the CQED as a superposition of two coherent states. We have assumed the CPB-CQED system described by an intensity-dependent interaction introduced by Buck-Sukumar model. Concerning the entropy, which is related to the entanglement of subsystem states, we studied its time evolution in the presence of losses affecting both subsystems, for resonant and non-resonant cases. The influence on the entropy of a time-dependent (sinusoidal) frequency, via the CQED, was also considered. The excitation inversion was investigated under the same conditions and influences. The inclusion of losses in CPB and CQED makes the scenario more realistic. We have shown that the CQED subsystem is much more sensitive in the presence of losses than the CPB, this can be explained, due to the fact that the CQED presents a much larger number of photons in relation to the CPB. In addition, the time dependence of the coupling λt and CQED frequency ω(t) brings our results to different physical conditions. It was shown that the CPB excitation inversion occurs when detuning is constant in time; however, when it varies the excitation inversion always occurs no matter the value of detuning. In this hybrid system it is possible to control the entropy and inversion of excitation by choosing the parameters appropriately, for example, the appropriate choice of detuning allows us to increase the maximum entropy of the system, which was ∼ 0.45 in Fig. 6(c) and passed to be ∼ 0.75 in Fig. 7(c), another example can be seen in the excitation inversion that no longer occurs Figs. 11(b) and 11(c) and conversely occur in Figs. 12(b) and 12(c).

In summary, it was shown that, when using the intensity-dependent BS model extended to a realistic scenario taking into account influence of losses, detuning and time dependent external fields, interesting results emerge. This also indicates that one can perform a dynamic control of subsystem properties through the manipulation of parameters involved, with potential applications to the command of quantum information processes. We have also shown that the decoherence effect is greater in the CQED, which is due to the fact that the CQED can have more excitations than the CPB. Decoherence affecting the CQED can be reduced by improving its quality. We hope that these results could provide some good insights for researchers in this area.

Reference
[1] Xiang Z. L. Ashhab S. You J. Q. Nori F. Rev. Mod. Phys. 85 2013 623
[2] Jiang C. Cui Y. S. Liu H. X. et al. Chin. Phys. B 24 2015 54206
[3] Duty T. Physics (College. Park. Md). 3 2010 80
[4] Guo Q. Cheng L. Y. Wang H. F. Zhang S. Chin. Phys. B 24 2015 40303
[5] Buluta I. Ashhab S. Nori F. Rep. Prog. Phys. 74 2011 104401
[6] Morton J. J. L. Lovett B. W. Annu. Rev. Condens. Matter Phys. 2 2011 189
[7] Valverde C. Castro A. N. Baseia B. Opt. Commun. 366 2016 301
[8] Yan R. Y. Wang H. L. Feng Z. B. Int. J. Theor. Phys. 55 2016 258
[9] Petersson K. D. McFaul L. W. Schroer M. D. et al. Nature (London) 490 2012 380
[10] Girvin S. M. Devoret M. H. Schoelkopf R. J. Phys. Scr. T 137 2009 014012
[11] Feng Zhi-Bo Li M. Physica C 507 2014 65
[12] Devoret M. H. Girvin S. Schoelkopf R. Annalen der Physik 16 2007 767
[13] Devoret M. H. Schoelkopf R. Science 339 2013 1169
[14] Kippenberg T. J. Vahala K. J. Science 321 2008 1172
[15] Kippenberg T. J. Vahala K. J. Opt. Express 15 2007 17172
[16] Ivan F. Khaled K. Nature Photonics 3 2009 201
[17] Aspelmeyer M. Kippenberg T. J. Marquardt F. Rev. Mod. Phys. 86 2014 1391
[18] Brennecke F. Ritter S. Donner T. Esslinger T. Science 322 2008 235
[19] Rabl P. Phys. Rev. Lett. 107 2011 063601
[20] Liao J. Q. Nori F. Phys. Rev. A 88 2013 023853
[21] Gustafsson M. V. et al. Science 346 2014 207
[22] Schreier J. A. et al. Phys. Rev. B 77 2008 180502
[23] Purdy T. P. et al. Phys. Rev. Lett. 105 2010 133602
[24] Wezel J. V. Oosterkamp T. H. Proc. R. Soc. A 468 2012 35
[25] Lü X. Y. Xiang Z. L. Cui W. et al. Phys. Rev. A 88 2013 12329
[26] Jöckel A. et al. Nature Nanotechnology 10 2014 55
[27] Pflanzer A. C. Romero-Isart O. Cirac J. I. Phys. Rev. A 88 2013 033804
[28] Pirkkalainen J. M. et al. Nature (London) 494 2013 211
[29] Pirkkalainen J. M. Cho S. U. Massel F. et al. Nature Communications 6 2015 6981
[30] Janowicz M. Phys. Rev. A 57 1998 4784
[31] Fei J. S. Y. X. Yang Y. P. Chin. Phys. B 18 2009 3193
[32] Li J. J. Zhu K. D. Appl. Phys. Lett. 94 2009 63116
[33] Li J. J. Zhu K. D. Appl. Phys. Lett. 94 2009 249903
[34] Buck B. Sukumar C. V. Phys. Lett. A 81 1981 132
[35] Schoelkopf R. J. Girvin S. M. Nature (London) 451 2008 664
[36] Blais A. Huang R. S. Wallraff A. et al. Phys. Rev. A 69 2004 062320
[37] Chen Y. L. Xiao Y. F. Zhou X. et al. J. Phys. B: At. Mol. Opt. Phys. 41 2008 175503
[38] Eberly J. H. Narozhni J. B. Sanchez-Mandragon J. J. Phys. Rev. Lett. 44 1980 1323
[39] Rodrígues-Lara B. M. J. Opt. Soc. Am. B 31 2014 1719
[40] Rodríguez-Lara B. M. Soto-Eguibar F. Cárdenas A. Z. Moya-Cessa H. M. Opt. Express 21 2013 12888
[41] Chaba A. N. Baseia B. Wang C. X. Vyas Recta Physica A 232 1996 273
[42] Valverde C. Baseia B. Mod. Phys. Lett. B 32 2018 1850026
[43] Koch J. Yu T. M. Gambetta J. et al. Phys. Rev. A 76 2007 042319
[44] Fink J. M. Bianchetti R. Baur M. et al. Phys. Rev. Lett. 103 2009 083601
[45] Phoenix S. J. D. Knight P. L. Phys. Rev. A 44 1991 6023
[46] Einstein A. Podolsky B. Rosen N. Phys. Rev. 47 1935 777
[47] Brune M. Hagley E. Dreyer J. et al. Phys. Rev. Lett. 77 1996 4887
[48] Monroe C. Meekhof D. M. King B. E. Wineland D. J. Science 272 1996 1131