† Corresponding author. E-mail:
In this paper we present a general theoretical model for the interaction between a number of two-level atoms constituting Bose-Einstein condensate (BEC) and a single-mode quantized field. In addition to the usual interacting terms, we take into account interatom as well as higher-order atom-field interactions. To simplify the Hamiltonian of system, after using the Bogoliubov approximation we proceed to calculate the transformed operators of atoms and field. Then, to quantify the spontaneous emission, we get analytical expressions for the expectation value of 
The interaction between atomic dipole moments and the vacuum state of a quantized field leads to spontaneous emission (SE). Experimental results show that the SE from excited atoms can be either enhanced or suppressed.[1–2] The recent progress of Bose-Einstein condensate (BEC) in magnetic traps has created a new state of matter where all atoms share a single macroscopic quantum state.[3] This leads to great opportunities to explore and test new phenomena related to macroscopic quantum coherence. In recent years authors have theoretically studied SE in a trapped BEC. In this respect, the continuous center-of-mass momentum distribution leads to an increase of SE.[4–5] In this line of research, different physical aspects and various usefulness of BEC systems have been recently considered and discussed.[6–9] It should be noted that, the dynamics of BEC systems and their corresponding interesting topics have been mostly investigated, as a few one may refer to the interference effects between two BECs,[10] superfluidity and coherence in BECs[11] and many of fundamental challenging papers have been published elsewhere.[12] The process of collective SE in the Dicke model has been investigated in the literature. An exact solution for the SE of a multi-photon single-atom Dicke model has been obtained.[13] Also, the SE in the presence of N atoms was analytically presented for the case in which only one atom is initially excited.[14–15] The collective SE from a system of two atoms with multi-photon transitions in a cavity has been studied in Ref. [16]. Collective SE from a BEC in the framework of a multi-photon q-deformed Dicke model has been investigated in Ref. [17] The effect of atomic collisions on the collective spontaneous emission from an f-deformed BEC has been studied.[18] Lately, controlling SE noise in measurement-based feedback cooling of a BEC has been reported.[19] A general theoretical model of the interaction between a single-mode cavity field and the excitons, which leads to collapses and revivals of exciton emission in a semiconductor microcavity has been presented.[20] Recently, we investigated the quantum dynamics of a system consisting of atomic BEC and a single-mode quantized field in the presence of interatom collisions, which leads to clear collapse-revival (CR) phenomenon specially in the atomic population inversion.[21–22]
In the present paper we first give a general theoretical model of the interaction between a single-mode cavity field and a BEC system consisting of N two-level atoms in the presence of interatom collisions and higher-order (nonlinear) interaction of photons, where the atoms are in their excited states. We consider the vacuum state as the initial state of field, therefore, we are able to evaluate the SE in our considered system. Then, to quantify the SE, the expectation values of 
This paper is organized as follows. In the next section, the model and the analytical equations of transformed operators of field and atoms are presented. In Sec. 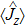
According to the experimental results of Mewes et al. in 1997,[23] short pulses of rf radiation can be used to create a BEC in a superposition of trapped and untrapped states. In this respect, we consider a system, which consists of a BEC of N two-level atoms in a magnetic trap coupled to an rf field. In fact, the atomic subsystem is a BEC consisting of N atoms with two internal state (|1⟩, |2⟩) in a magnetic trap, which coupled to a single-mode rf field. The second quantization of the Hamiltonian model is given by
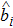
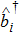
In order to study the dynamical properties of the system, we use Bogoliubov approximation, in which the slow change of the atom number in the ground state can be neglected in the process of interacting with quantized field when the number of BEC atoms at initial moment is enough large. Therefore, one can replace the ground state operators of BEC with a c-number 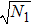
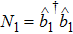
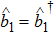
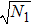
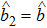
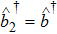
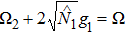
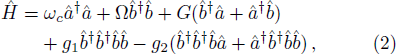
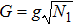
The first-order interaction between the atom and the field is described by the linear operators of atom and field,[30] therefore, the term contains the nonlinear operators may be referred to as higher-order interaction term. Also, the higher-order atom-field interaction represents the phase-space filling effects as is mentioned in Ref. [31]. It should be noticed that, we have neglected a constant term, which contains the average number of the condensate atoms in the state |1⟩ (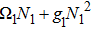
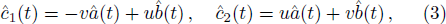
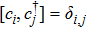
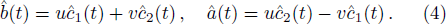
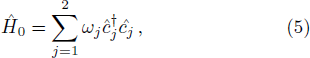
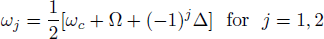
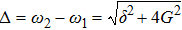
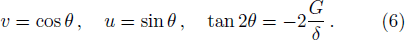
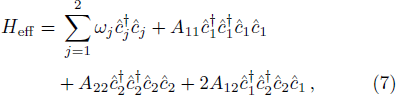
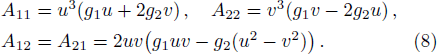
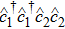
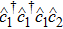
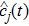
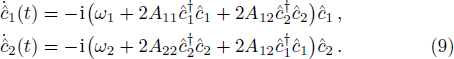
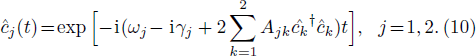
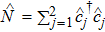
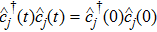
To achieve the time variation of API, we introduce the Schwinger angular momentum operators as
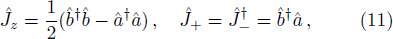
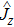
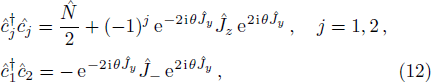
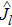
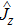
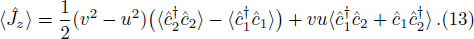
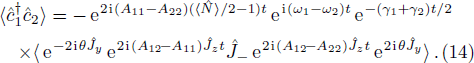
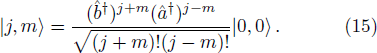
The spontaneous emission (SE) arises from the interaction between atomic dipole moments and the vacuum of the radiation field. To evaluate this quantity, we proceed to investigate the API as a measure for the rate of SE in our considered BEC atomic system. Since, we have represented the BEC operators in terms of the angular momentum operators, therefore, we define API as the expectation value of 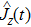
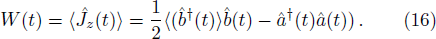
The initial state vector of the system, which is the direct product of the two initial BEC and field states can be written in terms of the eigenstates of 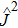
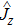
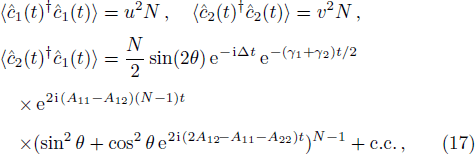
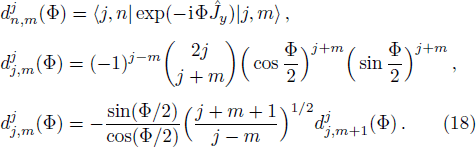
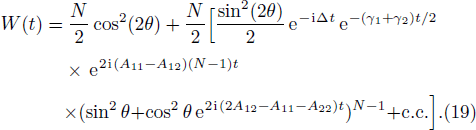
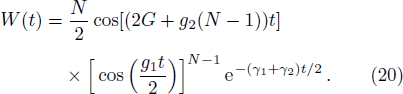
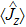
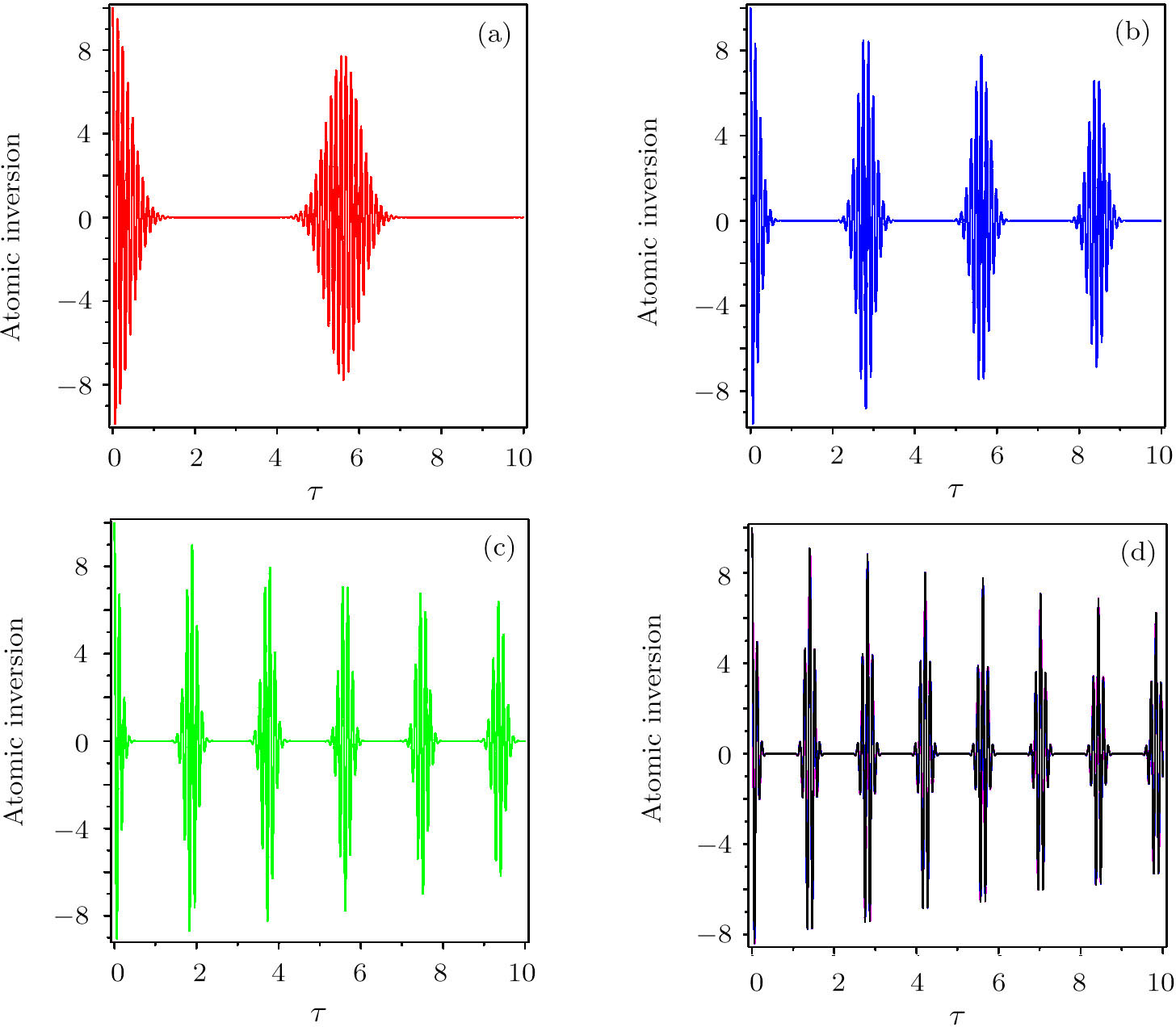
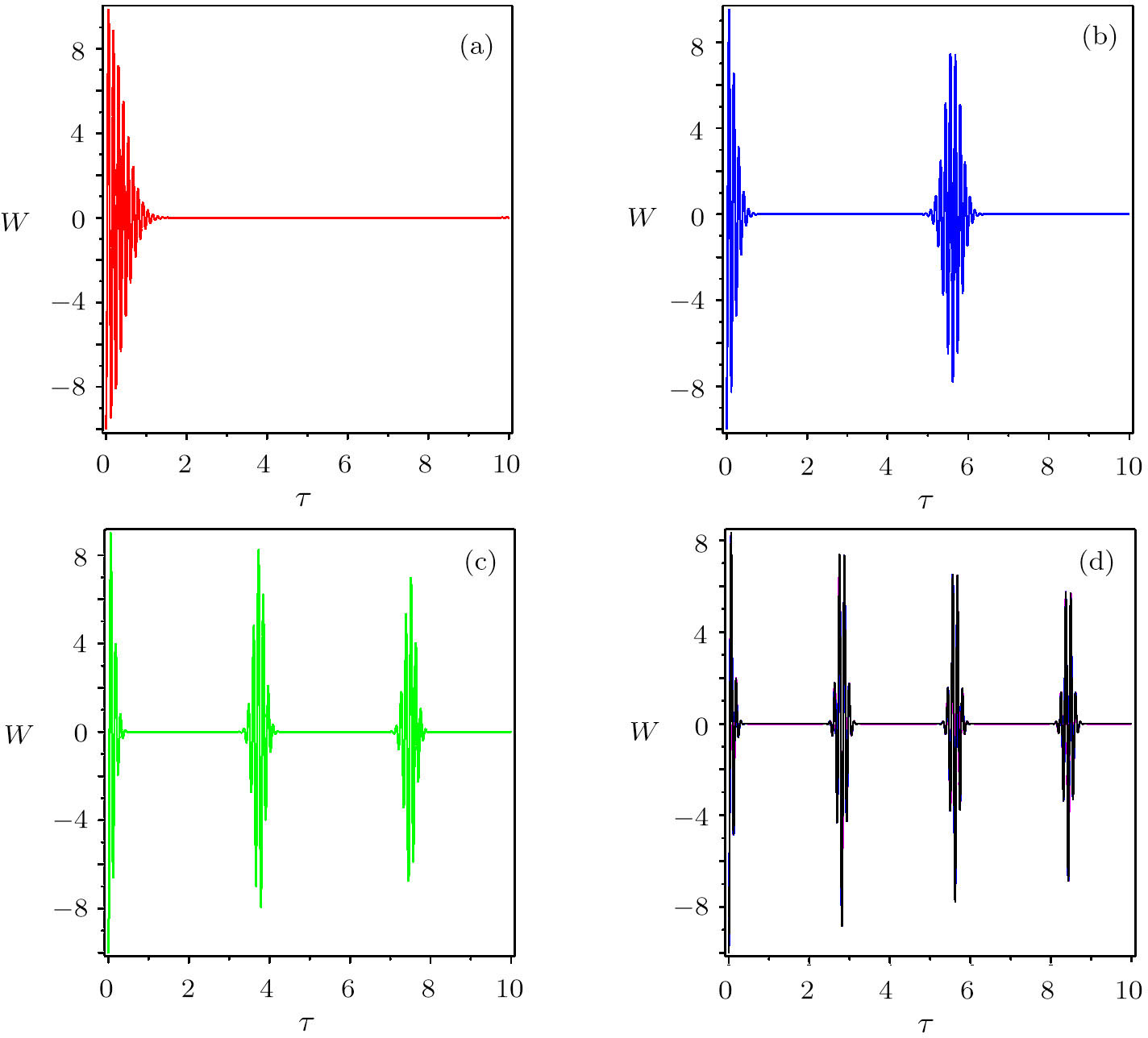
 | Fig. 1 The evolution of API for γ1 = γ2 = 0.01G, g1 = g2 = 0.5G against the dimensionless time τ = gt in the resonance regime. (a) N = 10, (b) N = 20, (c) N = 50, (d) N = 100. |
Figure 
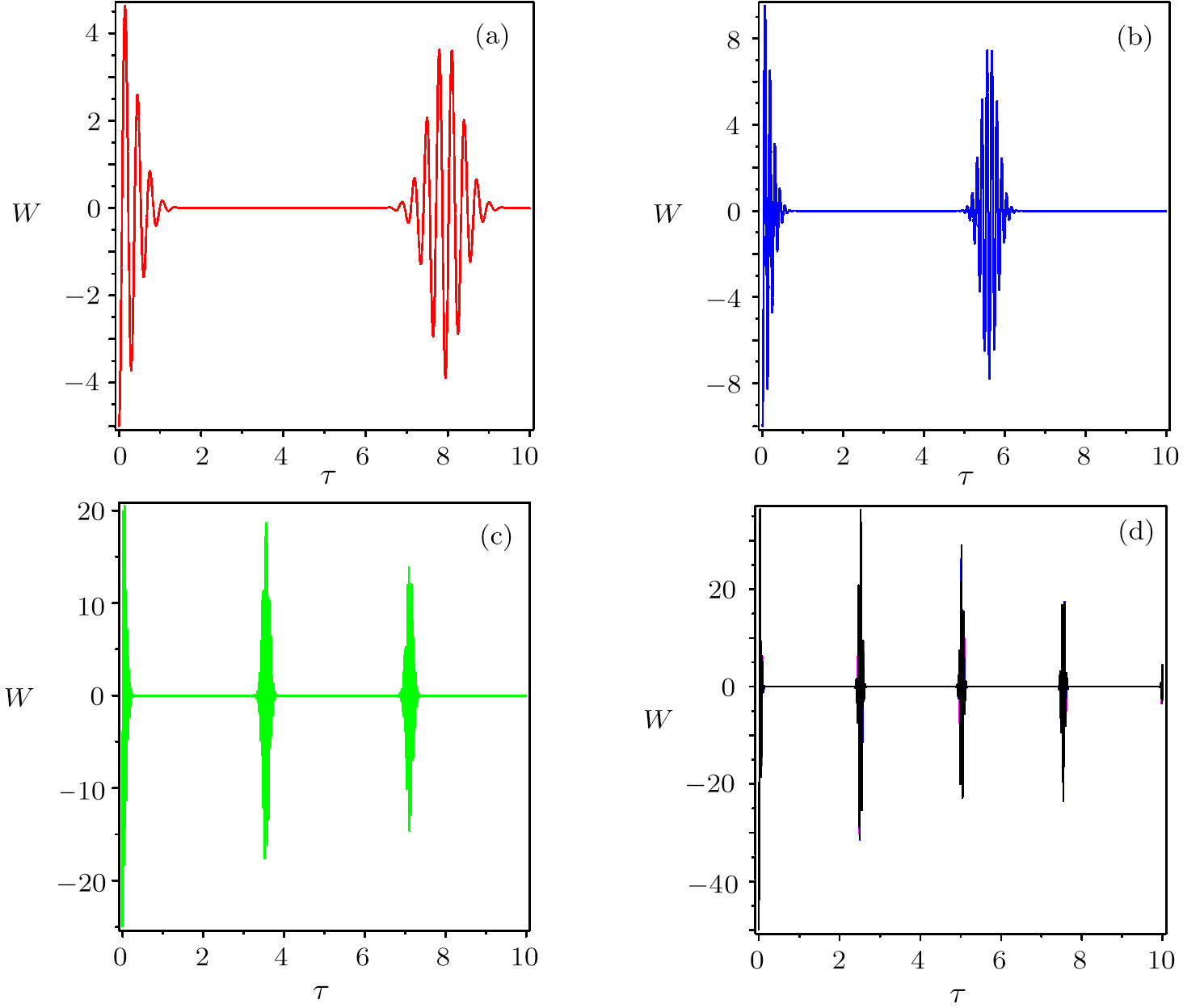
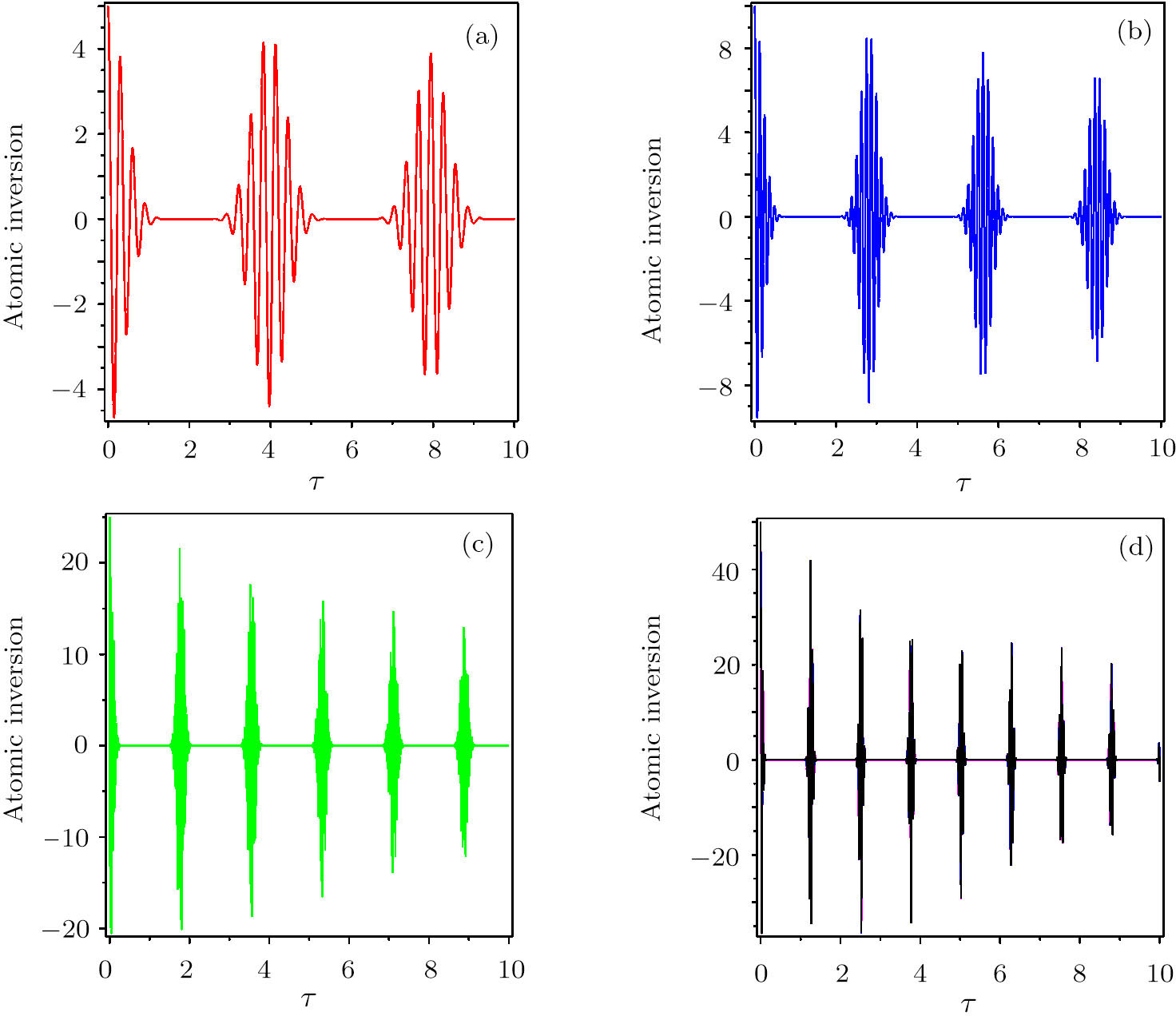
 | Fig. 2 The influence of dissipation on the time evolution of API for N = 20 and g1 = g2 = 0.5G in the resonance regime. (a) γ1 = γ2 = 0.0, (b) γ1 = γ2 = 0.01G, (c) γ1 = γ2 = 0.1G, (d) γ1 = γ2 = 1.0G. |
To achieve more insights into the effect of initial state of BEC atoms on the API, we consider another initial state for the system. In this respect, we assume that at t = 0 the cavity field is in the ground state and the BEC atoms are in the coherent state. Consequently, the initial state of the total system reads as
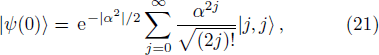
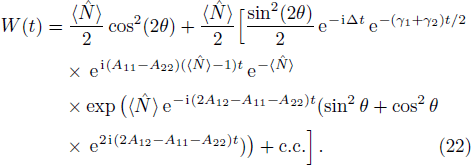
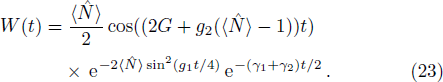
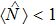
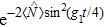
The revival periods of oscillation in the coherent state may be determined as 4π/g1. Also, we found that increasing the interatoms interaction strength in the coherent state case leads to an increment in the number of revivals in a fixed interval of time, but does not significantly affect the amplitude of API (Fig. 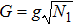
 | Fig. 5 The effect of interatoms interaction on the time evolution of API for N = 20, γ1 = γ2 = 0.01G and g2 = 0.5 G in the resonance regime. (a) g1 = 0.25G, (b) g1 = 0.5G, (c) g1 = 0.75G, (d) g1 = G. |
The observation of CRs in nonlinear systems such as the nonlinear directional coupler,[35] the relative phase between two superfluids or superconductors,[36] exciton-exciton interaction in a semiconductor microcavity,[32] and the population imbalance of a two-mode BEC[37–40] have been investigated. In this line of research we also showed that the nonlinear interactions in the our presented model can lead to CR phenomenon.
Summing up, we outlined a theoretical model for the investigation of quantum dynamic of BEC interacting with a single-mode quantized field in the presence of interatom collisions and higher order atom-field interaction terms. In this line and to achieve the purpose of paper, at first, via solving the equation of motion the transformed operators of system have been analytically obtained. In the continuation, the API (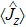
We briefly present our concluding remarks in what follows:
Number of atoms: by fixing all parameters except the number of atoms in BEC, it is found that increasing the number of BEC atoms leads to the occurrence of more revivals in a definite interval of time, so apparently the intervals of collapse time are considerably decreased. Interatomic coupling constant: the occurrence of CR phenomenon in the temporal behaviour of API strongly depends on the interatomic coupling constant. In detail, by tuning the latter parameter, one can control the number of CRs in a fixed interval of time. Initial BEC state: it is shown that the time evolutions of both SE or API in the number state and the coherent state as initial states are quite different. In particular, in the number state (coherent state) the revival periods of oscillations read as 2π/g1 (4π/g1). The critical requirement of the CRs is the interatom interactions. The behavior of CRs can be controlled by changing the interatom interaction constant (parameter g1). In the weak nonlinearity condition (Ng2 ≪ G), in both coherent and number states the period of oscillations can be adjusted by tuning the number of atoms in BEC and the atom-field coupling constant Damping effect: the damping parameter lowers the amplitude of revivals, and change the time of CRs. Indeed, in the weak decay regime there is no considerable change in the CRs time, however, the decaying of amplitude is clearly visible (comparing Figs.
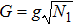
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] |