Extensive studies have appeared to investigate the particle velocity anisotropy and relaxation mechanism during the last few decades in space plasmas.^[1–2] It has been observed that the distribution function of particles becomes anisotropic in a magnetized and collisionless plasma. Such anisotropic effects in space plasmas are responsible for processes like wave instabilities and magnetic expansion or compression.^[1–2] These plasma instabilities produced by the temperature anisotropy may grow either in perpendicular or parallel direction (with respect to the ambient magnetic field).^[3] If the wave-vector is perpendicular to the ambient magnetic field B₀ (i.e., k⊥B₀), the driver of the instability along the ambient magnetic field must exceed the perpendicular kinetic energy of plasma particles such as in temperature anisotropy, T_‖ > T_⊥, or a streaming beam of plasma particles (v_b ‖ B₀). These conditions frequently occur in the solar wind.^[3–4] According to both theory and observation, a well known characteristic of solar wind plasma is the presence of an anisotropic velocity distribution function.^[5–11]

The ordinary wave (ordinary mode) is a high frequency, linearly polarized, perpendicularly propagating (k ⊥ B₀ and E₁ ‖ B₀) electromagnetic wave. Due to a large number of applications in space plasmas the ordinary mode instability has received special attention,^{[3–4,7,12–16]} and the mode has been studied both in classical and degenerate plasmas.^{[3–4,7,12–18]} For instance, Davidson and Wu discussed the ordinary mode instability for a high beta plasma and observed that the mode becomes unstable for T_‖ > T_⊥ in a high beta plasma.^[19] Nambu investigated the dispersion relation of the ordinary mode by considering non-uniformities of magnetic field (▽B), density (▽ N), and temperature (▽ T). It was noticed that in an inhomogeneous plasma the ordinary mode becomes unstable under the condition T_⊥ > T_‖, in contrast to the previous results i.e., T_‖ > T_⊥.^[20] Bornatici et al., investigated the ordinary mode instability for counter streaming electron plasma with temperature anisotropy. It was noticed that the perpendicular temperature stablizes whereas the parallel temperature enhances the instability.^[21] Recently, the ordinary mode instability has been discussed both numerically and analytically by taking different limits of the plasma beta and temperature anisotropy.^{[3–4,7,12–16]}

In space and laboratory plasmas, energetic particles are present that result in long-tailed distributions. These distributions show deviations from the Maxwellian equilibrium and may exist in low-density plasma in the Universe, where collisions between charged particles are quite rare.^[3,8,22] In order to model these high energy tails (energetic particles) with excess of energetic particles, Cairns et al., introduced a distribution function (observed in space plasmas) which is given as

Fig. 1

	Figure Option ViewDownloadNew Window
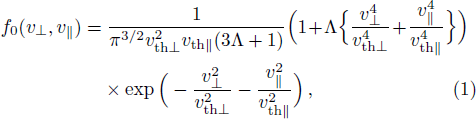
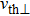
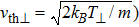
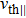
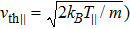
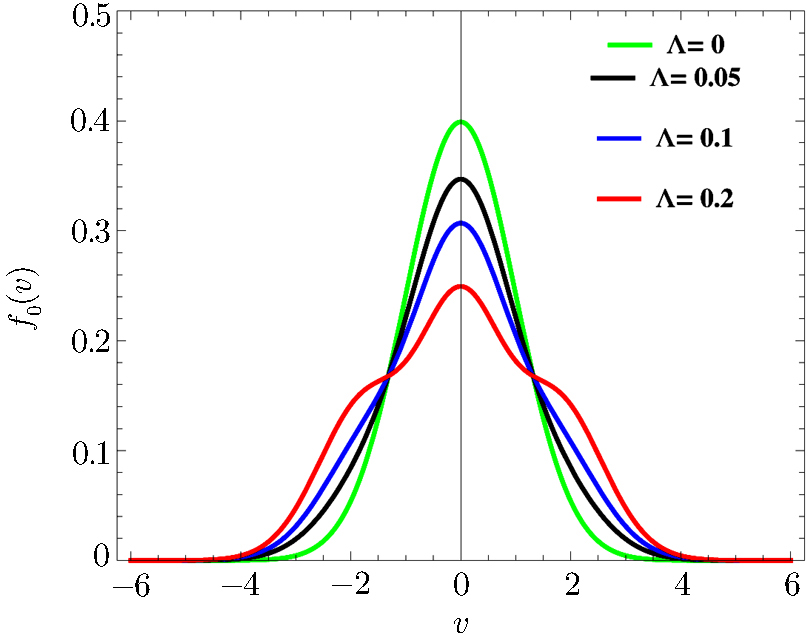	Fig. 1 (Color online) Plot of normalized Cairns distribution function against v for different values of Λ.

From the above literature, one may notice that the electromagnetic wave instabilities driven by electron temperature anisotropy have been well studied for the bi-Maxwellian distributed space plasma environments. Therefore, it is very interesting to examine the effect of nonthermal electrons on the dispersive properties of electromagnetic wave instabilities. To the best of our knowledge, the wave instabilities induced due to the temperature anisotropy such that T_‖ > T_⊥ in a Cairns distributed plasmas is not yet explored. In the present work we focus on that and examine the ordinary mode instability in the presence of temperature anisotropy (T_‖ > T_⊥) as well as high energy tails in the space plasma environments like solar wind.

The plan of the present paper is as follows: In Sec. 2, we present the mathematical formalism to investigate the dispersion relation of the ordinary mode in a Cairns distributed electron plasma. In Sec. 3, we present the instability analysis of the mode and give graphical analysis of the dispersion relations. Finally, in Sec. 4 we present a summary of the manuscript.

In order to study the dispersion characteristics of the ordinary mode we consider a collisionless electron-ion plasma embedded in an external magnetic field, described by a set of Vlasov-Maxwell equations:

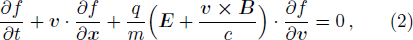
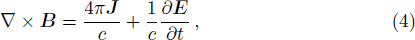
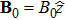
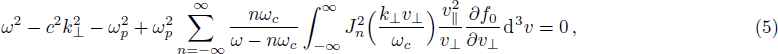
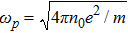
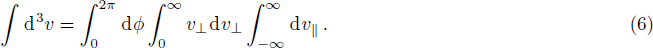
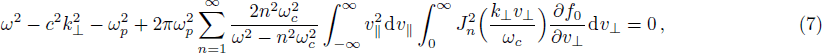
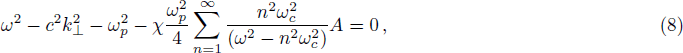
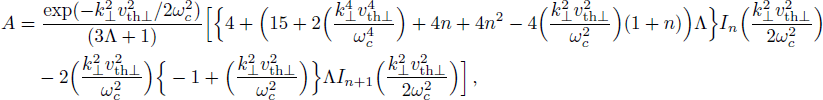
In the spectrum of perpendicularly propagating modes, it has been observed that only the ordinary mode is affected by the temperature anisotropy. In order to study the growth rate of the ordinary mode we restrict ourselves to n = 1. Therefore the Eq. (8) reduces to

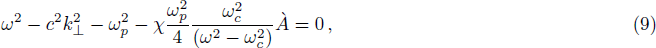
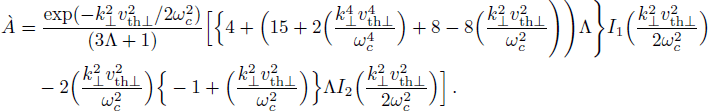
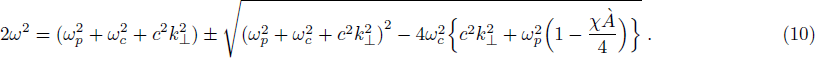
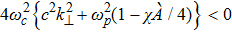
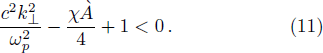
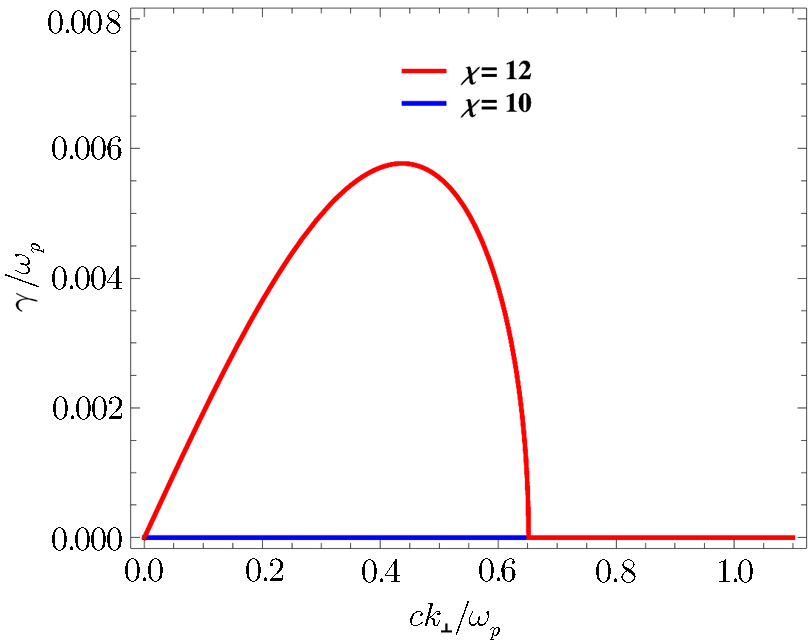
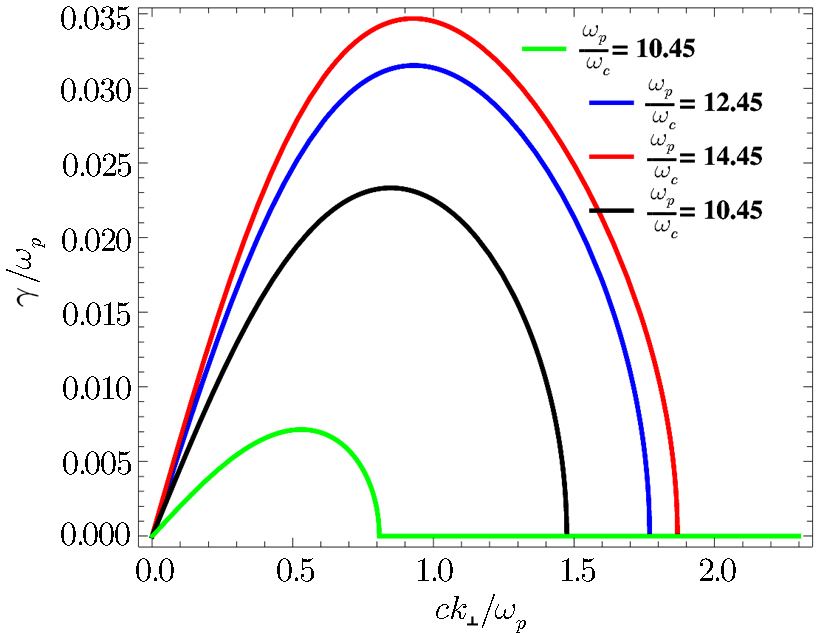
For the choice of parameters n₀ = 10⁹ cm⁻³, B₀ = 10 G, Λ = 0.2 and v_th⊥/c = 0.05, it is found that the instability starts from χ ≥ 12 as shown in Fig. 2. However, if we increase the values of density from 10⁹ cm⁻³ to 5 × 10⁹ cm⁻³ the instability starts even at lower values i.e., at χ = 5 as shown in Fig. 3. Thus we can say that for a low density region large values of temperature anisotropy are required to make the mode unstable but instead in the high density region even smaller values of anisotropy can excite the mode.

Fig. 2

	Figure Option ViewDownloadNew Window
	Fig. 2 (Color online) Effect of temperature anisotropy on the growth rate of the ordinary mode (with fixed value of density, ambient magnetic field and non thermality parameter i.e., n0 = 109 cm−3 and B0 = 10 Gauss, Λ = 0.1).

Fig. 3

	Figure Option ViewDownloadNew Window
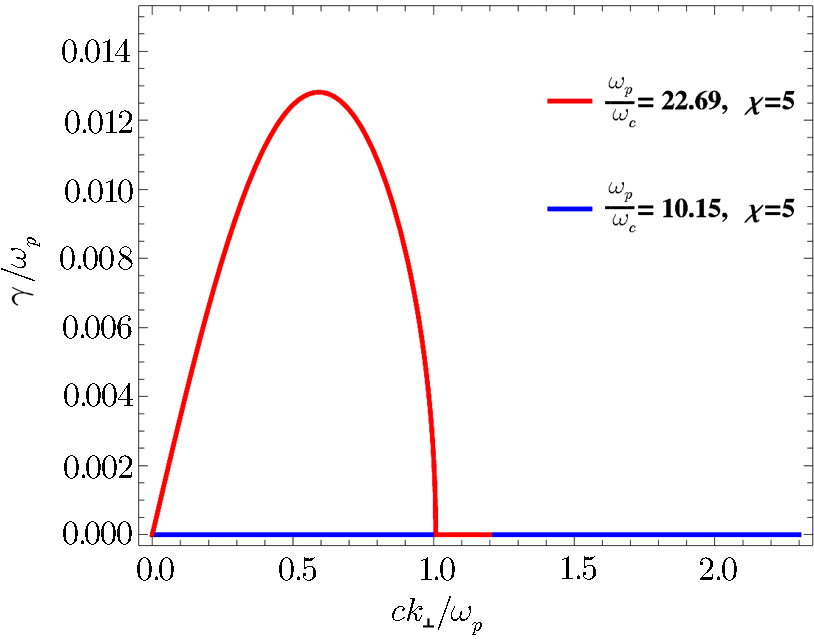	Fig. 3 (Color online) Effect of temperature anisotropy on the growth rate of the ordinary mode (with fixed value of ambient magnetic field and non thermality parameter i.e., B0 = 10 Gauss, Λ = 0.2.)

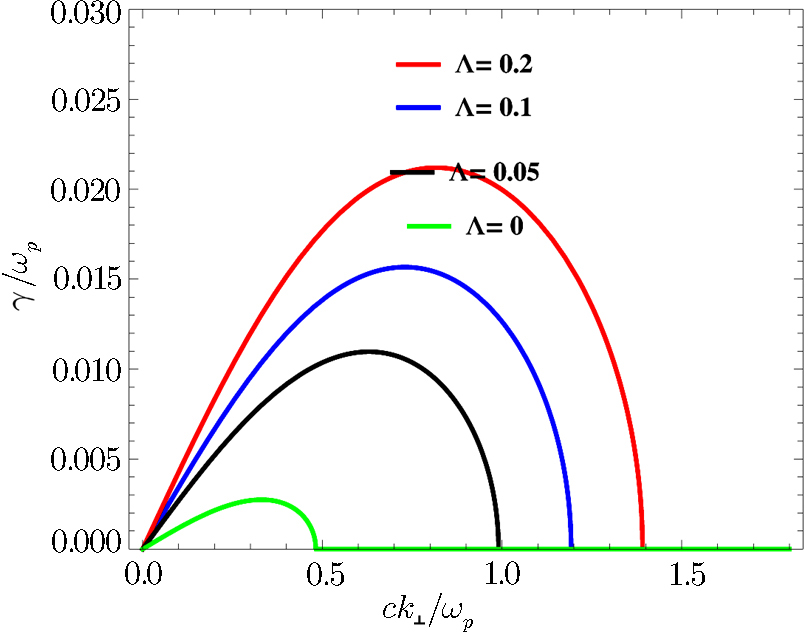
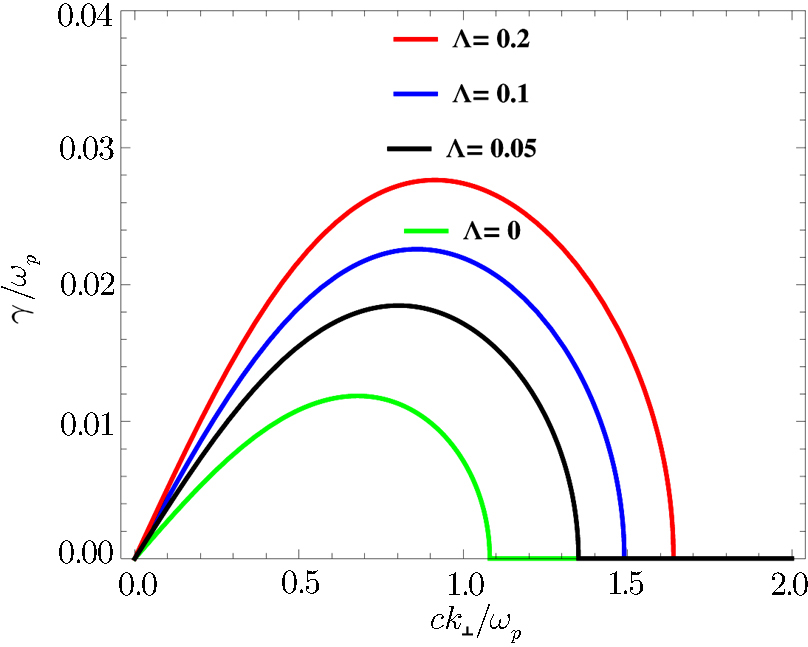
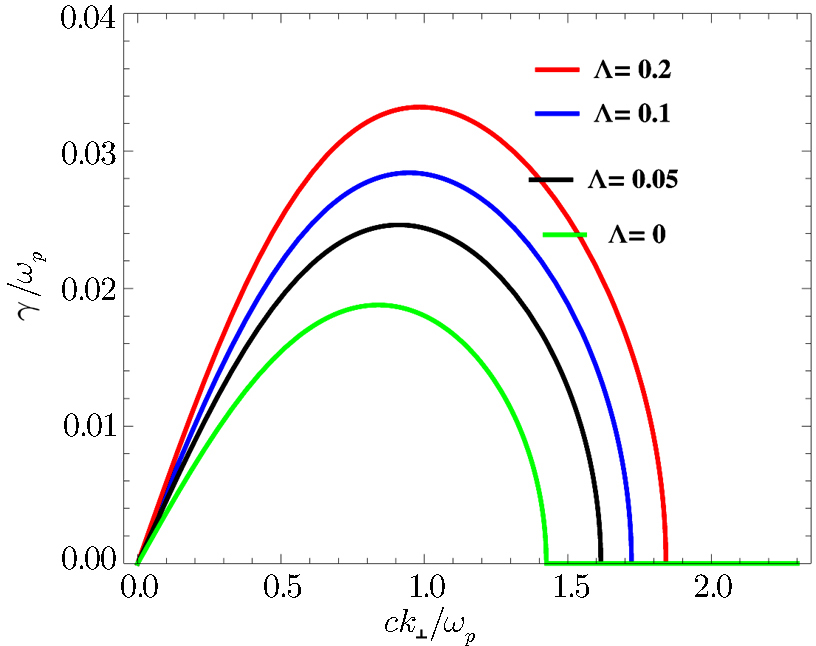
Further, a comparison of Figs. 4 and 5 shows that at fixed values of temperature anisotropy for instance, χ = 20, the maximum value of growth rate for Λ = 0.1 is 0.028 whereas for Λ = 0.2, the maximum growth rate is 0.032, which means that the growth rate has been increased 4 times due to an excess of energetic particles. The green line shows Maxwellian result i.e., Λ = 0, the value of temperature anisotropy that we have used for Maxwellian case is χ = 18.

Fig. 4

	Figure Option ViewDownloadNew Window
	Fig. 4 (Color online) Effect of variation of non thermality parameter on the ordinary mode instability (with fixed value of density, ambient magnetic field and temperature anisotropy i.e., n0 = 109 cm−3 and B0 = 10 Gauss, χ = 16). The green line is for Maxwellian distribution wherein Λ = 0.

Fig. 5

	Figure Option ViewDownloadNew Window
	Fig. 5 (Color online) Effect of variation of non thermality parameter on the ordinary mode instability (with fixed value of density, ambient magnetic field and temperature anisotropy i.e., n0 = 109 cm−3 and B0 = 10 Gauss, χ = 18). The green line is for Maxwellian distribution wherein Λ = 0.

From Figs. 4 and 5 it can be seen that the growth rate in the Cairns distributed plasma is larger than in the Maxwellian plasma which means that the presence of energetic particles support the anisotropy to enhance the growth rate of instability. Figure 6 shows that the effect of non-thermality parameter Λ on the growth rate of the instability. It can be seen that by increasing the number of energetic electrons (Λ), the growth rate is increased and the instability is extended to large wave numbers. Because due to excess of energetic electrons, the wave will get more energy from the system. Figure 7 shows how the equilibrium number density (n₀) affects the growth rate of the instability i.e., with the increase in n₀, the magnitude of the growth rate and k-domain is increased.

Fig. 6

	Figure Option ViewDownloadNew Window
	Fig. 6 (Color online) Effect of variation of non thermality parameter on the ordinary mode instability (with fixed value of density, ambient magnetic field and temperature anisotropy i.e., n0 = 109 cm−3 and B0 = 10 Gauss, χ = 20). The green line is for Maxwellian distribution wherein Λ = 0.

Fig. 7

	Figure Option ViewDownloadNew Window
	Fig. 7 (Color online) Effect of density variation on the ordinary mode instability (with fixed value of ambient magnetic field and temperature anisotropy χ = 20). The green line is for Maxwellian distribution wherein Λ = 0.

Using the linearized Vlasov-Maxwell equations, we have derived the generalized dispersion relation for the ordinary mode alongwith the instability and threshold condition in the Cairns distributed plasma. In the instability analysis we find that in the low density region the larger values of anisotropy are required to excite the ordinary mode instability whereas in the high density regimes even smaller values of anisotropy can excite the mode. Further, we have investigated the effects of the population of the energetic electrons (Λ), equilibrium number density (n₀) and temperature ratio (χ) on the growth rate of the ordinary mode instability. The parameter Λ supports temperature anisotropic factor χ to enhance the growth rate of the instability. We have also found that all these parameters enhance the growth rate and enlarge the domain of the wave number. Moreover, we have also found that the growth rate of the ordinary mode instability is greater for the Cairns distributed electrons as compared to their Maxwellian counterparts. So, our findings may be helpful to explain the mechanism of waves and instabilities in the space plasma environments, where one comes across velocity distributions of such types.