According to the so-called cosmic censorship conjecture,^[1] all physical singularities due to gravitational collapse should be hidden behind an event horizon. This hypothesis that no naked singularity occurs in our universe can be described in weak and strong versions.^[2] One way of testing the week cosmic censorship conjecture (WCCC) is to throw a test particle into an existing black hole. If the particle can pass through the horizon and change the parameters of the black hole so that the horizon disappears, then the cosmic censorship conjecture might break down.

The seminal work was done by Wald,^[3] which showed that a test particle can not destroy the horizon of an extremal Kerr-Newman black hole. From then on, many authors followed the spirit of Wald’s gadanken experiment and revisited the problem of WCC violation. Some of the attempts involving test particles have been successful to produce naked singularities.^[4–8] For example, Jacobson et al.^[4] asserted that it would be possible to destroy a Kerr black hole with infalling test particle if we start with a near-extremal configuration, rather than an extremal black hole. In Ref. [5], Hubeny showed that overcharging a near-extremal Reissner-Nordstrom (RN) black hole is possible by injecting a test particle into the black hole. For charged and spinning black holes, it is possible to destroy an extremal^[9] and near-extremal^[10] Kerr-Newman black hole by a test particle with electric charge and angular momentum by neglecting the backreaction effect. The issue about the problem of cosmic censorship has been extensively studied in recent years.^[11–19]

Since the discovery of the AdS/CFT correspondence,^[20–22] its developments have brought about many new insights into the nature of black holes. The study of asymptotically anti-de Sitter black holes has become more important and realistic than ever. It is interesting to know the role of Λ in the discussing turning a black hole into a naked singularity by plugging a test particle into black hole. Recently, Zhang et al.^[23] asserted that an extremal Reissner-Nordström anti-de Sitter black hole can be overcharged by a test particle and both extremal Kerrde-Sitter/anti-de-Sitter black holes can be overspun by a test particle, which implies a possible breakdown of the cosmic censorship conjecture. Moreover, we have also recovered that a test particle may destroy the horizon of an extremal Kerr-Newman-AdS black hole, resulting in an apparent violation of the cosmic censorship.^[24] In this paper, we further study the near-extremal Kerr-Newman-AdS black holes, and will find that the possibility to destroy a near-extremal Kerr-Newman-AdS by plunging test particles across their event horizon when neglecting the self-force, self-energy, and radiative effects. We also provide a numerical plot showing that a test particle, which potentially could destroy the black hole, could really fall all the way from infinity into the black hole.

In Sec. 2 we show how a near-extremal Kerr-Newman-AdS black hole can be destroyed by plunging test particle across its event horizon. Finally in Sec. 3, we give a closing remarks. In this paper we use the unit system where c = G = ħ = 1.

In four-dimensional spacetime, the Kerr-Newman-AdS metric takes the following form in Boyer-Lindquist-type coordinates^[24–25]

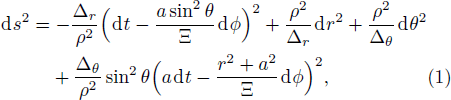
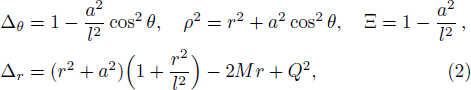
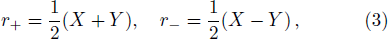
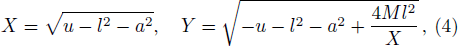
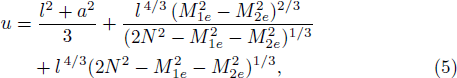
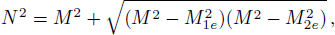
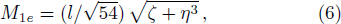
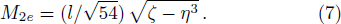
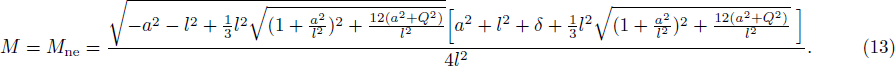
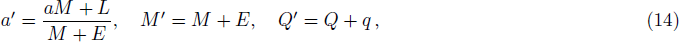
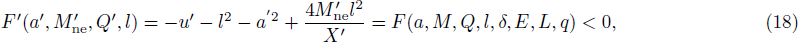
Now let us consider a test particle with electric charge q, energy E, and orbital angular L moves along a geodesic in a Kerr-Newman-AdS spacetime, the conserved energy of the test particle is described as^[24,27]

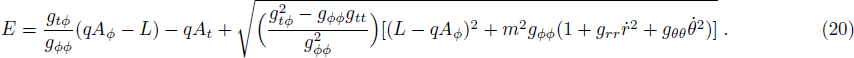
To investigate the range of energy ΔE, we chose the parameters Q = 23.217 58, a = 0.1, q = 0.1, L = 0.1, then the radius of extremal black hole is 3.638 34 and mass M is 100. By choosing the values of δ, we can get the corresponding values of E_max by solving Eq. (18), so one can get a set of values [δ, E_max] for plotting the curve of δ-E_max, which we provide in Fig. 1(b).

Fig. 1

	Figure Option ViewDownloadNew Window
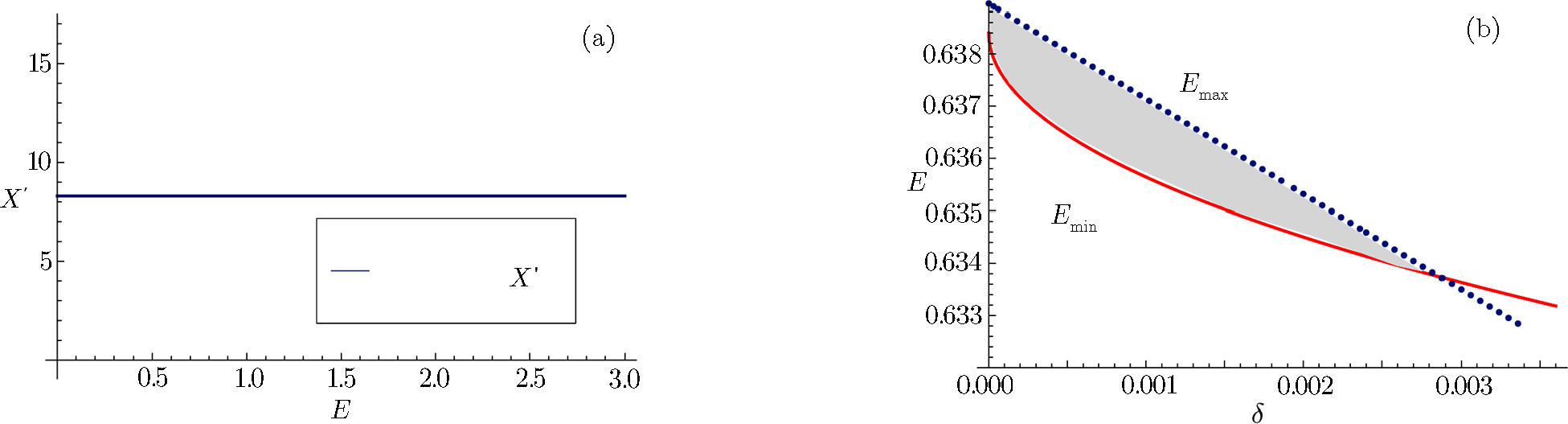	Fig. 1 (a) Plot of E-X′. X ≥ 0 assure the extremal condition of black hole we used as a judgment is meaningful. (b) Plot of E-δ. the shadow area is E ˂ Emax and E ˃ Emin.

In order to get the minimum energy for the particle to reach the event horizon, we can rewrite Eq. (12) as

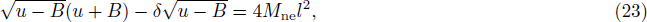
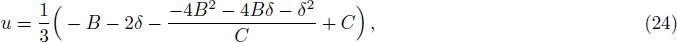
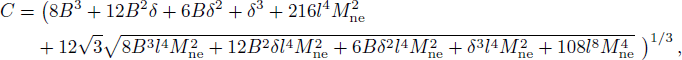
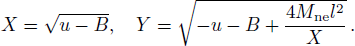
Based on Eqs. (21), (24), (25), by using the same parameters Q = 23.217 58, a = 0.1, q = 0.1, L = 0.1 as mentioned above, we can plot the curve of δ-E_min which we show in Fig. 1(b). To prove Eq. (19) is satisfied, using the same numerical values with δ chosen to be 0.004, we provide Fig. 1(a).

From Eq. (24), we can see the value of function u will decrease as δ increases, so if δ takes values in [0, 0.004], δ is chosen to be 0.004 will give the minimum value of X. From Fig. 1(a), we can see when particle’s energy E ranges from 0 to 3, the condition Eq. (19) is always satisfied. Figure 1(b) shows ΔE gets narrower as δ increases, this implies that the black hole is harder to destroy when it moved from the extremality. We can see there is a narrow range of the test particle’s energy, ΔE, which allows the appearance of naked singularity from both the near-extremal and extremal Kerr-Newman-AdS black hole. For extremal case (δ = 0), we get 0.638 402 ˂ E ˂ 0.638 955 and ΔE = 0.000 553. For illustration, we take δ = 0.001 and find 0.635 641 ˂ E ˂ 0.637 13, so ΔE = 0.001 489. We choose E = 0.636, which is just between E_max and E_min. By using the same numerical values as those in obtaining Fig. 1(b), we get the plot of Δ′-r in Fig. 2(a).

Fig. 2

	Figure Option ViewDownloadNew Window
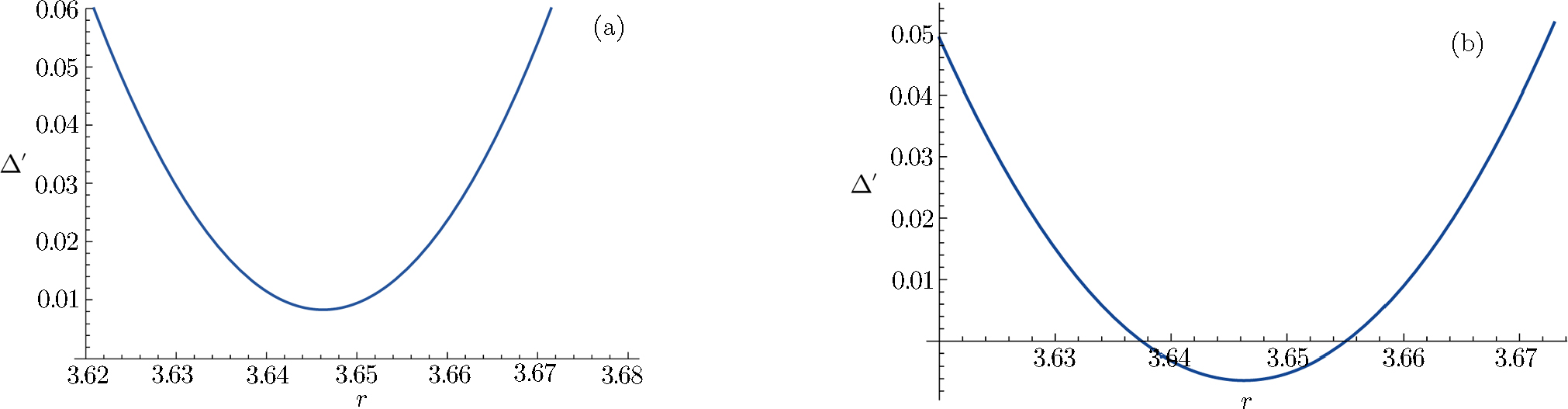	Fig. 2 Plot of Δ′-r after capturing a test particle. (a) Plot of Δ′-r. E = 0.636 with δ chosen as 0.001. (b) Plot of Δ′-r. E = 0.638 with δ chosen as 0.001.

From Fig. 2(a), we can see the real solution does not exist anymore. This implies that the event horizon is destroyed and the naked singularity is produced after absorbing a test particle. On the other hand, if we chose E is 0.638, which is slightly larger than the E_max, with δ chosen to be 0.001, we get the plot of Δ′-r in Fig. 2(b), which shows there are two different solution of Δ′. This means after capturing a test particle, the extremal black hole will have inner horizon and outer horizon. Thus it turns into a common black hole. This implies when the energy of test particle located in [0.635 641, 0.637 13], the black hole will be destroyed.

Next, we will show that a particle from infinity whose energy between E_max and E_min could really fall into the black hole. Since the metric is axisymmetric, the test particle can fall along the orbit which lying entirely in the plane θ = π/2. For such an orbit, one can solve Eq. (20) for ,^[9] and obtain

Fig. 3

	Figure Option ViewDownloadNew Window
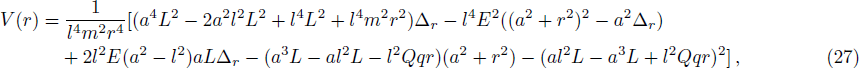
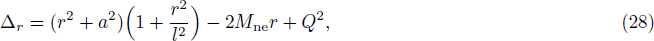
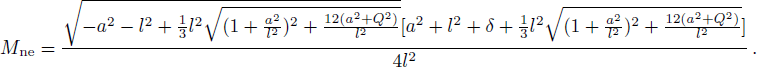
	Fig. 3 The effective potential V(r) of a test particle outside event horizon with 4 ˂ r ˂ 10. Test particle’s energy Emin ˂ E ˂ Emax.

Figure 3 shows curve is descending and the particle is easy to fall into a Kerr-Newman-AdS black hole from infinity. The choice m = E indicates that the particle stays at rest relative to a stationary observer at infinity, so it is realizable in practice.

In this paper, we have found that a test particle may destroy the horizon of a near-extremal Kerr-Newman-AdS black hole, resulting in an apparent violation of the cosmic censorship without taking into account the radiative and self-force effects. Moreover, the allowed range for the particle’s energy E to destroy the black hole is narrow, which indicates that the energy of the particle must be finely tuned. Generally, it regards that taking the radiative and self-force effects^[28–30] into account could compensate for the WCC violations.

It is worth to point out that in Refs. [9–10, 27], the higher order term in evaluating the allowed upper limit of particle’s energy E_max is neglected. While in our paper, we sacrifice the analyticity of E_max and use the numerical method, so we can plot the allowed range for test particle’s energy to destroy the Kerr-Newman-AdS black hole without approximation. Figure 1(b) we obtained is similar to Fig. 4.1 in Ref. [27], both of Fig. 1(b) and Fig. 4.1 show ΔE is very narrow and gets narrower as δ increases in the near extremal case.

Nevertheless, the analysis performed in this paper neglects the radiative and self-force effects. The fact that ΔE is very small leaves the possibility of radiative and self-force effects considerations to cure the problem of WCC violation in Kerr-Newman-AdS spacetime. We will address these projects in our future work.