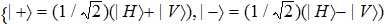Quantum systems can have correlations different from those of classical systems. Considering two separated observers, Alice and Bob, sharing a quantum state, each chooses one from a set of possible measurements and obtains some outcomes. In the quantum states with the property of being entangled, Alice and Bob can observe correlations, which cannot be explained by classical models defined in terms of local hidden variables. These non-local correlations can be detected by observing violations of the CHSH inequalities.^[1–5] A key feature of nonlocal correlations is that it does not allow the two observers to send information to each other faster than light, i.e., correlations from the measurements on quantum states are non-signaling.

Assuming local realism, the correlations predicted by quantum mechanics cannot violate the CHSH inequality beyond Tsirelson’s bound 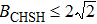.^[6] In 1994, Popescu and Rohrlich^[7] (PR) presented a nonphysical correlation which violates CHSH inequality by its algebraic maximum 4. This result illustrates that, the set of quantum correlations, which are stronger than those of local correlations, is still a subset of a bigger set of more general non-signaling correlations, which can reach the algebraic maximal violation of Bell-type inequalities.^[8] Although these post-quantum correlations cannot be implemented by classical or quantum systems,^[9–12] they can be simulated by making use of the loopholes in a Bell test or enlarging Hilbert space and making use of some kinds of post-selection. The fair-sampling loophole (or detection loophole) has been used to simulate the violations of Bell inequality beyond Tsirelson’s bound in different ways.^[13–20] We found that the fair-sampling loophole is generally opened by the selection of states to be measured, meanwhile the fair-sampling loophole still can be opened by the selection of the results after measurement. Although enlarging Hilbert space and making use of some kinds of post-selection can open the fair-sampling loophole via the selection of the results after measurement,^[21–22] enlarging the Hilbert space will inevitably increase the realization complexity of the simulation scheme. For instance, Cabello proposed a scheme for simulating bipartite correlations whose violations of CHSH inequality can surpass Tsirelson’s bound via appropriately post-selecting two qubits from a three-qubit GHZ state system,^[21] and these post-quantum correlations were observed in optical system experimentally.^[22] But this kind of simulation process must resort to enlarging the Hilbert space and post-selecting the measurement results, which obviously limits its persuasiveness. If this kind of simulation can be done directly on the two subsystems in a bipartite entangled state, the simulated bipartite post-quantum correlations are just among the two subsystems, and thus it can be understood in a clearer way. In addition, if the Hilbert space is not enlarged, the simulation scheme can be simplified. So in this paper, we want to study how to simulate bipartite post-quantum correlations by using the fair-sampling loophole opened by the selection of the results after measurement without enlarging the Hilbert space. That is to say, the simulation of post-quantum correlations can be done directly on two subsystems of a bipartite entangled state, and no auxiliary Hilbert space is involved, which can reduce the realization complexity of the scheme. Furthermore, the fair-sampling loophole is opened by post-selecting the results after measurement, which is more feasible than the selection of the states to be measured before measurement. This new simulation scheme of post-quantum correlations is made possible by introducing the “two-state vector formalism” of quantum mechanics.^[23–25] The “two-state vector formalism” is a complete description of a quantum system at a given time based on the results of experiments performed both before and after this time,^[23–24] and it equips us to simulate post-quantum correlations with bipartite entangled states. Here under the “two-state vector formalism”, we present a physical realization of postcorrelations by exploiting the fair-sampling loophole of Bell test opened by the selection of the results after measurement in bipartite optical system. The protocol is realized by quantum non-demolition measurements of photon polarization via cross-Kerr nonlinearity, which has been used extensively in quantum information processing, such as exploration of photon-number entangled states,^[26] recyclable amplification for single-photon entanglement from photon loss and decoherence,^[27] distributed secure quantum machine learning and generation of the entangled state.^[28–31] The key steps of our scheme are preparation and verification of EPR states of photons, which have been demonstrated in teleportation experiments.^[32] By pre- and post-selecting maximally entangled states, the maximally allowed violation of the CHSH inequality 4 can be reached. The result does not conflict with quantum mechanics because of the pre- and post-selections, which equips us not only to violate CHSH inequality but also to surpass the Tsirelson’s bound. Our simulation scheme shows that the fair-sampling loophole is naturally opened in the “two-state vector formalism” of quantum mechanics, which can be used to simulate the bipartite post-quantum correlations without introducing auxiliary Hilbert space. The results presented here open a new way to mimic post-quantum correlations.

Quantum measurement^[33–34] plays an essential role in extracting information from a physical system of interest. To observe the post-quantum correlations in quantum systems, pre- and post-selected ensembles must be prepared.^[25] That is to say, the generalized description of a quantum system in the time interval between two measurements must be introduced,^[23–24] where the generalized state completely describes a quantum system when information about the system is available both from the past and from the future. For a given pre- and post-selected ensemble, suppose the initial state is |ψ_i⟩ and the final state is |ψ_f⟩, and thus the probability for an outcome |c_n⟩ of an ideal measurement on an observable C at intermediate time is given by ABL formula:^[23–24]

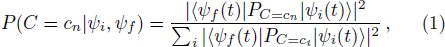
In what follows, we describe in detail how to obtain supercorrelations in pre- and post-selected photon ensembles. Consider a two-photon system whose initial and final states are

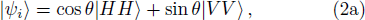
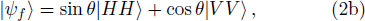
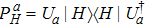
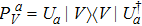
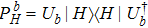
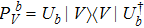
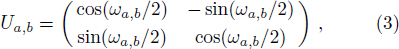
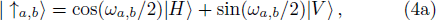
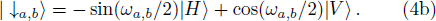
For a given system, the CHSH value is defined as B_CHSH = |C(A, B) − C(A, B′) + C(A′, B) + C(A′, B′)|,^[1] where A and A′ are two-valued (±1) variables for the first system, and B and B′ are similar variables for the second system. The function C(A, B) = P_AB(1, 1) + P_AB(−1, −1) − P_AB(1, −1) − P_AB(−1, 1) represents the expected value of A and B for the two systems, and P_AB(1, 1) denotes the joint probability of obtaining A = 1 and B = 1 when A and B are measured.

According to the ABL formula (1), the correlations of two observables A and B measured by Alice and Bob are given by

Fig. 1

	Figure Option ViewDownloadNew Window
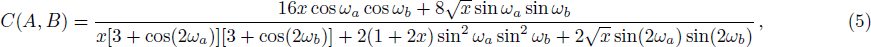
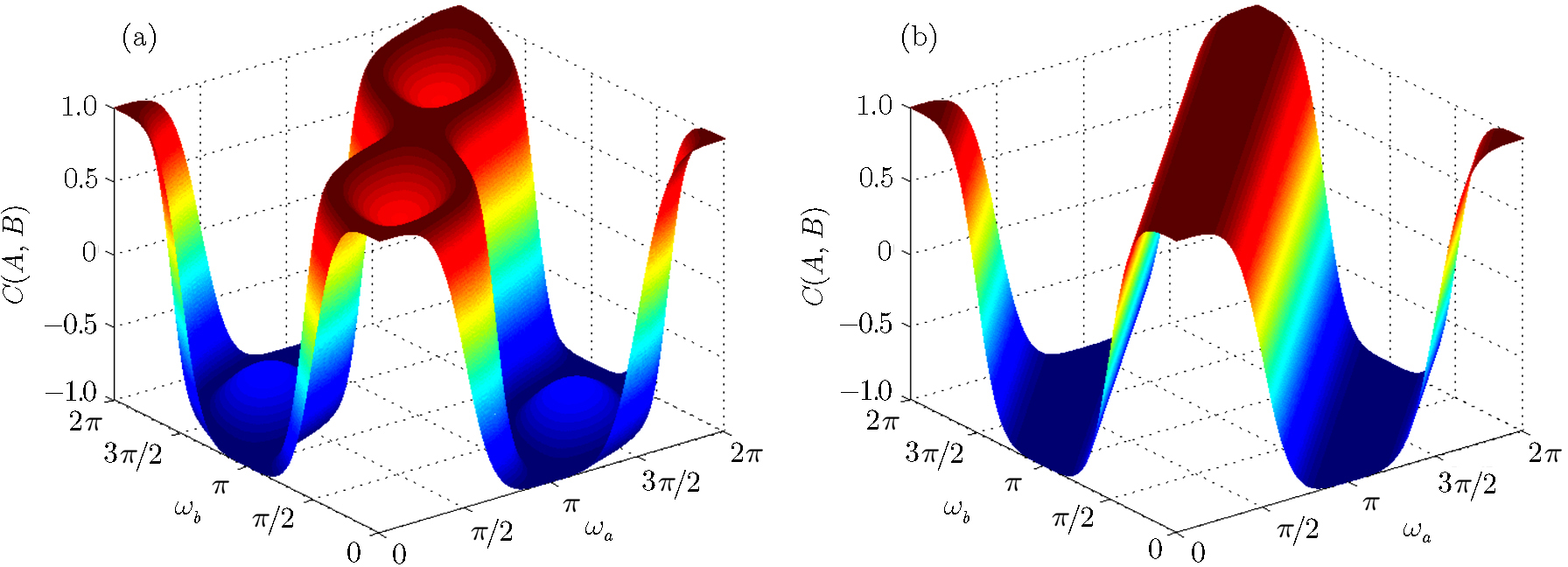	Fig. 1 The correlations C(A, B) are plotted as functions of the parameters of the intermediate measurements ωa, ωb and the parameter x of the initial and final states. (a) x = 0.05, (b) x = 0.25.

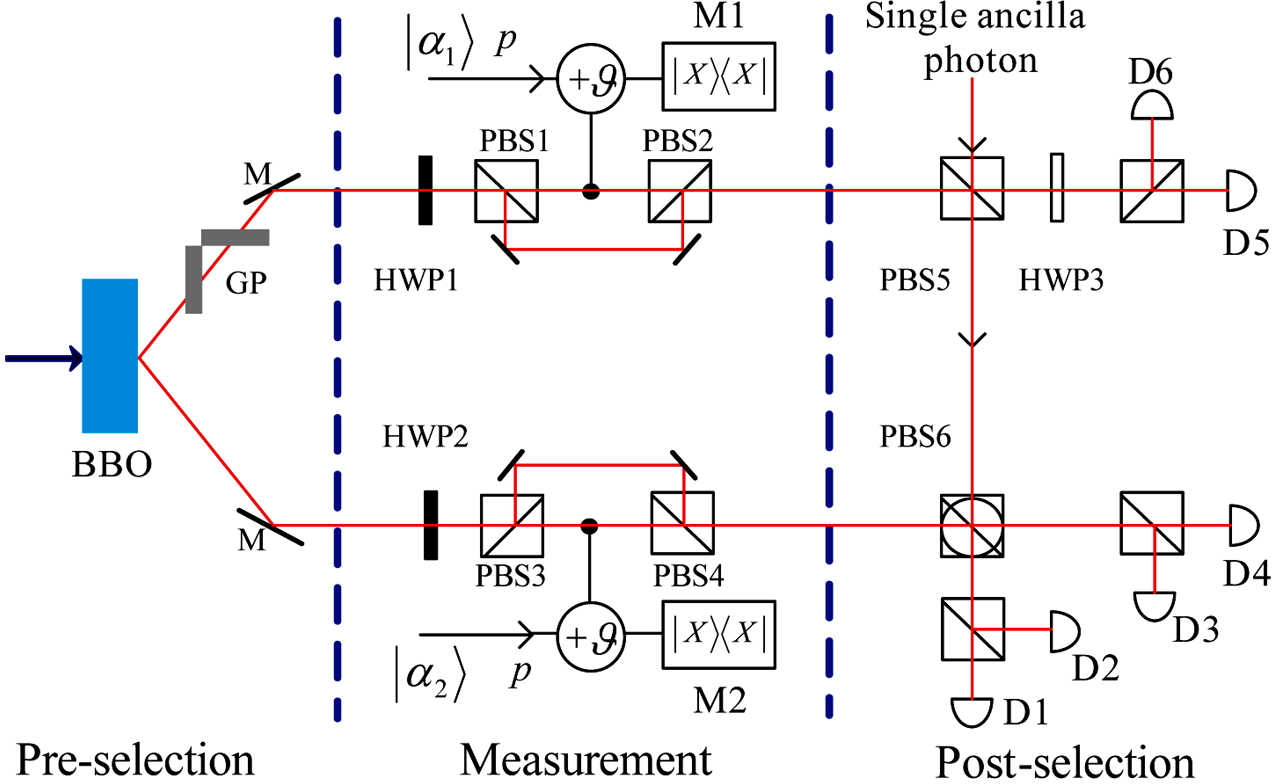
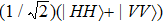
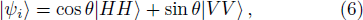
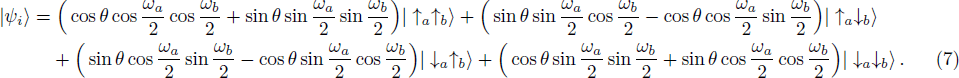
In order to realize two-photon supercorrelations in pre- and post- selected ensembles, three steps are needed, as illustrated in Fig. 2. The first step is pre-selection. Initially, prepare two photons in the Bell state via Spontaneous Parametric Down Conversion (SPDC) process, and then one of the two photons will go through a set of glass plates (GP^[35–36]), which can be tilted to adjust the amount of the polarization-dependent loss. As discussed in Ref. [25], to realize the violation of CHSH inequality as close as possible to 4, the pre- and post-selected states of the ensembles must be some non-maximally entangled states. Thus the two-photon maximally entangled state must be transformed into the following non-maximally entangled state

Fig. 2

Figure Option ViewDownloadNew Window

Fig. 2 Schematic setup for realizing supercorrelations. HWP1 and HWP2 realize the basis transformation | ↑⟩(| ↓ ⟩) ↔ |H⟩(|V ⟩). HWP3 rotates the photon polarization as |H⟩ ↔ sin θ|H⟩ + cos θ|V ⟩, |V ⟩ ↔ −cos θ|H⟩ + sin θ|V ⟩. The + ϑ represents the cross-Kerr nonlinear interaction between the signal photon and the probe coherent beam, where the signal photon will induce a phase shift + ϑ on the coherent beam |α1,2⟩p in the probe mode. |X⟩⟨ X| represents an X quadrature homodyne measurement. PBSi (i = 1, 2, 3, 4, 5) are polarizing beam splitters in {|H⟩, |V ⟩} basis, and PBS6 works in the } basis.

The second step is to realize the local measurements of the photonic states in the basis of Eq. (4) without absorbing the photons, which can be implemented by half-wave plates, cross-Kerr nonlinear interactions between signal photons (entangled photons here) and the probe light beams, and the detection of probe beam. After the entangled photons being distributed to Alice and Bob, they each will perform a quantum non-demolition measurement on the photon polarization via cross-Kerr nonlinearity. Here the half-wave plates (HWP) 1, 2, with their axes set at α = ω_a,b/4 with respect to the horizontal direction, rotate the photon polarization as |H⟩ ↔ | ↑⟩, |V ⟩ ↔ | ↓⟩. After the photons passing through the HWPs 1, 2, respectively, the state of the two photons becomes

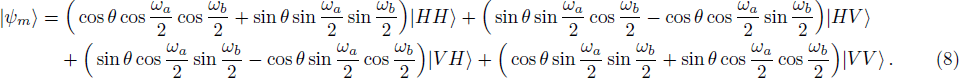
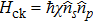
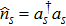
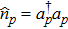
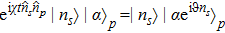
The probe beam is initially prepared in a coherent state, and the interaction between the signal photon and the probe beam will induce a phase shift on the coherent state of the probe beam. Moreover, this phase shift is proportional to the number of the signal photons. The nonlinear interaction between a signal mode and a probe beam can be generally described by the Hamiltonian ,^[37–39] where χ is the coupling strength of the nonlinear interaction, which depends on the cross-Kerr material. and are photon number operators for the two interacting modes (signal mode s and probe mode p). This interaction implies the coherent state |α⟩p in the probe mode accumulates a phase shift n_s ϑ directly proportional to the number of photons n_s in the signal mode, where ϑ = χ t, and t is the interaction time. The evolution of the combined system caused by cross-Kerr nonlinearity can be written as . The polarization beam splitter (PBS) transmits only the |H⟩ polarization component and reflects the |V⟩ polarization component of photons. This is to say, when the signal photon is in |H⟩ state, it will interact with the probe beam via the cross-Kerr nonlinear media, thus induce a phase shift + ϑ on the coherent beam |α⟩_p in the probe mode. On the contrary, when the signal photon is in |V⟩ state, it will be reflected by the PBS and not interact with the probe beam. So there will be no phase shift on the coherent beam |α⟩_p in this case. In this sense, the |H⟩ and |V⟩ states can be discriminated by the detection of the phase shift on the probe coherent beam.

After X quadrature homodyne measurements being performed on the probe beams, the two-photon state will collapse into one of the following four basis states: |HH⟩, |HV⟩, |VH⟩, |VV⟩. Then we can move to the last step—post-selection.

To realize the supercorrelations, the post-selection measurement basis must be chosen as:

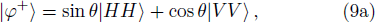
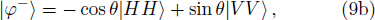
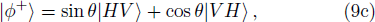
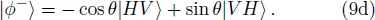
Under the above basis, the collapsed two-photon states can be re-expressed as:

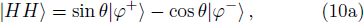
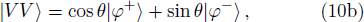
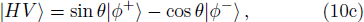
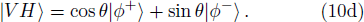
In order to post-select the two-photon states, the four two-photon states |φ⁺⟩, |φ⁻⟩, |ϕ⁺⟩, |ϕ⁻⟩ must be distinguished in this step. To realize this state discrimination process, a PBS, a circular PBS, an HWP, and three photon detectors are needed. The PBS5, circular PBS6 and the HWP3 will transform the joint entangled basis in Eq. (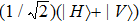9) into the product basis |HH⟩, |HV⟩, |VH⟩, |VV⟩ with the help of an ancilla photon in the superposition state .^[40] The HWP3, with its axis set at β = (π/2 − θ)/2 with respect to the horizontal direction, rotates the photon polarization as |H⟩ ↔ sin θ|H⟩ + cos θ|V ⟩, |V ⟩ ↔ −cos θ|H⟩+sin θ|V ⟩. The output photons will be measured using polarization analyzers (PBSs) followed by single-photon detectors. A click on D1 means that a controlled NOT operation between the two signal photons succeeds with the help of the ancilla photon. So, after the HWP3, the two-photon state will evolve as follows |φ⁺⟩ → |HH⟩, |φ⁻⟩ → |V H⟩, |ϕ⁺⟩ → |HV ⟩, |ϕ⁻⟩ → |V V ⟩. In this way, the post-selected state is ensured.

To understand the relation between the supercorrelations and the measurement outcomes better, we give a brief explanation of how the process realizes the supercorrelations. Assume Alice and Bob share many copies of the pre-selected state |ψ_i⟩ = sin θ|HH⟩ + sin θ|VV⟩. Firstly, they pick up one copy and perform indirect measurements (M1, M2) of the polarization state of each photon under a certain basis (| ↑_a,b⟩, | ↓_a,b⟩), and obtain the outcome (x, y), where x = 1 or −1, y = 1 or −1. Then the photons go through PBS5, PBS6 and HWP3. After interacting with an ancilla photon, the two signal photons and the ancilla photon are detected by the detectors D1,D2,D3,D4,D5 and D6. The coincidence measurement among M1, M2, D1, D4, D5 indicates that the measurement outcome (x, y) of the pre- and post-selected state is (|HH⟩), i.e. (1,1). Similarly, the coincidence measurement among M1,D1,D4,D5 indicates the outcome (1, −1), the coincidence measurement among M2,D1,D4,D5 indicates the outcome (−1, 1), and the coincidence measurement among D1,D4,D5 indicates the outcome (−1, −1). The counting rate of (x, y) is proportional to the conditional probability P_AB(x, y). To measure other components of the conditional probabilities P_A′B(x, y), P_AB′(x, y) and P_A′B′(x, y), one can rotate the HWP1, 2 by ω_a′,b/4, ω_a,b′/4 and ω_a′,b′/4, respectively. Finally, with the obtained condition probabilities and the expected values, the CHSH value 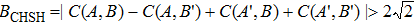, i.e. the supercorrelations are obtained. By selecting different parameter θ of the pre- and post-selected states, different violations of CHSH inequality can be achieved as shown in Eq. (2).

In practical experiment, the entanglement source produced by SPDC is not always perfect, which usually generates an entangled state of the form^[41–42]

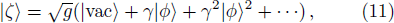
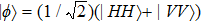
We proceed by considering two-photon ensembles with a maximally entangled initial and final state.

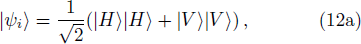
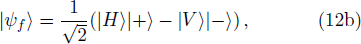
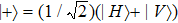
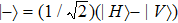
The physical realization of the PR correlation includes three steps. Firstly, the maximally entangled bi-photon state 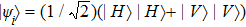is prepared via the SPDC process, and then the two photons will be sent to Alice and Bob, respectively. Secondly, Alice (Bob) performs the measurement on her (his) photon along the z (x) axes, which can be realized via cross-Kerr nonlinearity. By adjusting the angles of the axes of the HWPs 1, 2 with respect to the horizontal direction at 0° or 22.5°, the measurement along the z or x axis direction can be accomplished. The whole process has been described in detail in Sec. 3. After X quadrature homodyne measurements being performed on the probes, the two-photon state will collapse into one of the following four states: |HH⟩, |HV⟩, |VH⟩, |VV⟩.

The set of post-selection measurement basis must be chosen as:

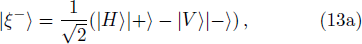
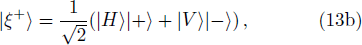
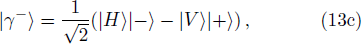
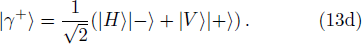
Under the above basis, the two-photon state can be written as:

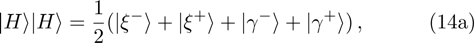
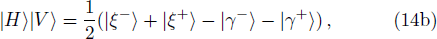
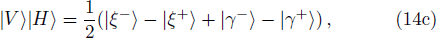
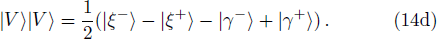
Thirdly, they verify the final state. The final state |ξ⁻⟩ will be post-selected as follows. In order to distinguish states |ξ⁺⟩, |ξ⁻⟩, |γ⁺⟩, |γ⁻⟩ by direct measurements, Alice and Bob need to perform two Hadamard operations and one controlled-not operation 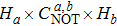on the two photons, which realizes |ξ⁻⟩ → |V H⟩, |ξ⁺⟩ → |HH⟩, |γ⁻⟩ → |V V ⟩, |γ⁺⟩ → |HV ⟩. Thus the correct final state can be distinguished by the direct measurements.

In this paper, we designed an implementation scheme for simulating postquantum correlations by exploiting the fair-sampling loophole in Bell test of bipartite states, which is opened naturally in the “two-state vector formalism” of quantum mechanics without introducing auxiliary Hilbert space, and we can get the probability distributions not only violating CHSH inequality but also surpassing the Tsirelson’s bound. Under the “two-state vector formalism”, the fair-sampling loophole of Bell test is opened by the selection of the results after measurement, which is different from the currently existing simulation schemes for postquantum correlations where the fair-sampling loophole is opened by pre-selecting the states to be measured. Our results verify that the selection of the results after measurement can open fair-sampling loophole too, which can be used to simulate postquantum correlations as well. In addition, our scheme diversifies the simulation tools for postquantum correlations.

In addition, we would like to give an analysis about the feasibility of our simulation scheme. The two challenging building blocks of our scheme are the cross-Kerr nonlinearity in the quantum non-demolition measurement and the Bell state analyzer of the post-selection step. The complete Bell state analyzer needs an optical controlled NOT operation, which has been realized.^[40,45–46] Although the success probability of the complete Bell state analyzer is only 1/8 within the current technology, the four Bell states can be completely discriminated with fidelity reaching 89% when it succeeds. Nonetheless, the low success probability of the Bell state analyzer does not affect the current scheme because we only count the events where the coincidence measurement succeeds. On the other hand, the cross-Kerr nonlinearity is still a controversial topic within current technology. One reason is that the natural cross-Kerr nonlinearity is extremely weak, so it is difficult to discriminate the two overlapping coherent states in homodyne detection. Fortunately, some theoretical works have proved that with the help of weak measurement, it is possible to amplify the phase shift induced by single photon to an observable value.^[47–48] Recently, the single-photon-level nonlinear phase shift in an optical fibre has been demonstrated experimentally, which uses the photonic crystal fibre as a Kerr medium as it has a high capacity for confining light in its silica core.^[49] Of course, there will be errors in the homodyne measurement on coherent probe beams due to the fact that the coherent state |α⟩ and the phase-shifted coherent state of the probe mode are not completely orthogonal, and this error probability is given by .^[38] In fact, for αδ ∼ π this discrimination error P_error ∼ 10⁻³, which is much smaller than other errors. In addition, the model used here is the cross-phase modulation version of the single-mode quantum treatment of self-phase modulation, so the noise caused by the causal, noninstantaneous nature of the response functions on the utility of such cross-Kerr nonlinearities does not affect the feasibility of our scheme.^[50]