† Corresponding author. E-mail:
The searching exact solutions in the solitary wave form of non-linear partial differential equations (PDEs) play a significant role to understand the internal mechanism of complex physical phenomena. In this paper, we employ the proposed modified extended mapping method for constructing the exact solitary wave and soliton solutions of coupled Klein-Gordon equations and the (2+1)-dimensional cubic Klein-Gordon (K-G) equation. The Klein-Gordon equations are relativistic version of Schrödinger equations, which describe the relation of relativistic energy-momentum in the form of quantized version. We productively achieve exact solutions involving parameters such as dark and bright solitary waves, Kink solitary wave, anti-Kink solitary wave, periodic solitary waves, and hyperbolic functions in which several solutions are novel. We plot the three-dimensional surface of some obtained solutions in this study. It is recognized that the modified mapping technique presents a more prestigious mathematical tool for acquiring analytical solutions of PDEs arise in mathematical physics.
Nonlinear partial differential equations exist in all fields of engineering and science, such as optical fibers, fluid mechanics, plasma physics, chemical kinematics, biology, chemical physics etc. and also utilized to describe the complex aspects in these areas. Thus, the study to search for exact solutions of nonlinear PDEs is extremely crucial. Therefore, to search efficient techniques to construct analytic of non-linear PDEs have pinched a plenty of curiosity via a diverse group of scientists and researchers. Several symbolic techniques have been developed by different researchers and employed to get the exact solutions of nonlinear PDEs in different form, for example; Bäcklund transformations,[1] variational method,[2] Darboux transformation,[3] modified direct algebraic method,[4–5] auxiliary and simple equation methods,[6–7] Hirotas bilinear method,[8] trial equation technique,[9] inverse scattering scheme,[10] the extended tanh method, the generalized Kudryashov method,[11] (G′/G)-expansion method,[12] mapping method,[13] expansion method,[14] and many more.[15–19] In general, there are numerous researchers organized in the area of non-linear science.[20–21] Solitons solutions got more attention of researchers about the study interactions, structures, and more properties.[22–28]
The mean of the current study is to utilize the powerful proposed mapping method for the Klein-Gordon equations. As a result, novel exact solutions in more generalized and different form are obtained. Modulation instability analysis is employed to argue discuss the stability of solitary are solutions in both the normal dispersion and the anomalous regime.
The coupled Klein-Gordon equations:[29]
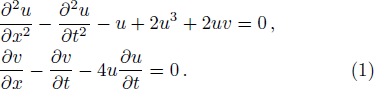
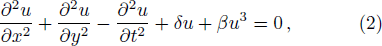
The rest of paper is ordered as follows. In Sec.
In this section, we will present the algorithm of modified extended mapping method for nonlinear partial differential equations (PDEs). Let us assume a non-linear PDE in general form having two independent variable x and t as
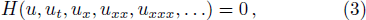
Performing the traveling wave transformation u(x,t) = U(ζ), v(x,t) = V(ζ) and ζ = k (x − ωt) on Eq. (
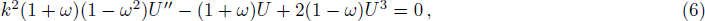

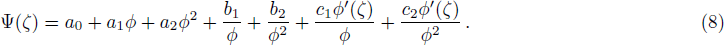
The following traveling wave solutions of Eq. (
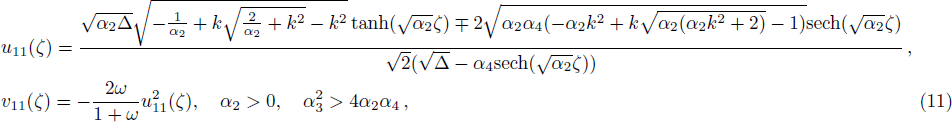
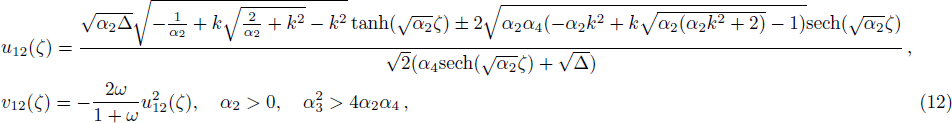
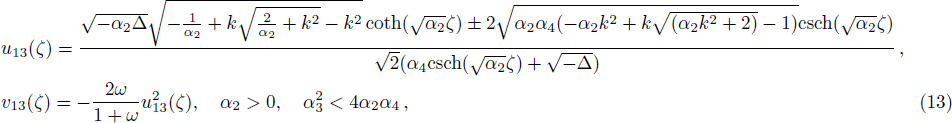
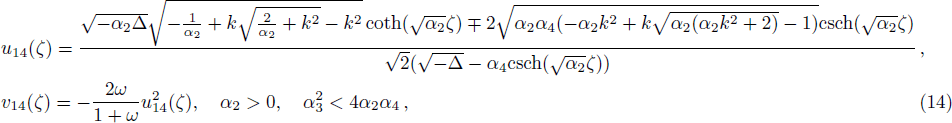
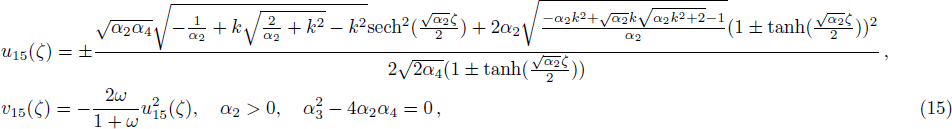
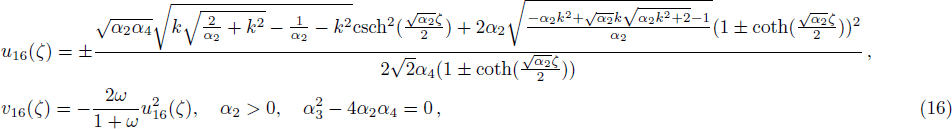
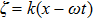
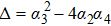
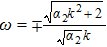
One can construct more solitary wave solutions of Eq. (
We obtained solitary wave solutions of Eq. (
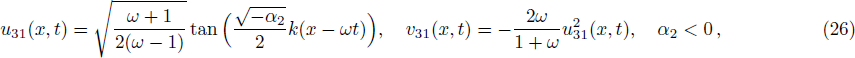
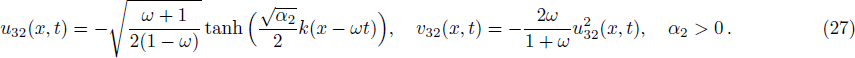
We obtain solitary wave solutions of Eq. (
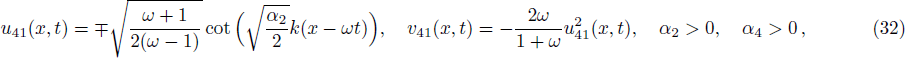
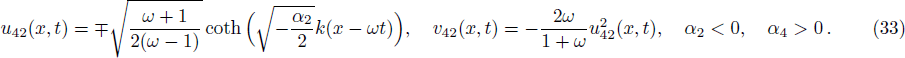
Performing the transformation u(x,y,t) = U(ζ) and ζ = k1x + k2y − ωt on Eq. (

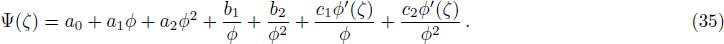
We construct solitary wave solutions of Eq. (
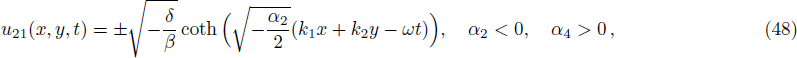
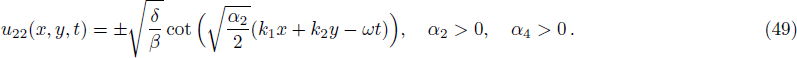
The following traveling wave solutions of Eq. (
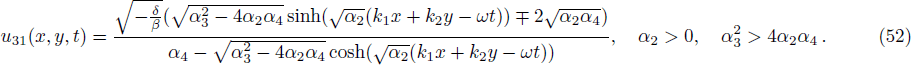
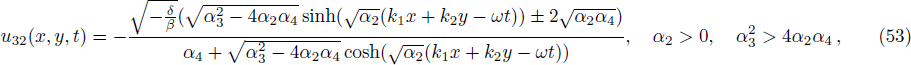
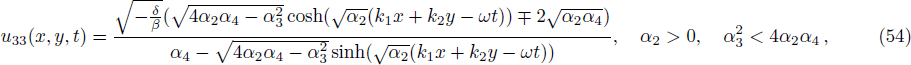
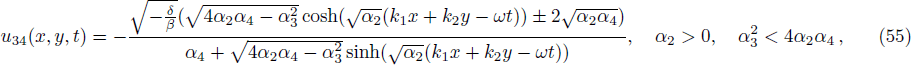
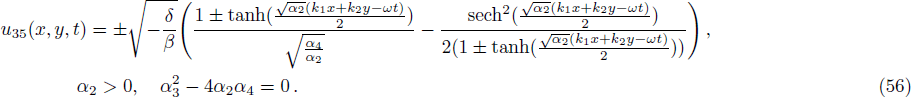
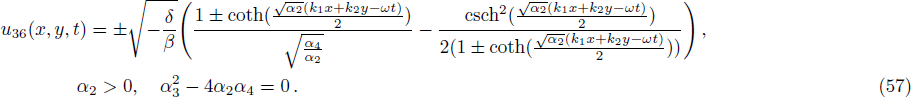
We construct solitary wave solutions of Eq. (
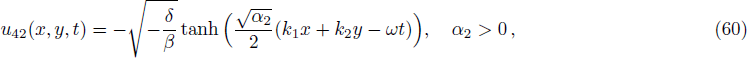
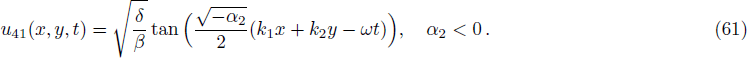
Several non-linear evolution equations of higher order illustrating an instability that directs to examine the modulation of the steady state as a results of interaction among the dispersive and non-linear effects. The modulation instability of coupled K-G equations and cubic K-G equation are studied by utilizing linear stability analysis (LSA).[31–33]
The study state solution of coupled Klein-Gordon equation has the form
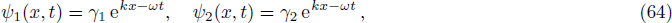
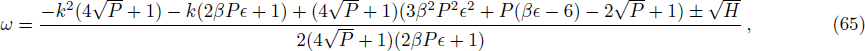
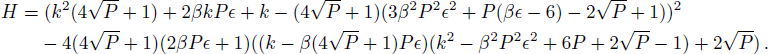
The dispersion relation Eq. (
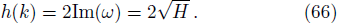
The study state solution of (2+1)-dimensional cubic Klein Gordon equation has the form
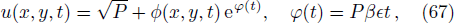
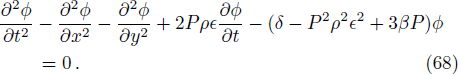
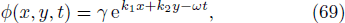
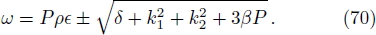
The dispersion relation equation (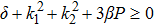
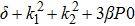
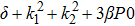
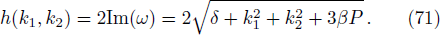
In this section, we discuss the obtained exact solutions and analyse it with the existing in the literature.
Firstly, for the coupled Klein-Gordon equations; the authors in Ref. [29] used the modified simple equation method (MSEM) and achieved some exact solutions in solitary wave form with functions of trigonometric and hyperbolic structure. The obtained solutions (
Secondly, for the cubic Klein-Gordon equation; the authors in Ref. [30] also employed the MSEM to this equation and achieved some exact solutions. The obtained solutions (
Analyzing our solutions with the above stated solutions for both models, we determined that our exact solutions are newly constructed solutions with some important physical meaning, for instance; the tangent hyperbolic occurs in the cal-culation of magnetic moment and immediateness of special relativity, the secant hyperbolic occurs in the laminar jet profile and the sine hyperbolic occurs in the gravitational potential of a cylinder and the calculation of Roche limit.[34]
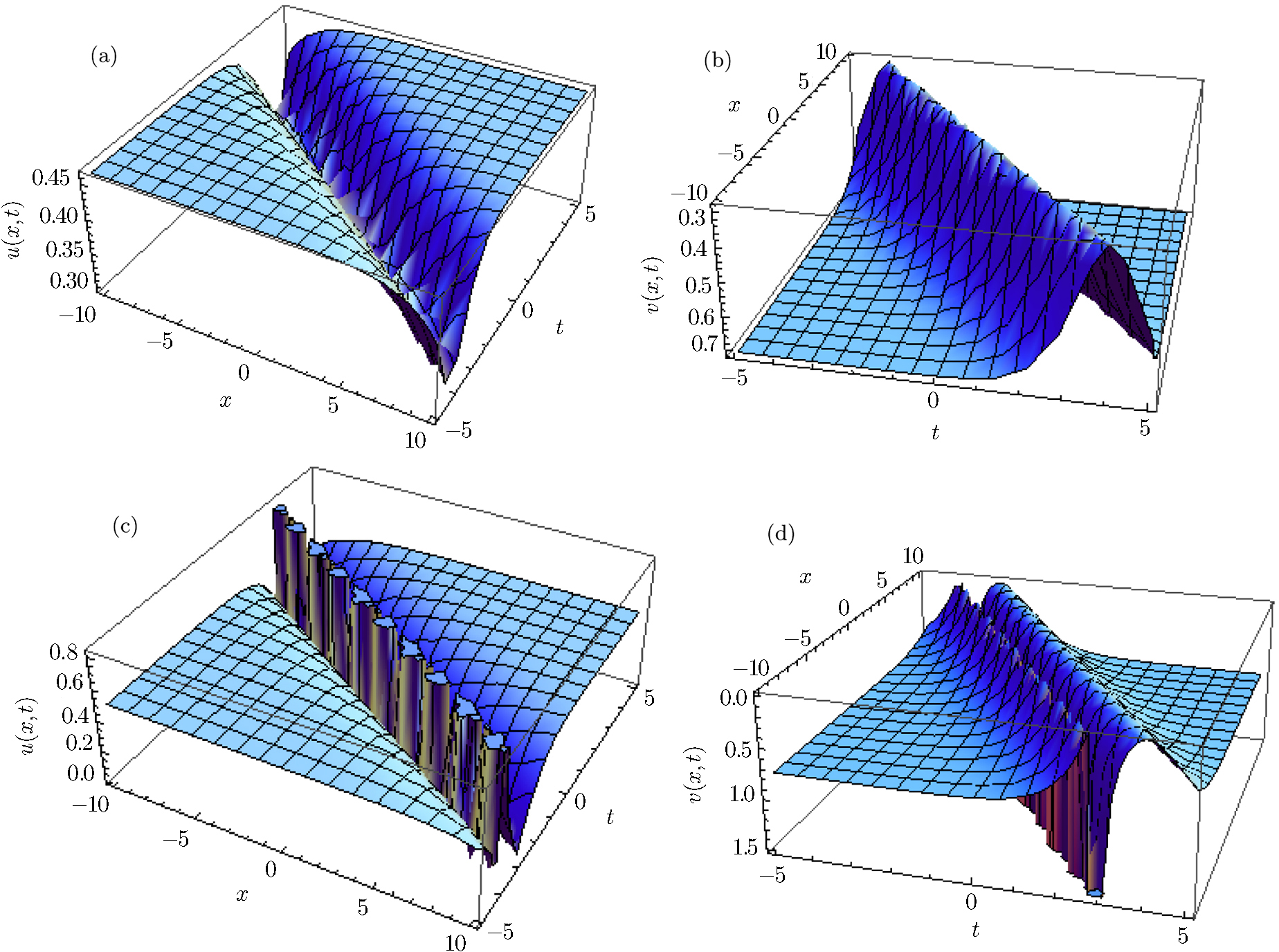
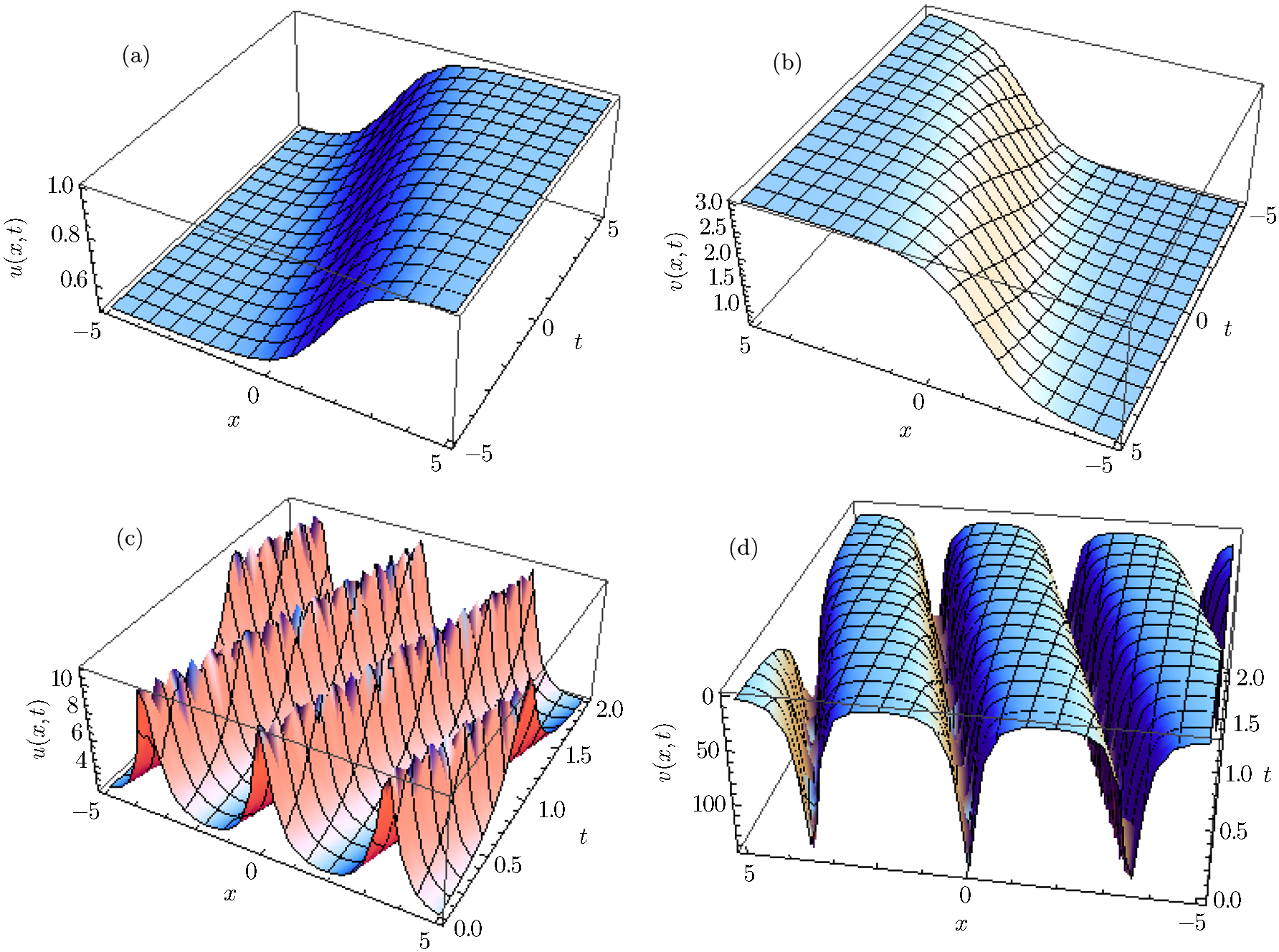
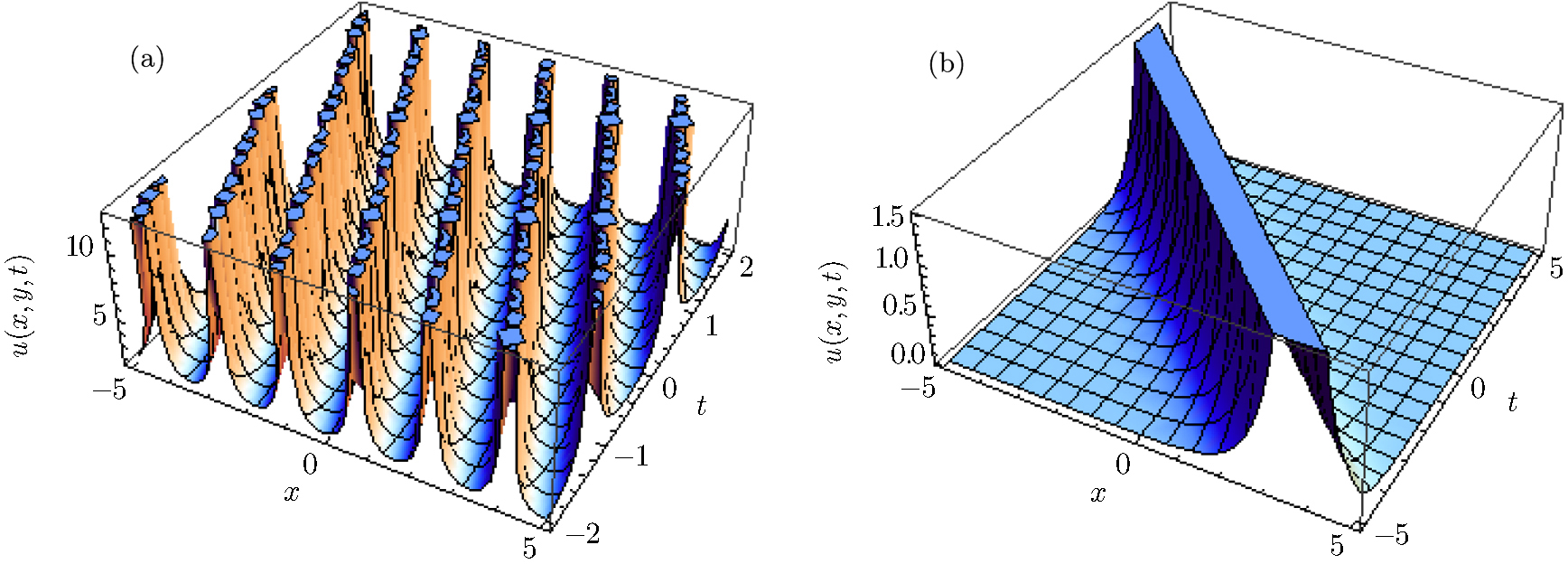
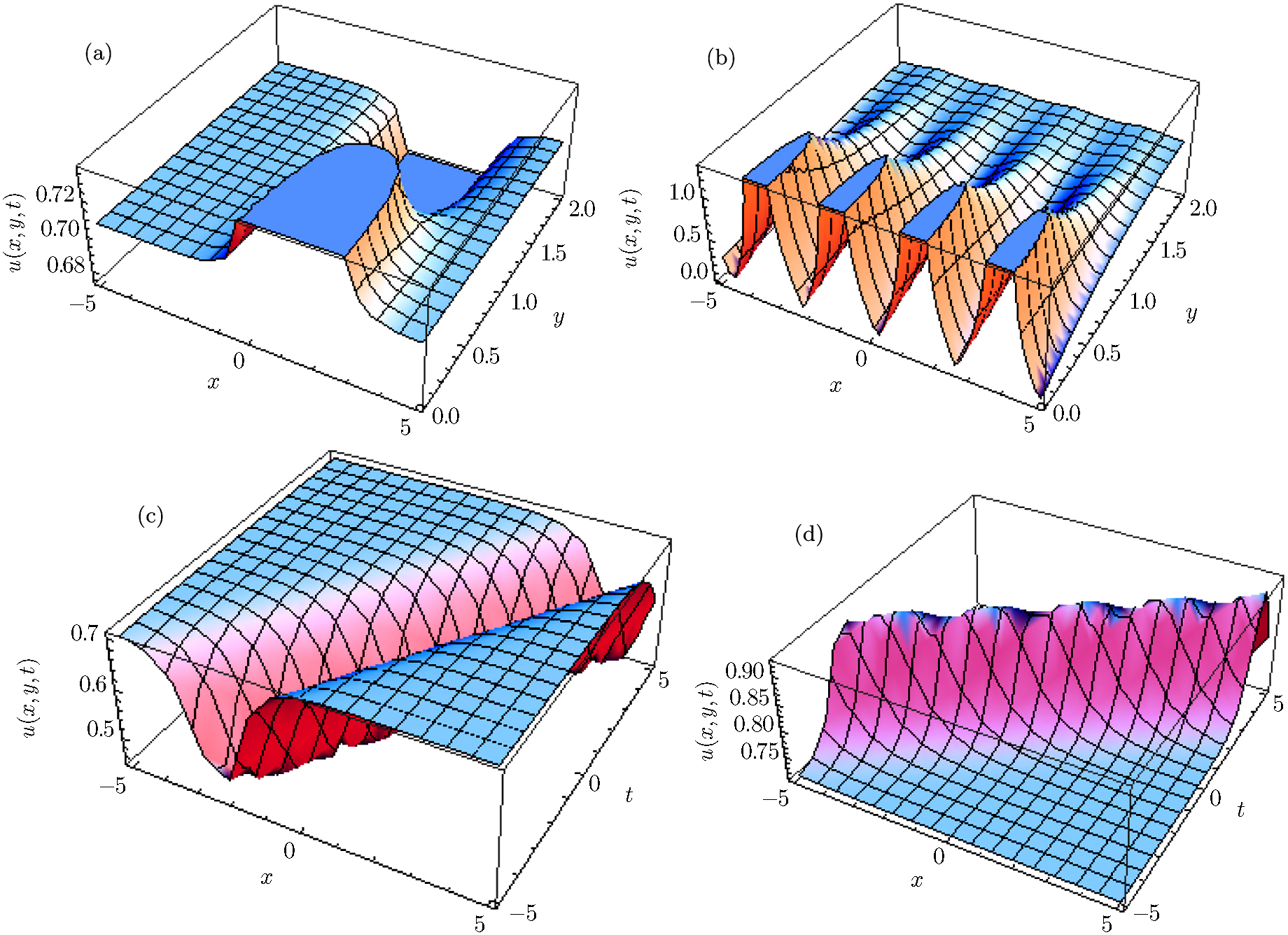
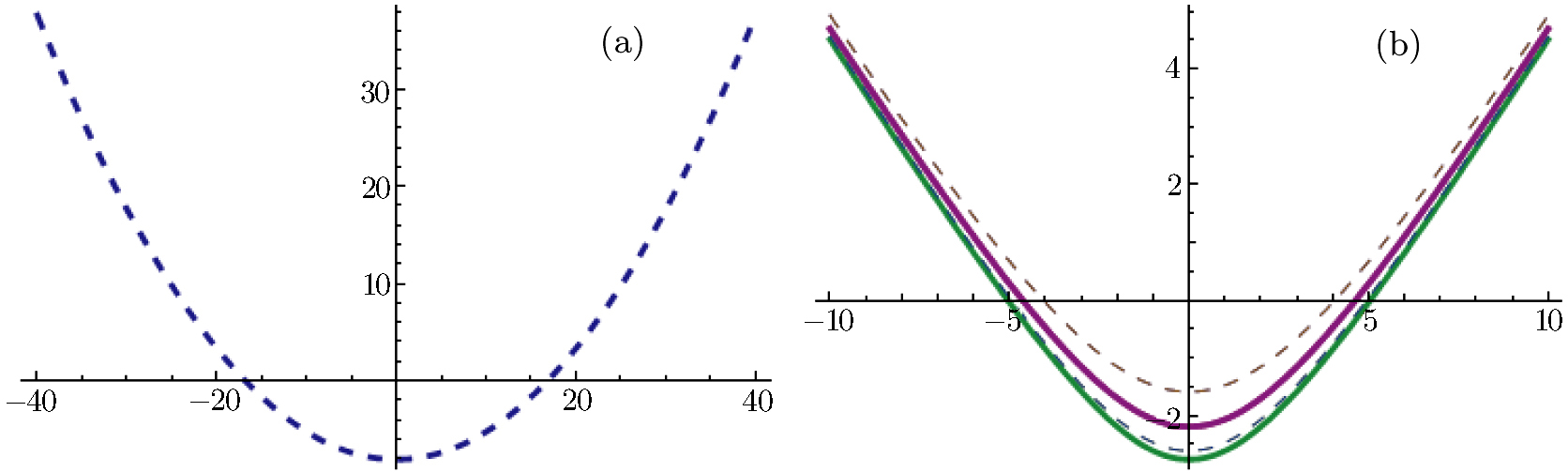
In Fig.
In Fig.
In this article, we successfully implemented the powerful proposed modified extended mapping method to achieve the solitary wave solutions of the coupled K-G and cubic K-G equations. The obtained solutions are more general and in different forms such as the solitary waves in the form of bright and dark, periodic, hyperbolic etc. We compared our solutions with the existing solutions to these two models and claimed that many solutions are novel. The equations admit the enormous diversity of possible solutions for only values of a small subset of parameters, which helps to understand the physical phenomena’s of this equation. The moments of some solutions graphically and the formation conditions for dark and bright solitons were obtained. An analytic expression for the modulation instability has been established by utilizing modulation instability which confirms that all exact solutions are stable. The efficiency and simplicity of the proposed modified extended mapping method show that it can be used to various types of different nonlinear models that arise in the various areas of nonlinear science.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] |