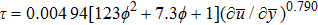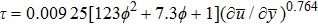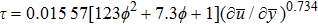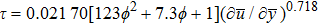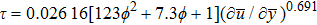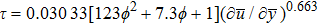Cite this Article
Shehzad N., Zeeshan A., Ellahi R.. Electroosmotic Flow of MHD Power Law Al2O3-PVC Nanouid in a Horizontal Channel: Couette-Poiseuille Flow Model. Communications in Theoretical Physics, 2018, 69(6): 655  
Permissions
Electroosmotic Flow of MHD Power Law Al2O3-PVC Nanouid in a Horizontal Channel: Couette-Poiseuille Flow Model
Shehzad N. *, Zeeshan A., Ellahi R.
Department of Mathematics and Statistics, FBAS, IIUI, Islamabad 44000, Pakistan

 

† Corresponding author. E-mail: nasir.isbrwp@gmail.com

Abstract
Abstract

The current manuscript is reported about the electro-osmotic Couette-Poiseuille flow of power law Al2O3-PVC nanofluid through a channel, in which upper wall is moving with constant velocity. The influences of magnetic field, mixed convection, joule heating, and viscous dissipation are also incorporated. The flow is generated because of constant pressure gradient in axial direction. The resulting flow problem is coupled nonlinear ordinary differential equations, which are at first modeled and then transform into dimensionless form through appropriate transformation. Analytical solution of the governing is carried out. The impact of modified Brinkman number, modified Magnetic field, electro-osmotic parameters on velocity and temperature are examined graphically. From the results, it is concluded that the Skin friction at moving isolated wall decreases with the increase of electro-osmotic parameter and reverse behavior for Nusselt number at heated stationary wall occur.

Keyword:Couette-Poiseuille flow;power law nanofluid;electro-osmotic flow;MHD;PVC;Alumina
Nomenclature

n

Power-law index

Cp

Specific heat at constant pressure [J·kg−1·K−1]

 T

Dimensional fluid temperatuer [K]

 k

Thermal conductivity [W·m−1·K−1]

 F

Net body force per unit votume

 −a, a

Lower, upper walls of channel [m]

 g

Gravitational acceleration [m·s−2]

 V

Dimensional fluid velocity field

 p

Dimensionless pressure

 P

Constant pressure gradient

 B0

Uniform transverse magnemic field [T]

 E

External electric field

 U*

Dimensional upper wall velocity [m·s−1]

 U

Dimensionless upper wall velocity

Dimensional component of velocity [m·s−1]

 u

Dimensionless x component of velocity

 ħu

Embedding parameter for velocity

 ħθ

Embedding parameter for temperature

 K

Consistency index [Pa·s]

 e

Electron charge [C]

 J

Current density [C·m−3]

 kB

Boltzmann constant [mol−1·K−1]

Dimensional pressure [N·m−2]

 Re

Modified Reynolds number

 b

Induced magnetic fields

 Ex

Axial electric field

 2a

Total width of channel [m]

 Gr

Monified Grashof number

 Br

Modified Brinkman number

 M

Modified magnetic field

 n0

Ion density of bulk liquid

 zv

Valence of ions

 Cf

Skin friciton coefficient

Absolute temperature

 Nu

Nusselt number

Greek symbols

{}

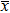
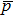
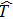
Dimensional electric charge density [C·m−3]

μ

Viscosity parameter [N·s·m−2]

 β

Volumetric volume expansion coefficient [k−1]

 ρe

Dimensional electric charge density

 Γ

Electric potential

 ψ

EDL potential

 ξ1

Zeta potential at lower wall [V]

 θ

Dimensionless temperature

 ϕ

Nanoparticle volume fraction

 Φ

Viscous dissipation

 ρ

Density [kg·m−3]

 ε

Dielectric constant

 σ

Electrical conductivity [S·m−1]

 Ψ

Applied electric potential

 ξ1

Zeta potential at upper wall [V]

 τ

Shear stress [Pa]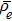

Subscripts

f

Fluid

nf

Nanofluid

 p

Praticle

 w

Wall

1 Introduction

Conventional fluids like water, kerosene, ethylene glycol and acetone etc. plays a pivotal role in many scientific, industrial and engineering applications. Their applications are in the field of chemical production, microelectronics, transportation, and air-conditioning. However, these fluids have limited thermal conductivity due to their low heat transfer characteristics. Various procedures have been adopted to enhance their heat transfer ability. A way to overcome this barrier, the enhancement for heat transfer in conventional fluids via inclusion of nanoparticles in common fluids is one of key achievement of recent era. Nanofluid are heat transfer fluids, which are combinations of particles (e.g., Cu, Ag, TiO2, Al2O3) having size (1 nm–100 nm) suspended in carrier fluid (e.g., propylene glycol, Kerosene oil, water and ethylene glycol), etc. Choi et al.[1] has made pioneering contribution to nanofluids. Later on, Pak and Cho[2] investigated that by 2.78% inclusion of Al2O3 nanoparticles in water, the heat transfer rate will be enhanced 75%. Further Xuan et al.[3] experimentally observed thermal conductivity enhancement in Cu-water nanofluid. They examined that, when 5% volume fraction of nano-size copper particles are suspended in water then thermal conductivity of nanofluid enhanced and stability remains for more than hours without any interruption. Some recent contributions are made on the said topic[4–10] over diverse geometries.

In recent years, electro-osmotic flow of power law nanofluid has gained an immense response of researchers, scientist and industrialists due to its enormous engineering applications. For the prediction of fluid flow with non-Newtonian fluids such as pseudo-plastic and dilatant fluids, the power-law model is frequently used.[11] However, the power-law model does not predict the velocity distribution correctly in the region of lower shear rates. Overcome this deficiency modified power law model[12] used to get the more accurate velocity distribution in the region of lower shear rates also for zero shear rate. Electro-kinetic effects are generated, when the ionized fluid moving with respect to a stationary charged surface under an externally applied electric field is process is called Electro-osmosis. The term electro-osmotic was first time reported in an experimental investigation using the application of an electric field porous clay diaphragm by Reuss.[13] Charge developed on the surface of nano-size particles, which are suspended in base fluid, opposite charge ions to that of the particle surface are attracted, because of the developing charged diffuse layer around the particles called electrical double layer.[14] Zeeshan et al.[15] assumed the electrically conducting fluid with uniform magnetic field in non-uniform two-dimensional channel. They observed that the magnitude of pressure rise is maximum in the middle of the channel whereas for higher values of fluid parameter it increases. Further, it is also found that the velocity profile shows converse behavior along the walls of the channel against multiple values of fluid parameter. However both Newtonian and non-Newtonian electro-osmotic peristaltic transport models[16–19] in presence of electroosmosis have been reported with and without nanofluids.

Heat transfer from the material moving continuously in a channel plays a vital role and has many applications in material processing like as continuous casting, metal forming, extrusion, wire and glass fiber drawing and hot rolling etc.[20–21] In such processes, continuously transport heat with the adjacent fluid and the fluid involved may be Newtonian or non-Newtonian and the flow situations encountered can be either laminar or turbulent. An extensive research works about steady laminar and heat transport to a Poiseuille flow in channel with the static walls has been reported by Shah and London[22] for Newtonian fluids and by Irvine and Karni[11] for non-Newtonian fluids. Couette-Poiseuille laminar, steady state heat transfer flow in parallel plates along with axial movement of one plate and pressure gradient has been examined by Hudson and Bankoff,[23] Sestak and Rieger,[24] Bruin,[25] Davis,[26] and El-Ariny and Aziz[27] for Newtonian fluids. A numerical investigation of fully developed non-Newtonian Couette-Poiseuille flow has been done by Davaa et al.,[28] Hayat et al.[29] and Hashemabadi et al.[30] They established that rate of heat transfer at heated wall is increased by increasing the Brinkman number when the flow direction is same as the movement of upper plate, but the reverse behavior can be seen when the flow direction and upper late are opposite. Marin[31] established a concept for micropolar porous media dependent on heat-flux including void age time derivative among the independent constitutive variables. Author indicated that this heat-flux theory becomes a predictive theory of light scattering, sound dispersion, shock wave structure and so on. It now appears concomitant to the kinetic theory of gases and closely related to the mathematical theory of hyperbolic systems. Forced convection MHD fluid flow around two solid circular cylinders in side by side arrangement and wrapped with porous ring has been investigated by Rashidi.[32] Author concluded that the effect of magnetic field is negligible in the gap between two cylinders because the magnetic field for two cylinders counteracts each other in these regions. Tripathi[33] discussed the influence of viscoelastic behavior, fractional nature of fluid model and transverse magnetic field on peristaltic flow pattern. He established the result that the magnitude of frictional force reduces in very small interval of volumetric flow rate then it increases with increasing magnetic field parameter.

Literature survey revealed that there is no such investigation has been reported on MHD power law nanofluid passed through the two parallel walls one of them is moving. Therefore, our current innovative study represents interesting phenomenon of Couette-Poiseuille flow of power law nanofluid under the influence of MHD. The influences of Ohmic dissipation, viscous dissipation, and electro-osmotic are also accounted. The resulting systems of coupled nonlinear ODEs are tackled through analytical method.[34–36] The following sections consist of problem formulation, solution procedure, convergence analysis, results and discussion, conclusion and references. Also the fallouts of velocity, temperature together with skin friction and Nusselt number are briefly nattered for emerging parameters modied Brinkman number and modied magnetic field at 20-th order iterations.

2 Problem Analysis
2.1 Geometry Description

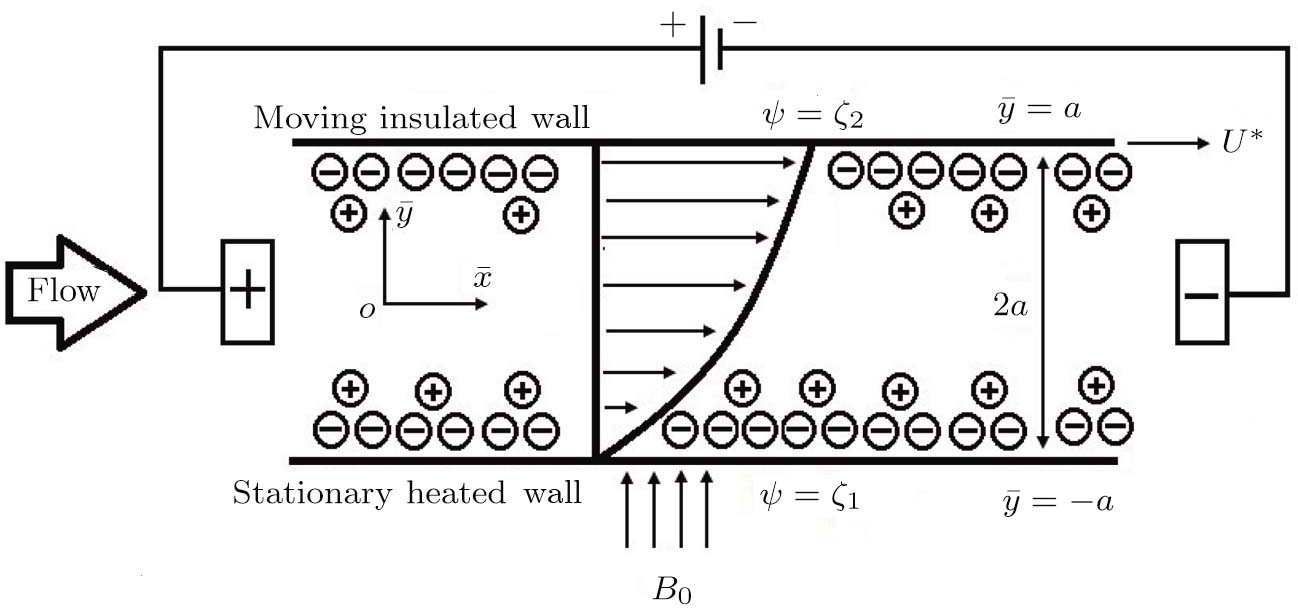
Consider a steady, laminar, viscous, incompressible, hydromagnetic fully developed boundary layer flow of an electrically conductive power-law non-Newtonian nanofluid passed through a channel containing two parallel straight walls at 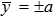as shown in Fig. 1. Consider, upper channel wall is adiabatic and moving with constant velocity U*, whereas constant heat flux qw is taken at lower wall (stationary) of channel.

Fig. 1 Schematic diagram of the flow model.
2.2 Power Law Fluids

In non-Newtonian fluids modeling, the viscous stress is directly but not linearly proportional to the shear rate 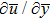, whose direction is perpendicular to the fluid. The viscosity μf of non-Newtonian fluid is described as:

Fluid is pseudo-plastic or shear-thinning for (0<n<1), Newtonian for (n=1) and dilatant or shear-thickening for (n>1). The power law non-Newtonian shear-thinning fluid (Ostwald-de Waele model) is considered to calculate the shear stresses of the nanofluid. In current study for the nanofluid, polymer solution of different concentration of polyvinyl alcohol in water is used as conventional fluid with nanoparticles of Alumina (Al2O3). The thermophysical parameters of base fluid (PVC) and nanoparticles (Al2O3) are given in Table 1.

Table 1

Thermophysical properties of Polyvinyl chloride (PVC)[37] and Al2O3 nanoparticles.[2]

.

The shear stress (τ) of a power-law model is defined as:

2.3 Mathematical Formulation

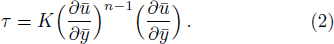
As nature and behavior of nanofluid model define above, the fluid motion is generated because of axial movement of the upper plate, constant pressure gradient and electric body force produced because of EDL at the channel walls. Electro-osmotic flow (EOF) is producing by presentation of electric field around the channel walls. The governing equations of total conservation of mass, momentum and thermal energy are:

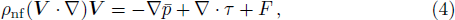
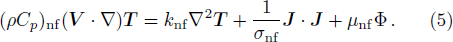
In describe model, V and T are the velocity temperature fields of nanofluid. As fluid flow is fully developed, therefore all the flow characteristics are independent of axial position. The net body force F that acting on fluid consists of mixed convection, magnetic and electrical effects. The mathematical expression of net body force can be written as:

The induced magnetic field is neglected for the small magnetic Reynolds number. The Joules heating effects generates due to Lorentz force and is Electrokinetic force produce due to particles charge surface form EDL. Here electric charge density is inside electrical double layer (EDL), and for a symmetric univalent dilute electrolyte it can be found as Ref. [38]. The electric field E is the external electric potential given by E = −▽Γ, Γ is electric potential define as a linear combination of the externally applied electric potential Ψ and EDL potential ψ, i.e., Γ = Ψ + ψ. Further, ψ and Ψ can be stated by the following equations:[39]

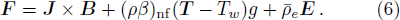
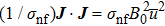
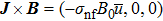
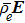
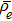
We assume that both walls of channel have different zeta potentials and made by different materials. The external electric field E = (Ex, 0, 0) is related to the applied electric field and total charge density of nanoparticles, which generates the electrical double layer. Electro-osmosis movement in the fluid is caused by electrical double layer. Equation (7), under the Debye-Huckel approximation can be written as:

where is termed as the Debye parameter, is the Debye length, with the different zeta potential at the walls

Equation (9) gives

The charge density becomes

The governing Eqs. (3) to Eq. (5) can be described in components form: Continuity:

Momentum:

Equation of energy with variable thermal conductivity:

The above set of equations are comprising the following boundary conditions

The correlation for dynamic viscosity of the nanofluid introduced by Maiga et al.[40] is

The nanofluid effective density is given by

The effective heat capability of the nanofluid is

The expression for thermal conductivity of nanofluid given by Maiga et al.[41] is

The electrical conductivity of nanofluid is

We dimensionless the governing equations via suitable similarity transforms given below

where κ is the electro-osmotic parameter and

is the Helmholtz-Smoluchowski velocity. By substituting the dimensionless variables deneded in Eq. (22) into Eqs. (13) and (15), we obtain:

Here it is supposed that the maximum velocity (um = −(a2/2μf) (∂p/∂x)) occurred between two walls, βu represents the ratio of Helmholtz-Smoluchowski electro-osmotic velocity to maximum velocity of nanofluid and consider γ is a dimensionless constant

Boundary conditions in dimensionless form

2.4 Shear Stress and Heat Flux

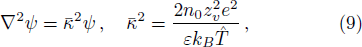
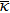
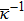
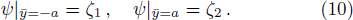
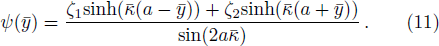
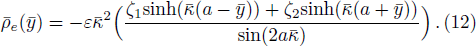
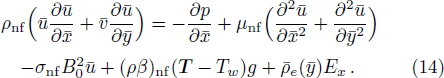
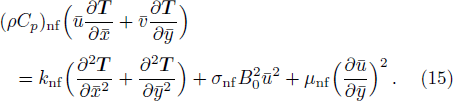
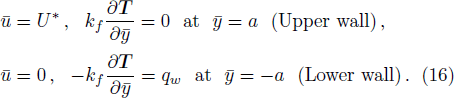
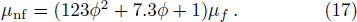
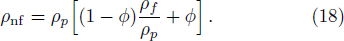
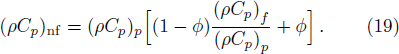
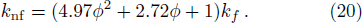
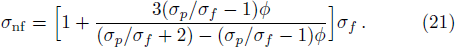
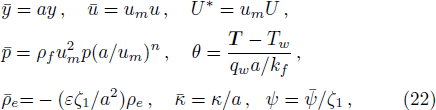
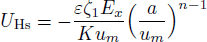
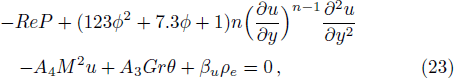
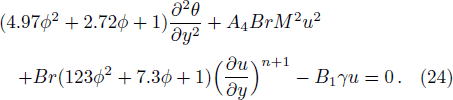
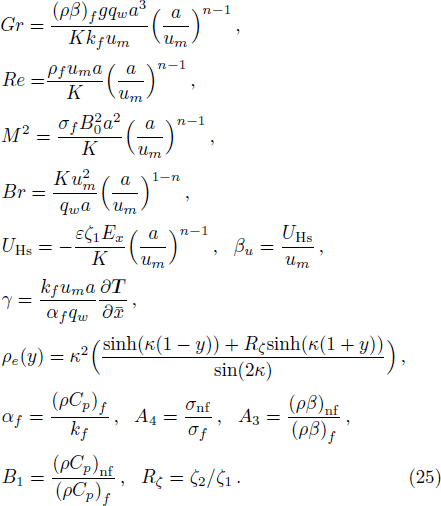
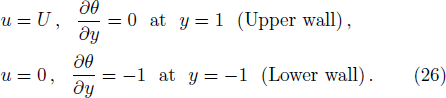
For non-Newtonian power-law fluid, shear stress can be calculated as:

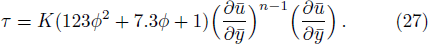
The different values of shear stress for polyvinyl alcohol at different concentration are discussed in Table 2.

Table 2

The properties of PVC solutions[37] and power-law equation.

.

The coefficient of skin-friction along the walls is

where τw the sharing stress at the walls is defined as:

At upper wall:

At lower wall:

The dimensionless skin-friction coefficient respectively at the upper and lower walls are:

For defining the Nusselt number, usually bulk mean fluid temperature Tm is used relatively as compare to the center line temperature in fully developed flow. Therefore the bulk mean temperature is defined as:

The mean temperature for dimensionless form can be obtained

The coefficient of heat transfer is defined as below:

Hence, the Nusselt number is defined as

3 Homotopy Solution of Problem

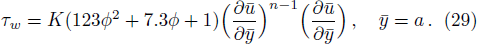
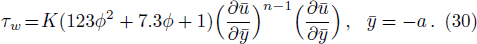
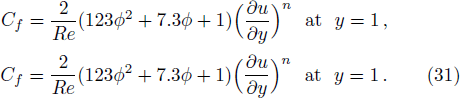
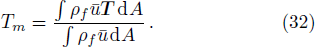
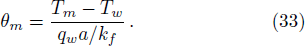
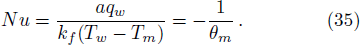
For analytical solution of Eqs. (23) and (24), we applied the analytical technique as proposed by Liao.[42] The initial approximations u0, θ0, which satisfies the boundary conditions given in Eq. (26).

We assume linear operators £1, £2 for series solutions are

We construct the homotopy for zero-th order deformation equations as:

here is embedding parameter with . For and , we write

ħu, ħθ, N1, and N2 are the non-zero auxiliary parameters and nonlinear operators for the velocity and temperature respectively. The nonlinear operators are

when embedding parameter diverges from 0 to 1, then velocity and temperature vary form initial approximation u0(y), θ0(y) to final u(y), θ(y) solution. By Taylor’s series expansion and Eq. (40) one can get

where

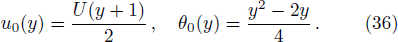
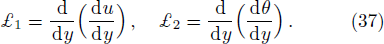
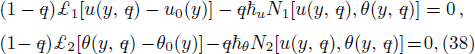
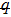
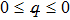
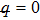
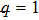
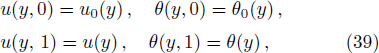
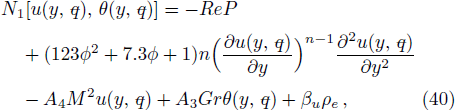
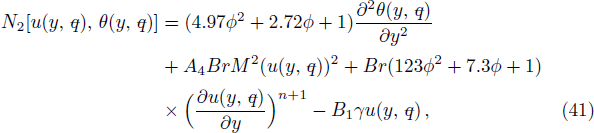
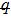
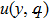
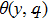
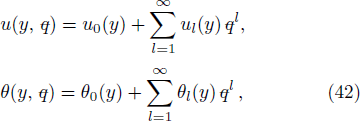
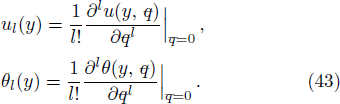
Estimate the results for ul(y) and θl(y) at l-th order deformation, as follow:

with

Linear ordinary differential equations are formed after l-th order deformation, which can be resolved easily by using symbolic computations software like: Matlab, Mupad, Mathematica, and Maple etc. In present study Mathematica is used to solve l-th order deformation equations up to 20-th order approximations. For the best understanding up to second order solutions for velocity and temperature distributions are expressed as:

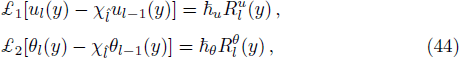
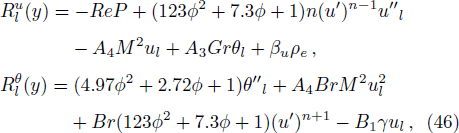
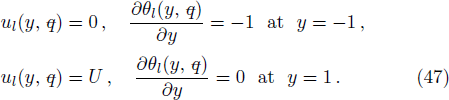
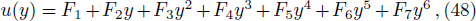
Coefficients F1, F2, F3, F4, F5, F6, F7, E1, E2, E3 are given in equations of Appendix A.

4 Convergence Analysis

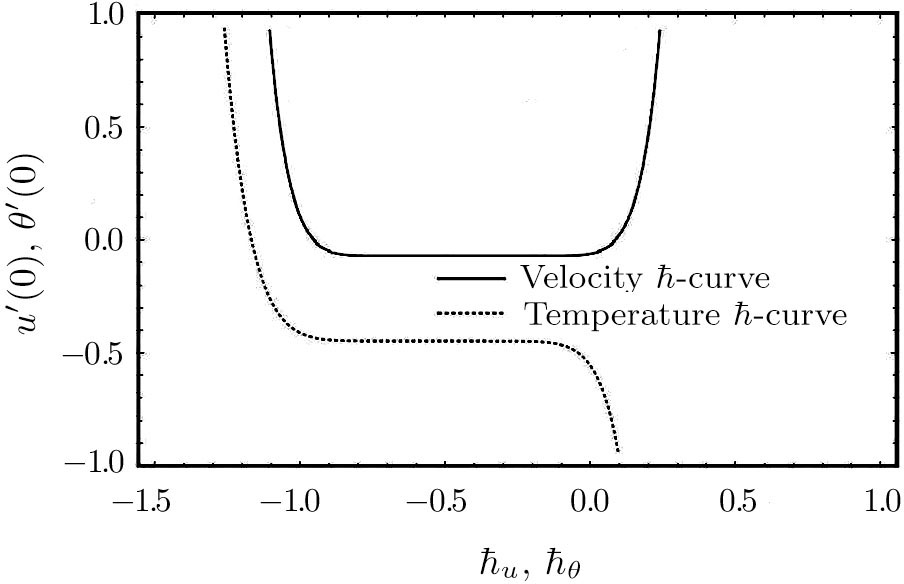The analytic expressions given by Eq. (43) contain the auxiliary parameters ħu and ħθ, which gives the convergence region and rate of approximation for HAM. Figure 2 depicts the ħ-curves for velocity and temperature and estimate the suitable values for interval of convergence. The range of estimated values of ħu for velocity and ħθ for temperature are −0.9 ≤ ħu ≤ 0 and −1.0 ≤ ħθ ≤ −0.1.

Fig. 2 ħ-curves for velocity and temperature. Gr = 2.366, Re = 442.956, n = 0.764(PVC3%), βu = 0.3, γ = 05, Br = 01, M = 0.5, κ = 10, and ϕ = 3%.

The residual error at two successive approximations over [0, 1] with homotopy analysis method by 20-th order approximations are obtained by using

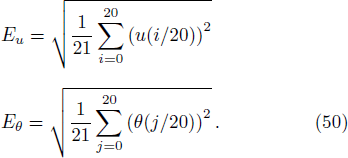
Equation (50) gives the minimum error at ħu = −0.1009 for velocity and ħθ = −0.2006 temperature profiles. Table 3 is exhibited to illustration the convergence of the solution with different order of approximation. The significant values of ħu and ħθ lie in their respective convergence range.

Table 3

Convergence of series solution when Gr = 2.366, βu = 0.3, γ = 05, Br = 01, Re = 442.956, n = 0.764(PVC3%), M = 0.5, κ = 10, and ϕ = 3%.

.
5 Results and Discussion

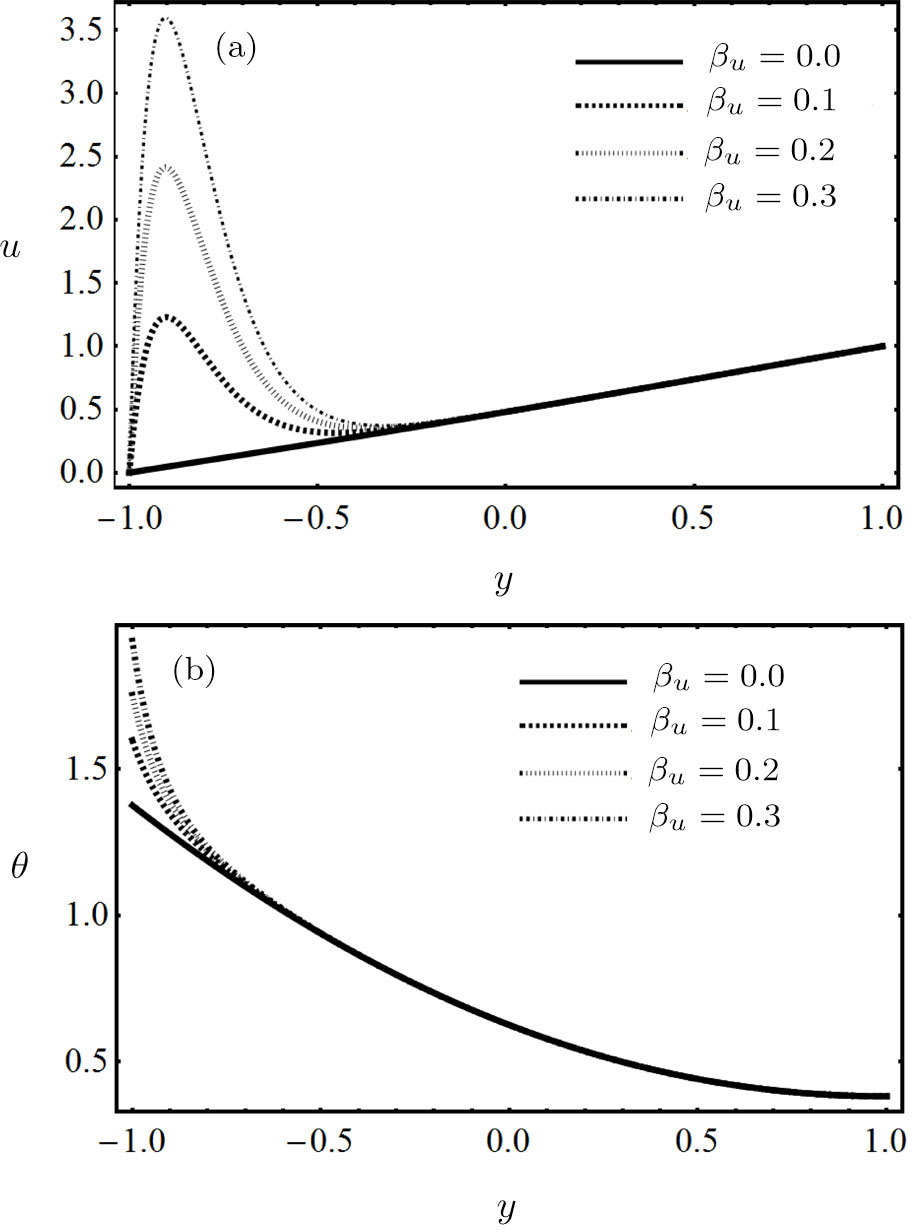
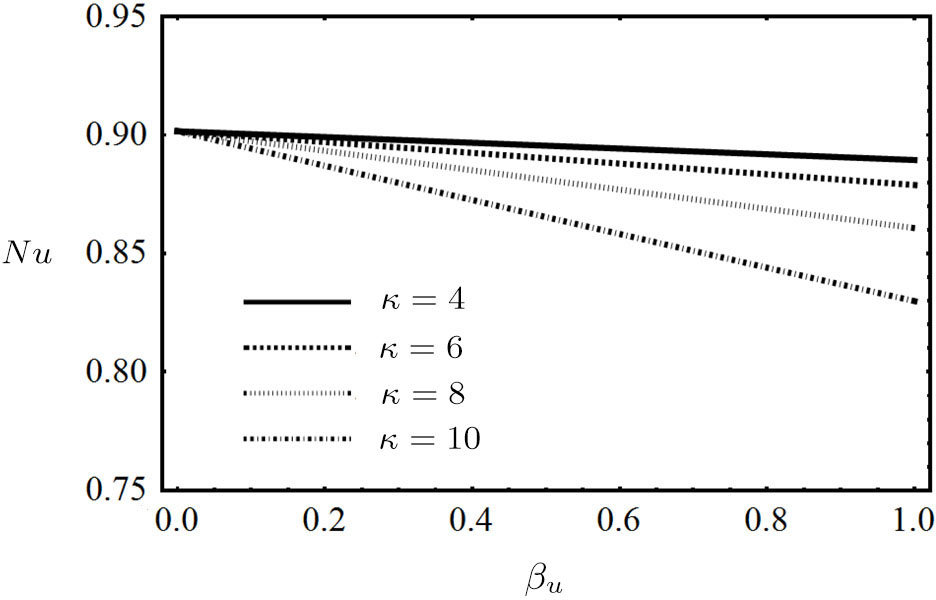
In present discussion, we study the Couette-Poiseuille non-Newtonian power-law nanofluid flow in between two parallel plates. The nanofluid is driven by the constant pressure gradient also with the axial movement of the upper plate and electric body force. Flow and heat transport of power-law nanofluid model among two parallel plates is examined analytically. Lower one is externally heated and upper one is adiabatic. The influence of electro-osmotic parameter, ratio of Helmholtz-Smoluchowski electro-osmotic velocity to maximum velocity, volume concentration of nanoparticles on flow field, modified magnetic parameter, modified Brinkman number and characteristic of heat transfer are elaborated through graphically in Figs. 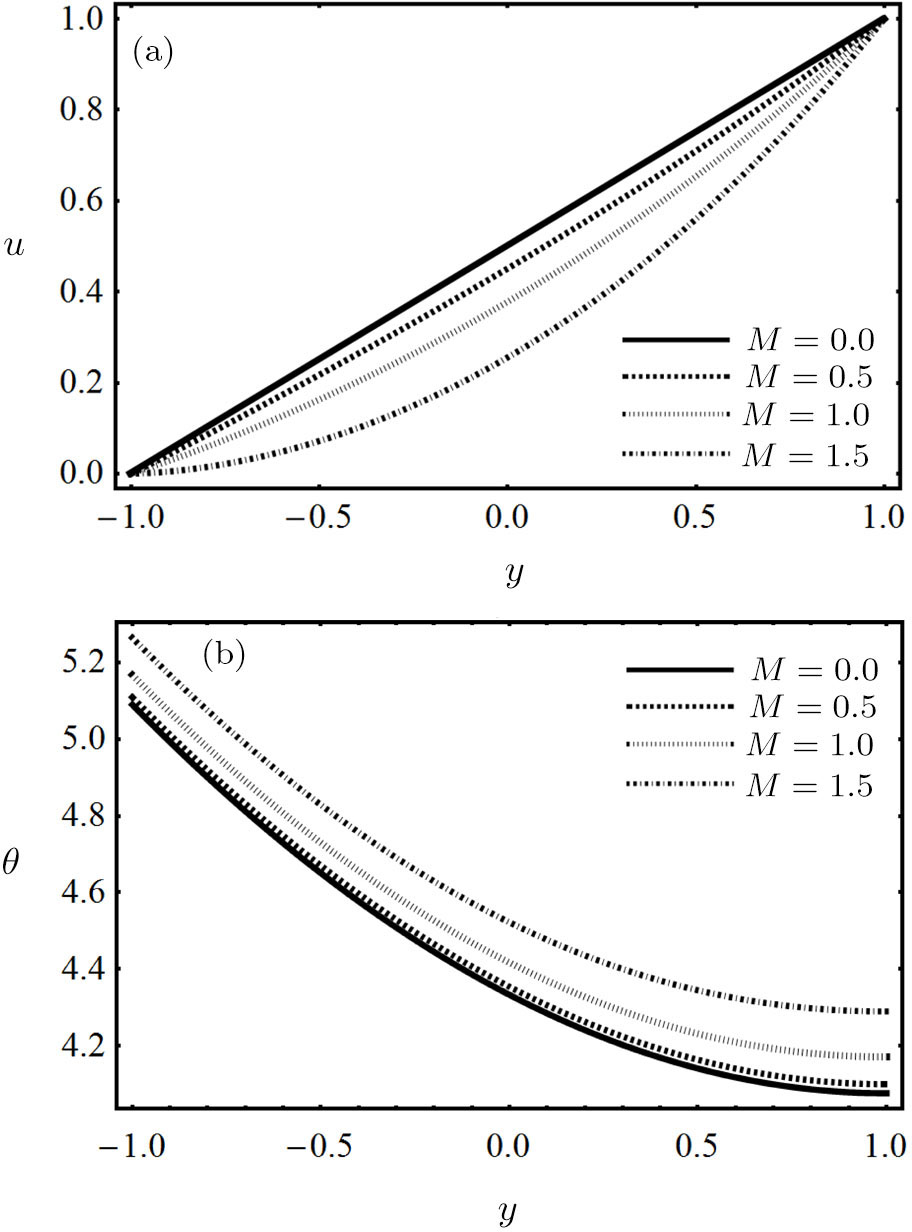3–10. The following discussion and results are obtained by using appropriate values of emerging parameters: Gr = 2.366, Re = 442.956, n = 0.764(PVC3%), ϕ = 0.03, M = 2, βu = 0.3, γ = 10, κ = 8, U = 1, and Br = 1.

Fig. 3 (a) Impact of magnetic parameter on fluid velocity. (b) Impact of magnetic parameter on fluid temperature.

The effects of modified magnetic parameter M on velocity and temperature distribution of nanofluid are displayed in Fig. 3. From these plots, it is investigated that the velocity and temperature are decelerate and accelerate in Figs. 3(a) and 3(b) respectively when the magnetic parameter increased. As the transverse magnetic field applied on the electrically conducted nanofluid normal to the flow direction, then it creates a drag force called Lorentz force in the opposite direction of flow. This drag force increases the strength of magnetic field and as a result this increment resist the fluid flow, therefore velocity of fluid decreased while the temperature of fluid increased. Impact of nanoparticles volume fraction ϕ for velocity and temperature are exposed in Fig. 4. It can observe from Fig. 4(a), velocity between the channel walls is reducing as compared to the pure fluid (ϕ = 0%). It is due to when the nanoparticles substitute in carrier fluid then the density of the carrier fluid increases, therefor nanofluid becomes denser, so this substitution of nanoparticles in carrier fluid slow down the movement of nanofluid. Temperature of nanofluid accelerate with the increase of nanoparticles volume fraction as shown in Fig. 4(b). Physically, thermal conductivity of nanofluid increased with the increase of nanoparticles volume fraction.

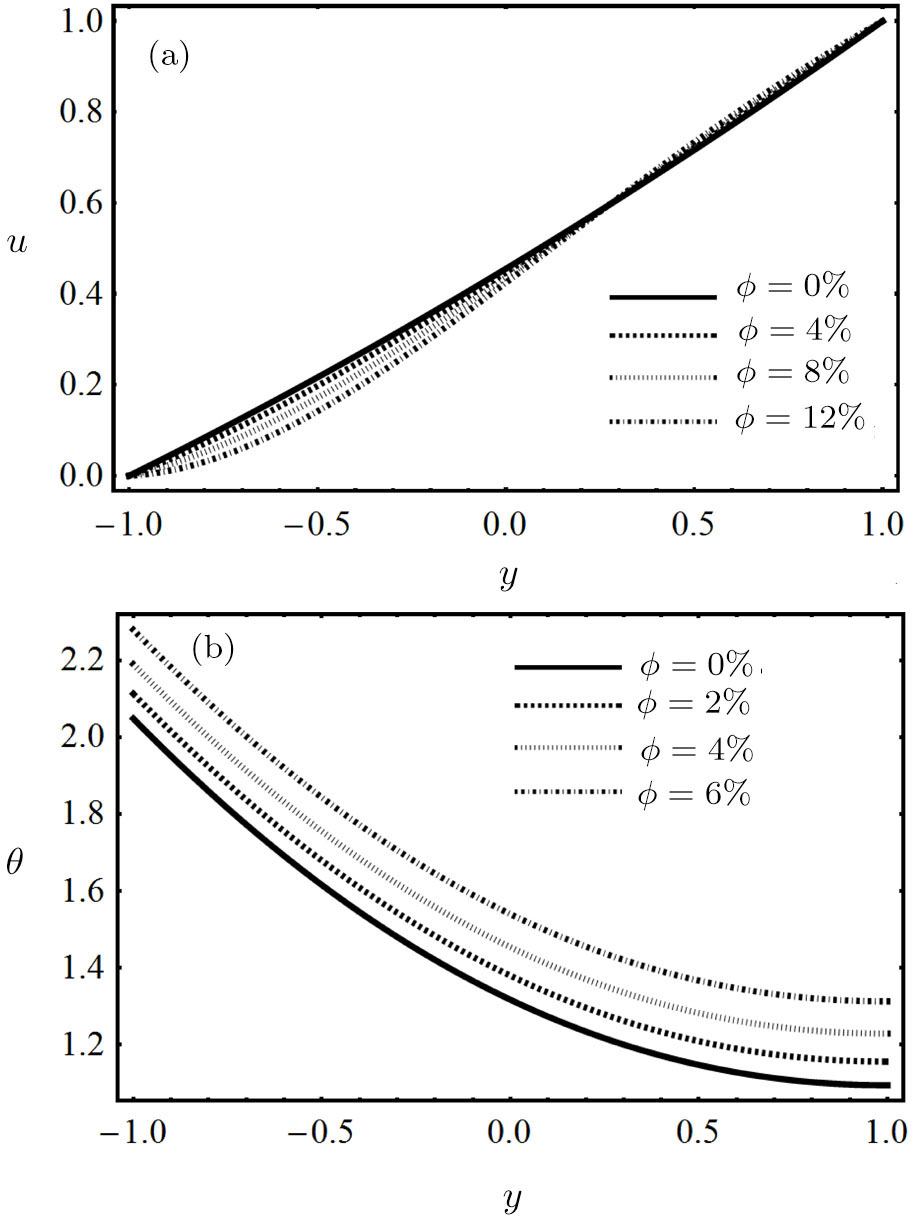Fig. 4 (a) Impact of nanoparticle volume fraction on fluid velocity. (b) Impact of nanoparticle volume fraction on fluid temperature.

Different concentrations of PVC on the flow field and temperature field of nanofluid are elaborates in Fig. 5. From Fig. 5(a), it is noted that the velocity profile of nanofluid enhanced when the concentration of PVC in fluid increased. The temperature profile for different concentrations of PVC is elaborate in Fig. 5(b). From this plot it can clearly be detected that the decrement in temperature is occurred between the walls of channel. As the βu represents the ratio of Helmholtz-Smoluchowski electro-osmotic velocity to maximum velocity of nanofluid. The effects of this ratio displayed for nanofluid flow and thermal distribution in Fig. 6. It can clearly observe in Fig. 6(a) that an increment in Helmholtz-Smoluchowski electro-osmotic velocity as compared to maximum velocity, the flow of nanofluid near the heated wall overshoot and reaches its maximum value at the wall of the channel. It is further seen that up to a certain height of the channel there is no signicant changes in the fluid velocity with increase in βu. Whereas, increase in electro-osmotic velocity little bit change occurs in temperature distribution at the heated wall as shown in Fig. 6(b). Impact of electro-osmotic parameter κ on the fluid flow and temperature profile is exposed in Fig. 7. It can be observed in Fig. 7(a) for larger value of κ will increase the fluid flow. This is because that the velocity profiles for bigger κ will exhibit thinner EDL layers and consequently larger velocity gradients. The influence of κ on dimensionless temperature profile in the absence of Joule heating is examined in Fig. 7(b). It is noted that for pseudo-plastic (shear-thinning fluid i.e. n<1) an increase in dimensionless electro-osmotic parameter κ is accompanied by an increase in dimensionless temperature distribution.

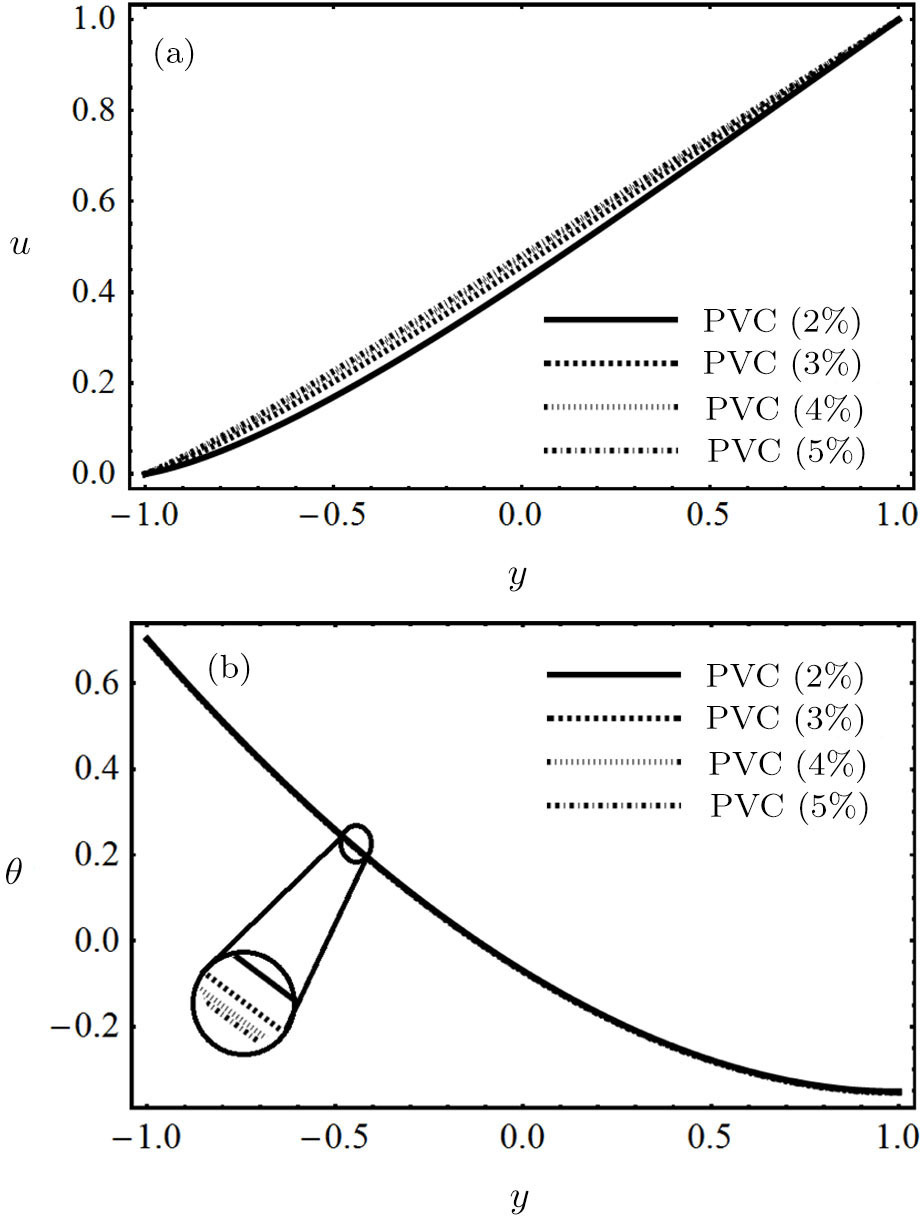Fig. 5 (a) Impact of PVC concentration on fluid velocity. (b) Impact of PVC concentration on fluid temperature.
Fig. 6 (a) Impact of βu on fluid velocity. (b) Impact of βu on fluid temperature.
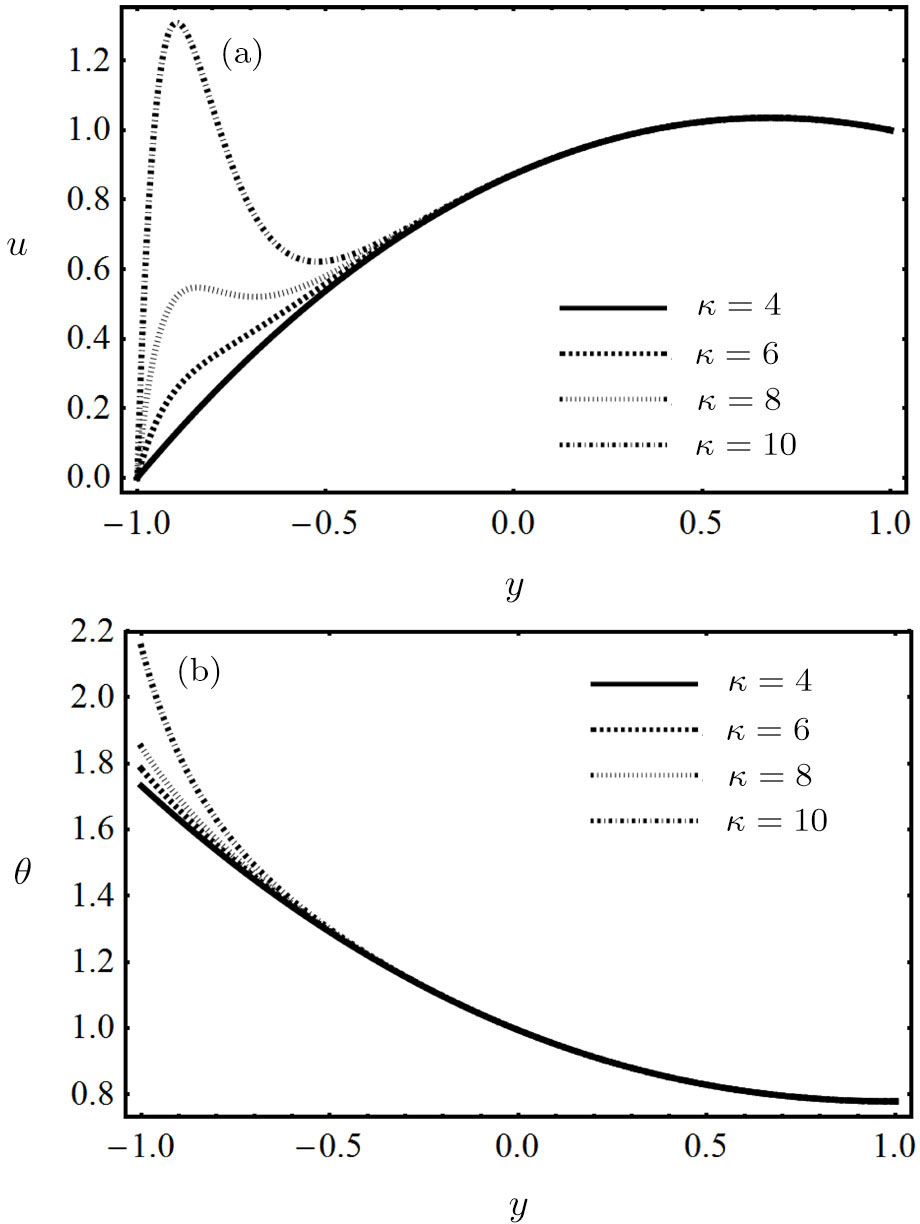Fig. 7 (a) Impact of electro-osmotic parameter on fluid velocity. (b) Impact of electro-osmotic parameter on fluid temperature.

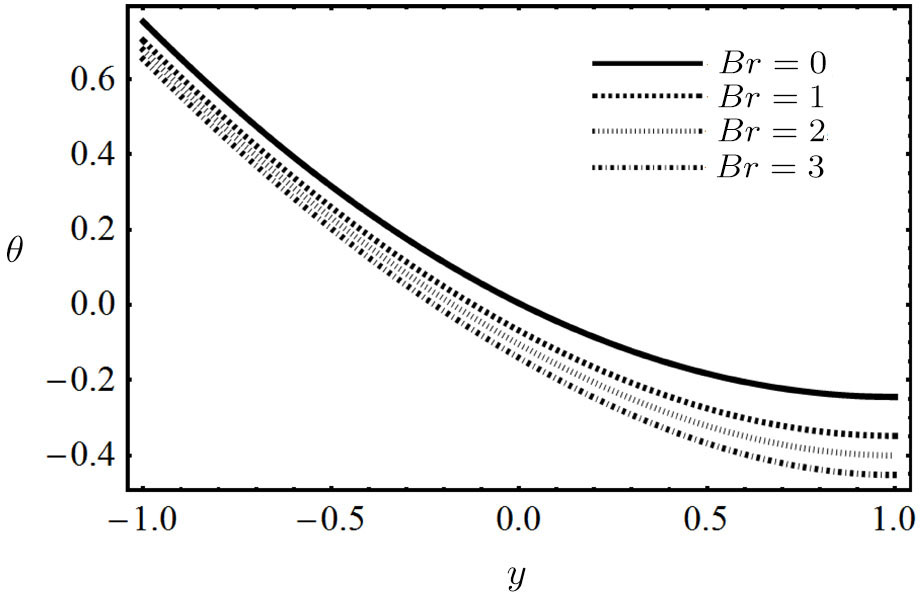
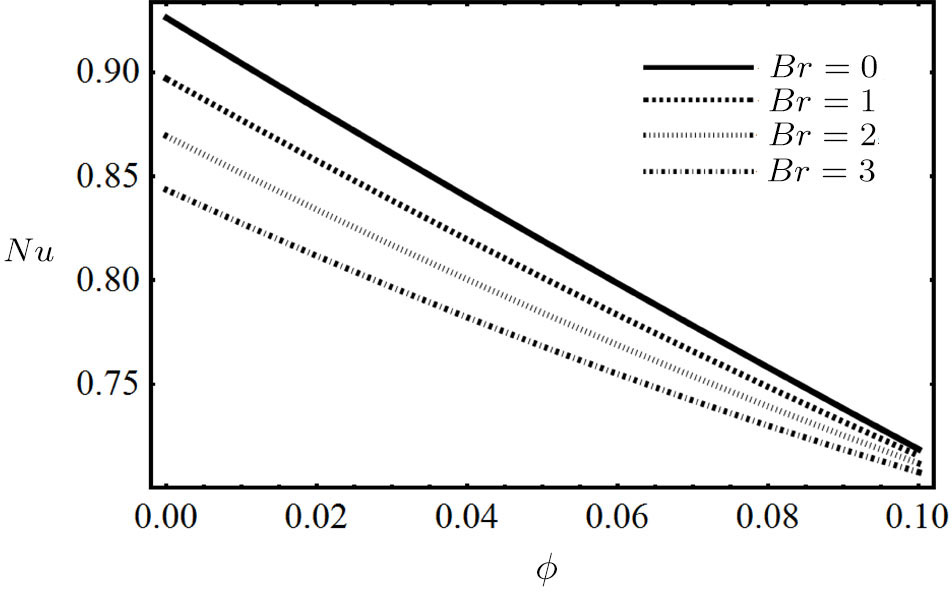
The influence of modified Brinkman number Br and γ constant on the temperature is shown in Fig. 8. It is cleared from Fig. 8, for the increasing values of modified Brinkman number, the curves of energy profile drop down, which infers that Br rises the wall temperature as compare to bulk mean temperature. This is due to fact that fewer energy is transported adjacent to the walls by the fluid flow rather than the core area, which is fallouts of higher values of temperature near the wall area.

Fig. 8 Impact of Brinkman number Br on fluid temperature.

Increasing effects on Nusselt number due to increase of nanoparticles volume fraction and modified Brinkman number are shown in Fig. 9. Results show that there is enhancement in temperature field θm for larger values of nanoparticle volume fraction. The impact of Nusselt number w.r.t the ratio of Helmholtz-Smoluchowski electro-osmotic velocity to maximum velocity of nanofluid βu and electro-osmotic parameter κ portray in Fig. 10. It is inspiring to observe that the Nusselt number decreases in the fluid layer closer to the heated wall. The reason is that, heat is shifted from the heated plate to the fluid and from the fluid to the isolated plate. Table 4 represents the numerical results of modified Brinkman number, volume concentration of nanoparticles on flow field, modified magnetic field parameter, ratio of Helmholtz-Smoluchowski electro-osmotic velocity to maximum velocity and electro-osmotic parameter on skin friction coefficient. Result noted that the Skin friction at moving isolated wall decreases with the increase of modified magnetic parameter and modified Brinkman number, while increases with the increase of electro-osmotic parameter and ratio of Helmholtz-Smoluchowski electro-osmotic velocity to maximum velocity.

Fig. 9 Impact of Br w.r.t ϕ on Nusselt number.
Fig. 10 Impact of κ w.r.t βu on Nusselt number.
Table 4

Skin friction coefficient Cf for several of Br, ϕ, M, βu and κ with n = 0.764(PVC3%) at both walls.

.
6 Conclusions

The present communication addresses the Couette-Poiseuille power law Al2O3-PVC nanofluid flow between two parallel plates, in which upper plate is moving with constant velocity. The influences of magnetic field, mixed convection and electrical double layer (EDL) are incorporated in momentum transfer. The energy distribution along with the joule heating and viscous dissipation are also considered. The velocity of the nanofluid is generated due to constant pressure gradient in axial direction. The flow problem is first modeled and then transformed into dimensionless form via appropriate similarity transformation. Homotopy analysis method (HAM) is utilized to tackle the resulting dimensionless flow problem. The impact of sundry parameters on fluid velocity, temperature distribution, skin friction coefficient and Nusselt number are expressed for shear-thinning nanofluid through figures. The key outcomes of the problem can be comprehended as follows:

It is perceived that the velocity of nanofluid decelerate by increasing the values of modified magnetic parameter and nanoparticles volume fraction, whereas the temperature profile is increased by increasing the said parameters.

The velocity of non-Newtonian power-law nanofluid enhanced as concentration of PVC rise up, while opposite trend shows for temperature distribution.

The flow and temperature are the same enlarged behavior for increasing the ratio of Helmholtz-Smoluchowski electro-osmotic velocity to maximum velocity and electro-osmotic parameter.

Skin friction at externally heated wall increases with the increase of nanoparticles volume fraction and modified Brinkman number, while decreases with the increase of modified magnetic parameter, electro-osmotic parameter and ratio of Helmholtz-Smoluchowski electro-osmotic velocity to maximum velocity.

Skin friction at moving isolated wall decreases with the increase of modified magnetic parameter, nanoparticles volume fraction and modified Brinkman number, while increases with the increase of electro-osmotic parameter and ratio of Helmholtz-Smoluchowski electro-osmotic velocity to maximum velocity.

Nusselt number at heated wall decreases with the increase of electro-osmotic parameter, ratio of Helmholtz-Smoluchowski electro-osmotic velocity to maximum velocity, nanoparticles volume fraction and modified Brinkman number, while increases with the increase of modified magnetic parameter.

Reference
[1] Choi S. U. S. Enhancing Thermal Conductivity of Fluids with Nanoparticles Siginer D. A. Wang H. P. Developments and Applications of Non-Newtonian Flows ASME New York 66 1995 99
[2] Pak B. C. Cho Y. I. Exp. Heat. Transf. 11 1998 151
[3] Xuan Y. Li Q. Int. J. Heat Fluid Fl. 21 2000 58
[4] Bhatti M. M. Zeeshan A. Ellahi R. Microvascular Res. 110 2017 32
[5] Shehzad N. Zeeshan A. Ellahi R. Vafai K. J. Mol. Liq. 222 2016 446
[6] Rashidi S. Esfahani J. A. Ellahi R. Appl. Sci. 7 2017 431
[7] Hassan M. Zeeshan A. Majeed A. Ellahi R. J. Magn. Magn. Mater 443 2017 36
[8] Rashidi S. Akar S. Bovand M. Ellahi R. Renew. Energ. 115 2018 400
[9] Ijaz N. Zeeshan A. Bhatti M. M. Ellahi R. J. Mol. Liq. 250 2018 80
[10] Tripathi D. Sharma A. Beg O. A. Int. J. Heat Mass Transf. 111 2017 138
[11] Irvine T. F. Karni J. Non-Newtonian Fluid Flow, Handbook of Single-Phase Convective Heat Transfer 1987 20
[12] Chhabra R. P. Richardson J. F. Non-Newtonian Flows in the Process Industries: Fundamentals and Engineering Applications Butterworth-Heingmann 1 1999
[13] Reuss F. F. Memoires de la Societe Imperiale des Naturalistes de Moscou. 2 1809 327
[14] Probstein R. F. Renaud P. C. Quantification of Fluid and Chemical Flow in Electrokinetics Seattle, Wash. 1986 4
[15] Zeeshan A. Bhatti M. M. Akbar N. S. Sajjad Y. Commun. Theor. Phys. 68 2017 103
[16] Tripathi D. Sharma A. Beg O. A. Tiwari A. J. Therm Sci. Eng Appl. 9 2017 410
[17] Tripathi D. Jhorar R. Beg O. A. Kadir A. J. Mol Liq. 236 2017 358
[18] Tripathi D. Yadav A. Beg O. A. Eur Phys. J. Plus. 132 2017 173
[19] Prakash J. Sharma A. Tripathi D. J. Mol. Liq. 249 2018 843
[20] Viskanta R. The 6th International Symposium on Tragnsport Phenomena in Thermal Enaineering Seoul, Korea 1992
[21] Kang B. H. Jaluria Y. J. Thermophys. Heat Tr. 8 1994 546
[22] Shah R. K. Londan A. L. Laminar Flow Forced Convection in Ducts: A Source Took for Compact Heat Exchanger Analytical Data Academic Press New York 2014
[23] Hudson J. L. Bankoff S. G. Chem. Eng. Sci. 20 1965 415
[24] Sestak J. Rieger F. Int. J. Heat Mass Transf. 12 1969 71
[25] Bruin S. Int. J. Heat Mass Transf. 15 1972 341
[26] Davis E. J. Can. J. Chem. Eng. 51 1973 562
[27] El-Ariny A. Aziz A. ASME J. Heat Transf. 98 1976 427
[28] Davaa G. Shigechi T. Momoki S. Int. Commun. Heat Mass. 31 2004 663
[29] Hayat T. Khan M. Asghar S. Acta Mech. 168 2004 213
[30] Hashemabadi S. H. Etemad S.G. Thibault J. Int. J. Heat Mass Transf. 47 2004 3985
[31] Marin M. Meccanica. 51 2016 1127
[32] Rashidi S. Esfahani J. A. Valipour S. M. Bovand M. Pop I. lnt. J. Numer. Method H. 26 2016 1416
[33] Tripathi D. J. Int. Acad. Chys. Sci. 19 2017 245
[34] Ellahi R. Rahmsn S. U. Nadeem S. Vafai K. Commun. Theor. Phys. 63 2015 353
[35] Maqbool K. Slhaio A. Manzoor N. Ellahi R. Commun. Theor. Phys. 66 2016 547
[36] Ellahi R. Bhatti M. M. Fetecau C. Vafai K. Commun. Theor. Phys. 65 2016 66
[37] Ellahi R. Hassan M. Zeeshan A. Therm Sci. 20 2016 2015
[38] Probstein R. F. Physicochemical Hdyrodynamics: An Introduction John Wiley & Sons New York 1974
[39] Wang X. Qi H. Yu B. et al. Commun. Nonlinear Sci. 50 2017 77
[40] Maiga S. E. B. Palm S. J. Nguyen C. T. et al. Int. J. Heat Fluid Fl. 26 2005 530
[41] Maiga S. E. B. Tam N. C. Galanis N. et al. Int. J. Numer Method Heat Fluid Fl. 16 2006 9
[42] Liao S. J. The Proposed Homotopy Analysis Technique for the Solution of Nonlinear, Problems Ph. D Thesis Shanghai Jiao Tong University Shanghai 1992