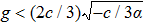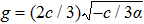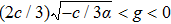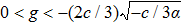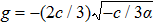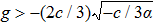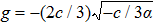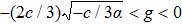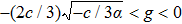The Fujimoto-Watanabe equation

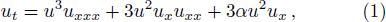
In this section, we present the bifurcations of phase portraits corresponding to Eq. (1).

Substituting u(x,t) = φ(ξ) with ξ = x − ct into Eq. (1), it follows,

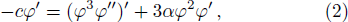
Integrating straightforwardly Eq. (2), we get

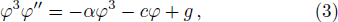
Letting y = φ′, we obtain a three-parameter planar system

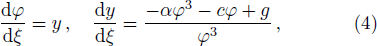
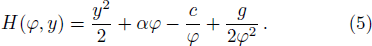
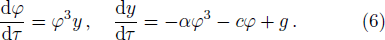
System (6) has the same level curves as system (4). Therefore, we can analyze the phase portraits of system (4) from those of system (6).

To study the singular points and their properties of system (6), let

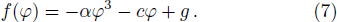
We can easily obtain the graphics of the function f(φ) in Figs. 1 and 2 under corresponding parameters conditions.^[13]

Fig. 1

	Figure Option ViewDownloadNew Window
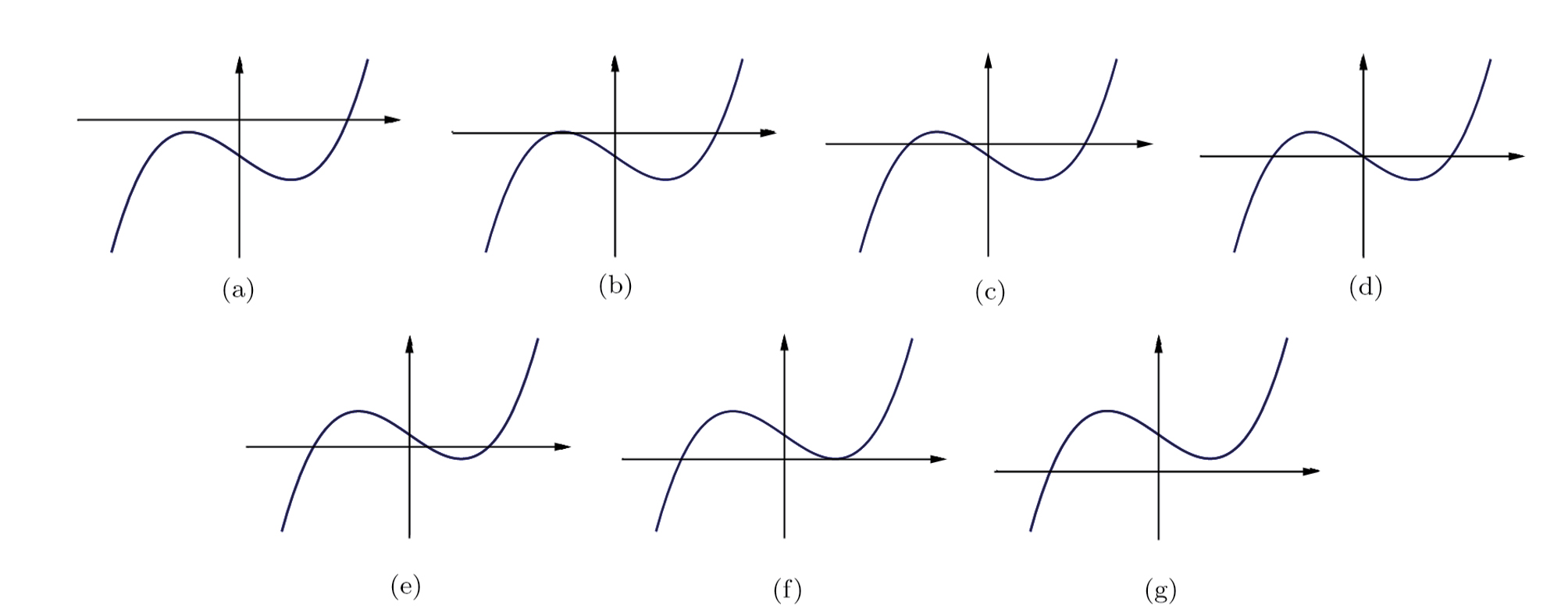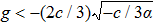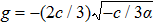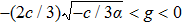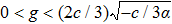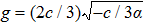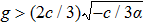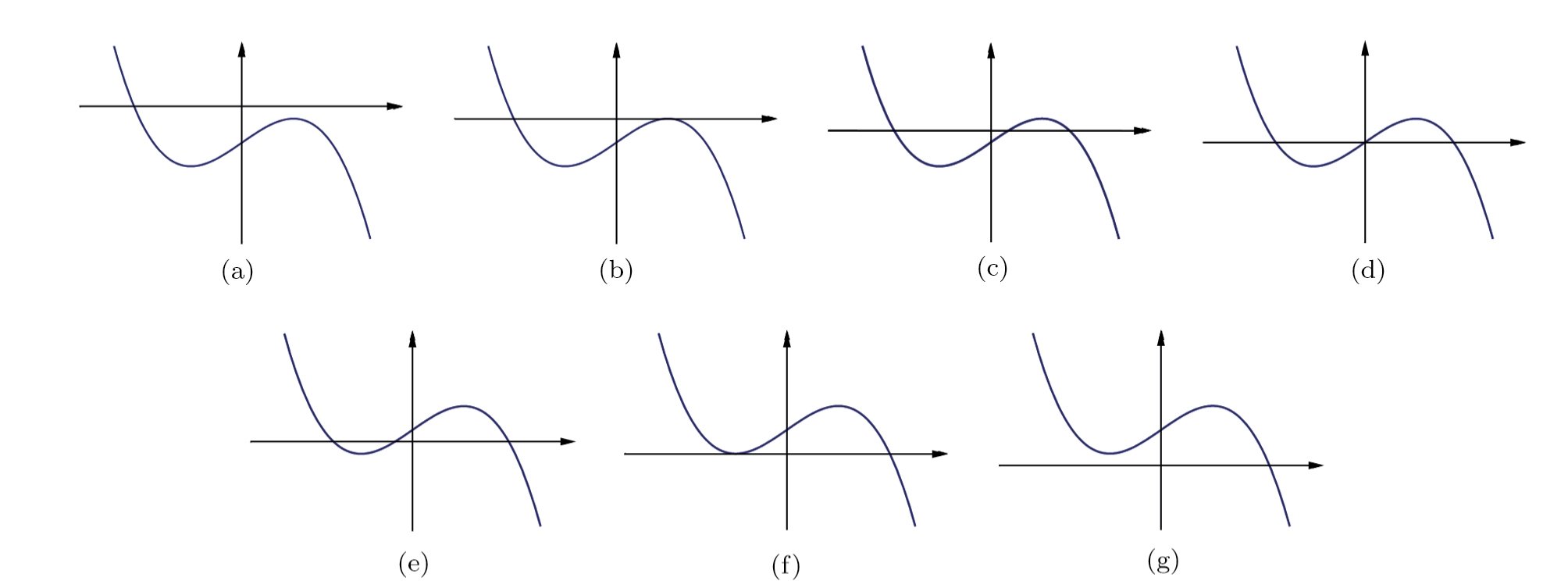	Fig. 1 The graphics of the function f(φ) when α < 0 and c > 0. (a) , (b) , (c) , (d) g = 0, (e) , (f) , (g) .

Fig. 2

	Figure Option ViewDownloadNew Window
	Fig. 2 The graphics of the function f(φ) when α > 0 and c < 0. (a) 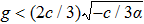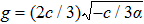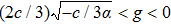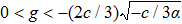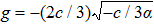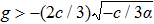, (b) , (c) , (d) g = 0, (e) , (f) , (g) .

Let λ(φ*,y) be the characteristic value of the linearized system of system (6) at the singular point (φ*,y). We have

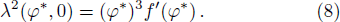
From Eq. (8), we see that the sign of f′(φ*) and the relative position of the singular point (φ*,0) with respect to the singular line l : φ = 0 can determine the dynamical properties (saddle, center, and degenerate singular point) of the singular point (φ*,0) according to the theory of planar dynamical systems.

We summarize the number, relative positions and dynamical properties of singular points of system (6) when α < 0 and c > 0 in the following lemma. Here we just omit these informations for the other case when α > 0 and c < 0 for convenience.

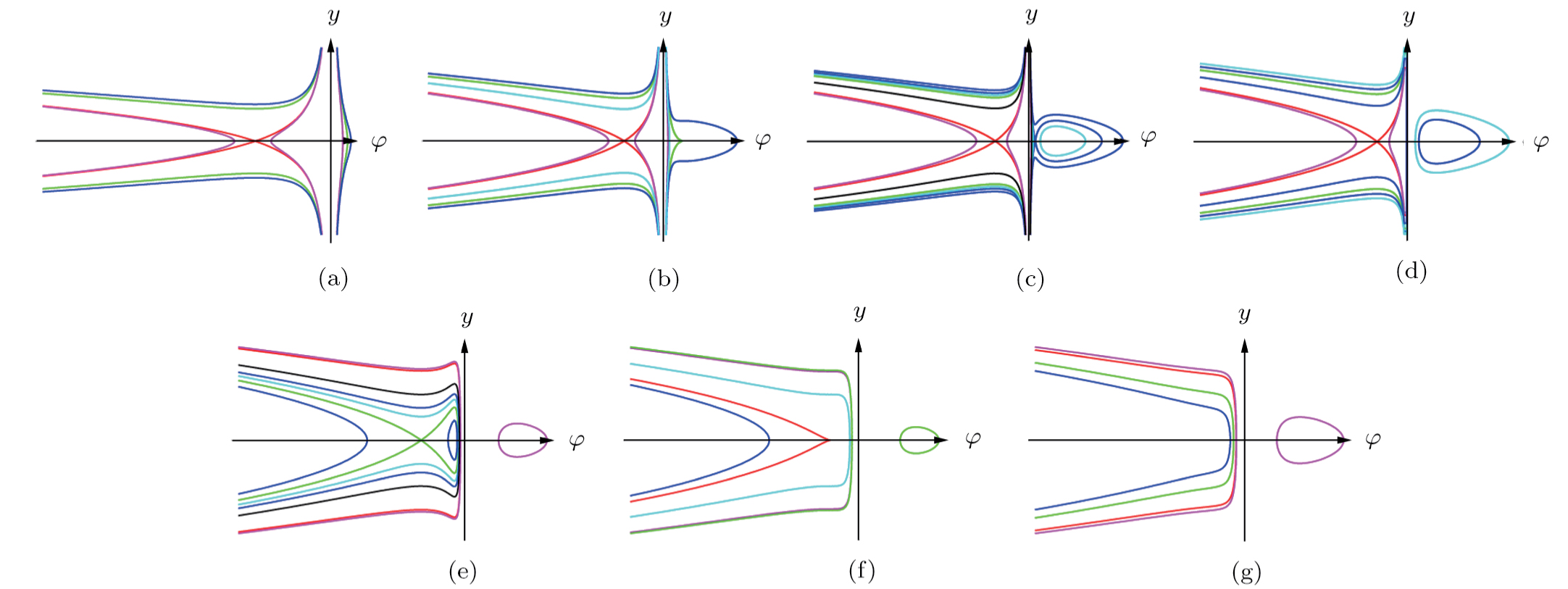
Therefore, based on the above analysis, we obtain all possible phase portraits of bifurcations of system (4) in Figs. 3 and 4.

Fig. 3

	Figure Option ViewDownloadNew Window
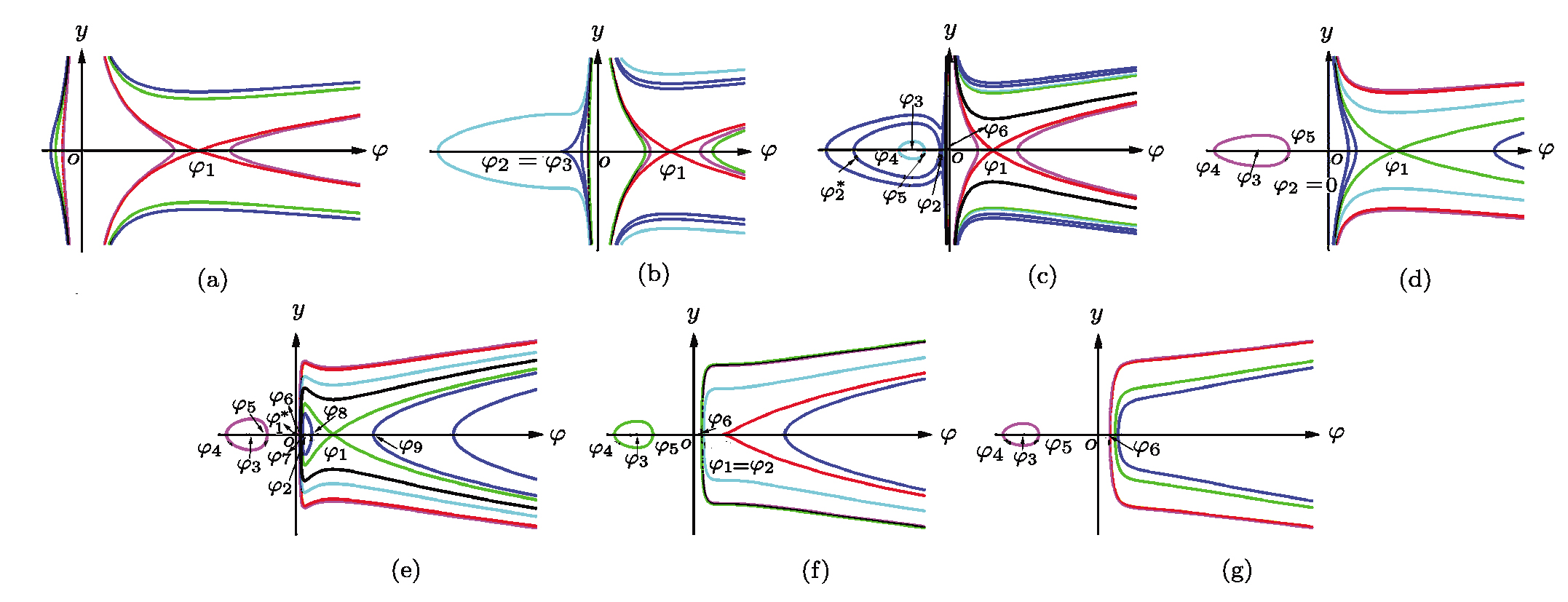	Fig. 3 The phase portraits of system (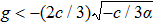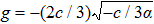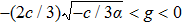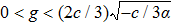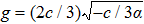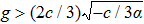4) when α < 0 and c > 0. (a) , (b) , (c) , (d) g = 0, (e) , (f) , (g) .

Fig. 4

	Figure Option ViewDownloadNew Window
	Fig. 4 The phase portraits of system (4) when α > 0 and c < 0. (a) , (b) , (c) , (d) g = 0, (e) , (f) , (g) .

To state conveniently, we introduce some marks,

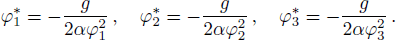
Our main results will be stated in the following theorem, and the proof follows. Note that we only focus our attention on the case when α < 0 and c > 0 about the main results, because the other case when α > 0 and c < 0 can be considered similarly.

Fig. 5

	Figure Option ViewDownloadNew Window
	Fig. 5 The compactons, kink-like, and antikink-like wave solutions to Eq. (1). (a) , (b) , (c) .

Fig. 6

	Figure Option ViewDownloadNew Window
	Fig. 6 The graphics of the kink-like and antikink-like wave solutions Eq. (14). (a) Kink-like wave solution, (b) Antikink-like wave solution.

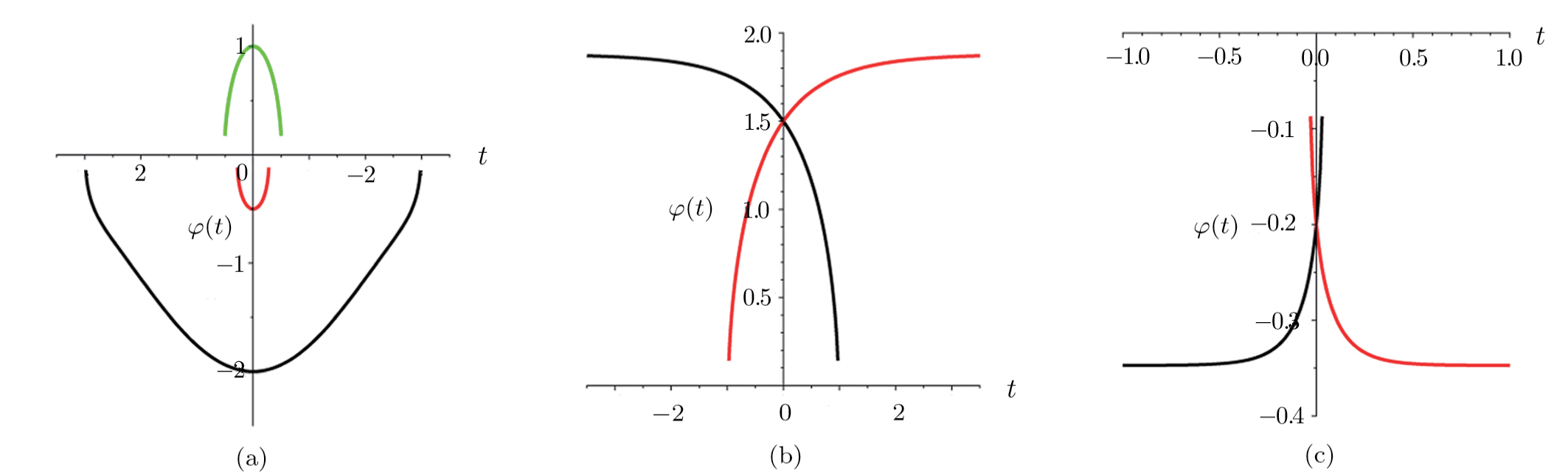
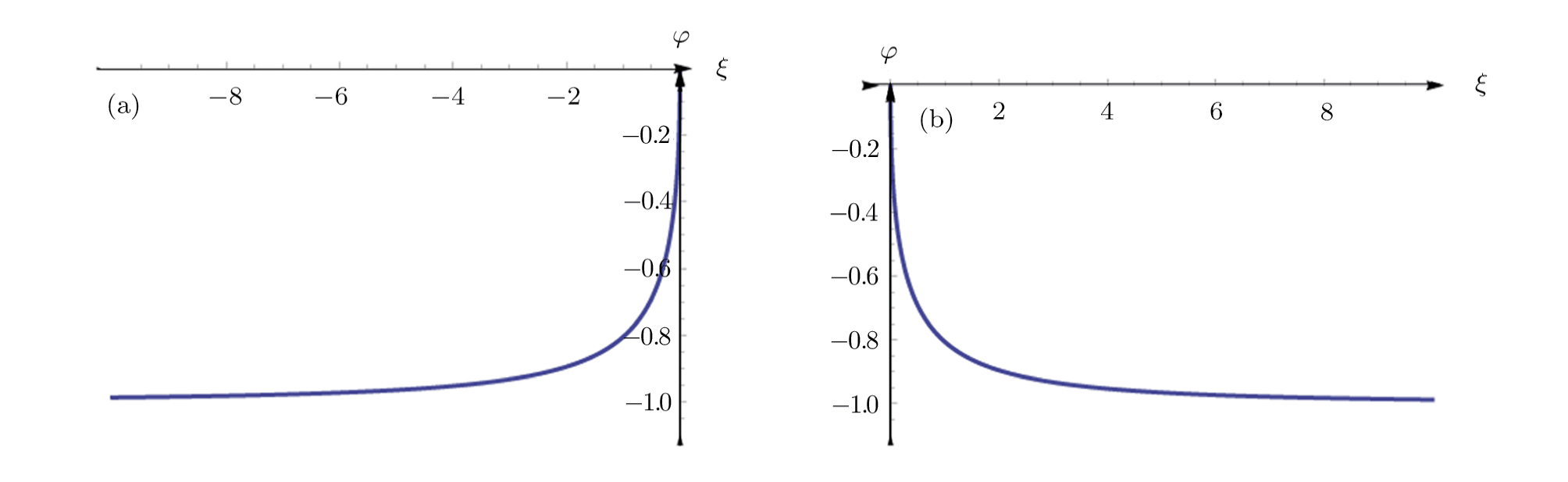
In this paper, through all possible bifurcations for the system under different parameters conditions, we show the existence and dymanics of traveling wave solutions including solitary wave solutions, periodic wave solutions, compactons and kink-like and antikink-like wave solutions. Moreover, the expressions of solitary wave solutions and periodic wave solutions are implicitly given, while the expressions of kink-like and antikink-like wave solutions are explicitly shown. The dynamics of these new traveling wave solutions will greatly enrich the previews results and further help us understand the physical structures and analyze the propagation of the nonlinear wave.