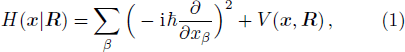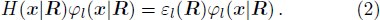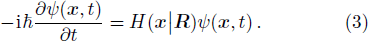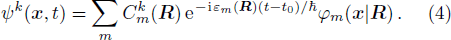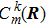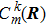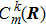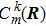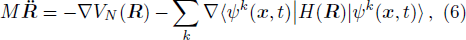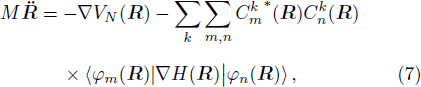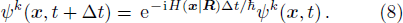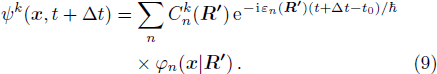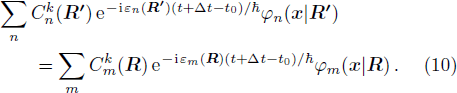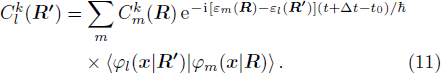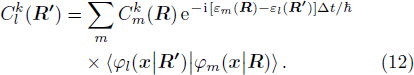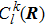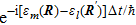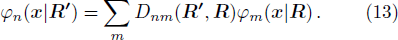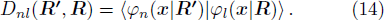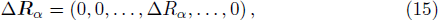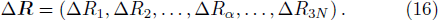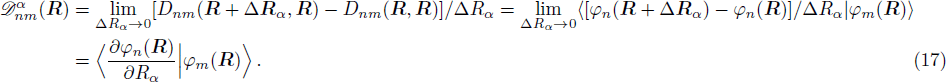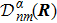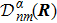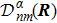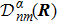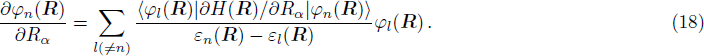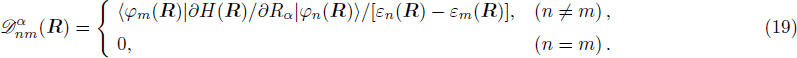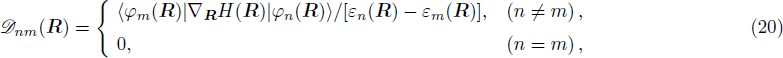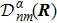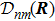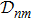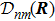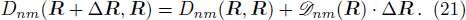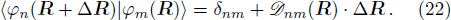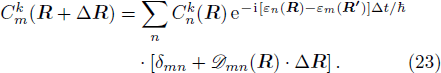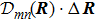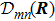1 IntroductionIn molecule, since nuclei are much heavier than electrons, they are considered as classical particle, this is semi-quantum molecular dynamics. The electronic states in molecule are time-dependent superpositions of all the eigenstates, and the electron distribution is changing with the time, this is dynamical evolution. At the same time, the nuclear motion makes the base vectors of the eigenstates continuously varying, and it indirectly induces additional evolution, it is kinematical evolution.
Recent years, the semi-quantum molecular dynamics, especially the Ehrenfest dynamics, have got further progress,[1–4] where the dynamical evolution can be expressed analytically, and its calculation is transparent. However, the kinematical one depends on complicated numerical calculation,[5–7] which causes some confusions. It is needed to establish an analytic formula to express the kinematical evolution, then all the results become definite. This paper will provide one approach based on the connection in the geometry to derive such an expression.
A molecule consists of N nuclei and M electrons, the coordinates of nuclei are {R} = (R1 ⋯ Rα ⋯ R3N) and that of electrons are x = (x1 ⋯ xβ ⋯ x3M). R determines the configuration and shape of the molecule.
The electronic Hamiltonian is
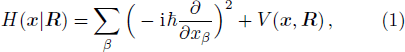
where
V(
x,
R) is the interaction between electrons and nuclei. In
H(
x|
R),
R are parameters, the eigen-equation of
H(
x|
R) is
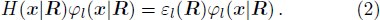
The eigen-functions
φl(
x |
R) constitute an orthogonal complete set, which can serve as the base vectors of a Hilbert space.
2 FormulationThe time-dependent Schrödinger equation is
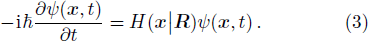
At any moment
t, the molecule has a definite configuration
R and corresponding complete set of
φm(
x |
R), the electronic state
ψk(
x,
t) (
k is the number of the state) can be expanded by
φm(
x |
R)
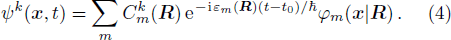
Actually Eq. (4) is the solution of Schrödinger Eq. (3). Here 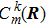 , which depends only on R, is the component of the electronic state ψk(x, t) in the Hilbert space. In other words,
, which depends only on R, is the component of the electronic state ψk(x, t) in the Hilbert space. In other words, 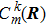 is the electronic state in φn representation. When molecular configuration R changes slowly, the base vectors φm(x | R) follow to vary, and the electronic state
is the electronic state in φn representation. When molecular configuration R changes slowly, the base vectors φm(x | R) follow to vary, and the electronic state 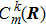 evolves.
evolves.
At the beginning t = t0, R = R0, if an electron stays in the eigen-function φl(x | R0), i.e.

Afterward, the electronic state will spread over all the eigenstates. If imposing
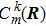
always to be
δm,l, it is BOA (Bohn-Oppenheimer Approximation).
Nuclei obey the Newtonian equation
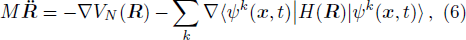
where
VN(
R) is the interaction among nuclei.
By using the generalized Hellmann-Feynman Theorem,[8] Eq. (6) can be simplified to
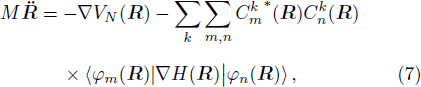
the gradient matrix ⟨
φm(
R)|∇
H(
R)|
φn(
R)⟩ is easy to get by numerical calculation, it is the key factor to solve the Newtonian Eq. (
7). Later, it can be seen that the gradient matrix will play an important part also in solving Schrödinger equation.
By solving the combined equations of Schrödinger Eq. (3) and Newtonian Eq. (7), both the electronic states Cm(R) and nuclear motion R(t) can be obtained. Since nuclear motion is much slower than that of electrons, a practical method to solve these combined equations is the iteration approach step by step, each step takes a short time interval Δt. In solving the Schrödinger Eq. (3), within Δt, R can be fixed and Eq. (3) becomes
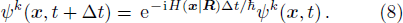
At the end of each step,
R moves Δ
R, which is determined by the Newtonian Eq. (
7).
For each step, during the interval Δt, the configuration is R, and ψ(x, t) is expanded in Eq. (4). At the end of that step, the time is t′ = t + Δt, the configuration becomes R′ = R + ΔR, and ψk(x, t + Δt) should be expanded by φn(x | R′),
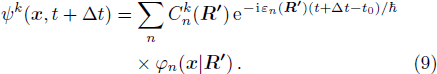
Substituting Eq. (
4) and Eq. (
9) into Eq. (
8),
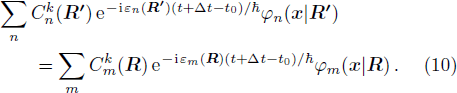
Making ⟨
φl(
x |
R′) | × Eq. (
10)
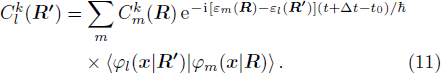
From Eq. (11), once the electronic state 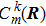 at t is known, the state
at t is known, the state 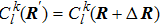 at t+Δt can be obtained.
at t+Δt can be obtained.
Thus, the evolution of the electronic state is demonstrated.
In each step, the starting time t can be taken as t0. Then Eq. (11) becomes
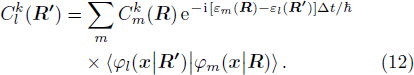
This equation shows that the evolution of the electronic state 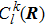 or ψk(x, t) contains two parts: The first part
or ψk(x, t) contains two parts: The first part 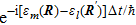 comes from Schrödinger equation, it is the dynamical evolution caused by the phase change. The second part ⟨φl(x | R′) |φn(x|R)⟩ comes from the transformation of base vector φl(x | R), it is the kinematic evolution.
comes from Schrödinger equation, it is the dynamical evolution caused by the phase change. The second part ⟨φl(x | R′) |φn(x|R)⟩ comes from the transformation of base vector φl(x | R), it is the kinematic evolution.
The rest problem is how to calculate the matrix ⟨φl(x|R + ΔR)|φn(x|R)⟩. A primary method is numerical calculation, and such method needs a lot of computer work. As usual, heavy numerical calculation may cause uncertainty, one is energy shift. If we can derive an analytic expression for the kinematic evolution ⟨φl(x|R′)|φm(x|R)⟩, it is desirable. This goal can be achieved by using the connection of fiber bundle. The details are presented in the following.
3 Connection of Fiber BundleThe change from configuration Ri to Rj is a deformation operator D(j, i), which includes unit element D(i, i)=I, inverse element D−1(i, j) = D(j, i), multiplication D(k, j) × D(j, i) = D(k, i), associativity of products [D(l, k) × D(k, j)] × D(j, i) = D(l, k) × [D(k, j) × D(j, i)]. Here, the multiplication has a restriction: two operators can multiply only they are connected. With such multiplication, the deformation operators form a special group, and the deformation group D(i, j) can be represented in terms of matrix, based on the Hamiltonian (1).
In base space R, at any point, a linear Hilbert space with the base vectors φn(x|R) can be attached, it is a fiber bundle.
During the deformation from R to R′, the bases are transformed from φn(x|R) to φn(x|R′). Since φn(x|R) are complete set, φn(x|R′) can be expanded in terms of φn(x|R),
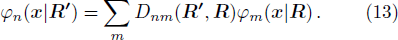
Here
Dnm(
R′,
R) is the transformation matrix between the base vectors
φn(
x|
R) and
φn(
x|
R′).
From Eq. (13), we can get
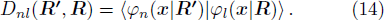
It is easy to see that the matrix
Dnl(
R′,
R) satisfies the multiplier rule, so
Dnl(
R′,
R) is a representation of the deformation group.
Very close to R(R1,R2,…,Rα,…,R3N), the coordinates of R′ are (R1,R2,…, Rα + Δ Rα,…,R3N). i.e. R′ = R + ΔRα,
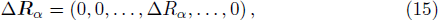
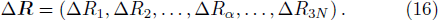
The change rate of the transformation matrix
Dnm(
R′,
R) in the component
Rα is
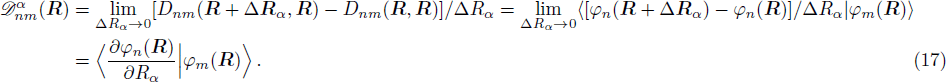
In geometry, this rate 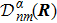 demonstrates the orientation correlation between neighboring base vectors of fiber bundles. Here, in the molecule, it is the connection of deformation. In base space R,
demonstrates the orientation correlation between neighboring base vectors of fiber bundles. Here, in the molecule, it is the connection of deformation. In base space R, 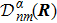 is a vector with the component index α. In the Hilbert space of fiber bundle,
is a vector with the component index α. In the Hilbert space of fiber bundle, 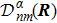 is a tensor with the indexes (n, m).
is a tensor with the indexes (n, m).
By the way, in algebra, 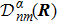 is the infinitesimal generator of the representation Dnl(R′, R).
is the infinitesimal generator of the representation Dnl(R′, R).
By using the perturbation theory, we can get
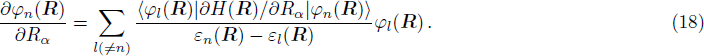
Substituting Eq. (
18) into Eq. (
17),
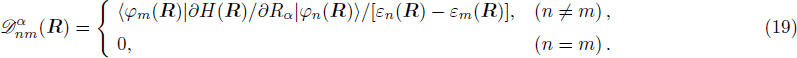
Since
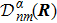
is a component in the direction
α,
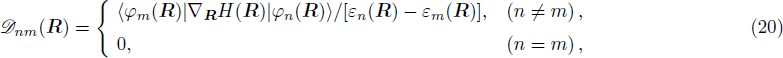
is the vector itself with 3
N components
, (
α = 1,2,...,3
N).
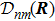
is the connection of molecule deformation. It is notable that the main part of the connection
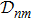
is the gradient matrix 〈
φm(
R)|∇
H(
R)|
φn(
R)〉, which has been got in Newtonian Eq. (
7).
By using 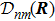 , from Eq. (17), we can get
, from Eq. (17), we can get
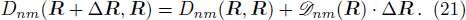
Therefore,
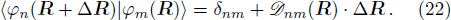
Substituting Eq. (
22) into Eq. (
12), we get
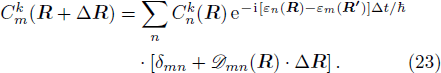
In Eq. (
23), the last term
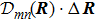
is the kinematic evolution, which has been analytically expressed by the connection
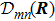
(Eq. (
20)) of the fiber bundle, and original heavy numerical calculation is avoided. If neglecting the connection the electronic state would not be able to spread over different eigenfunctions, that is the BOA.
Finally, by solving combined equations (7) and (23), the evolutions of electronic state ψ(x, t) and the nuclear configuration R(t) can be determined.
Polymers are chain-like molecules. Since they are one-dimensional systems, the polymers have prominent self-trapping, which is a typical deformation effect. The self-trapping produces many novel phenomena in polymers, such as photoinduced spin-flipping of charge carries and charge-flipping of spin carries. The Ehrenfest dynamics has been used to study these processes.[6–7] But these works have a problem, that their numerical calculations are very heavy, even getting some uncertainty. The connection of fibre bundle can be used to reduce the numerical calculation and make results transparent.
4 ConclusionMolecule is a physical model of the fiber bundle, which can be used to build analytic expression for molecular dynamics and simplify numerical calculation.