The chiral effective field theory (EFT) approach to few-nucleon systems^[1–2] has attracted much attention during the past two and a half decades. The problem of renormalization and power counting in this framework turned out to be highly nontrivial and caused controversial debates in the community. A number of formulations alternative to Weinberg’s original proposal have been suggested to resolve the issue of renormalization, see Refs. [3–8] for review articles. In our recent paper,^[9] we have compared a subtractive renormalization approach with the Wilsonian renormalization group (RG) approach^[10–11] in the context of the EFT for the two-nucleon system close to the unitary limit. In particular, within the subtractive scheme, we have identified the choices of renormalization conditions corresponding to the Kaplan-Savage-Wise (KSW),^[12] see also Refs. [13–14], and Weinberg^[1] power counting schemes. The standard Wilsonian RG method with a single cutoff scale is, on the other hand, only compatible with the KSW counting scheme. We argued that this mismatch is caused by the too restrictive formulation of the Wilsonian RG approach in its conventional form, which does not take into account the full freedom in the choice of renormalization conditions in EFT. This is the origin of the often made (incorrect, see Ref. [9]) statement that the Weinberg power counting scheme for two-nucleon scattering corresponds to the expansion around a trivial fixed point.

In the Wilsonian RG approach one integrates out degrees of freedom with energies higher than some cutoff scale and systematically exploits the cutoff-parameter dependence of coupling constants to ensure that physics at energies below the cutoff scale remains unchanged.^[15] In contrast, the Gell-Mann-Low RG equations determine the dependence of various quantities on the scale(s) of renormalization.^[16] In renormalizable (in the traditional sense) theories only logarithmic divergences contribute to the renormalization of the coupling constants and, therefore, there is a direct correspondence between the two approaches. On the other hand, in EFTs with non-renormalizable interactions, power-law divergences have to be taken care of and the direct link between the two RG equations is lost. Notice further that in theories with more than one coupling constant, as it is the case in EFTs, each coupling is attributed its own renormalization scale. In the Wilsonian approach one usually introduces a single cutoff scale and studies how various parameters of a theory depend on it. However, in certain cases such as e.g. the few-nucleon problem in chiral EFT, it is advantageous to exploit the freedom of choosing several renormalization scales independently.^[9,17]

In this paper we fill this gap and generalize the Wilsonian RG analysis of low-energy two-particle scattering in the framework of the Lippmann-Schwinger (LS) equation, pioneered in Ref. [10], by introducing a multitude of cutoff parameters. We obtain a system of integro-differential RG equations describing the dependence of the potential on several cutoff scales. As an application, we study a perturbative solution of the obtained system of equations for the case of two cutoff parameters by making an ansatz for the potential in the form of a Taylor series expansion in powers of momenta. We demonstrate that the resulting potential indeed obeys the Weinberg power counting for the choice of renormalization conditions suggested in Ref. [9].

Our paper is organized as follows. In the next section we derive the system of RG equations for the case of several cutoff parameters. In Sec. 3, we present the perturbative solution of this system of equations and discuss the obtained results in the context of EFT for two-nucleon scattering. Finally, our main findings are briefly summarized in Sec. 4.

To introduce a multitude of cutoff parameters and derive the corresponding system of RG equations we start with the fully off-shell LS equation

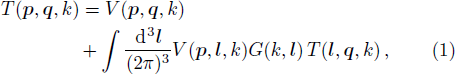
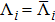
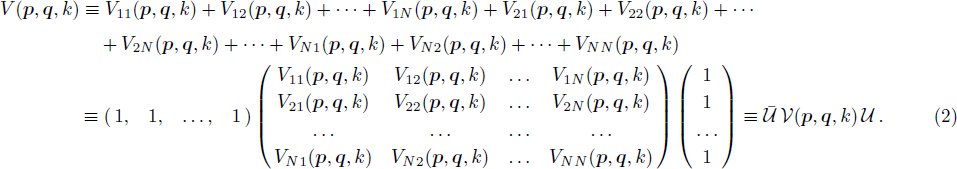
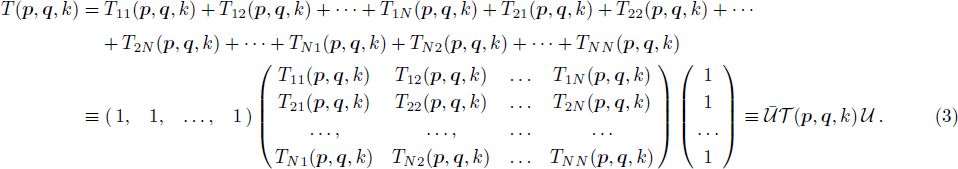
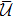
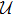
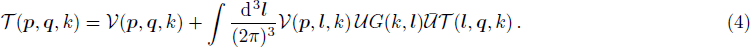
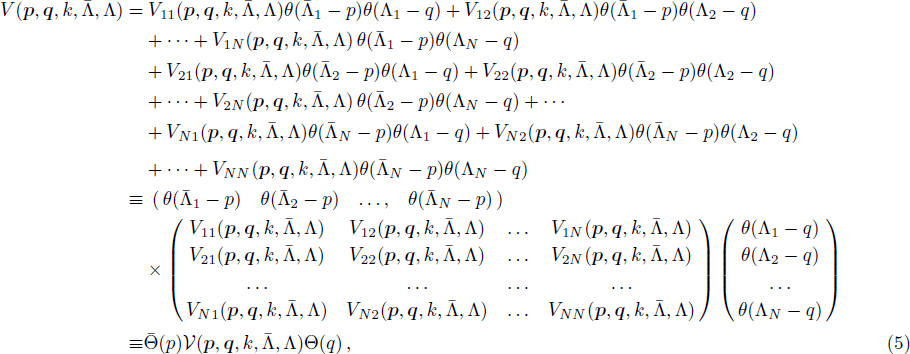
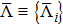
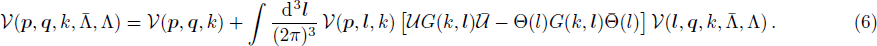
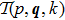
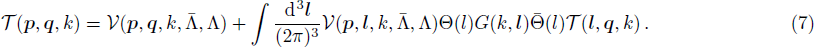
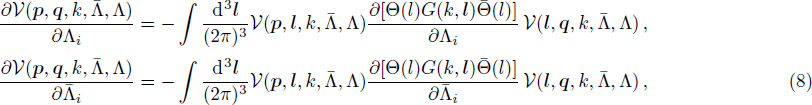
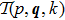
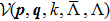
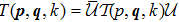
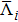
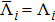
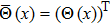
The case of Hermitean cutoff-dependent potentials corresponds to choosing for all i, so that . Furthermore, for a single cutoff parameter, Eq. (8) reduces to the differential RG equation of Ref. [10]. In general, Eq. (8) is a system of integro-differential equations, however in some cases such as e.g. for separable potentials, it can be reduced to a system of differential equations.

In exact analogy to the previous section, one can obtain a system of RG equations for the LS equation in partial wave basis

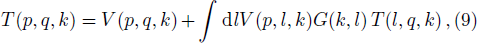
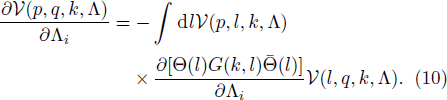
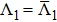
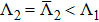
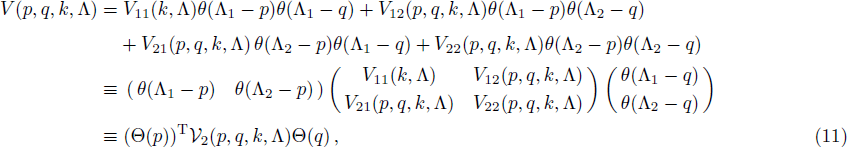
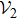
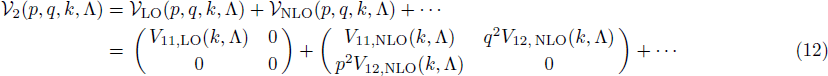
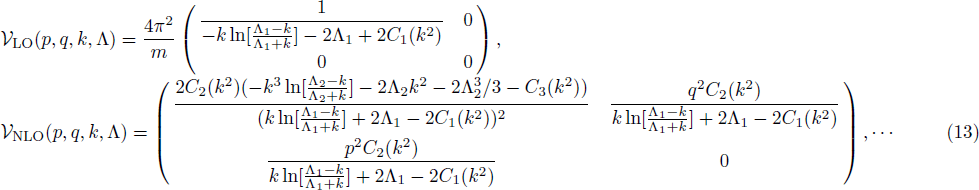
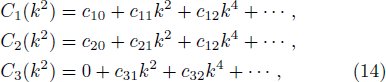
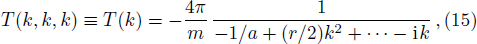
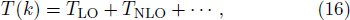
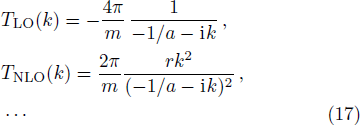
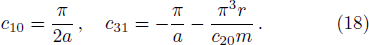
As a simple application, we solve the RG equations with two cutoff parameters, and , as a perturbative power series expansion in the small parameters, p, q, k, and Λ₂. Specifically, we consider the cutoff regularized potential of the form

Substituting the obtained values of c_ij back into the potential, we find

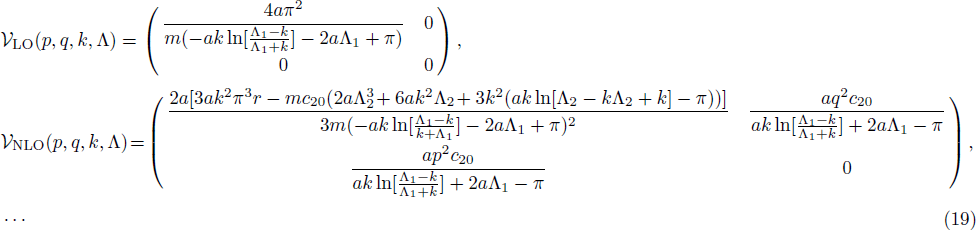
Our paper provides a generalization of the Wilsonian renormalization group approach to the Lippmann-Schwinger equation for two-particle scattering at low energy by introducing a multitude of cutoff parameters. We derive a system of integro-differential equations for the cutoff regularized potential, which reduces to the RG equation of Ref. [10] for the case of a single cutoff. As a simple application, we considered a perturbative solution of the system of RG equations in the form of a power series expansion in momenta and energy. We have demonstrated that by introducing two cutoff parameters, one obtains a perturbative expansion of the potential which follows the Weinberg power counting rules,^[2] while as shown in Ref. [10], the usage of a single cutoff parameter leads to the power counting of Refs. [12–14]. This simple example demonstrates that the enlargement of the space of the renormalization group parameters by exploiting the full freedom in the choice of renormalization conditions can be advantageously used in the context of the low-energy EFT for nucleon-nucleon scattering. It will be interesting to apply the presented formalism with the multitude of cutoff parameters to the case of the potentials with a long-range interaction. This work is in progress.