Cite this Article
Shi Hong-Jun, Miao Lian-Ying, Sun Yong-Zheng, Liu Mao-Xing. Fixed-Time Outer Synchronization of Complex Networks with Noise Coupling. Communications in Theoretical Physics, 2018, 69(3): 271  
Permissions
Fixed-Time Outer Synchronization of Complex Networks with Noise Coupling
Shi Hong-Jun1, Miao Lian-Ying1, Sun Yong-Zheng1, †, Liu Mao-Xing2
School of Mathematics, China University of Mining and Technology, Xuzhou 221008, China
School of Science, North University of China, Taiyuan 030051, China

 

† Corresponding author. E-mail: yzsung79@outlook.com

Abstract
Abstract

In this paper, the fixed-time outer synchronization of complex networks with noise coupling is investigated. Based on the theory of fixed-time stability and matrix inequalities, sufficient conditions for fixed-time outer synchronization are established and the estimation of the upper bound of the setting time is obtained. The result shows that the setting time can be adjusted to a desired value regardless of the initial states. Numerical simulations are performed to verify the effectiveness of the theoretical results. The effects of control parameters and the density of controlled nodes on the converging time are studied.

PACS: ;05.45.Xt;;05.45.-a;
Keyword:outer synchronization;fixed-time;complex network;noise coupling
1 Introduction

Since being proposed by Pecora and Carroll,[1] synchronization in coupled systems has been extensively studied in many areas, such as biological systems, information processing, economical systems, etc.[2–11] Many kinds of synchronization have been explored, involving complete synchronization,[12] generalized synchronization,[13–14] projective synchronization,[15] and lag synchronization.[16] Due to its widely applications, different control techniques have been constructed, such as adaptive control,[17–19] pinning control,[20] finite-time control,[21–24] sliding mode control,[23,25] and so on.

As a hot research topic, the outer synchronization of complex networks has been extensively investigated.[14,19,26–27] Different from the inner synchronization happening inside a network, outer synchronization is referred as synchronization occurring between two or more networks. In Refs. [14, 27], based on the LaSalle-type invariance principle for stochastic differential equations, the outer synchronization between two nonidentical networks with noise coupling was investigated. The adaptive outer synchronization between two complex delayed networks was discussed in Ref. [19]. Sufficient criterion for outer synchronization between two coupled discrete-time networks were established in Ref. [26].

Most previous works on network synchronization can be divided into two classes: infinite-time synchronization and finite-time synchronization. Finite-time synchronization means that the trajectories of the response system can reach to those of the drive system in a finite horizon, which is very important and significant in the practical engineering process. Because of the fact that the finite settling time is heavily dependent on the initial conditions of the system, it is necessary to obtain the initial states in advance. Nevertheless, the knowledge of initial conditions may be hard to achieve or even impossible to estimate in practical applications. To overcome this obstacle, a new approach named fixed-time control has been proposed.[20,28–34]

Fixed-time control implies that the system is globally finite-time stable and the convergence settling time is bounded and independent of the initial states. Thus, this new technique has important practical implications. For example, to ensure excellent power supply quality and avoid voltage collapse, we should eliminate the frequency deviation and stabilize the voltage of power systems to its nominal value within a limited time. In Ref. [29], for chaos suppression and voltage stabilization in some three-bus power systems, a fixed-time sliding mode control approach was proposed. To realize the finite-time and fixed-time cluster synchronization, Liu and Chen designed simple distributed protocols with or without pinning control.[30] For a class of delayed memristor-based recurrent neural networks, Cao and Li established sufficient conditions of fixed-time synchronization.[31] Hong et al. found that fixed-time control protocols can guarantee any prescribed convergence time regardless of the initial states.[32] In Ref. [33], for fixed-time stabilization of single-input and multi-input systems, Polyakov proposed two different types of nonlinear controller. Based on the Lyapunov methods, a fixed-time terminal sliding-mode control technique for the second-order nonlinear systems was investigated in Ref. [34]. To our best knowledge, there are few results on the fixed-time outer synchronization of complex networks with noise coupling. Actually, noise may play an important role on the collective dynamics of complex systems,[35] which inspired us to study the effect of noise on the fixed-time outer synchronization.

In this paper, based on the theory of fixed-time stability and matrix inequalities, sufficient conditions for the fixed-time outer synchronization of complex networks with noise coupling are presented. The theoretical results show that the setting time can be adjusted to a desired value regardless of the initial states. To verify the effectiveness of the proposed synchronization scheme, numerical simulations are performed.

The rest of this paper is organized as follows. In Sec. 2, the network modeling and some preliminaries are given. In Sec. 3, sufficient conditions for fixed-time outer synchronization are established. In Sec. 4, numerical simulations are given to verify the effectiveness of the proposed control schemes. Section 5 concludes this paper.

2 Network Modeling and Preliminaries

Consider a complex network consisting of N nodes with linear couplings:

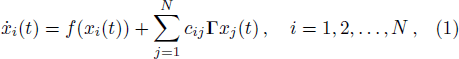
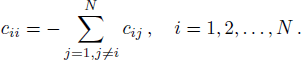
where xi(t) = (xi1, . . ., xin)T ∈ Rn is the state vector of the i-th node, f: Rn → Rn is a continuously differentiable nonlinear vector function, Γ is the inner coupling matrix, C = (cij)N×N represents the coupling configurations of the network, whose entries cij are defined as follows: if there is a link from node j to node i (i ≠ j) then set cij > 0, otherwise cij = 0 (i ≠ j). The diagonal elements of matrix C are defined as

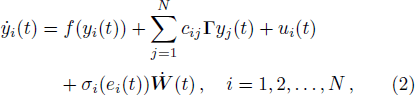
In order to achieve the fixed-time outer synchronization between complex networks with noise coupling, we refer to model (1) as the drive network, and the response network is given by the following equations:

where yi(t) = (yi1, . . ., yin)T ∈ Rn is the state vector of node i, ei(t) = yi(t) − xi(t) (i = 1, 2, . . ., N) are the synchronization errors between networks (1) and (2), ui(t) (i = 1, 2, . . ., N) are the controllers to be designed. The noise term in system (2) is often used to describe the coupling process influenced by many factors, such as inaccurate design of coupling strength and environmental fluctuation. Here σi : Rn → Rn × s is the noisy intensity matrix, W = (w1, . . ., ws)T is an s-dimensional Brownian motion defined on a complete probability space with a natural filtration .

In order to get our main results in the next section, we state here some needed concepts, assumptions and lemmas.

To achieve the complete outer synchronization in fixed time, we design

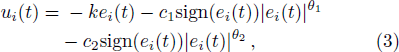
where sign(ei(t)) = diag(sign(ei1(t)), . . ., sign(ein(t))), |ei(t)|θ = (|ei1(t)|θ, . . .,|ein(t)|θ)T, k, c1, and c2 are positive constants, and control parameters satisfy 0 < θ1 < 1, θ2 > 1.

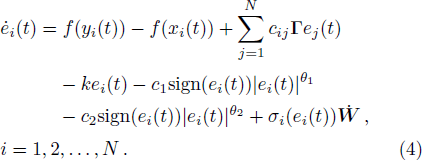
From Eqs. (1) and (2), we have the following error system:

In fact, if we consider the outer synchronization between two different networks, both the topological structure and the node dynamics may be different. The response network can be restructured as follows:

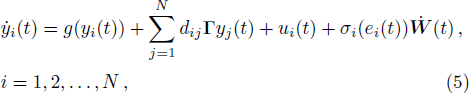
where g : Rn → Rn is continuously differentiable, D = (dij)N×N is the coupling configuration matrix, which is similar to the definition of matrix C, ei(t) = yi(t) − ϕ(xi(t)) is the generalized synchronization error between networks (1) and (5), ϕ : Rn → Rn is a given continuously differentiable map and ϕ(xi) = (ϕ1(xi), ϕ2(xi), . . ., ϕn(xi))T. The controllers ui(t) in Eq. (5) are to be designed.

Since the speed of the environmental fluctuations is much less than the change rate of concrete systems,[18,27,36–38] for the noise intensity function, we have the following assumption:

Moreover, σ(0) ≡ 0.

For the n-dimensional stochastic differential equation:[39]

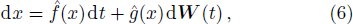
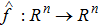
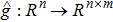
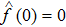
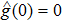
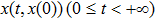
where x ∈ Rn is the state vector, and and are continuous and satisfy , . It is supposed that Eq. (6) has a unique and global solution denoted by , where x(0) is the initial state of Eq. (6).

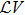
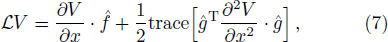
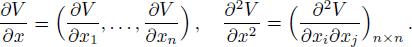
For each V ∈ C2,1(Rn × R+, R+), the operator associated to Eq. (6) is defined as:

where

3 Main Results
3.1 Fixed-Time Complete Outer Synchronization

Using matrix transpose properties, one has

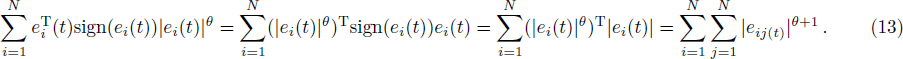
By Lemma 3 and 0 < θ1 < 1, θ2 > 1, we have

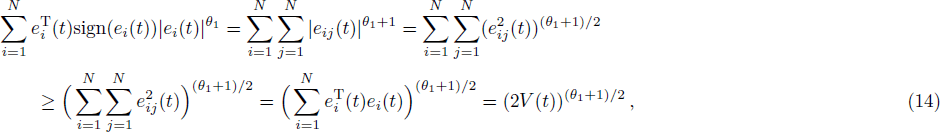
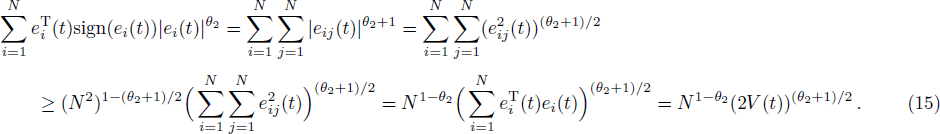
Thus

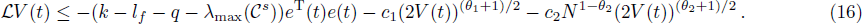
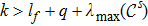
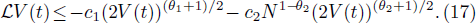
If then we have

From the Itô formula, we have

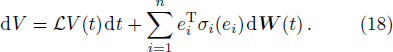
Taking the expectations on both sides of Eq. (18), we obtain

Let α = c1 2(θ1+1)/2, β = c2N1−θ2 2(θ2+1)/2, and p = (θ1 + 1)/2, q = (θ2 + 1)/2, then

From Lemma 1, we can get the conclusion and the fixed settling time T0 can be estimated as Eq. (8). This completes the proof of Theorem 1.

3.2 Fixed-Time Generalized Outer Synchronization

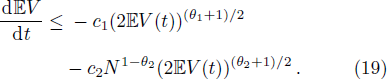
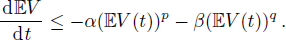
The fixed-time complete outer synchronization can not be achieved if two networks have different dynamics. In the following, we consider the generalized outer synchronization between networks (1) and (5). For the given continuously differentiable map ϕ(·), the dynamic behavior of generalized synchronization error ei(t) = yi(t) − ϕ(xi(t)) between networks (1) and (5) can be described as follows:

where Dϕ(xi(t)) is the Jacobian matrix of the map ϕ(xi(t)):

The controllers ui(t) are designed as follows:

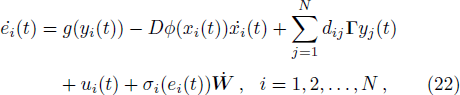
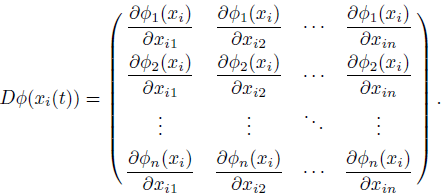
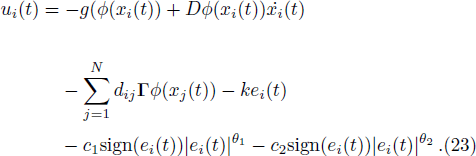
By Eq. (7), one has

From Assumption 1, we obtain

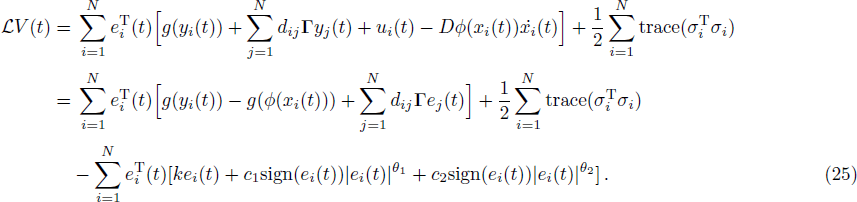
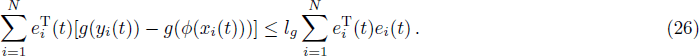
Note that

we can further obtain

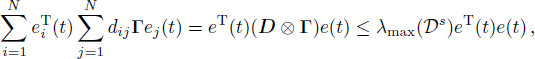
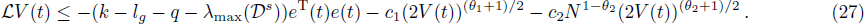
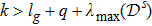
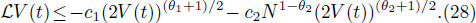
If , we have

The rest is similar to the proof of Theorem 1 and is therefore omitted.

4 Numerical Simulations

In this section several numerical results are given to verify the effectiveness of the theoretical results. In the simulations, the Euler-Maruyama numerical scheme[42] for stochastic differential equations was used. Without loss of generality, we take the inner coupling matrix Γ as an identity matrix. The initial conditions of the nodes are randomly taken from the interval [−1, 1]. The total synchronization error E(t) = ‖e(t)‖ is used to measure the evolution process and the convergence indicator T0 is defined as: T0 = inf{t1 : E(t) < 10−4, ∀t ≥ t1}.

4.1 Numerical Example of Complete Synchronization

We take the Rössler-like system as the node dynamics of networks (1) and (2), which can be described as

where x = (x1, x2, x3)T ∈ R3 is the state vector,

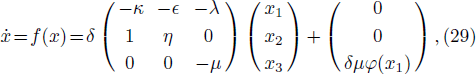
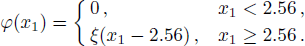
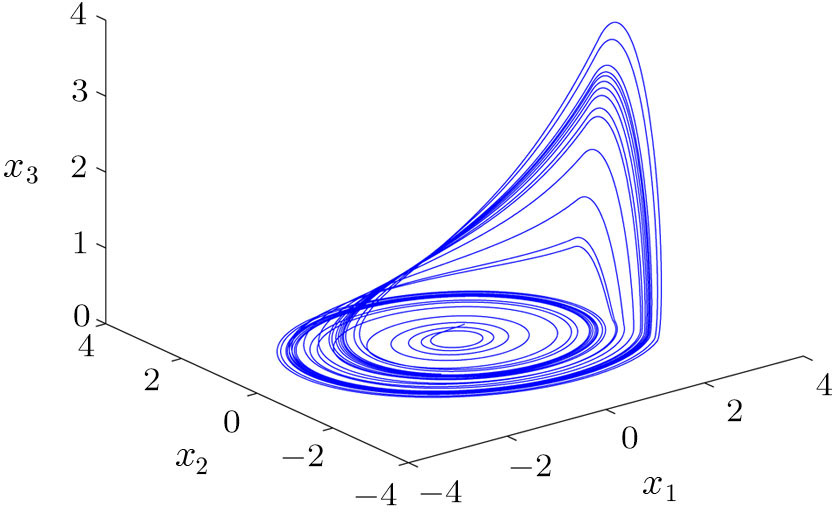As shown in Fig. 1, the Rössler-like system has a chaotic attractor when δ = 0.03, ϵ = 1.5, η = 0.2, μ = 1.5, λ = 0.75, ξ = 21.43, and κ = 0.075. It is easy to verify that the continuously differentiable nonlinear vector function f : Rn → Rn satisfied the Assumption 1 with lf = 0.4926.

Fig. 1 Chaotic attractor generated by the system (29) when δ = 0.03, ϵ = 1.5, η = 0.2, μ = 1.5, λ = 0.75, ξ = 21.43, and κ = 0.075.

Let , . Then, σi(ei(t)) satisfies the locally Lipschitz condition and the linear growth condition, i.e., . To verify the effectiveness of the proposed synchronization scheme in Theorem 1, we take C = (cij)N×N as the coupling configurations of BA scale-free network[43] with m0 = 10, m1 = 5, where m0 is the number of starting vertices and m1 is the degree of new vertex added at each time step.

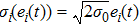
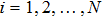
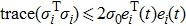
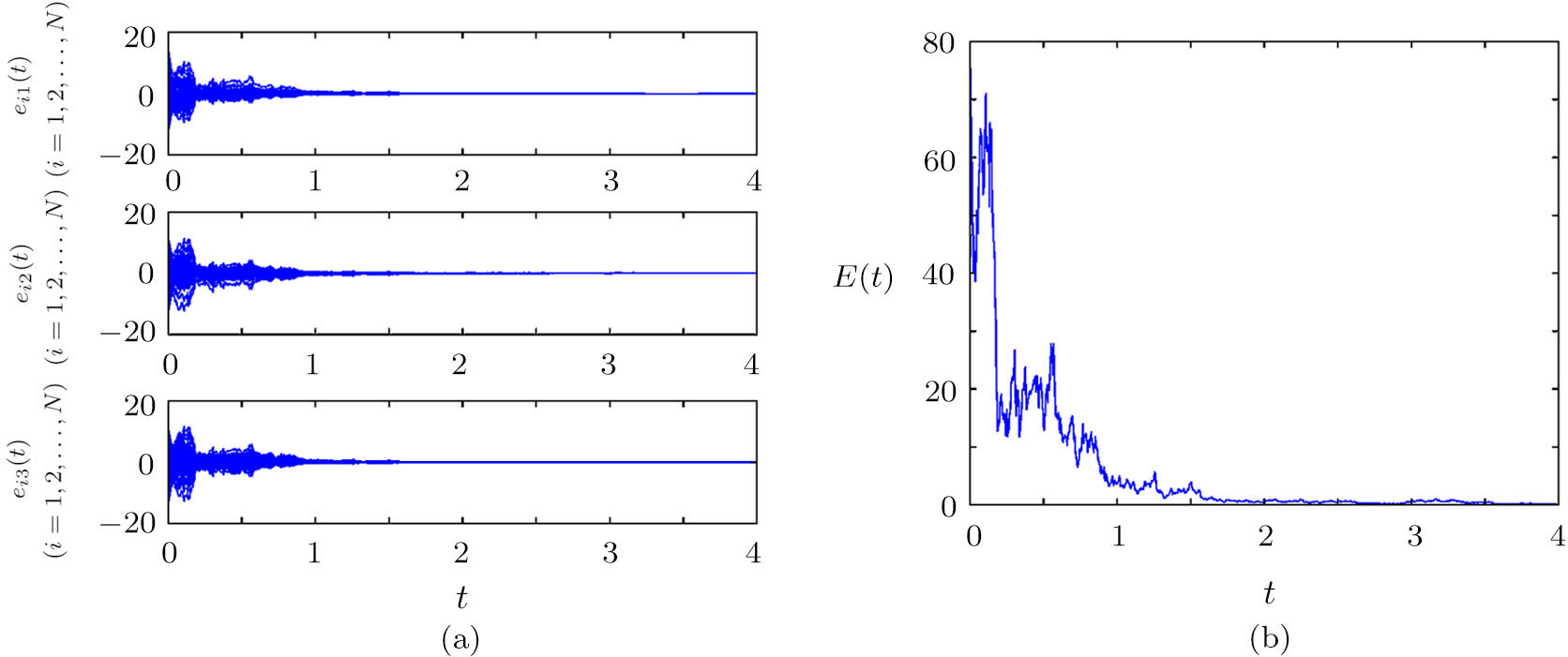
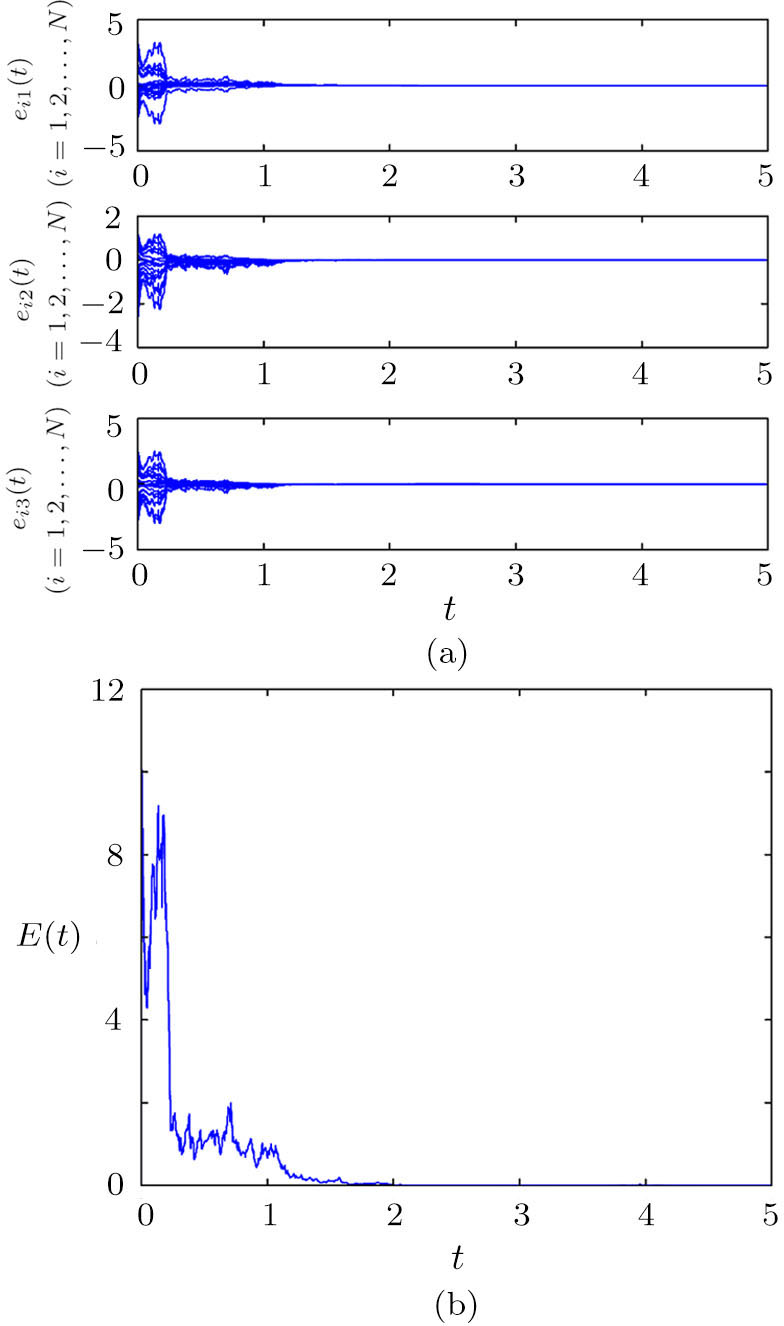For brevity, taking N = 100 and σ0 = 1.9, we simulate the evolution of the networks according to the controllers defined in Eq. (3) with the parameters k = 0.6, c1 = 0.1, c2 = 0.2, θ1 = 0.5, θ2 = 1.5. Figure 2 shows the trajectories of synchronization error eij(t) (i = 1,2, . . ., 100; j = 1, 2, 3) and the total synchronization error E(t). From Fig. 2, one can find that the fixed-time outer synchronization is realized, and the simulation matches the theoretical results perfectly.

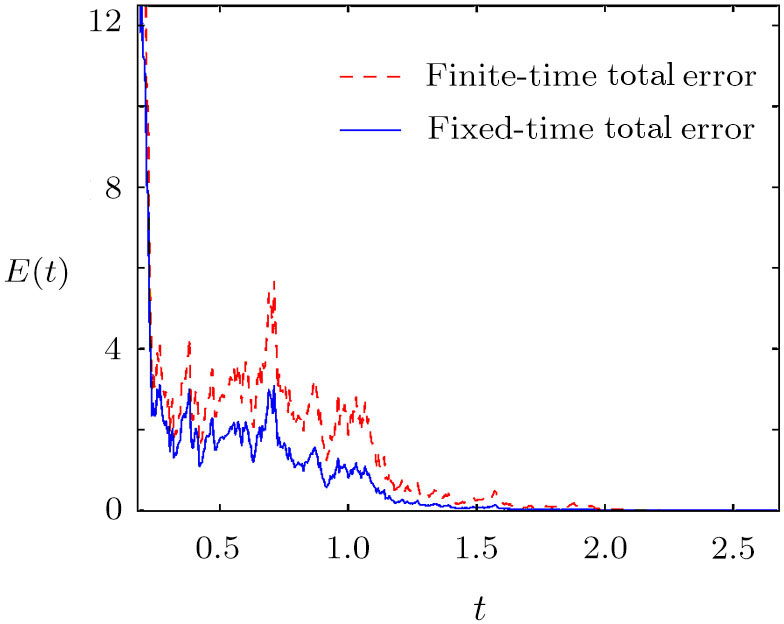
Fig. 2 Trajectories of the synchronization error (a) and the total synchronization error (b) between networks (1) and (2) with N = 100, σ0 = 1.9 and k = 0.6, c1 = 0.1, c2 = 0.2, θ1 = 0.5, θ2 = 1.5.

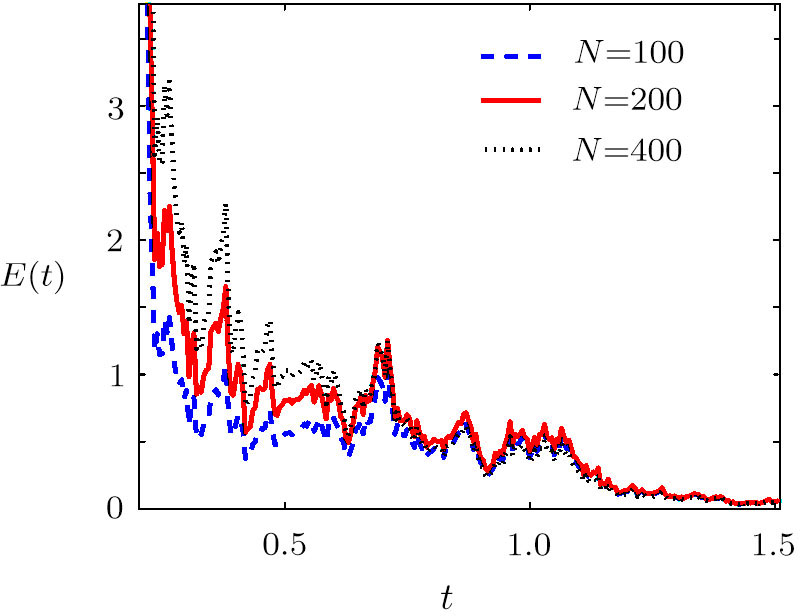Compared with finite-time synchronization, the settling time of fixed-time synchronization is bounded and independent of the initial states. Figure 3 gives the trajectories of the total synchronization error E(t) with fixed-time control (c2 = 0.2) and finite-time control (c2 = 0). It is shown that the convergence rate of fixed-time synchronization is faster than that of finite-time synchronization. Compared to finite-time control, fixed-time control strategy shows more superiority. From inequality (21), we can see that the upper bound of the convergence time is determined by the network size N. Figure 4 shows that the more nodes of networks, the slower the convergence rate of complex networks is.

Fig. 3 Trajectories of the total synchronization error between networks (1) and (2) with finite-time control (c2 = 0) and fixed-time control (c2 = 0.2), the parameters N = 100, σ0 = 1.9 and k = 0.6, θ1 = 0.5, θ2 = 1.5.
Fig. 4 Trajectories of the total synchronization error between networks (1) and (2) when σ0 = 1.9, k = 0.6, c1 = 0.1, c2 = 0.2, θ1 = 0.5, θ2 = 1.5, and N = 100, 200, 400.

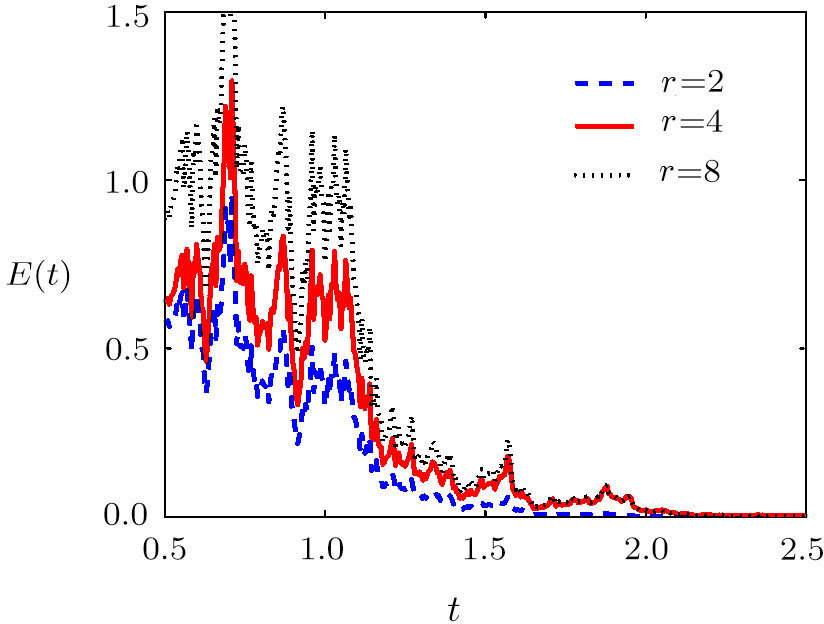To obtain a more accurate estimation of T0, we can appropriately adjust the parameter γ of the controller (20). Figure 5 indicates that the convergence speed decreases with the increasing of the parameter γ.

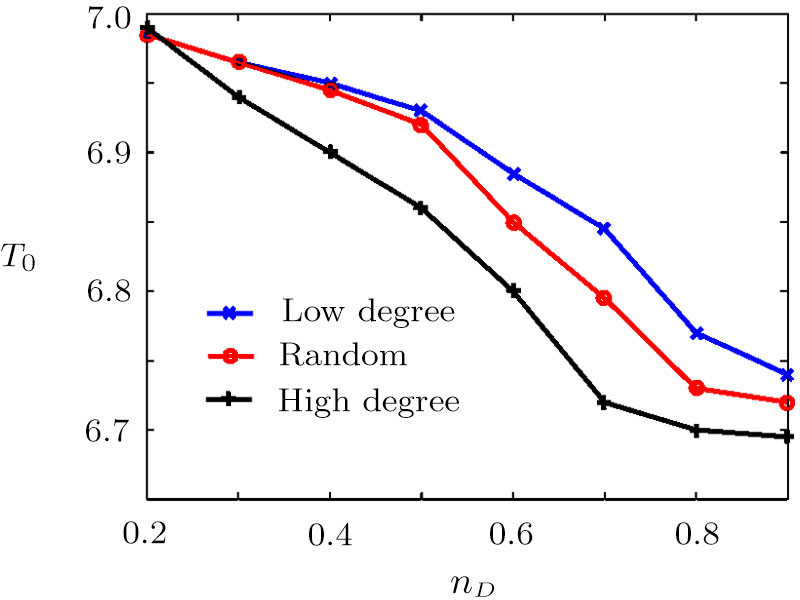
Fig. 5 Trajectories of the total synchronization error between networks (1) and (2) when σ0 = 1.9, k = 0.6, c1 = 0.1, c2 = 0.2 and γ = 2, 4, 8.

Actually, the fixed-time synchronization of complex networks may be achieved without controlling all the network nodes. In fact, many complex networks contain large number of nodes, taking all nodes under control is high-cost and difficult to implement. Therefore, pinning control scheme,[16,20,30,44] which only needs a small fraction of nodes to be controlled, is more suitable to control complex networks to reduce computational burden and equipment resource. The effects of choosing different pinning schemes (high-degree, low-degree and random) on the convergence speed are exhibited in Fig. 6, where nD is the percentage of controlled nodes in all nodes. It is shown that the high-degree control can minimize the convergence time T0, followed by random control, the worst is low-degree control.

Fig. 6 The effect of different pinning schemes on the convergence indicator of Scale-free networks with N = 400, σ0 = 1.9, k = 0.6, c1 = 0.1, c2 = 0.2, θ1 = 0.5, θ2 = 1.5.
4.2 Numerical Example of Generalized Synchronization

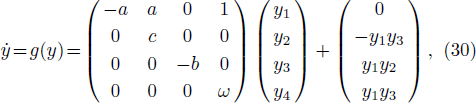
To demonstrate the effectiveness of Theorem 2, we take the Rössler-like system (29) and hyperchaotic Lü system as the node dynamics of networks (1) and (5), respectively. The hyperchaotic Lü system can be described as

where a = 36, b = 3, c = 20, ω = 0.4.

Let the continuously differentiable map ϕ : R3 → R4 be

Then

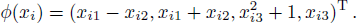
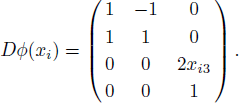
For brevity, taking N = 100 and σ0 = 1.9, we also take D = (dij)N×N as a new coupling configurations of BA scale-free network with m0 = 10, m1 = 6, and simulate the evolution of the networks according to the controllers defined in Eq. (23) with the parameters k = 0.6, c1 = 0.1, c2 = 0.2, θ1 = 0.8, θ2 = 1.3. From Fig. 7, one can find that the fixed-time generalized outer synchronization is realized, which confirms the theoretical analysis of Theorem 2.

Fig. 7 Trajectories of the fixed-time generalized synchronization error (a) and the total generalized synchronization error (b) between networks (1) and (5) with N = 100, σ0 = 1.9 and k = 0.6, c1 = 0.1, c2 = 0.2, θ1 = 0.8, θ2 = 1.3.
5 Conclusion

In this paper, we have investigated the fixed-time outer synchronization between complex networks with noise coupling. Based on the fixed-time control method and inequality techniques, sufficient conditions of fixed-time outer synchronization are proposed. The theoretical analysis indicates that the upper bound of convergence time is determined by the network size N. To verify the effectiveness of the proposed synchronization scheme, for a given scale-free network, numerical simulations are performed and the effects of different pinning schemes on the convergence rate are analyzed. Compared with finite-time synchronization, the settling time of fixed-time synchronization is bounded and independent of the initial states, and thus, has a better performance. Note that time delay may influence the dynamic behavior of complex networks, the fixed-time outer synchronization of time-delayed complex networks is our future direction.

Reference
[1] Barabási A. L. Albert R. Science 286 1999 509
[2] Watts D. J. Strogatz S. H. Nature (London) 393 1998 440
[3] Pecora L. M. Carroll T. L. Phys. Rev. Lett. 80 1998 2109
[4] Barabási A. L. Science 325 2009 412
[5] Yu W. Cao J. Lü J. SIAM J. Appl. Dyn. Syst. 7 2008 108
[6] Lü J. Yu X. Chen G. Physica A 334 2004 281
[7] Klovdahl A.S. Soc. Sci. Med. 21 1985 1203
[8] Sun Y. Leng S. Lai Y. et al. Phys. Rev. Lett. 119 2017 198301
[9] Begon M. Townsend C. Harper J. Ecology: Individuals, Populations and Communities Blackwell Sci. London 1996
[10] Wang J. Zhang J. Yuan Z. et al. J. Biol. Rhythms 23 2008 472
[11] Nishikawa T. Motter A. E. Lai Y. Hoppensteadt F. C. Phys. Rev. Lett. 91 2003 014101
[12] Landsman A. S. Schwartz I. B. Phys. Rev. E 75 2007 026201
[13] Wu Y. Li C. Wu Y. Kurths J. Commun. Nonlinear Sci. Numer. Simul. 17 2012 349
[14] Sun Y. Li W. Ruan J. Commun. Nonlinear Sci. Numer. Simul. 18 2013 989
[15] Yao H. Wang S. Chin. Phys. B 21 2012 110506
[16] Sun W. Wang S. Wang G. Wu Y. Nonlinear Dyn. 79 2015 2659
[17] Tang H. Chen L. Lu J. Tse C.K. Physica A 387 2008 5623
[18] Wang W. Li L. Peng H. Yang Y. Nonlinear Dyn. 76 2014 591
[19] Wu X. Lu H. Neurocomputing 82 2012 157
[20] Liu X. Chen Z. Zhou L. J. Frankl. Inst-Eng. Appl. Math. 354 2017 15
[21] Sun Y. Li W. Zhao D. Chaos 22 2012 023152
[22] Yang X. Cao J. Appl. Math. Model 34 2010 3631
[23] Sun J. Wang Y. Wang Y. Shen Y. Nonlinear Dyn. 85 2016 1105
[24] Sun Y. Li W. Ruan J. Commun. Theor. Phys. 58 2012 697
[25] Liu S. Chen L. Chin. Phys. B 22 2013 100506
[26] Li C. Xu C. Sun W. Kurths J. Chaos 19 2009 013106
[27] Wang G. Cao J. Lu J. Physica A 389 2010 1480
[28] Li R. Cao J. Alsaedi A. Alsaadi F. Appl. Math. Comput. 313 2017 37
[29] Ni J.K. Liu L. Liu C. et al. Nonlinear Dyn. 86 2016 401
[30] Liu X. Chen T. IEEE T. Cybern. 99 2016 1
[31] Cao J. Li R. Sci. China-Inf. Sci. 60 2017 032201
[32] Hong H. Yu W. Wen G. Yu X. IEEE Trans. Syst. Man Cybern. 47 2017 1464
[33] Polyakov A. IEEE Trans. Autom. Control. 57 2012 2106
[34] Zuo Z. IET Contr. Theory Appl. 9 2015 545
[35] Sun Y. Lin W. Chaos 25 2015 083118
[36] Cai S. Zhou P. Liu Z. Nonlinear Dyn. 76 2014 1677
[37] Sun Y. Ruan J. Chaos 19 2009 043113
[38] Wang J. Feng J. Xu C. Zhao Y. Commun. Nonlinear Sci. 18 2013 3146
[39] Mao X. Stochastic Differential Equations and Applications Horwood, England 1997
[40] Lu W. Liu X. Chen T. Neural Networks 81 2016 11
[41] Khalil H. K. Grizzle J. W. Nonlinear Systems Prentice Hall New Jersey 2002
[42] Kloeden P.E. Platen E. Numerical Solution of Stochastic Differential Equations Springer Heidelberg 1992
[43] Wang X. Chen G. IEEE Trans. Circuits Syst. I-Fundam 49 2002 54
[44] Yu W. Chen G. Lü J. Automatica 45 2009 429