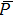† Corresponding author. E-mail:
Recently, the notion of non-standard Lagrangians was discussed widely in literature in an attempt to explore the inverse variational problem of nonlinear differential equations. Different forms of non-standard Lagrangians were introduced in literature and have revealed nice mathematical and physical properties. One interesting form related to the inverse variational problem is the logarithmic Lagrangian, which has a number of motivating features related to the Liénard-type and Emden nonlinear differential equations. Such types of Lagrangians lead to nonlinear dynamics based on non-standard Hamiltonians. In this communication, we show that some new dynamical properties are obtained in stellar dynamics if standard Lagrangians are replaced by Logarithmic Lagrangians and their corresponding non-standard Hamiltonians. One interesting consequence concerns the emergence of an extra pressure term, which is related to the gravitational field suggesting that gravitation may act as a pressure in a strong gravitational field. The case of the stellar halo of the Milky Way is considered.
Recently, the notion of non-standard Lagrangians (NSL) was extensively explored in literature in an attempt to explore the inverse variational problem of some familiar nonlinear differential equations.[1] A number of motivating results were obtained in the theory of dissipative dynamical systems,[2–6] geometric and nonlinear dynamics,[7–18] plasma physics,[19] quantum theory,[20–22] relativity,[23–25] and electromagnetic theory.[26] Despite the wide range of applications of NSL, the topic still requires more attention and deserves more concentration and studies. It is noteworthy that NSL are more appreciated by mathematicians than physicists and we already know the main reason. In physics, the meaning of NSL is still unclear, no physical foundation was studied carefully and accordingly they serve mathematicians more than physicists. This is an open dilemma that deserves a serious analysis. In applied mathematics and mainly in the framework of dynamical systems, NSL may increase the number of the initial data required to fix the classical trajectory and generate dynamical equations that go beyond the standard Newton’s law paradigm. NSL came in a large number of mathematical forms.[6] One interesting form introduced in literature is the Logarithmic Lagrangian (LL),[27] which possesses some interesting properties related to the Liénard-type and Emden nonlinear differential equations. In fact, such forms of Lagrangians were introduced in order to study the root of reciprocal Lagrangians in the theory of inverse variational problem. Motivated by LL, the main aim of this paper is to introduce the corresponding non-standard Hamiltonians and to discuss some of its implications in stellar dynamics. We have selected this topic due to its double impacts in applied mathematics and physics. In reality, the stellar dynamics and the motion of stars within galaxies are getting more and more recognized to be important both in applied mathematics and practical applications as they connect the microscopic and macroscopic kinetic theory of gases and fluids. In fact, the collisionless Boltzmann equation, which is the subject of this paper, is the most classical but fundamental equation in the kinetic theory used to describe the motion of stars within galaxies, which allows the numbers of stars to be calculated as a function of position and velocity in the galaxy. However, it is well-known that the collisionless Boltzmann equation can be derived using Hamiltonian’s equations. As the LL approach is expected to modify the Hamilton’s equations of motion, we expect accordingly that the Boltzmann equation is modified as well. We are curious to know the implications of the modified Boltzmann equation in stellar dynamics. The paper is organized as follows: in Sec.
We start by introducing the basic setups of the LL approach.
Let time 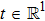
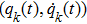
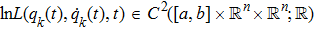
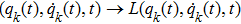
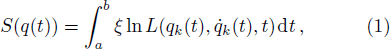
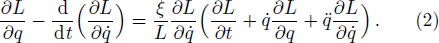
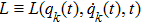
In what follows, we suppose for simplicity that the Lagrangian does not depend on time. The action principle can also be carried out on the phase space in the Hamiltonian formalism. We introduce a family of conjugate momenta from the family of Lagrangian 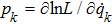
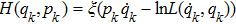
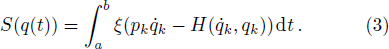
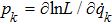
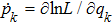
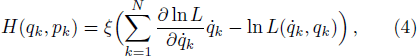
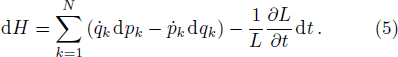
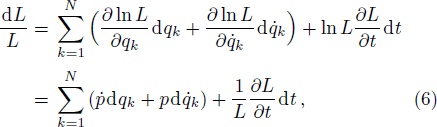
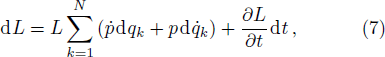


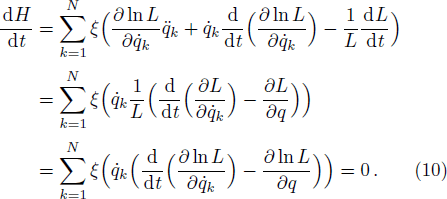
Equations (
In the framework of the semiclassical transport theory, the Boltzmann equation governs the spatio-temporal evolution of the particle gas. In fact, galaxies are collisionless systems as their relaxation time is very long. Hence, the motion of stars within galaxies can be described by the collisionless Boltzmann equation. This equation can be derived using Hamiltonian mechanics. In this section, the MCBE will be derived from the modified Hamiltonian equations (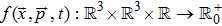
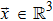
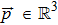
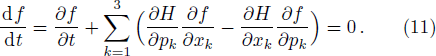
For the case of a star of mass m moving in a gravitational field Φ, the Hamiltonian is 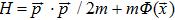
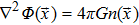
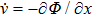
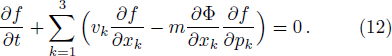
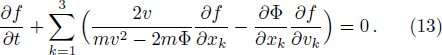
In fact, the first three integrals are standard and their derivations are found in many hydrodynamics books, e.g. Refs. [38–39]. The last integral gives:
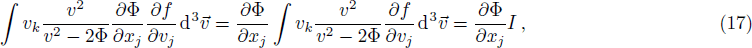
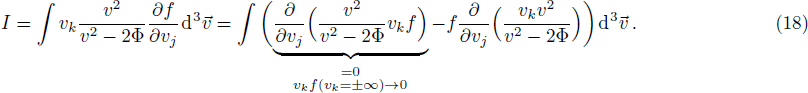
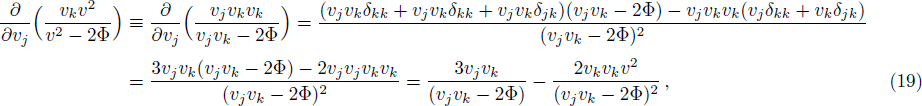
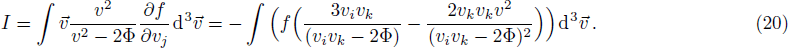
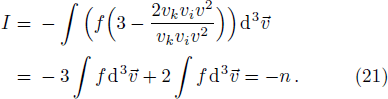
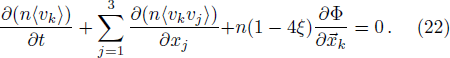
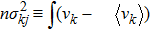
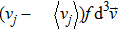
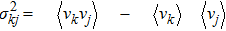
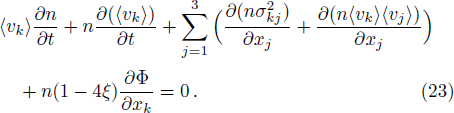
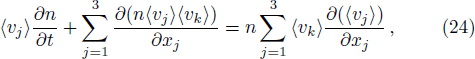
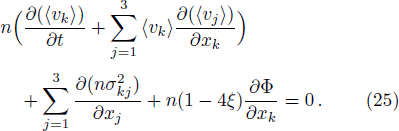
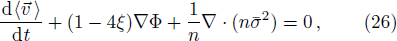
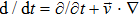
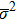
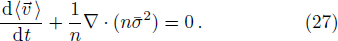
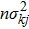

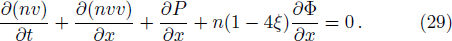

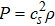
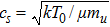
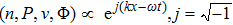
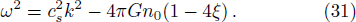
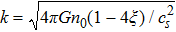
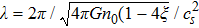
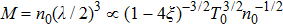
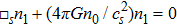
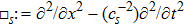
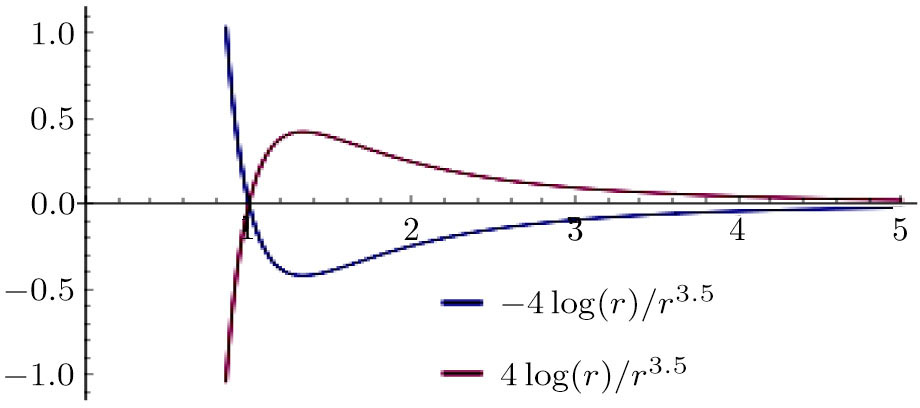
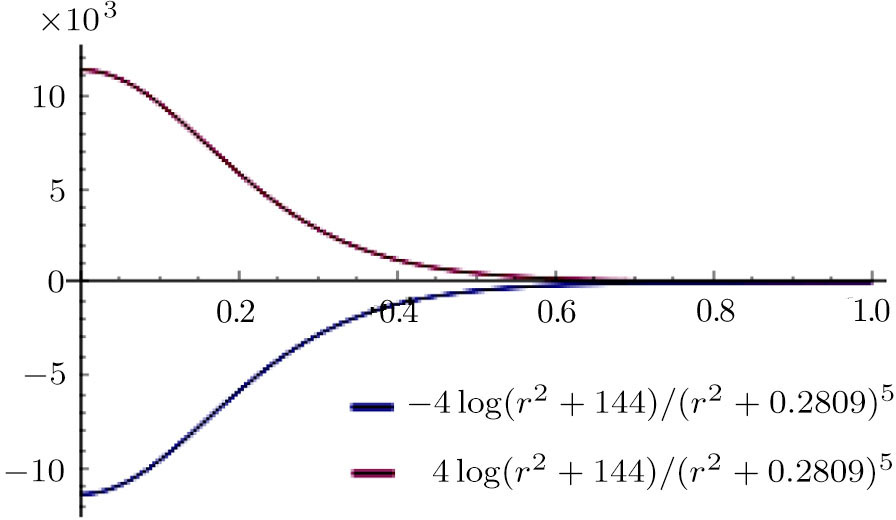
The last term is proportional to the logarithmic of the gravitational field. This is interesting as logarithmic correction to the gravitational field was discussed in differential celestial problems (see the most recent work.[41]) Further that for strong gravitational field the continuity equation is modified. To check this, we can write:
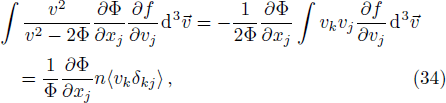
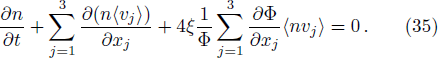
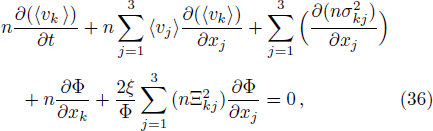
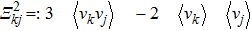
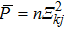
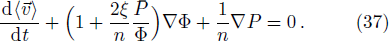
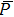
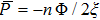
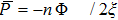
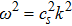
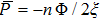
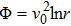
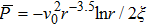
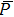
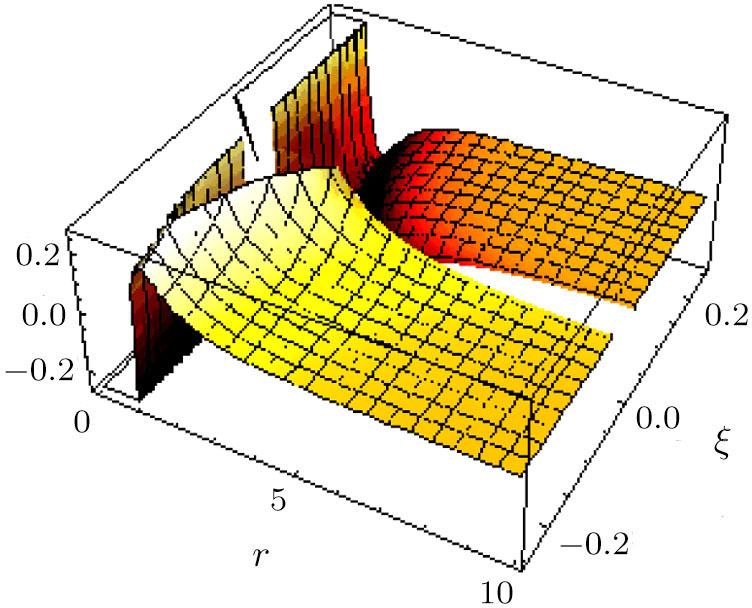
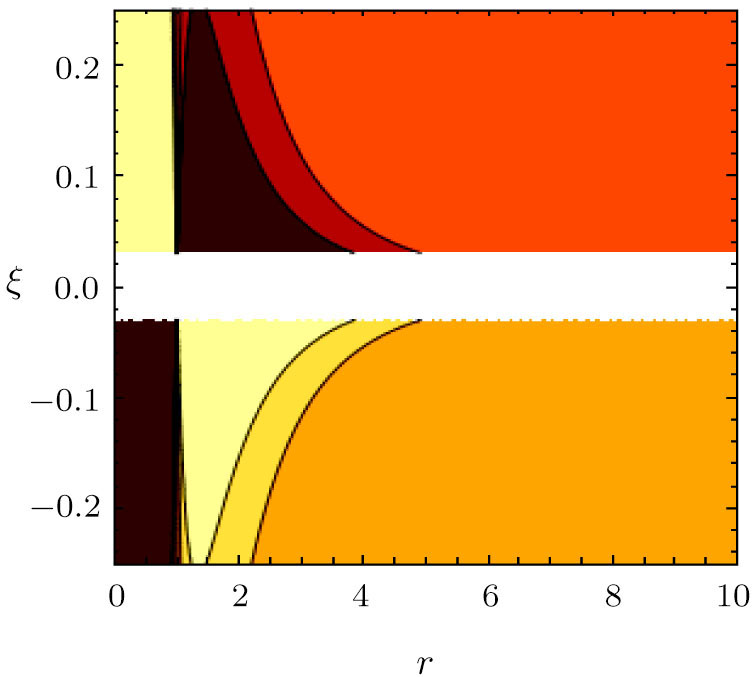
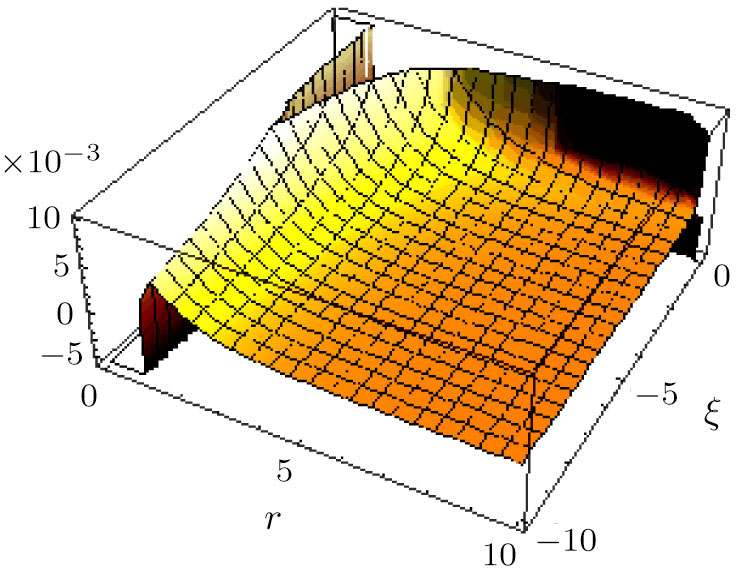
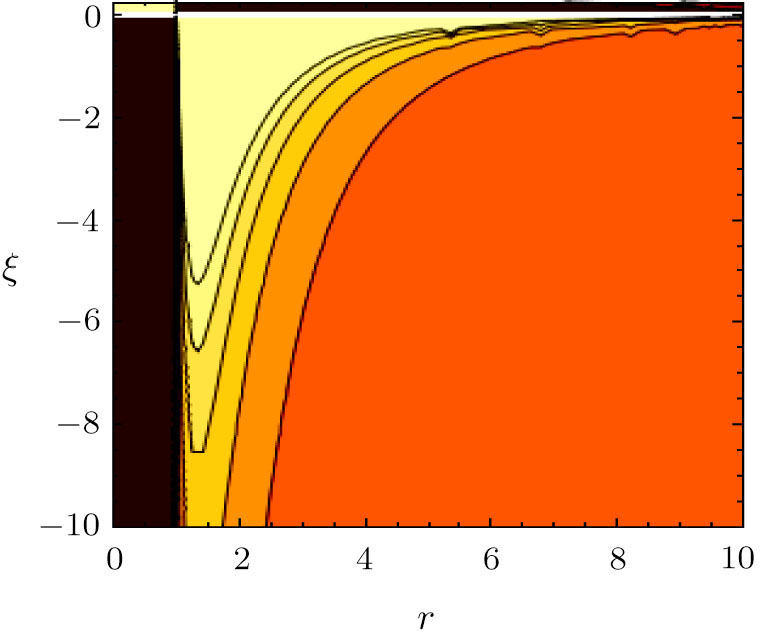
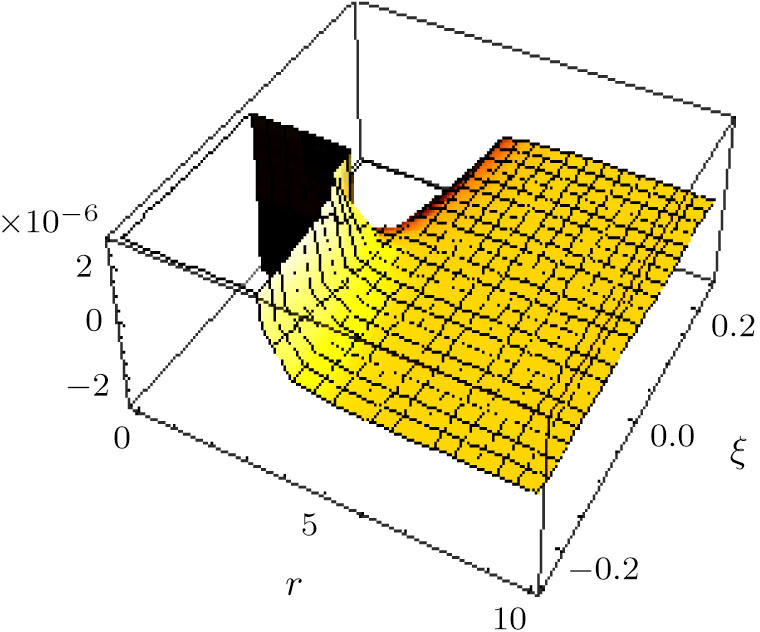
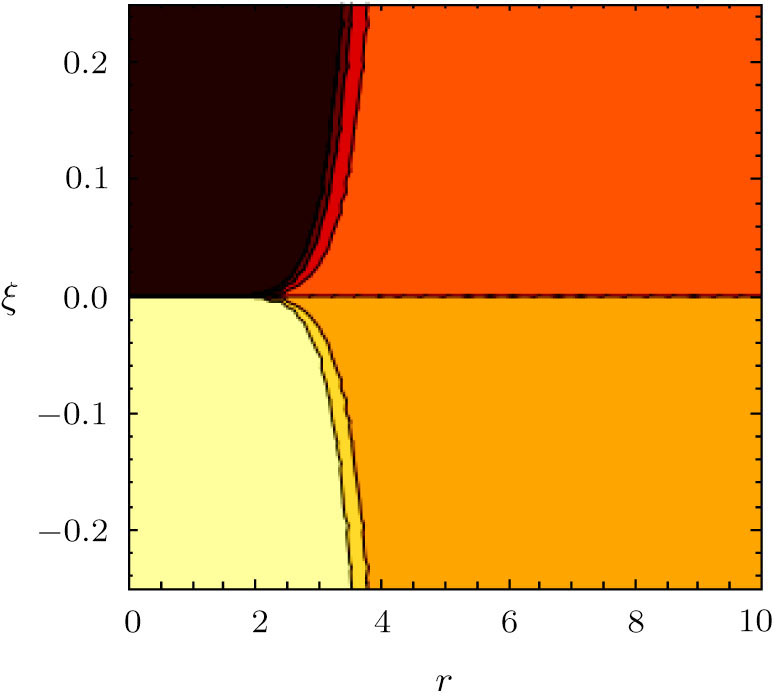
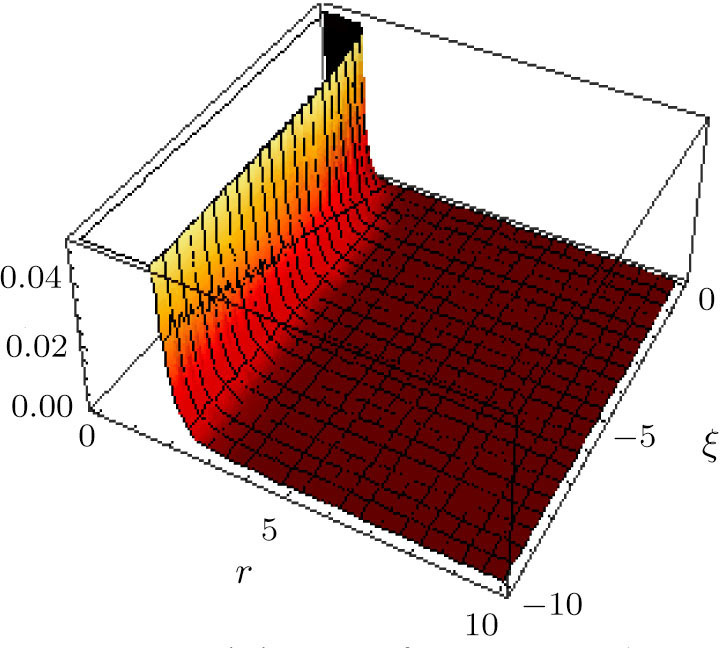
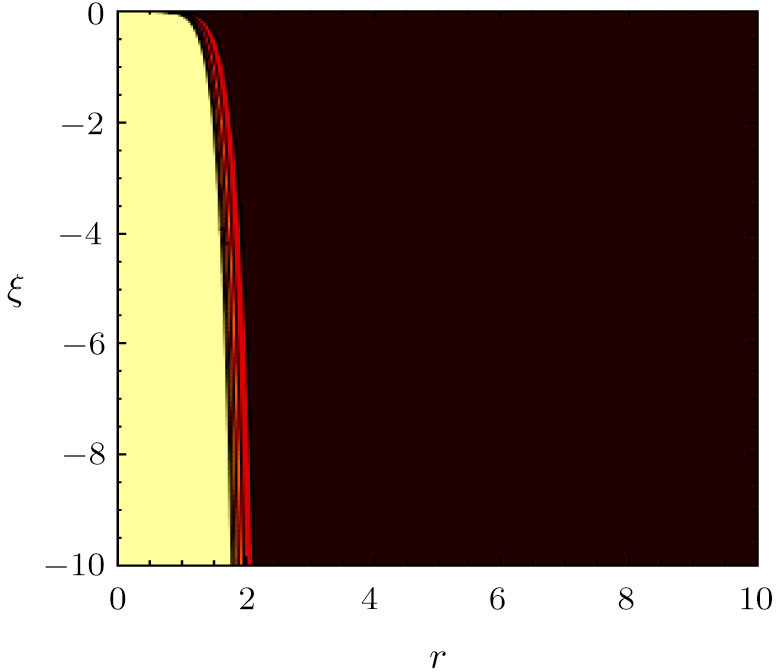
For ξ = 1/8 the global minimum (≈ −8/7e) occurs at r = e2/7 and for ξ = − 1/8 the global maximum (≈ 8/7e) occurs as well at r = e2/7. In Figs. 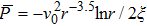
More generally, the dark halo potential of the Milky Way is characterized by the logarithmic potential 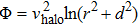
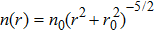
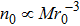
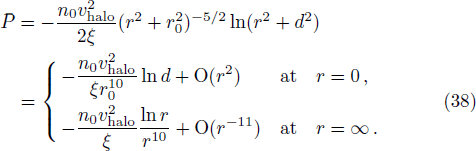
For ξ = 1/8, the global minimum is ≈ − 11367 at r = 0 whereas the global maximum is ≈ 11367 at r = 0 in units vhalo = n0 = 1.
To conclude in this work, we have introduced the notion of LL, which belongs to the class of non-standard Lagrangians. After deriving the corresponding Hamiltonian equations and the modified Boltzmann equation we have discussed their implications in stellar dynamics in galaxies. We have discussed two independent classical cases: the weak and the strong gravitational field. For the weak case, the modified Jeans equations are more or less similar to the standard ones. More precisely, after introducing a small perturbation around the equilibrium position, it was observed that the dispersion relation is slightly modified and depends on the parameter ξ. When ξ = 1/4, the medium is governed by the isothermal sound waves. For ξ > 1/4, the system is stable and the perturbation varies periodically in time. Stability of the system is achieved as well for ξ < 1/4 and k ≫ 1 whereas it is unstable for k ≪ 1. We have deduced as well the Jeans mass and it was observed that a physical solution is obtained only if ξ < 1/4. For the strong case, Jeans equations are modified considerably. A new pressure term 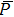
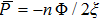
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] |