Cite this Article
Wang Gai-Hua, Zhang Yong-Shuai, He Jing-Song. Dynamics of the Smooth Positons of the Wadati-Konno-Ichikawa Equation. Communications in Theoretical Physics, 2018, 69(3): 227  
Permissions
Dynamics of the Smooth Positons of the Wadati-Konno-Ichikawa Equation
Wang Gai-Hua1, Zhang Yong-Shuai2, He Jing-Song1, †
Department of Mathematics, Ningbo University, Ningbo 315211, China
School of Science, Zhejiang University of Science and Technology, Hangzhou 310023, China

 

† Corresponding author. E-mail: hejingsong@nbu.edu.cn jshe@ustc.edu.cn

Supported by the National Natural Science Foundation of China under Grant No. 11671219, the K. C. Wong Magna Fund in Ningbo University

Abstract
Abstract

We discuss a modified Wadati-Konno-Ichikawa (mWKI) equation, which is equivalent to the WKI equation by a hodograph transformation. The explicit formula of degenerated solution of mWKI equation is provided by using degenerate Darboux transformation with respect to the eigenvalues, which yields two kinds of smooth solutions possessing the vanishing and nonvanishing boundary conditions respectively. In particular, a method for the decomposition of modulus square is operated to the positon solution, and the approximate orbits before and after collision of positon solutions are displayed explicitly.

PACS: ;02.30.Ik;;02.30.Jr;
Keyword:Wadati-Konno-Ichikawa equation;positon;breather-positon;trajectory;phase shift
1 Introduction

Wadati, Konno, and Ichikawa (WKI) derived two highly nontrivial nonlinear equations in 1979.[1] These equations are the WKI-I equation

and the WKI-II equation

Both of them can be related to AKNS system by a series of gauge transformations.[2–3] Recently, by applying hodograph transformation

we find a new kind of equivalent form of the WKI-I equation:[4]

which is called modified WKI (mWKI) equation. Here

Note that Eq. (4a) holds automatically according to Eqs. (4b), (4c), and (5).

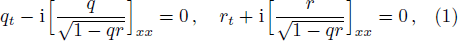
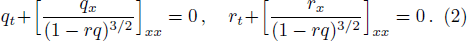
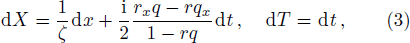
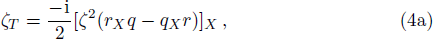
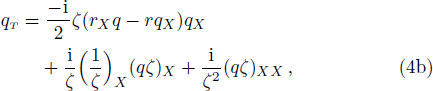
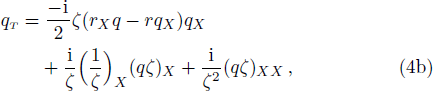
The mWKI equation is a very special equation in integrable systems, because it has bright solitons from vacuum for defocusing system (r = q*, asterisk denoting complex conjugate) and focusing system (r = −q*) simultaneously, which is never displayed until the appearance of our recent work.[4] In addition, the soliton solution, breather solution and rogue wave solutions[4] of the mWKI equation are also constructed by the Darboux transformation (DT). Here, we will study the mWKI equation with degenerated DT[5] and give the formula of N-th order degenerated solution, which yields positon solution and breather-position (b-positon) solution.

Positon solution was first found by Matveev in 1992 for Korteweg de Vries (KdV) equation when the spectral parameters are approaching the same value,[6] then it was quickly extended to the sine-Gordon equation,[7–8] the modified KdV equation,[9–10] sinh-Gordon equation,[11] and so on. Similar to the soliton solution, positon solution is a fundamental solution generated from zero background for nonlinear integrable equation, and exhibits many interesting properties. Even though soliton and positon solutions are different, they also have connections,[12] In general, positon solutions are viewed as long-range analogues of solitons and they are slowly decreasing, oscillating solutions.[13] In addition, relationship between positon solution and breather solution is shown in Ref. [12].

The positon solution belongs to the “Hirota family” and can be derived from the standard second order soliton by a proper limiting procedure.[14] The detailed derivation of a second order positon solution of the KdV equation from a second order soliton solution has been given by Kurasov. Different from the soliton solutions, two positons remain unchanged after mutual collision.[15–16] Since the positon solutions are mainly found in the real-valued equations,[17–19] and these solutions are singular. The mWKI as a complex-valued physical model is deserved to be further studied for the following reasons: (i) Are there smooth positon solutions in the complex-valued equation like the mWKI? (ii) How to calculate the trajectories before and after collisions of positon solutions? (iii) The WKI equation admits saturable nonlinearity, and the b-positon solutions are useful for generating the rogue waves in optics,[20] so the study about b-positon solution of the mWKI has potential value in optics.

2 Degenerated Solutions of the mWKI Equation

The Lax pair of the WKI-I equation[1] is given by

Here

After the action of a hodograph transformation defined by Eq. (3), the Lax pair of the mWKI equation becomes[4]

Here ψ(X, T, λ) is an eigenfunction associated with eigenvalue λ.

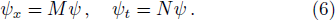
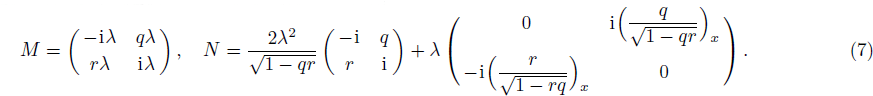
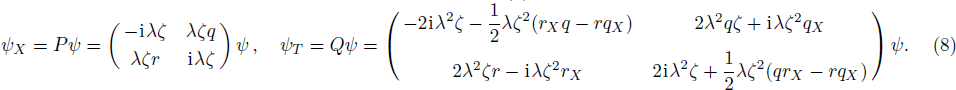
Similar to the determinant representation of the n-fold DT for the nonlinear Schrödinger equation,[21–22] the n-fold DT of the mWKI equation has also been given in a determinant form.[4] For convenience, we display the formula of N-th order solution generated by the n-fold DT and reduction condition in appendix.

Set “seed” solution r = q = 0, then ζ = 1. Furthermore, select λk = ξk + iηk, the eigenfunction associated with the “seed” solution is given by

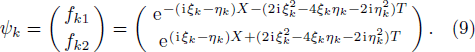
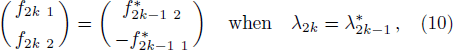
According to the reduction condition r = −q* and the relationship of the different eigenfunctions given in Eq. (A2), we select

then new solutions generated by the n-fold DT satisfy the reduction condition q[n] = −r[n]*.

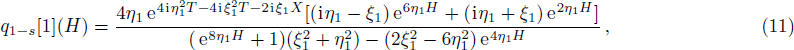
According to reduction condition and the formula of N-th order solution given in Eq. (A1), the first order soliton solution of the mWKI equation is

with H = X + 4ξ1T. This solution has been given in Ref. [4] and it will be used to study the decomposition of positon solutions.

Similar to Ref. [6], when eigenvalues also go to the same value in formulas (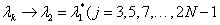A1), i.e., λj → λ1, ; k = 4,6,...,2N), it produces the degenerated solution (or positon), and in this case, the formula given by Eq. (A1) in appendix becomes degenerated. The formulas of N-th order degenerated solution (or positon) of the mWKI equation are obtained by this limit procedure.

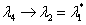
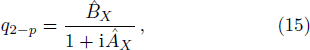
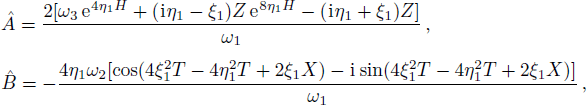
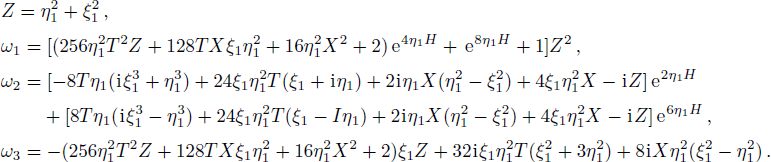
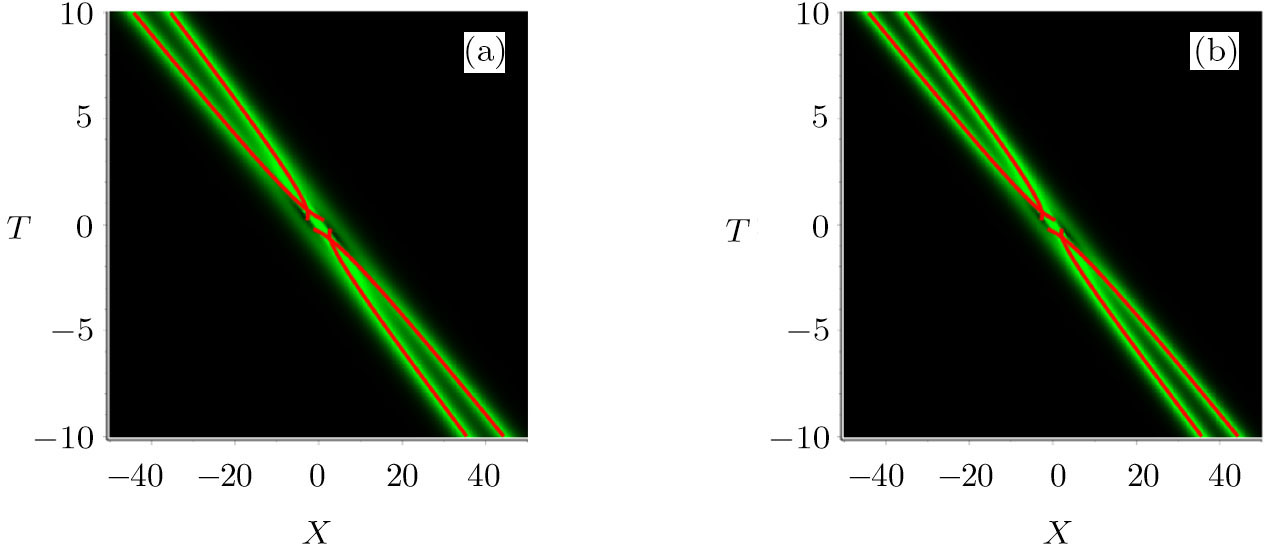
Then, from the formula given in Theorem 1, the fundamental positon (the second order positon) solution is given by setting λ3 → λ1 and , which is in the form of

where

and

The profile of the fundamental positon solution is displayed in Fig. 1. As is well known, trajectories of the second order soliton solutions are two straight lines before and after collision, but there exists a phase shift which is a constant. However, the trajectories of the fundamental positon solutions are two curved lines and the phase shift is an undetermined function of T. In order to get phase shift, we assume the |q2−p|2 can be decomposed as follows:

which is obtained from Eq. (11). Here

Substituting Eq. (17) into Eq. (16), and just considering the approximation in the neighbourhood of H = 0, it yields

which leads to . It is easy to get c1 = ln(T4)/8 when T → ∞. In summary, we get following theorem on the decomposition of the positon.

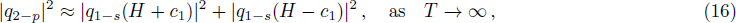
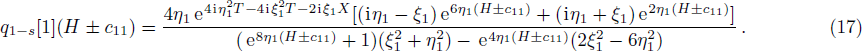
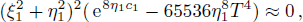
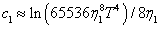
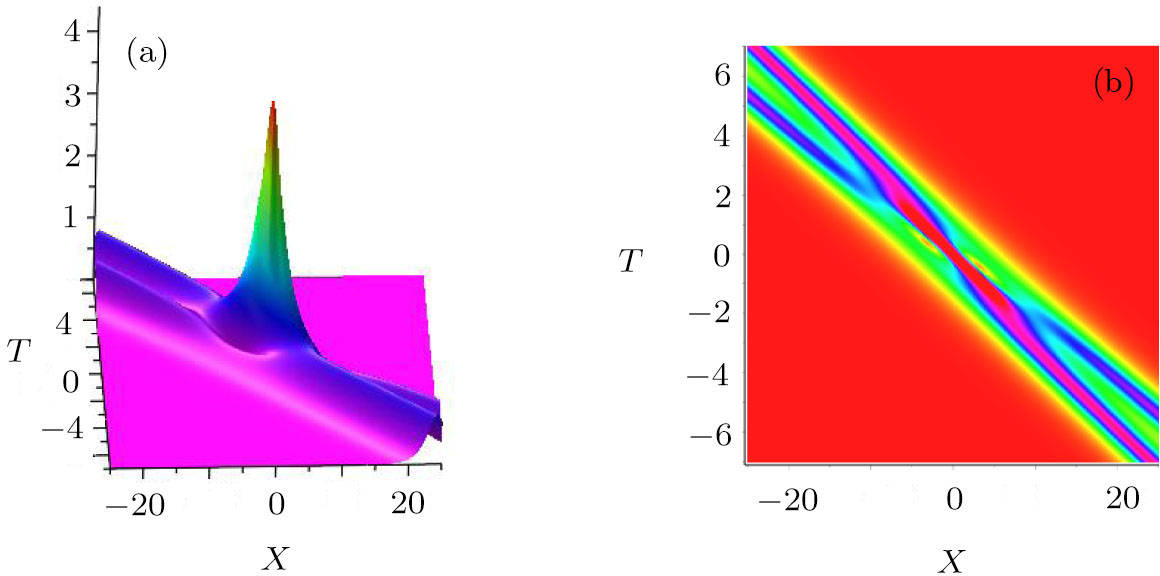Fig. 1 (Color online) The evolution of the fundamental positon solution |q2−p| for the mWKI equation with ξ1 = 1 and η1 = 0.35.

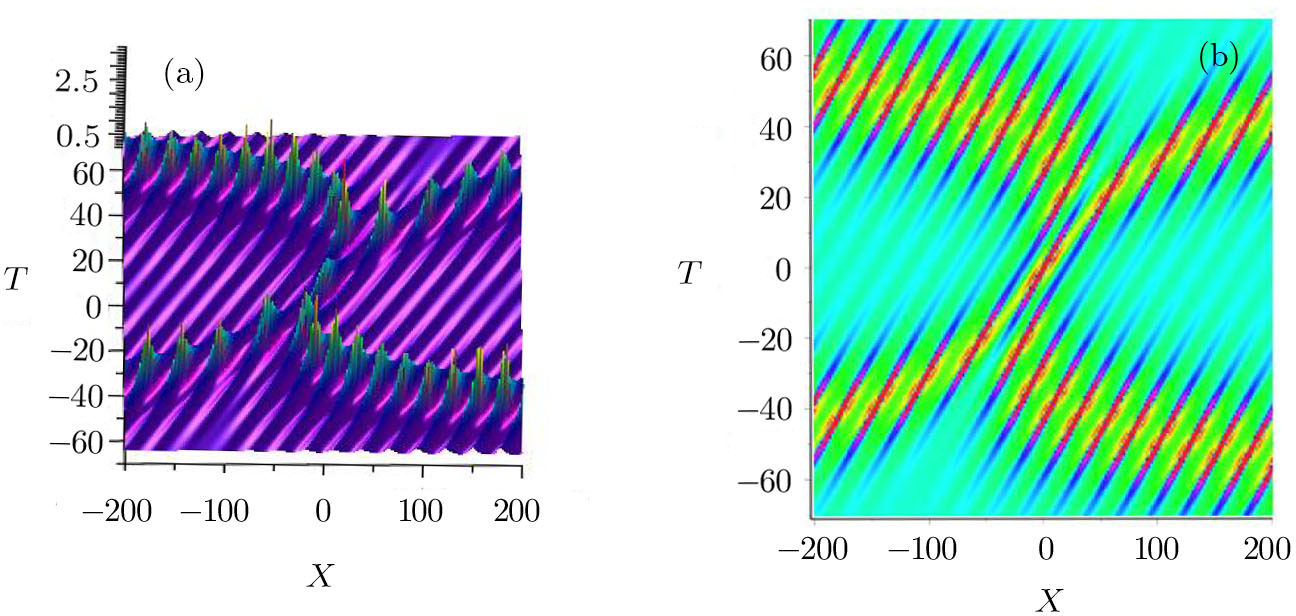
The result given in Theorem 1 is verified by an excellent agreement between the density plot and the approximate orbit of the decomposition in Fig. 2. Actually, in Fig. 2, we display the trajectories of fundamental positon by its density plot (green line), and the approximate orbits derived by the decomposition in red solid line. The red line overlaps the green line very well when T is sufficient large.

Fig. 2 (Color online) The density plot (green line) of the fundamental positon solution |q2−p| for mWKI equation. (a) ξ1 = 1 and η1 = 0.30. (b) ξ1 = 1 and η1 = 0.35. The red solid line denotes the approximate orbit of the decomposition.

Moreover, according to the above decomposition method, we can get the similar results for the higher order positon solutions. In order to further show the validity of this method, we provide another example.

We are now in a position to study the solution of the mWKI equation with a nonvanishing boundary condition. Let a nonzero “seed” solution

then the eigenfunction ψ(λk) is given by

with

Substituting nonzero “seed” solution given in Eq. (18) and eigenfunctions given in Eq. (19) back in to Theorem 1, we can obtain the N-th order b-positon solution of the mWKI equation. The fundamental b-positon solution describes the interaction of two breather solutions, which is similar to the fundamental positon solution that displays the interaction of two solitons in degenerated case. The figures of the b-positon solution are shown in Fig. 3. Further, the higher-order b-positon solution will reduce to a higher-order rogue wave under the parameter conditions A = 1 and C = 1/2 as the appearance of the first order rogue wave.[4]

Fig. 3 (Color online) The dynamic evolution of a fundamental b-postion solution for the mWKI equation with ξ1 = 1, η1 = 0.3.
3 Summary and Discussion

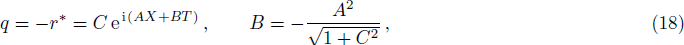
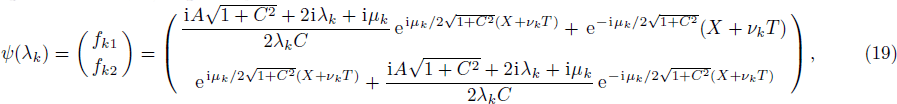
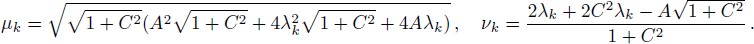
This paper mainly discusses the mWKI equation, which is equivalent to the WKI-I equation by a hodograph transformation. The determinant representation of the N-th order smooth degenerated solution for the mWKI is presented in Theorem 1. According to this representation, formulas of two kinds of degenerated solutions are obtained, i.e., positon solution and b–positon solution. Additionally, based on the decomposition of modulus square, the approximate orbits of the second order positon solution and the third order position solution are given in Corollary 1 and Corollary 2, which overlap trajectories (i.e. density plots) of the positon solutions very well. Moreover, the phase shift in a positon solution is a function of T, which is different from the multi-soliton solution.

Reference
[1] Wadati M. Konno K. Ichikawa Y. H. J. Phys. Soc. Jpn. 47 1979 1698
[2] Wadati M. Sogo K. J. Phys. Soc. Jpn. 52 1983 394
[3] Ishimori Y. J. Phys. Soc. Jpn. 51 1982 3036
[4] Zhang Y. S. Qiu D. Q. Cheng Y. He J. S. Theor. Math. Phys. 191 2017 710
[5] He J. S. Zhang H. R. Wang L. H. et al. Phys. Rev. E 87 2013 052914
[6] Matveev V. B. Phys. Lett. A 166 1992 205
[7] Beutler R. J. Math. Phys. 34 1993 3098
[8] Andreev V. A. Brezhnev Y. V. Phys. Lett. A 38 1995 58
[9] Stahlhofen A. A. Ann. Phys. 504 1992 554
[10] Rasinariu C. Sukhatme U. Khare A. J. Phys. A: Gen. Phys. 29 1996 1803
[11] Beutler R. Positon Solutions of the Sinh-Gordon Equation, in Nonlinear Coherent Structures in Physics and Biology Spatschek K. H. Mertens F. G. Springer-Verlag New York 1994 267 270
[12] Beutler R. Stahlhofen A. Matveev V. B. Phys. Scr. 50 2006 9
[13] Matveev V. B. Theor. Math. Phys. 131 2002 483
[14] Jaworski M. Zagrodziski J. Chaos, Solitons & Fractals 5 1995 2229
[15] Chow K. W. Lai W. C. Shek C. K. Tso K. Chaos, Solitons & Fractals 9 1998 1901
[16] Dubard P. Gaillard P. Klein C. Matveev V. B. Eur. Phys. J. Spec. Top. 185 2010 247
[17] Zhang D. J. Chen D. Y. J. Phys. A: Gen. Phys. 37 2004 851
[18] Wu H. X. Zeng Y. B. Fan T. Y. Commun. Nonlinear Sci. Numer. Simulat. 13 2008 2146
[19] Hu H. C. Liu Y. Phys. Lett. A 372 2008 5795
[20] Wang L. H. He J. S. Xu H. et al. Phys. Rev. E 95 2017 042217
[21] Matveev V. B. Salle M. A. Darboux Transformations and Solitons Springer-Verlag Berlin 1991
[22] He J. S. Zhang L. Cheng Y. Li Y. S. Sci. China Ser. A 49 2006 1867