† Corresponding author. E-mail:
In this work, the simultaneous effects of electric field and impurity on the non-extensive entropy of a GaAs/Ga0.5In0.5As double cone-like quantum dot that is grown on a GaAs wet layer are studied. The system is under an external electric field directed along the −x direction. First, we have solved the Schrödinger equation using the finite element method. Then, we have used the Tsallis formalism and calculated the entropy of the system for different temperatures, electric fields and impurity locations. It is found that the entropy decreases with increasing the electric field and temperature. Since the electric field directed along the −x direction, the entropy reduces when the impurity moves toward the left hand side.
As is well known, electronic and transport properties of quantum dots are quite different from those of the bulk structures. Using novel nanofabrication methods such as molecular beam epitaxy, it is possible to fabricate quantum dots with various geometrical shapes and sizes like spherical, pyramidal, ellipsoidal, lens-shaped, cone-like.[1–4]
In recent years, scientists worldwide have widely focused on the electronic, transport and optical properties of double quantum dots. The various confinement potential models are used for investigating physical properties of double quantum dots. For example, Bejan and Niculescu have studied intense laser effects on the optical properties of asymmetric GaAs double quantum dots under applied electric field.[5] Chen et al.[6] have studied nonlinear optical rectification in asymmetric double triangular quantum wells. Petta et al.[7] have investigated manipulation of a single charge in a double quantum dot. Gorman et al.[8] have studied charge-qubit operation of an isolated double quantum dot. Recently, we have studied third-harmonic generation in a double ring-shaped quantum dot under electron-phonon interaction.[9] To more information, the reader can refer to Refs. [10–13].
During the last few years, main attention has been devoted on the subject regarding the impurity states in nanostructures. Impurity state plays an important role in semiconductor devices as it modulates the electronic properties of nanostructures. It is fully known that the binding energy of a hydrogenic impurity in a quantum well has been studied, for the first time, by Bastard.[14] The effect of impurity states on optical, electronic and transport properties of quantum dots is an interesting subject in nanostructures. The presence of impurity strongly alters the energy spectrum and physical properties of quantum dots. In addition to impurity, other external factors such as electric and magnetic fields, temperature and pressure can also distort asymmetrically the confining potential thus modifying the physical properties of quantum dots.[15–25]
Nano statistical thermodynamics which deals with systems consisting of finite numbers of particles is an extension of classical statistical thermodynamics. For the study of small systems consisting of limited assembly of particles (or nanostructures), one needs to modify classical statistical thermodynamics and obtain the detailed information about interatomic (intermolecular) forces.[26–28] The information determines the arrangement of particles as well as the geometry of these nanostructures. The previous works have been demonstrated that the domain of validity of classical thermodynamics and Boltzmann–Gibbs statistics is restricted and as a result, a good deal of attention has been put to discuss such restrictions.[29–30] This branch of science is called Nanothermodynamic or non-extensive thermodynamic. Nanothermodynamic is an extension of the thermodynamic for macroscopic systems.
Among the thermodynamic properties, the entropy is an important property in the basic sciences such as physics and chemistry. Entropy is an elementary information concept and it shows a measure of the disorder of a system. The prediction of this property is a key factor in the design, development and operation of many industrial processes. So far, many different physical definitions of entropy have been given. As is well known, the most popular entropy is the Shannon entropy which was introduced by Claude E. Shannon in 1948.[31] Examples of other entropies are Renyi, Landsberg–Vedral and Tsallis entropy.[32–34] Hitherto, several works have been performed to predict the entropy in nanostructures using different forms of entropy functions. The reader can refer to Refs. [35–40].
In this work, we first obtain the energy levels of double cone-like quantum dot using finite element method (FEM) in the presence of impurity and applied electric field. Then, we have studied the entropy behavior using Tsallis formalism.
Consider a cone-like double quantum dot in which a hydrogenic donor impurity located at the position r0. The system is under an external electric field with magnitude F and directed along the −x direction. Within the effective mass approximation, the Hamiltonian of the system is given by
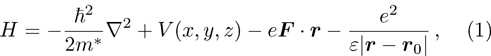
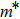
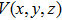
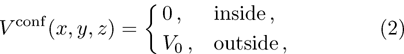
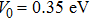
Due to the complicated form of the confinement potential and the presence of impurity, the calculation of energy levels and wave functions, analytically, is a nontrivial task.[41] Therefore, we are interested in employing the finite element method (FEM) to find wave functions and energy levels of the system.[42] Using FEM, we can get a solution when we have a complicated form for the confinement potential and external effects such as impurity, temperature, and applied electric and magnetic fields. In the following, we briefly present the FEM to solve the Schrödinger equation in the Cartesian coordinates.
The finite element method (FEM) is a powerful computational technique to obtain approximate solutions of boundary value problems in basic sciences like engineering, physics, and chemistry.[43–45] We consider a volume of some material or materials having known physical properties. The volume represents the domain of a boundary value problem to be solved. We construct a grid in real space using a discrete number of points. The eigenvalues and eigenvectors of the electrons confined in a quantum dot are evaluated solving the Schrödinger equation
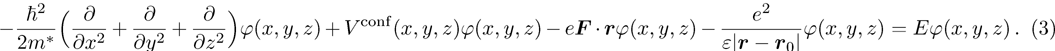
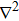
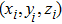
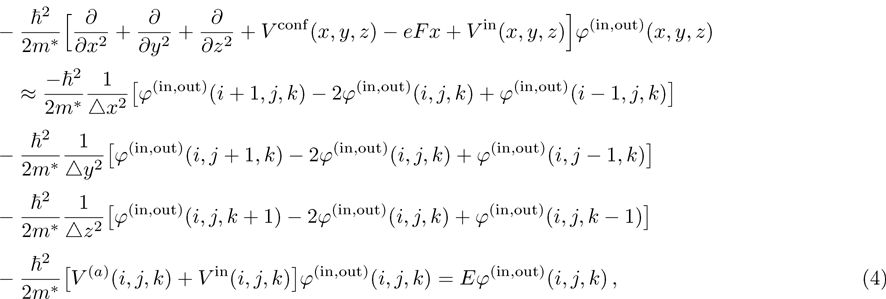
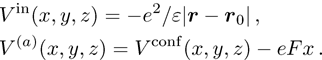
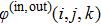
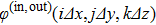
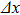
The continuity of the wave functions on the quantum dot boundary is expressed by
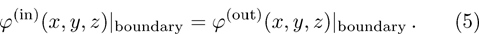
The derivative of wave functions on the quantum dot boundary is defined as:
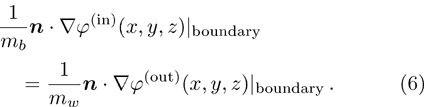
To overcome the restriction of classical thermodynamics and Boltzmann–Gibbs statistics, Tsallis suggested for the first time a generalized version of Boltzmann–Gibbs (BG) statistical mechanics using a new entropic form.[34] This entropy is known as an “entropy of degree q” and depends upon a specific parameter q (nonextensive parameter). It is an interpolation formula that connects the Boltzmann and Gibbs entropies as the parameter q. The Tsallis entropy is given by
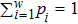
In this section, using the Tsallis formalism, the entropy is computed numerically for the double cone-like quantum dot. The parameters are used in our calculations are: q = 0.9, 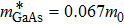
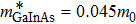
Figure
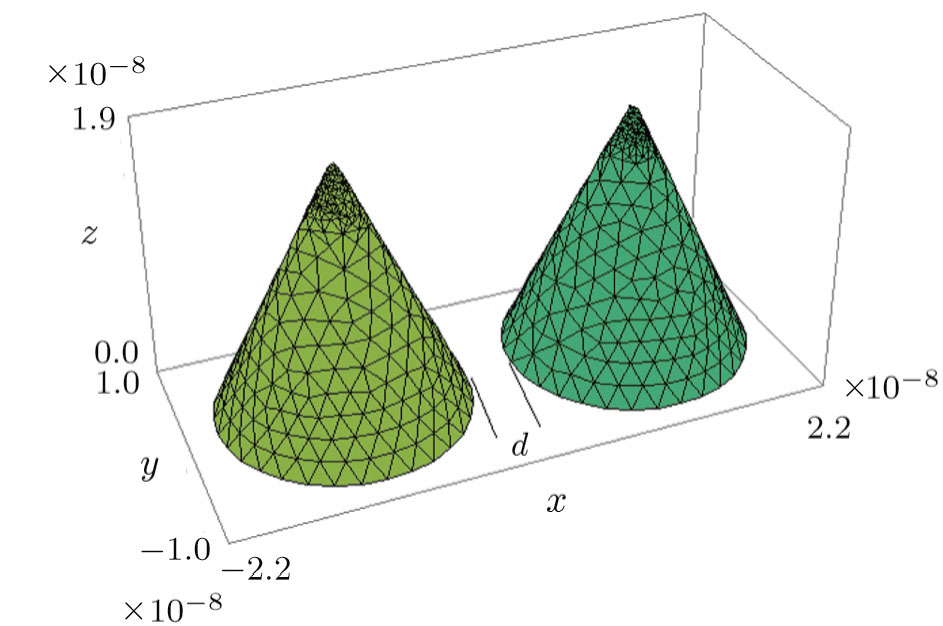 | Fig. 1 (Color online) Schematic diagram of a GaAs/Ga0.5In0.5As double cone-like quantum dot that is grown on a GaAs wet layer. |
Figures 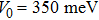
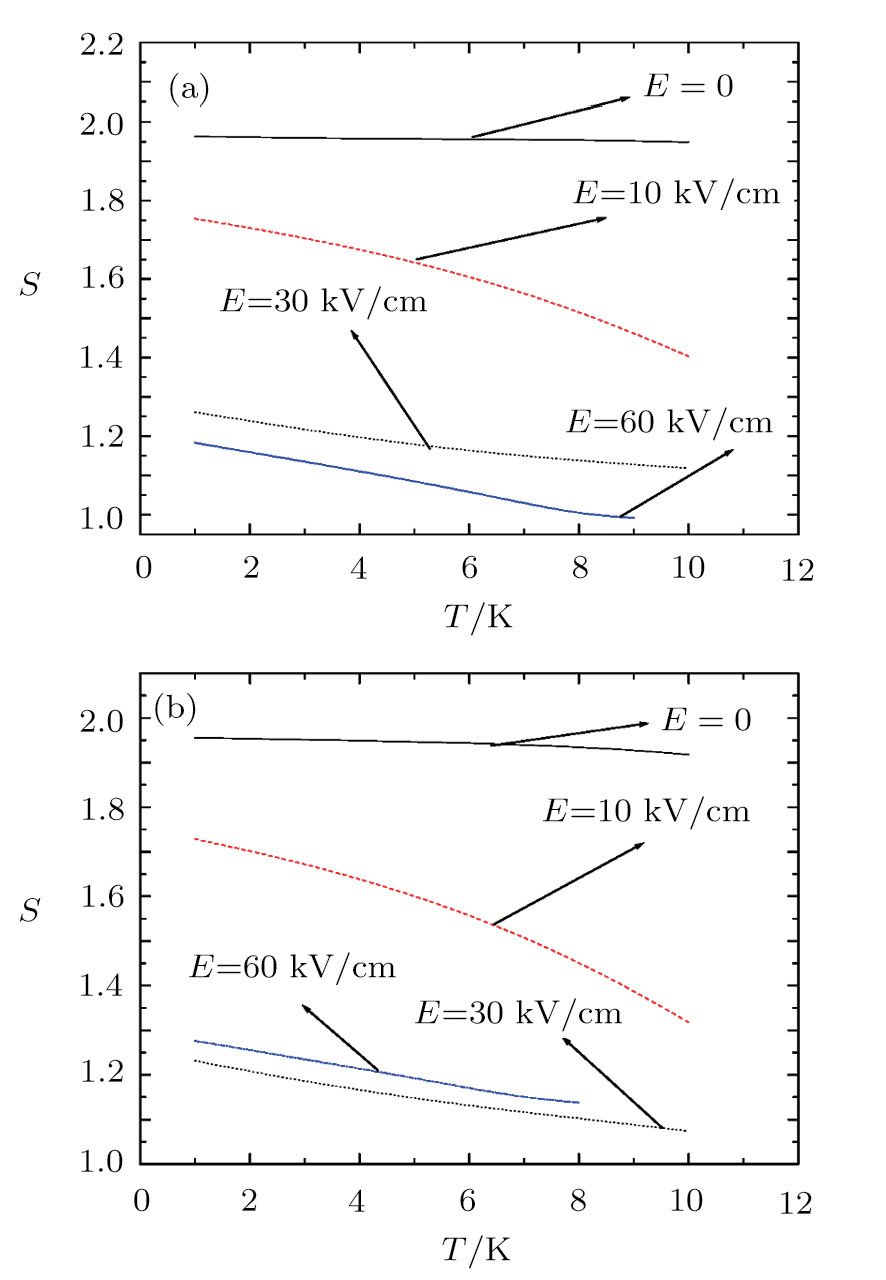
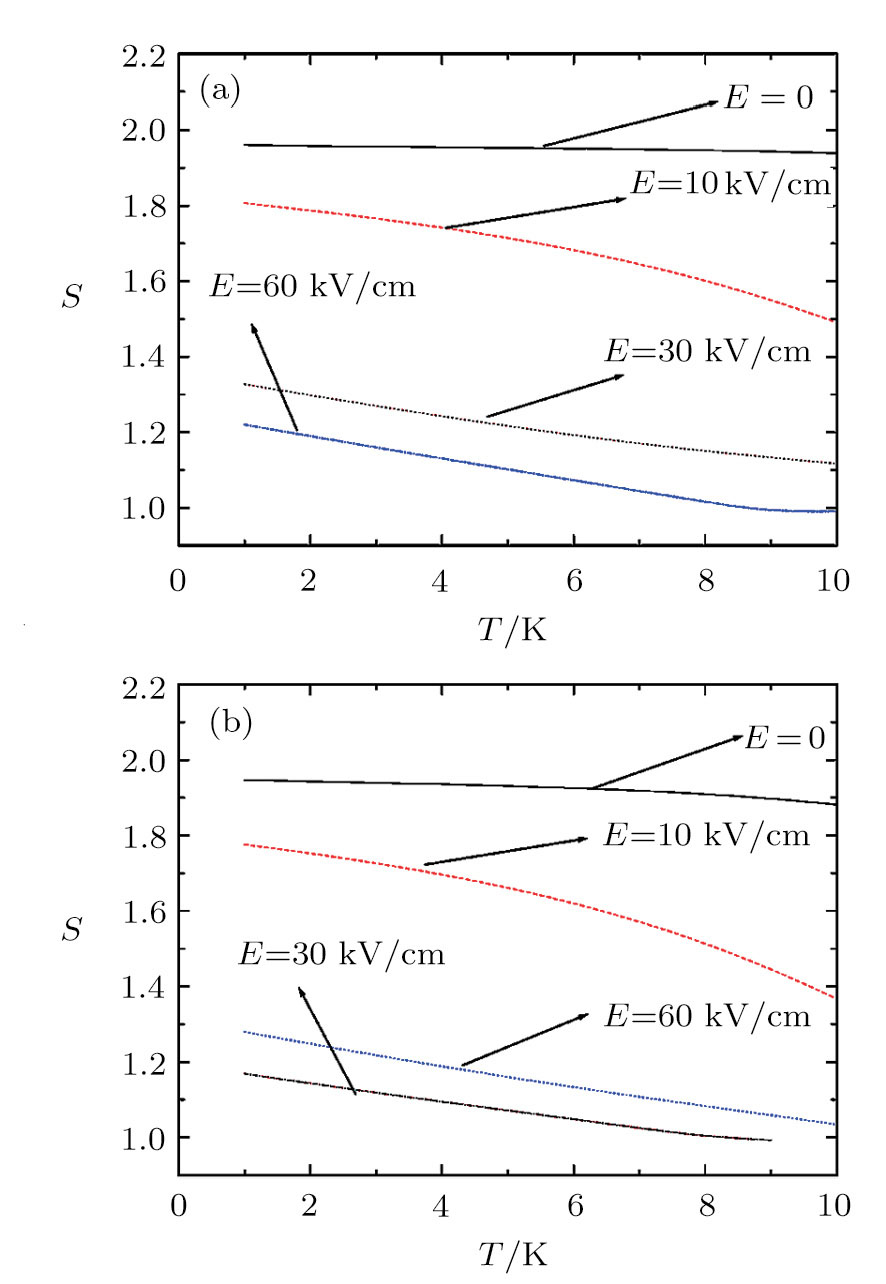 | Fig. 2 (Color online) The entropy as a function of the temperature (a) without and (b) with central impurity for d = 0. |
In Figs. 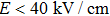
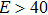
In Fig.
Figure
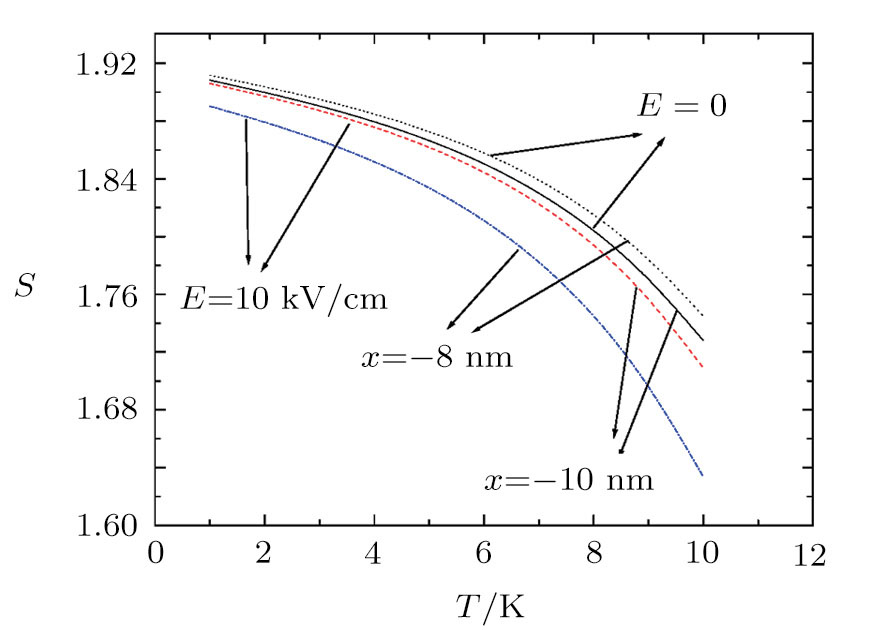
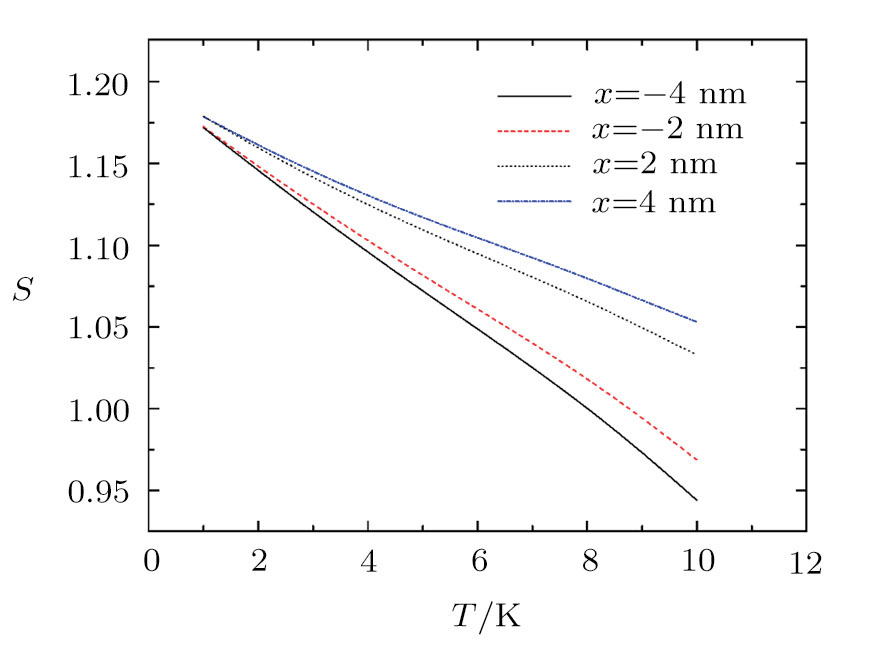
To show the effect of impurity position on the entropy, we have plotted the entropy as a function of impurity location in Fig.
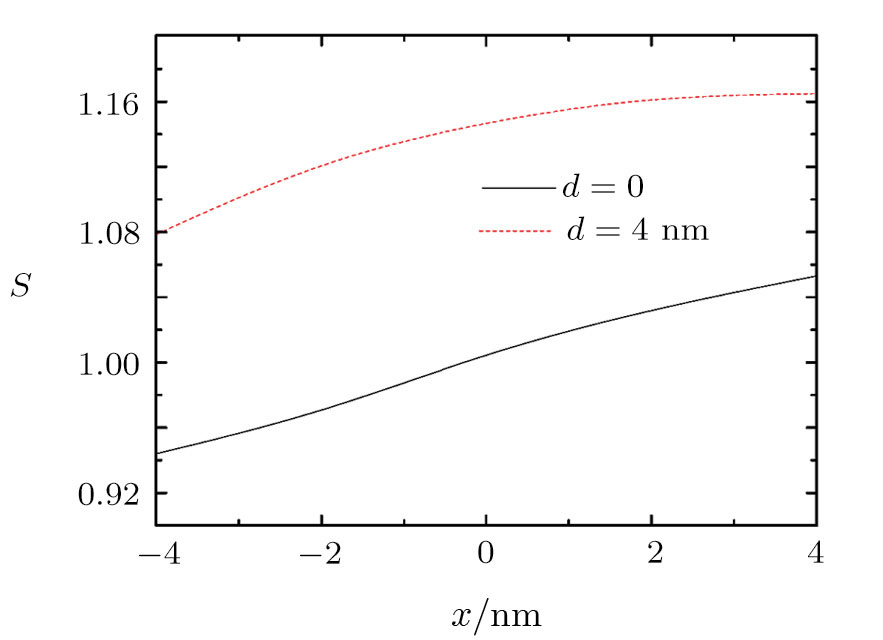 | Fig. 6 (Color online) The entropy as a function of the impurity position for E = 40 kV/cm and T = 10 K. |
Figures
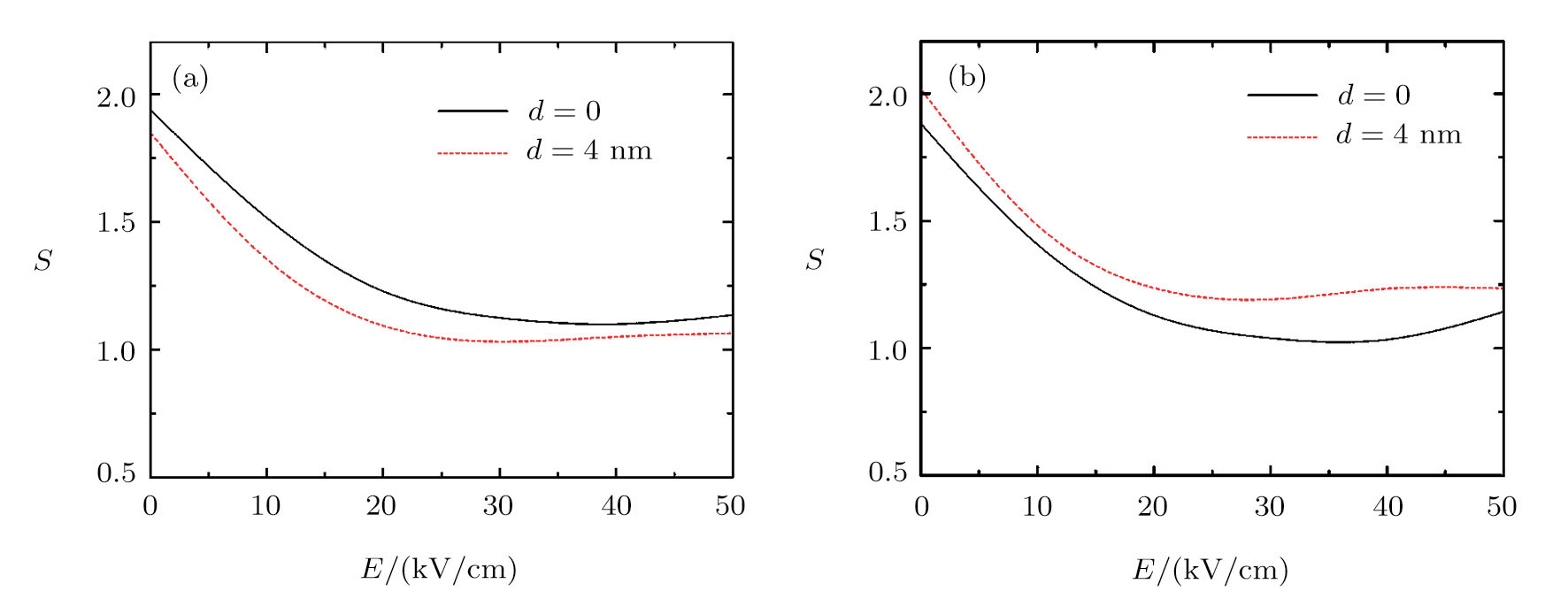 | Fig. 7 (Color online) The entropy as a function of the electric field (a) without and (b) central impurity for T = 10 K. |
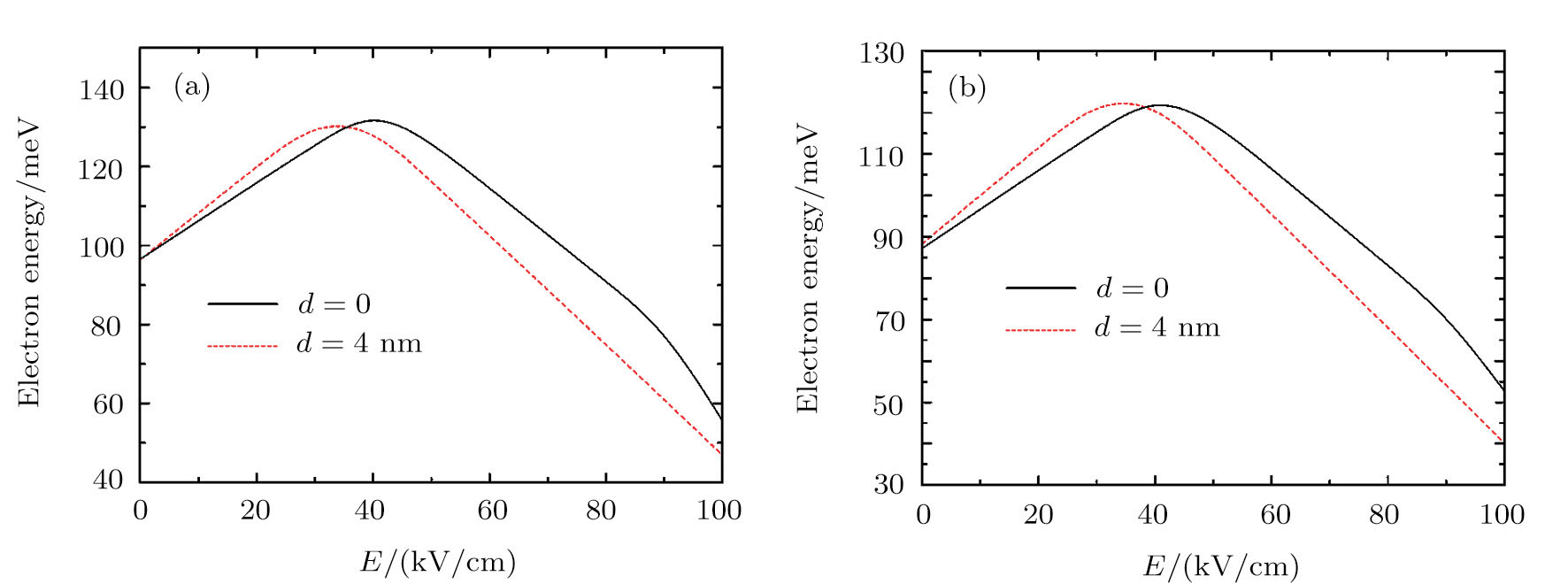 | Fig. 8 (Color online) The energy as a function of the electric field (a) without and (b) central impurity for T = 10 K. |
In Figs.
We have studied the effects of the electric field and impurity on entropy behavior of a double cone-like quantum dot. In this regard, we have first solved the Schrödinger equation using the finite element method. Then, we have employed the Tsallis formalism to study entropy behavior in this system. The results show that the entropy decreases with increasing the temperature for constant impurity position and electric field. Also, the entropy reduces with increasing the electric field. The entropy is decreased with changing impurity position toward the left hand side due to the orientation of applied electric field. Tsallis formalism shows that at relatively lower temperatures like 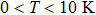
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] |