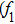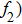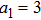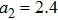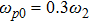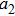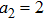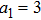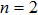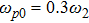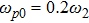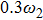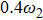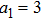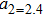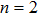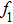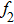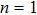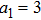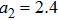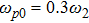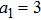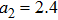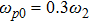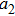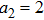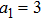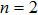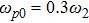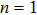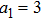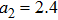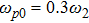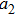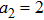† Corresponding author. E-mail:
This paper presents propagation of two cross-focused intense hollow Gaussian laser beams (HGBs) in collisionless plasma and its effect on the generation of electron plasma wave (EPW) and electron acceleration process, when relativistic and ponderomotive nonlinearities are simultaneously operative. Nonlinear differential equations have been set up for beamwidth of laser beams, power of generated EPW, and energy gain by electrons using WKB and paraxial approximations. Numerical simulations have been carried out to investigate the effect of typical laser-plasma parameters on the focusing of laser beams in plasmas and further its effect on power of excited EPW and acceleration of electrons. It is observed that focusing of two laser beams in plasma increases for higher order of hollow Gaussian beams, which significantly enhanced the power of generated EPW and energy gain. The amplitude of EPW and energy gain by electrons is found to enhance with an increase in the intensity of laser beams and plasma density. This study will be useful to plasma beat wave accelerator and in other applications requiring multiple laser beams.
Laser driven plasma-based accelerators are of great interest because of their ability to sustain extremely large acceleration gradients.[1–4] They have widespread applications in various fields such as particle physics, materials science, medicine (ranging from x-ray diagnostics to particle beam therapies), manufacturing industry and to produce extremely short electron bunches. In laser plasma interaction, various schemes are operative for particle acceleration such as laser wakefield accelerator (LWFA),[5–7] plasma beat wave accelerator (PBWA),[5, 8] multiple laser pulses,[9–10] self-modulated LWFA[11–12] etc. in which very high intense laser beams are used. The key requirement for achieving higher acceleration is the large amplitude of the electron plasma wave. A large amplitude plasma wave (with phase velocity near the speed of light) is driven by intense laser pulse in which plasma electrons can be trapped and accelerated to relativistic energies. Therefore, the excitation of electron plasma wave by intense laser beams in plasmas has been an active field of research for charged particle acceleration.
There has been significant interest in the beat wave excitation of electron plasma wave and its application in plasma based particle accelerators. The plasma beat-wave accelerator scheme is one of the most mature methods for plasma acceleration in laser plasma interaction.[5] In this scheme, two intense laser beams of slightly different frequencies ω1 & ω2 and corresponding wave numbers k1 & k2 are used to resonantly excite an electron plasma wave. The resonance conditions for beat wave excitation of electron plasma wave are: 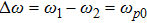
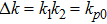
It has been observed that the focusing of laser beams in plasma and the yield of electron acceleration depends on the spatial profile of laser beams and the nonlinearities associated with plasma. Most of the earlier investigations on excitation of electron plasma wave and electron acceleration have been carried out by taking Gaussian intensity distribution of laser beams with ponderomotive/relativistic nonlinearity. In contrast with Gaussian profile of laser beams, currently, the hollow Gaussian intensity profile of laser beams with minimum field intensity at the center has attracted much more attentions because of their unique physical properties and applications.[38–40] The main feature of considered hollow Gaussian laser beams is having the same power at different beam orders with null intensity at the centre. The propagation dynamics of hollow Gaussian beams (HGBs) have been widely studied both experimentally and theoretically.[41–46] Various techniques[47–50] have been used to generate HGBs. These beams can be expressed as a superposition of a series of Lagurerre-Gaussian modes.[41] Moreover, when an ultra-intense laser beams propagates in plasma, both relativistic and ponderomotive nonlinearities arise simultaneously due to electron mass variation and electron density perturbations respectively, which depend on the time scale of the laser pulse.[51–52] Therefore, in comparison with only relativistic/ponderomotive nonlinearity, the dynamics of the propagation of laser beams in plasma is expected to be drastically affected by cumulative effects of relativistic-ponderomotive nonlinearity. It is also important to mention that the relativistic effect and ponderomotive nonlinearity contribute to focusing on a femtosecond time scale at very high intensity. Cross-focusing of HGBs with relativistic/ponderomotive or relativistic-ponderomotive nonlinearities in plasma have been investigated in detail[53–55] but no one has studied the excitation of EPW and electron acceleration. Moreover, donut wakefields generation for particle acceleration by Laguerre-Gaussian laser pulses (carrying a finite amount of orbital angular momentum) using particle-in-cell simulations have also been reported in under-dense plasma.[56–57]
In the present study, we have considered the propagation of two intense hollow Gaussian beams in collisionless plasma. The intensity distribution of the beams along the axis is zero and the maximum is away from the axis. We have studied the cross-focusing of two intense hollow Gaussian laser beams in collisionless plasma with relativistic and ponderomotive nonlinearities and further its effect on the excitation of EPW and electron acceleration. The paraxial-ray approximation[58–59] is used to describe the focal region of the laser beam where all the relevant parameters correspond to a narrow range around the maximum irradiance of the HGBs. Section
We consider two intense linearly polarized co-axial hollow Gaussian laser beams of frequencies ω1 and ω2 propagating along the z-direction in the collisional plasma. The initial electric field distribution of the beams are given by
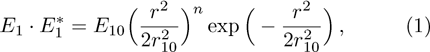
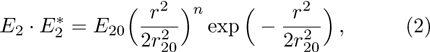

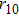
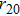
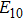
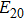
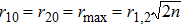
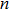
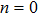
For hollow Gaussian laser beams, transforming the 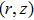
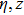
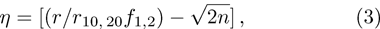
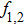
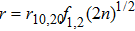
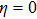
The ponderomotive force acting on the electrons in the presence of relativistic nonlinearity is given by[52–53]
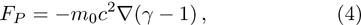
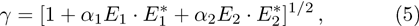
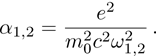
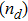
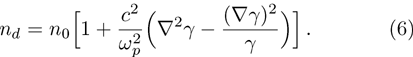
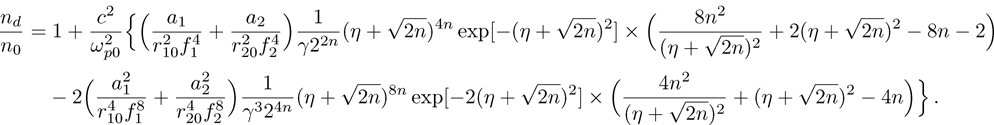
Here 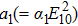
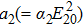
The dielectric constant of the plasma is given by
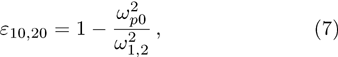
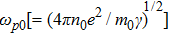
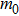
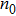
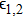
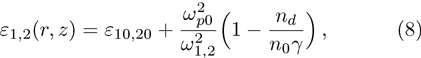
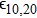
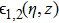
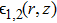
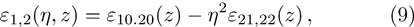
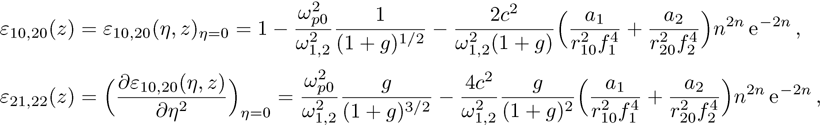
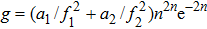
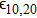
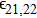
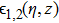
The wave equation governing the electric vectors of the two laser beams in plasma can be written as
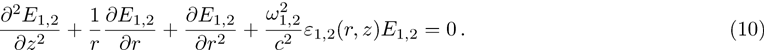
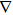
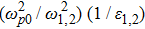
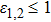

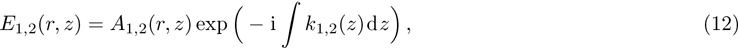
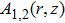
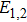
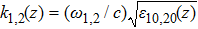
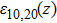
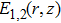
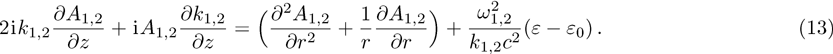
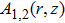
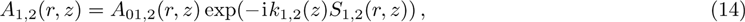
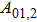
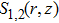
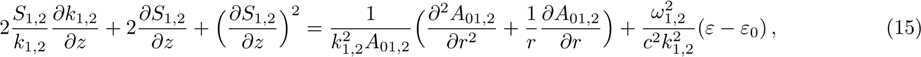
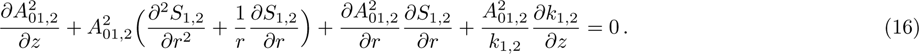
In the paraxial approximation i.e. when 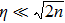
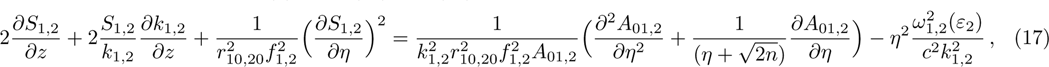
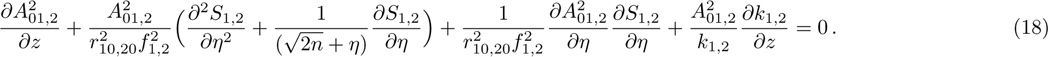
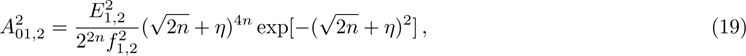

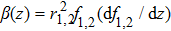
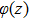
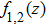
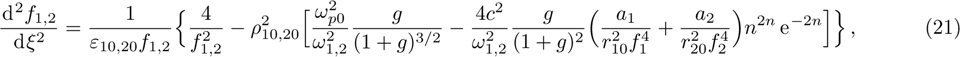
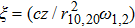
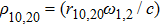
Due to beating of two hollow Gaussian laser beams in plasma and modification in plasma density via relativistic-ponderomotive force, electron plasma wave (EPW) is generated. In this process, the contribution of ions is negligible because they only provide a positive background, i.e., only plasma electrons are responsible for excitation of EPW. The amplitude of electron plasma wave (which depends on the background electron density) gets strongly coupled to the laser beams. To study the effect of relativistic and ponderomotive nonlinearities on the generation of the plasma wave by the beat wave process in paraxial region, we start with the following fluid equations:
(i) The continuity equation:

(ii) The momentum equation:
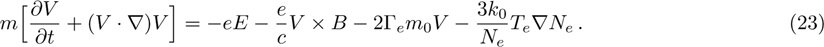
(iii) Poisson’s equation:

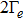
Using Eq. (
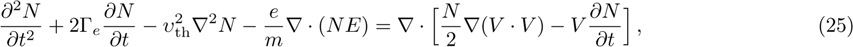
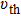
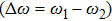
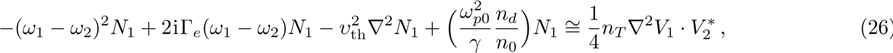
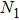
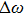
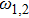
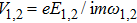
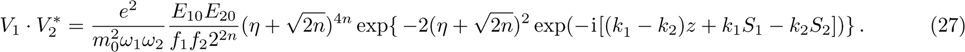
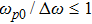
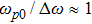
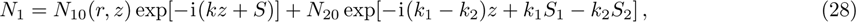
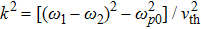
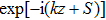
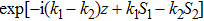
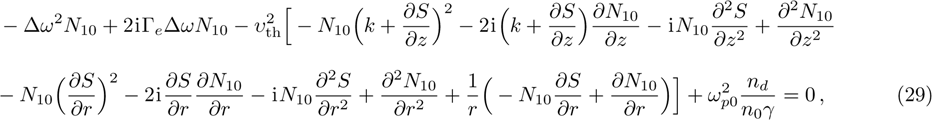
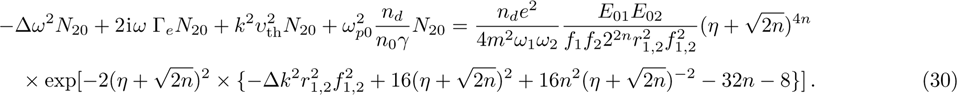
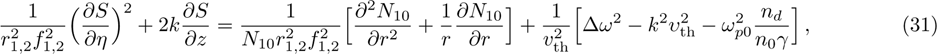
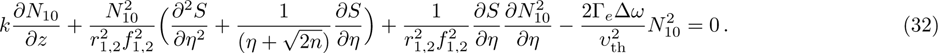
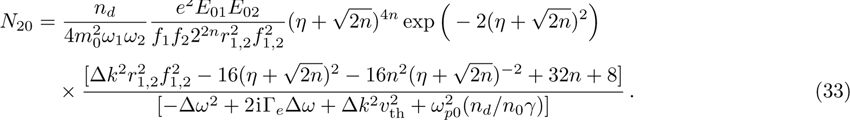
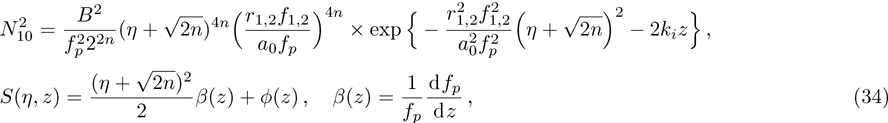
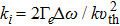
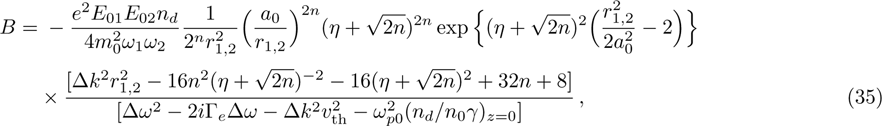
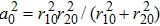
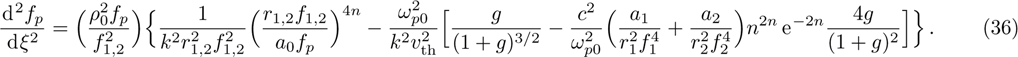
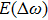
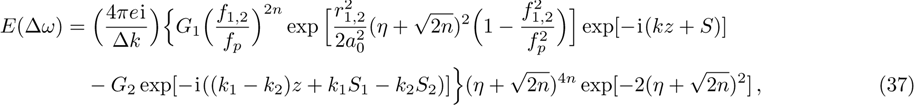
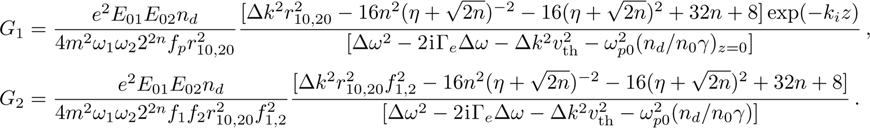
The power associated with electron wave is given by[29]
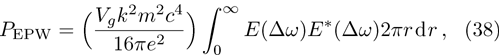
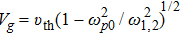
The excited electron plasma wave transfers its energy to accelerate the electrons at the difference frequency of laser beams. The equation governing electron momentum and energy are
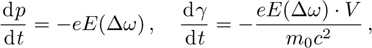
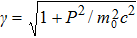
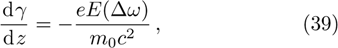
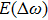
In order to study the cross-focusing of two intense hollow Gaussian laser beams in collisonal plasma with dominant relativistic-ponderomotive nonlinearity and its effect on the generation of electron plasma wave and electron acceleration in paraxial-ray approximation, numerical computation of Eqs. (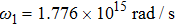
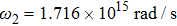
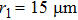
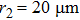
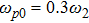
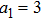
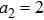
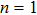
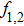
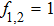
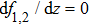
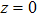
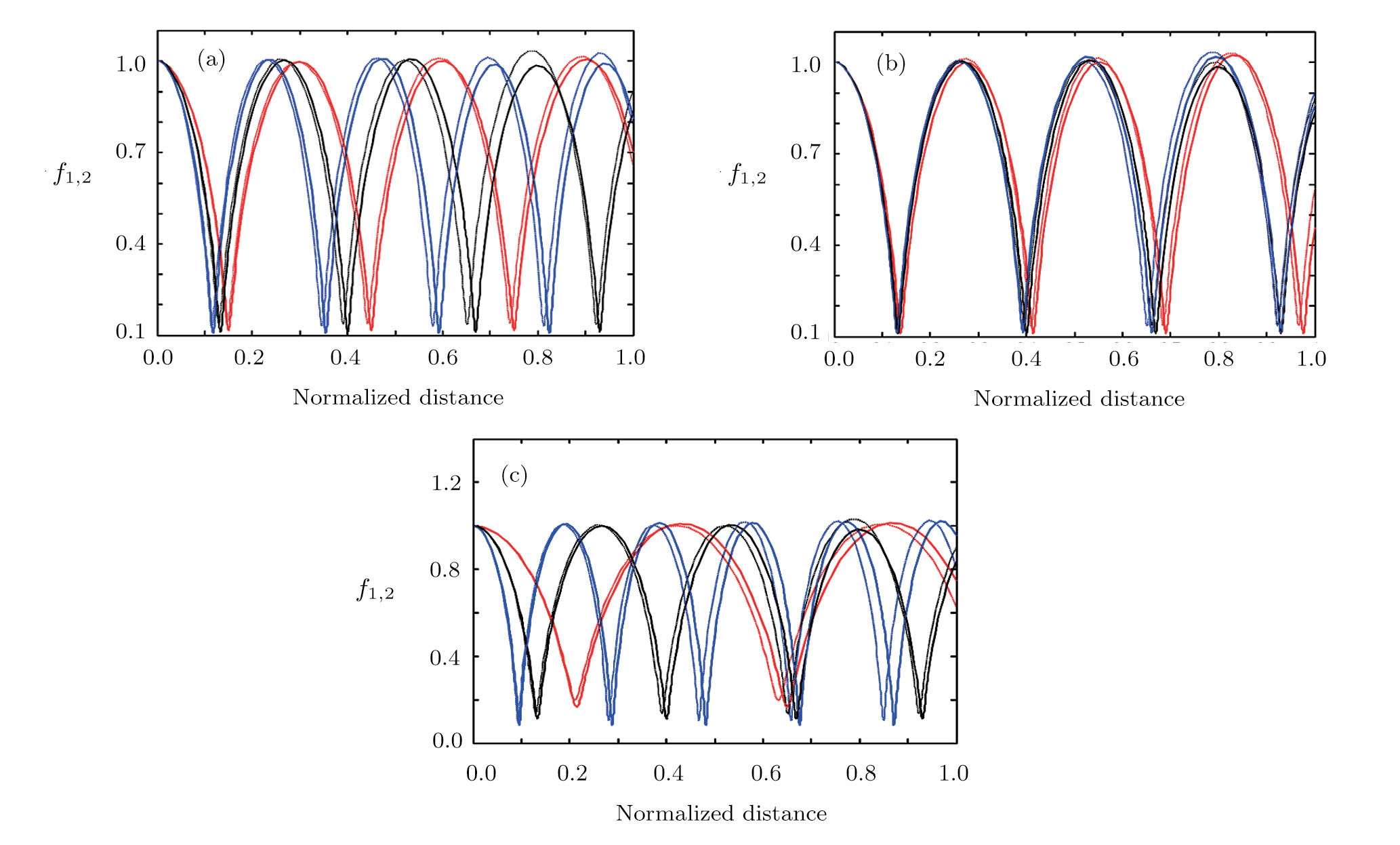
When two intense hollow Gaussian laser beams of slightly different frequencies simultaneously propagate through the plasma, the background electron density of plasma is modified due to ponderomotive force. Equation (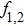
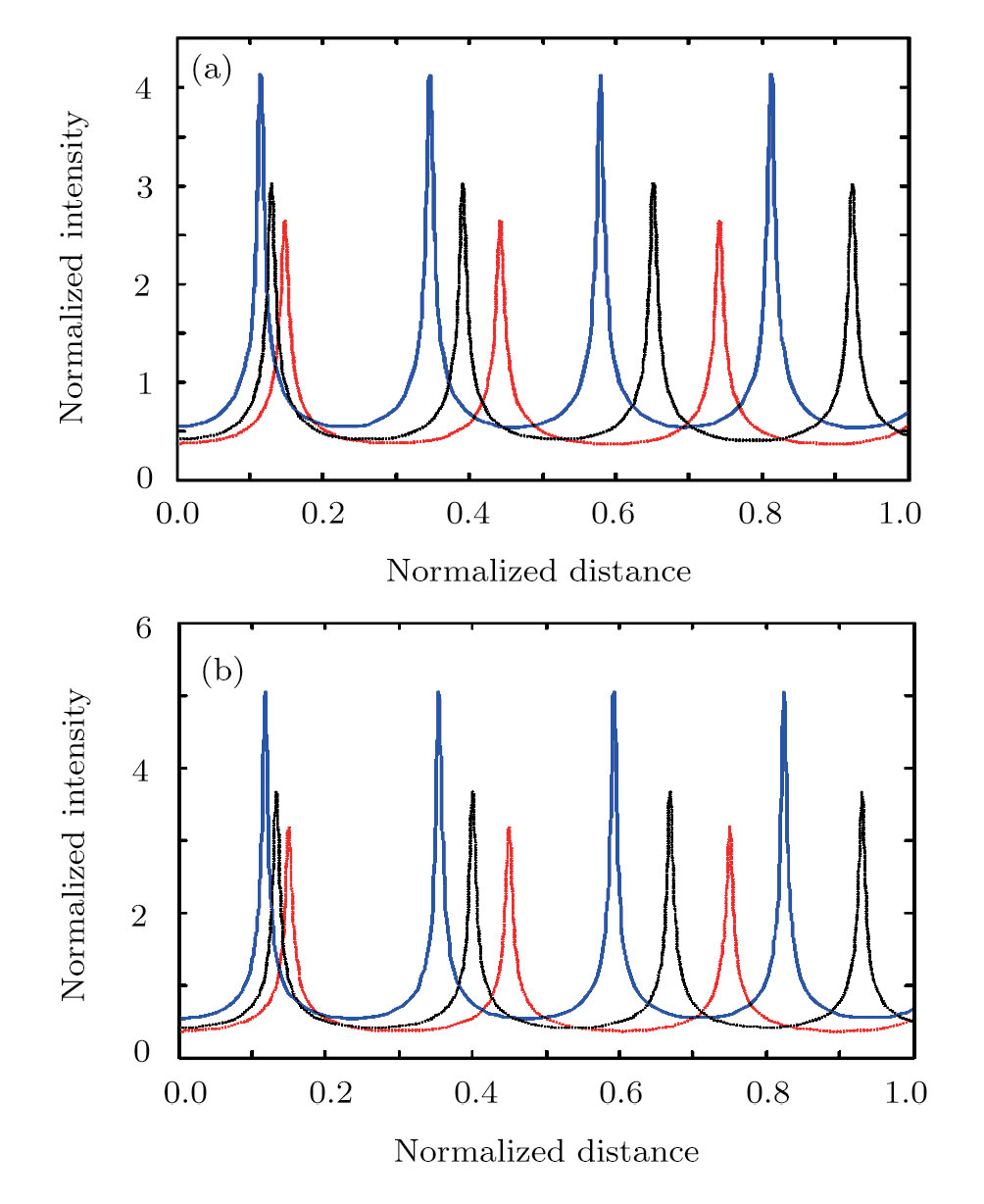
The results of Eqs. (
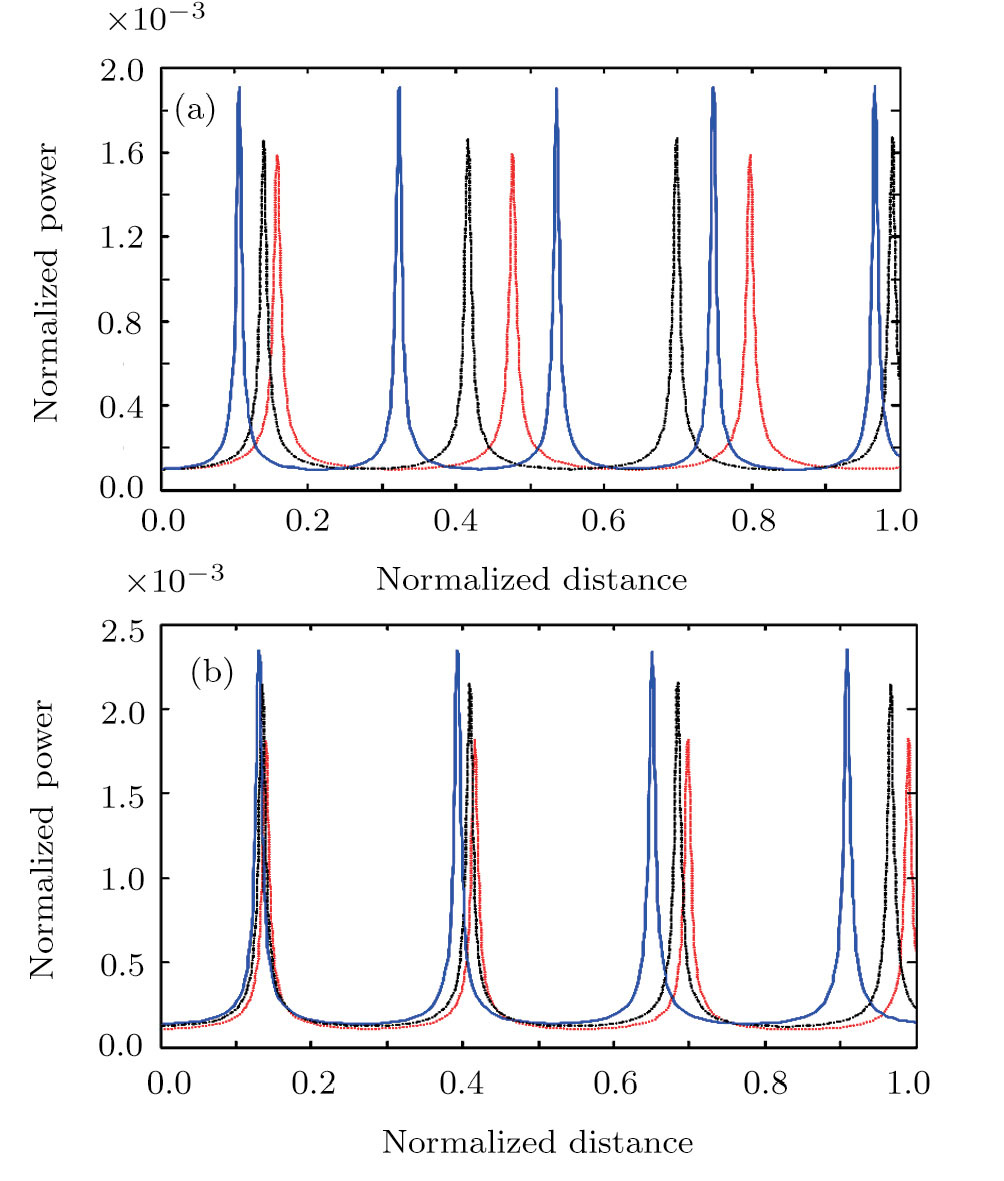
To see the effect of cross-focusing of two intense hollow Gaussian laser beams on the generation of electron plasma wave, we have studied the excitation of the electron plasma wave by the beat wave process in the presence of relativistic and ponderomotive nonlinearities. It is important to mention here that beating between two co-propagating intense laser beams in plasma can generate a longitudinal electron plasma wave with a high electric field and a relativistic phase velocity. The beat plasma wave is very efficient for electron acceleration up to ultrarelativistic energies. Equation (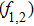
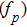
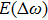
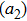
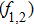
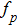
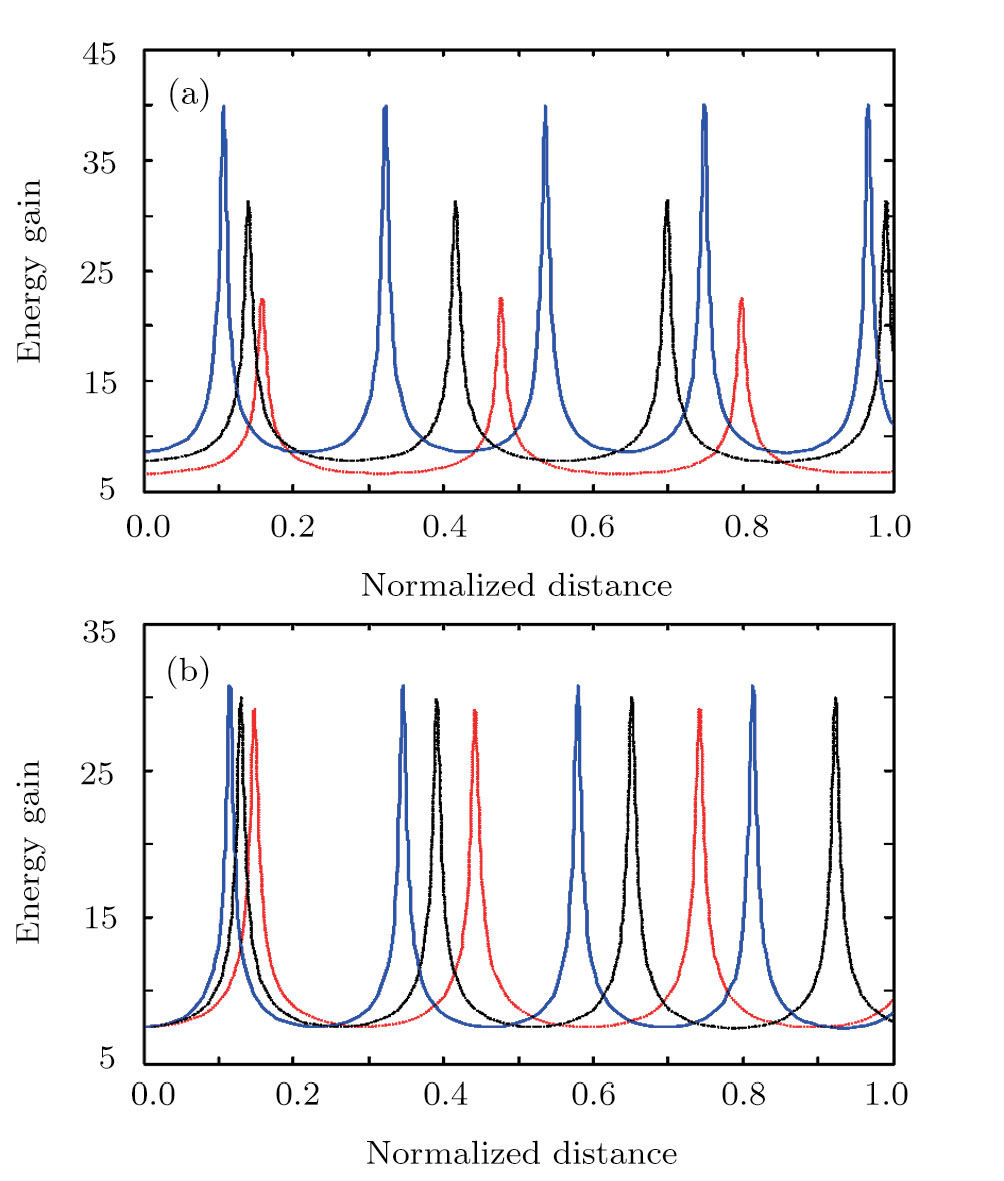
The large amplitude electron plasma wave can be used to accelerate the electrons in plasma beat wave accelerator scheme. Equation (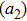
In conclusion, plasma wave generation and electron acceleration by beating of two intense HGBs in collisionless plasma with dominant relativistic-ponderomotive nonlinearity has been discussed. Paraxial-ray approximation has been used to establish the given formulation. Effects of laser and plasma parameters on the focusing of two HGBs in plasma at difference frequency, generation of electron plasma wave and particle acceleration process is examined. Following conclusions are made from the results:
(i) The order of the hollow Gaussian laser beams plays an important role in plasma beat wave accelerator scheme.
(ii) Focusing of both hollow Gaussian laser beams in plasma is enhanced by increasing the laser beam orders, incident laser intensity, and plasma density.
(iii) The intensity of both laser beams in plasma is higher for higher orders of the HGBs.
(iv) Maximum power of generated electron plasma wave depends on the extent of focusing of laser beams in plasma and the electric field associated with electron plasma wave respectively.
(v) The power of electron plasma wave increases by increasing the laser beam orders and the initial intensity of second/first laser beams.
(vi) The maximum energy gain also depends on the electric field associated with electron plasma wave and increases by increasing the laser beam orders and the initial intensity of second/first laser beams.
The results of the present investigation are relevant to laser beat wave based particle accelerators, terahertz generation and in other applications requiring multiple laser beams.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] |