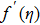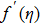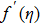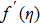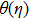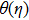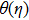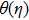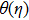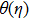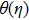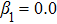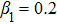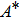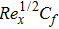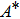† Corresponding author. E-mail:
Boundary layer stagnation point flow of Casson fluid over a Riga plate of variable thickness is investigated in present article. Riga plate is an electromagnetic actuator consists of enduring magnets and gyrated aligned array of alternating electrodes mounted on a plane surface. Physical problem is modeled and simplified under appropriate transformations. Effects of thermal radiation and viscous dissipation are incorporated. These differential equations are solved by Keller Box Scheme using MATLAB. Comparison is given with shooting techniques along with Range-Kutta Fehlberg method of order 5. Graphical and tabulated analysis is drawn. The results reveal that Eckert number, radiation and fluid parameters enhance temperature whereas they contribute in lowering rate of heat transfer. The numerical outcomes of present analysis depicts that Keller Box Method is capable and consistent to solve proposed nonlinear problem with high accuracy.
Radiation effects on flow and heat transfer is very important in the scaffold of space technology and processes involving high temperature. Visible light and infrared light emitted by an incandescent light bulb, the infrared radiation emitted by animals that is detectable with an infrared camera, and the cosmic microwave background radiation are some examples of thermal radiation. In manufacturing industries radiative heat transfer flow is very significant for depiction of reliable equipment, nuclear power plants, gas turbines and different propulsion devices for satellites, missiles, aircraft and space vehicles. Viscous and non-Newtonian fluids through various aspects and thermal radiation have been examined by many researchers. Pramanik[1] discussed numerical solutions for steady boundary layer flow and heat transfer for a Casson fluid over an exponentially permeable stretching surface in the presence of thermal radiation. He concluded that temperature as well as thermal boundary layer enhances due to thermal radiation. Hydromagnetic mixed convection heat and mass transfer flow of an incompressible Boussinesq fluid past a vertical porous plate with constant heat flux and thermal radiation is analyzed by Makinde.[2] The effects of thermal radiation over a stretching sheet under different flow geometries have been reported by several researchers.[3–5]
Impact of viscous dissipation is usually neglected but its presence become noteworthy when liquid viscosity is high. It changes the temperature distributions by playing a role like an energy source, which leads to affect heat transfer rates. Viscous dissipation is of interest for several applications such as notable temperature rises are witnessed in polymer processing, injection molding or extrusion at high rates. The effect of viscous dissipation was initially considered by Brickman.[6] According to him temperature distribution of Newtonian fluid in straight circular tube and interprets result that the effects were produced in the close region. Chand et al.[7] studied effects of viscous dissipation and radiation on unsteady flow of electrically conducting fluid through a porous stretching surface. He examined that Eckert number boost temperature profile. Hayat et al.[8] presented MHD stagnation point flow of Jeffrey fluid by a radially stretching surface with viscous dissipation and Joule heating. Hayat et al.,[9] Barik and Dash[10] also studied the flow of Newtonian fluid under the combined effects of thermal radiation and viscous dissipation. Some notable recent articles are cited in Refs. [11–19] and many therein. In nature, some non-Newtonian fluids behave like elastic solid that is, no flow occurs with small shear stress. Casson fluid is one of such fluids. The examples of Casson fluid are of the type as follows: jelly, tomato sauce, honey, soup and concentrated fruit juices. Human blood can also be treated as Casson fluid. In 1959, Casson introduced this fluid model for the prediction of flow behavior of pigment-oil suspensions.[20] Animasaun[21] has studied MHD dissipative Casson fluid flow with suction and n-th order of chemical reaction. He depicts that temperature and concentration are decreasing function of Casson fluid parameter. Nadeem et al.[22] put his contribution on Casson fluid past a linearly stretching sheet with convective boundary condition. Casson fluid model under different circumstances like thermal radiation, slip condition etc. is studied by many researchers (see Refs. [23–25]).
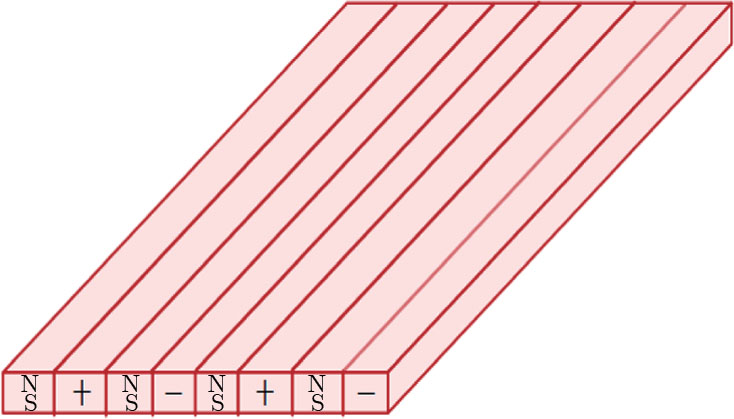
All of the above studies on Casson fluid had reported the boundary layer flow over stretching sheet in the absence of electrically conducting fluids over a Riga plate. This plate is used to produce magnetic field due to which Lorentz force is generated which controls the fluid flow. Riga plate is electromagnetic plate consisting of periodic pairs of electrodes proposed by Gailitis and Lielausis.[17] After identifying Lorentz force theoretically [26] and experimentally[27] as a resourceful mediator to reduce the skin friction; few recent studies of laminar fluid flow over a Riga plate has been reported. Pantokratoras and Magyari[28] explained EMHD free-convection boundary-layer flow from a Riga-plate. Later on, aiding and opposing mixed convection flows over the Riga-plate was investigated by Magyari and Pantokratoras.[29] Pantokratoras[30] considered Sakiadis and Blasius flow for Riga-plate by using finite difference method.
After reviewing above literature, it predicts that effect of viscous dissipation and thermal radiation for Casson fluid over an electrically conducted Riga plate incorporating with stagnation point has not been considered. Keeping this in mind, in present article we have studied the influences of viscous dissipation on boundary layer flow of a Casson fluid over a Riga plate in presence of activation energy near a stagnation point. Governing nonlinear ordinary differential equations are then solved by using finite difference approach named as Keller-Box scheme. To validate proposed scheme results comparison is provided with well establish, stable numerical procedure.
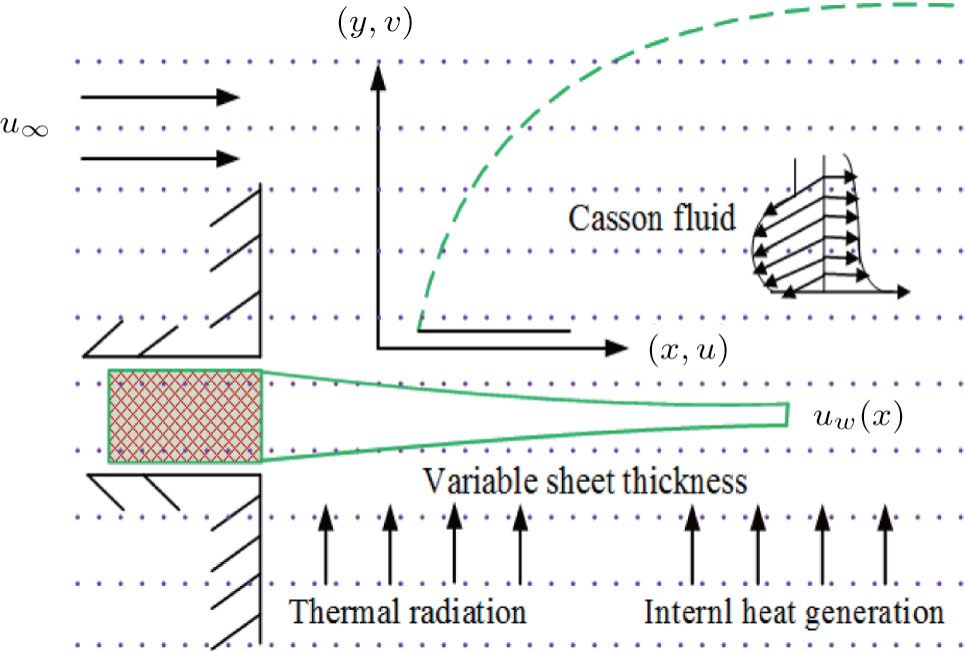
Present article focuses on study steady state, incompressible, two-dimensional flow of an electrically conducting Casson fluid over a stretchable Riga-plate. The plate is considered to have variable thickness δ, such that thickness is small relative to plate length. It is worth mentioning here that an alternate arry of electrodes and permanent magnets fixed on a plane surface constructs a Riga-plate (see Fig. 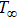
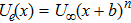
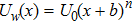
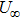
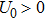
Now, governing boundary layer equations (see Refs. [23], [30], and [31]) of stagnation-point flow and heat transfer with internal heat generation of Casson fluid over Riga-plate are:

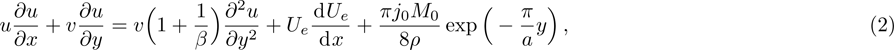
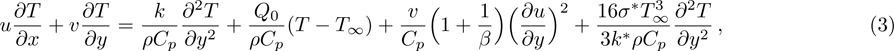
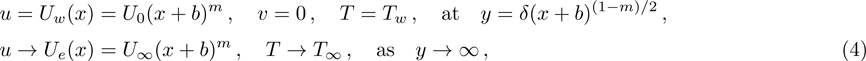
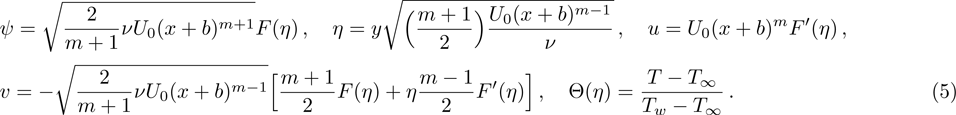
Equation (
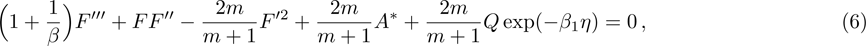
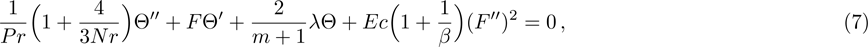
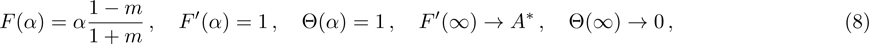
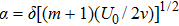
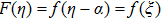
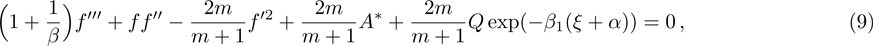
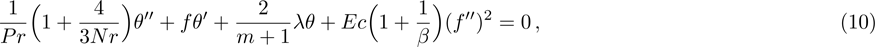
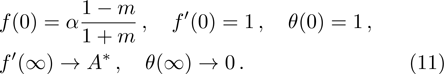
Furthermore, Prandtl number Pr, stretching rate ratio parameter 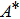
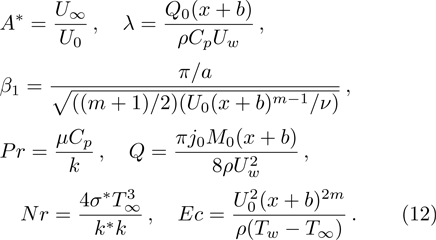
Significant physical quantities such as skin friction coefficient Cf and Nusselt number Nux are defined as
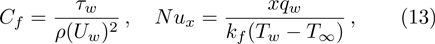
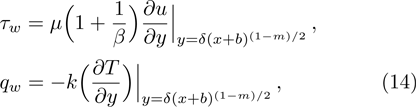
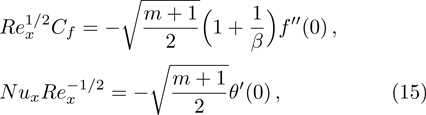
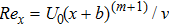
In order to solve nonlinear system (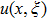
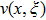
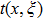
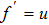
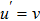
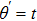
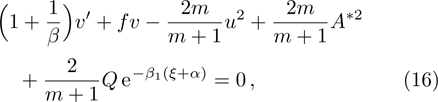
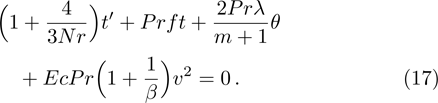
Moreover, domain discretize in x-η plane and according to mesh points, net points can be expressed as
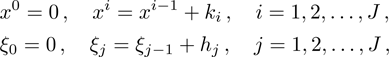
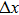
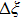
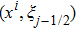
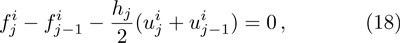
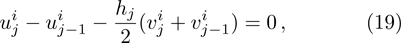
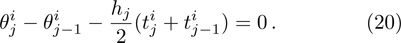
Central differencing of Eqs. (
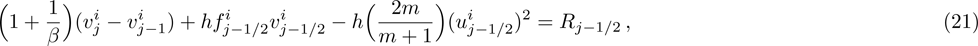
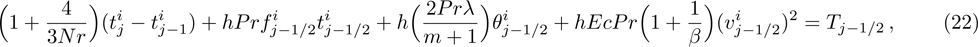
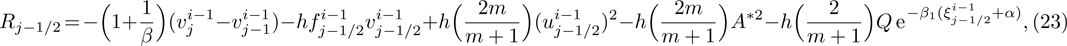
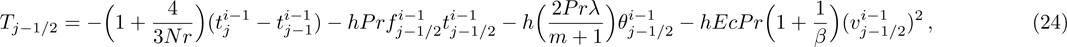
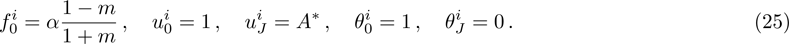
Linearization of Eqs. (
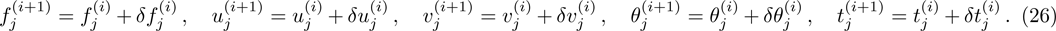
Incorporating above expressions in Eqs. (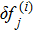
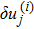
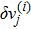
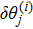
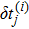
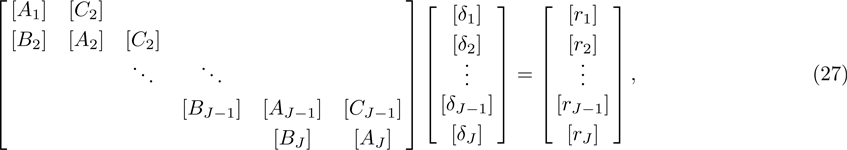
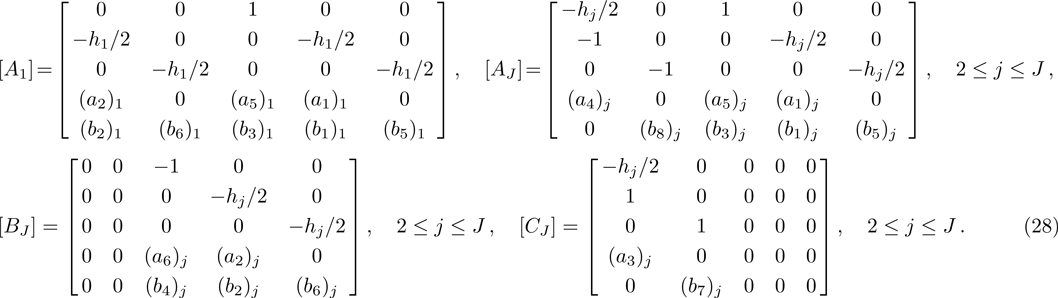
Block tri-diagonal matrix is solved by means of LU factorization. The value of δ is calculated repeatedly until

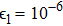
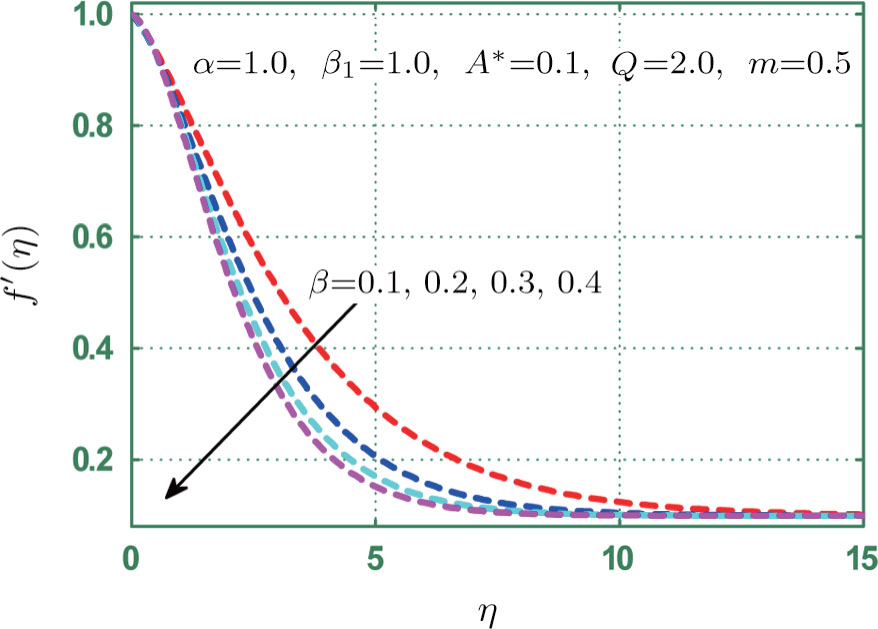
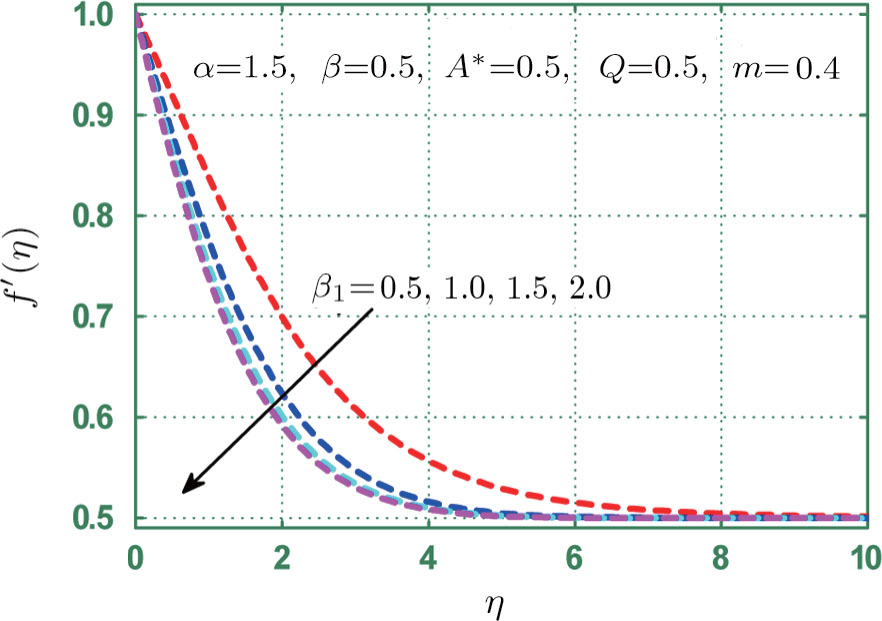
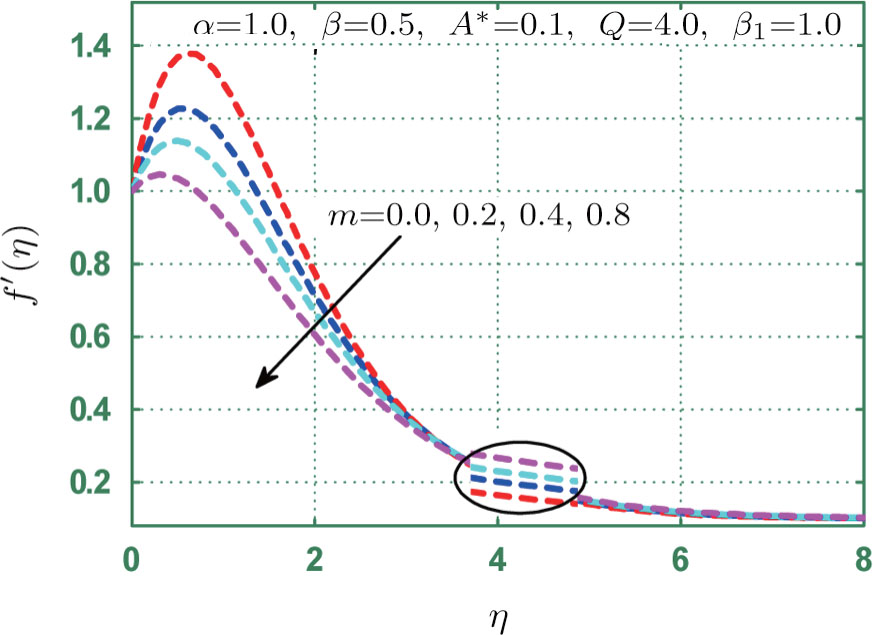
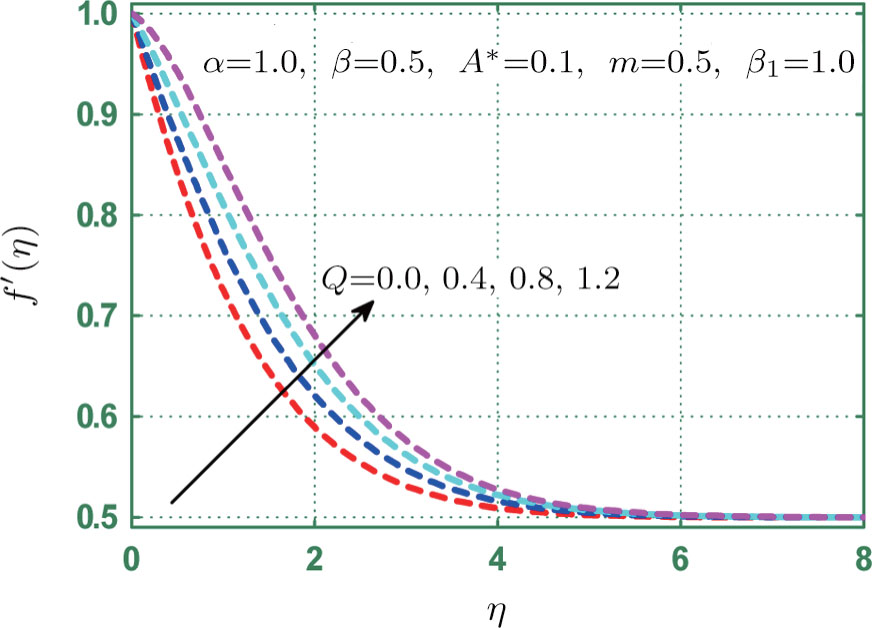
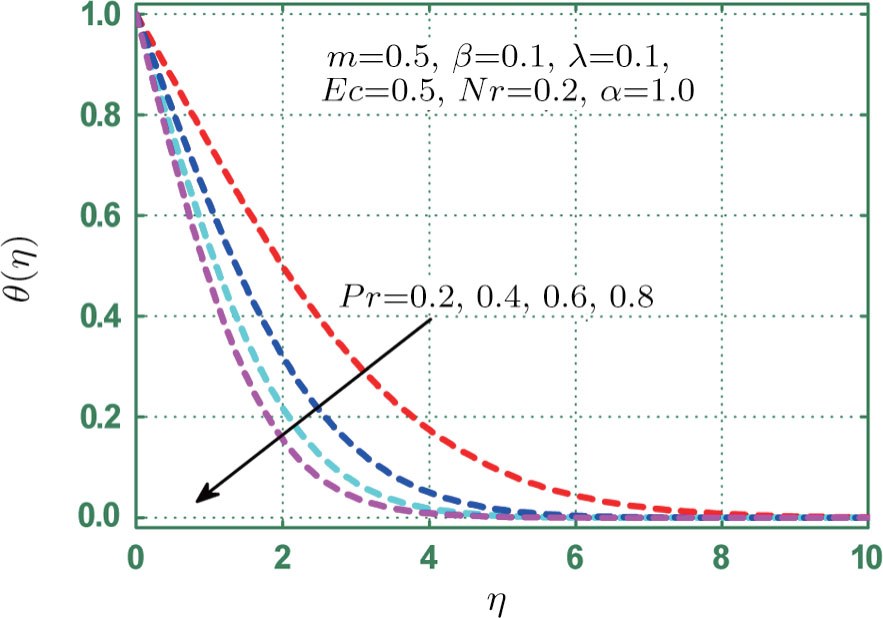
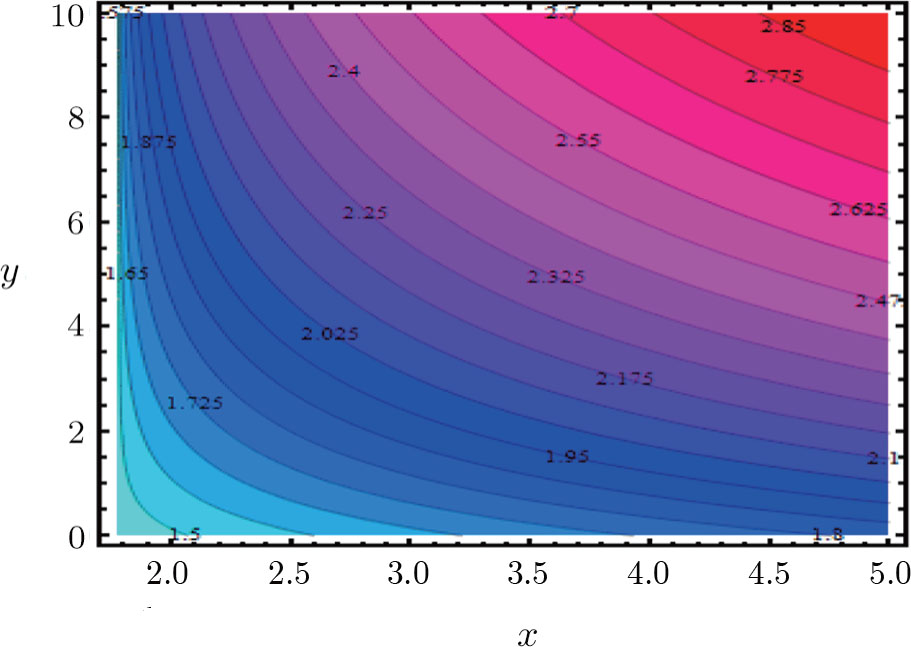
This section provides detailed study on graphical aspects of velocity 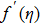
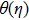
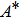
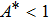
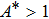
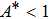
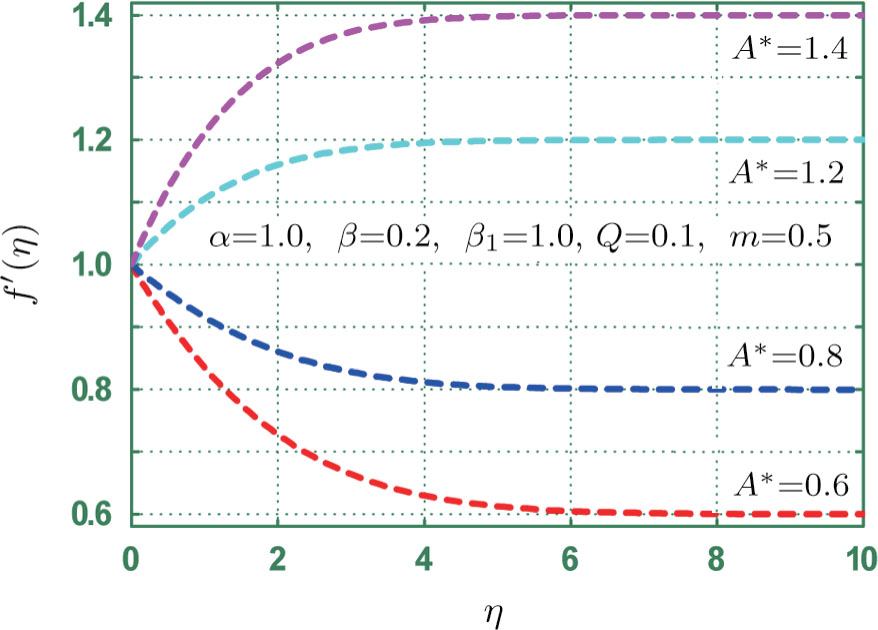
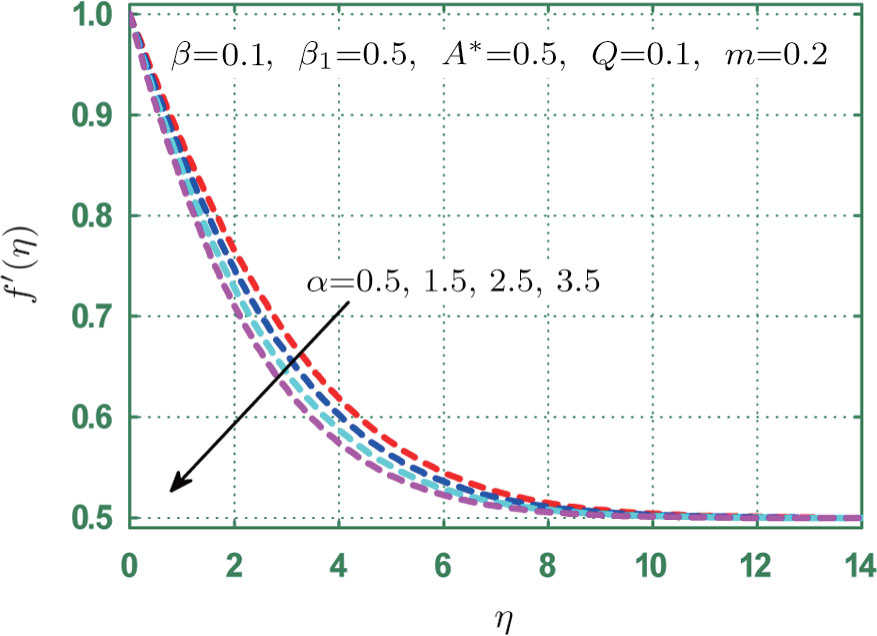
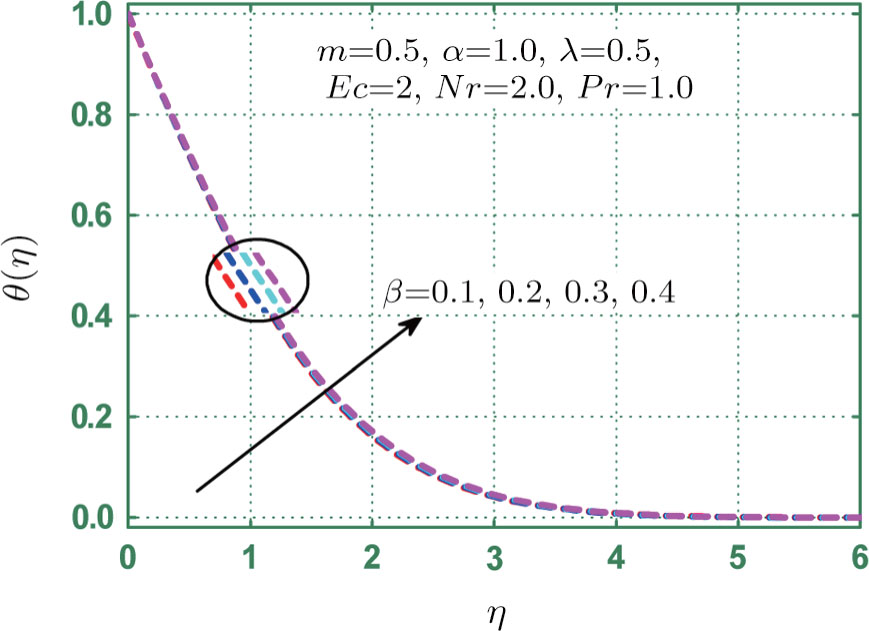
Figure 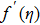
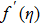
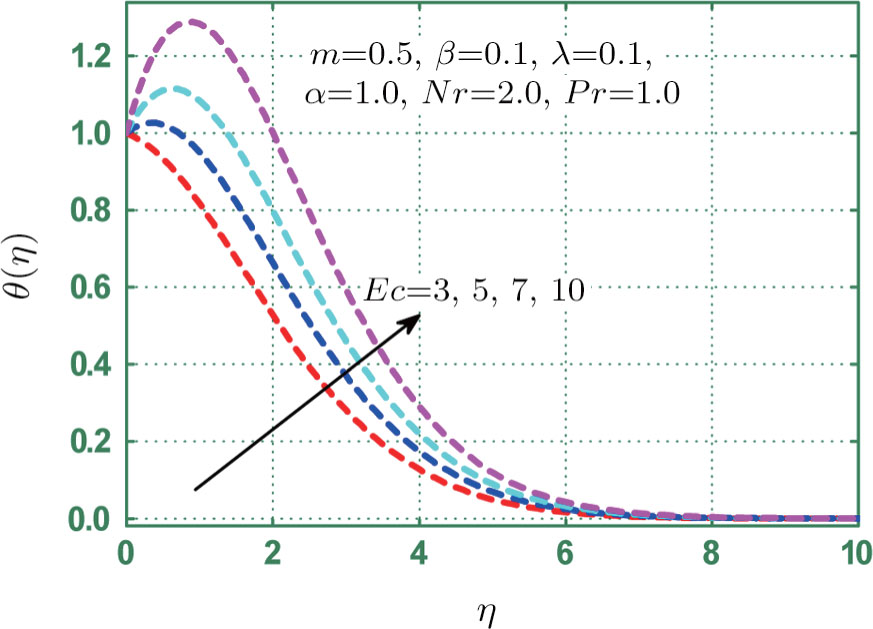
Physical analysis of velocity 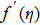
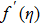
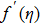
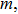
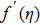
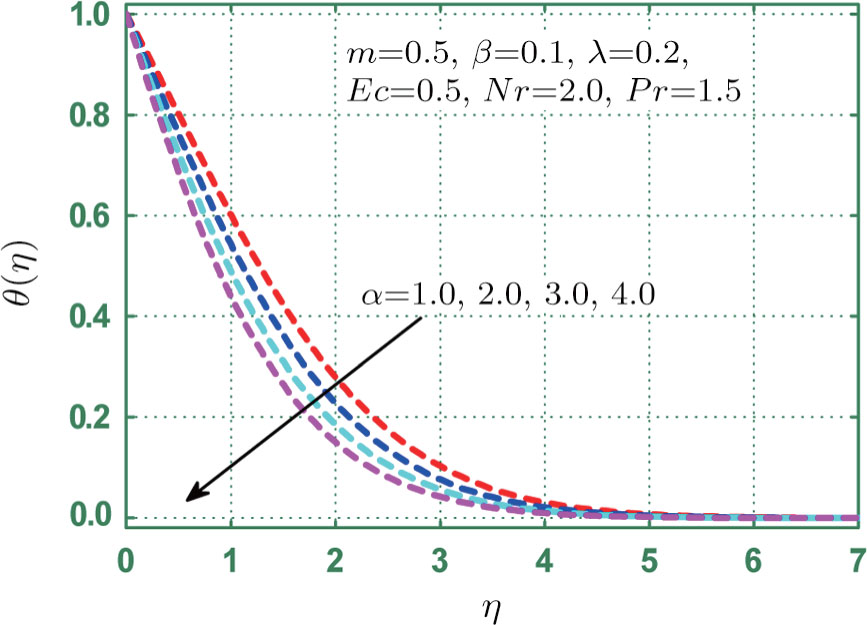
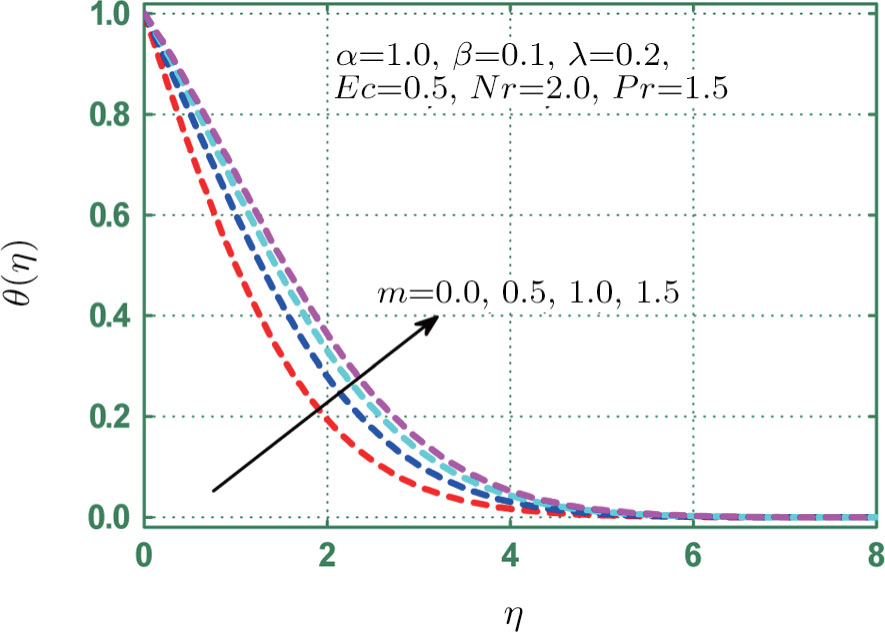
Figure 
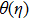
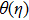
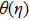
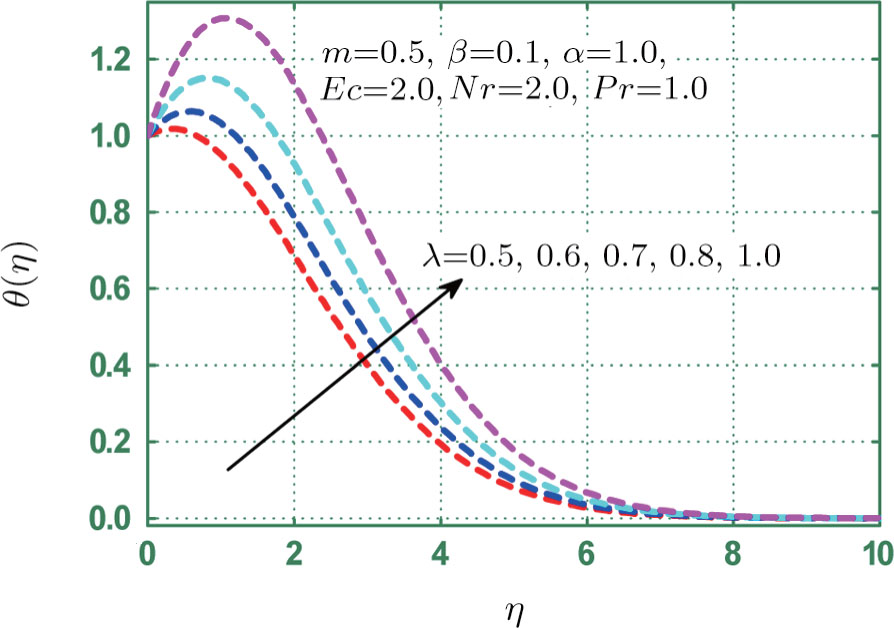
It results in increasing thermal energy of fluid, so temperature enhances with greater values of heat source parameter λ. This fact is analyzed through Fig. 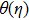
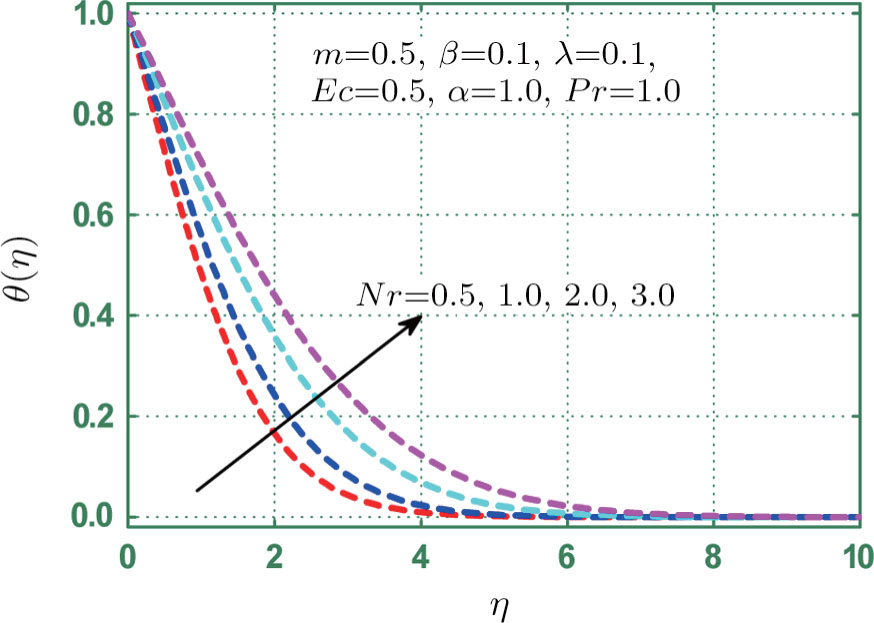
Radiation parameter amplifies fluid thermal capability. Hence temperature rises with thermal radiation parameter Nr as shown in Fig. 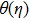
Further Table 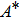
| Table 1
Tabulated skin friction values for distinct values of several parameters. . |
| Table 2
Numerical values of local heat flux for notable parameters. . |
Boundary layer stagnation point Casson flow problem influenced by thermal radiation and viscous dissipation is investigated over a Riga plate of variable thickness. Governing physical problem is tackled numerically using Keller Box Method. Moreover, a comparative numerical analysis is drawn with shooting method. This analysis will help in developing more understanding to boundary layer flow over an electromagnetic plate for viscoelastic fluids. Such type of problems are encounter in electronic and electric devices manufacturing. Graphical and numerical results are shown for various pertinent parameters on velocity and temperature distribution. It is concluded that velocity 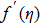
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] |