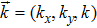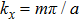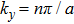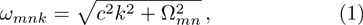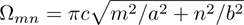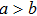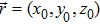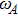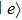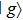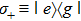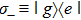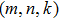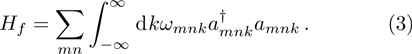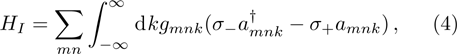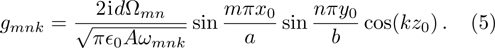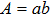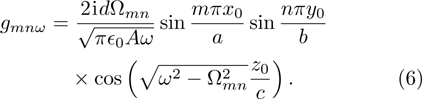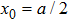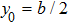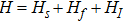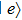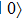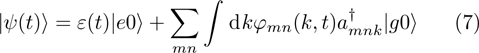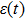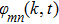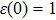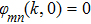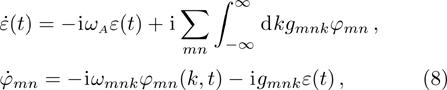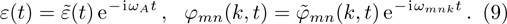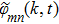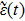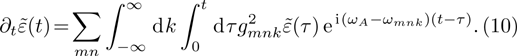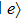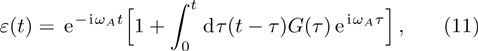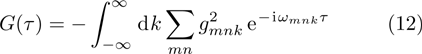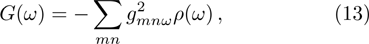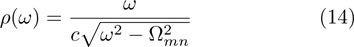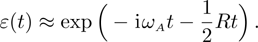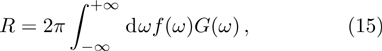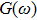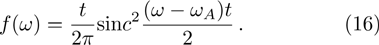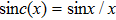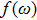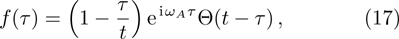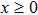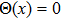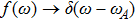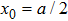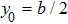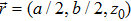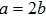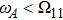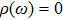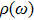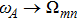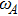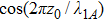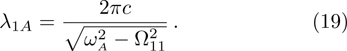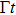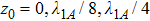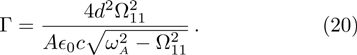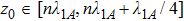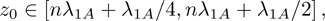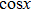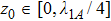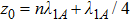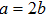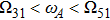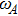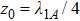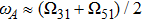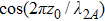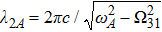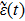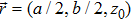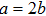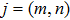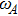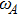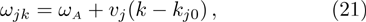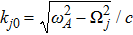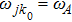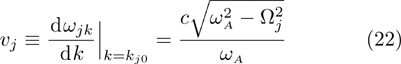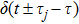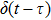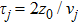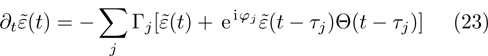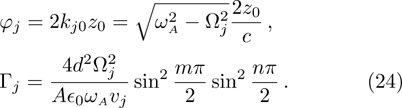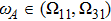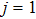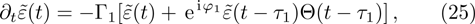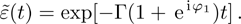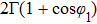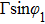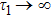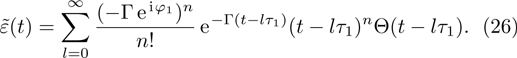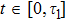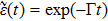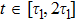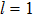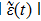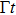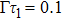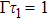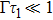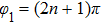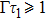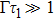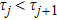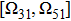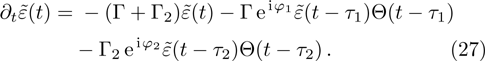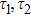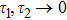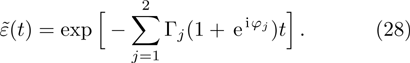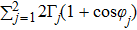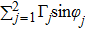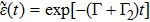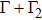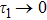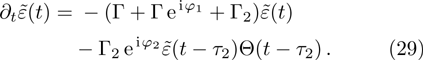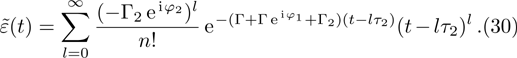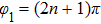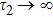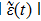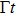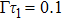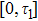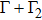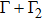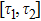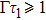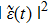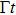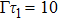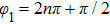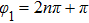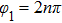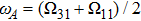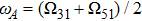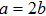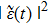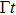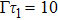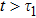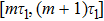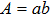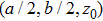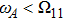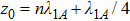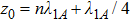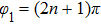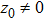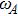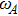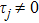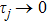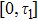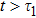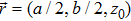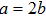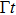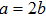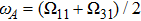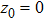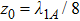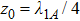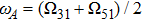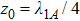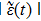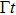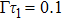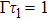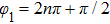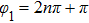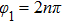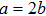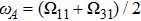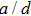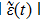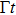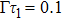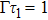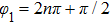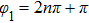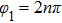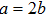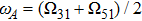Spatial Dependent Spontaneous Emission of an Atom in a Semi-Infinite Waveguide of Rectangular Cross Section
1 IntroductionAny quantum system inevitably interacts with its surroundings, which possess a huge amount of uncontrollable degrees of freedom. Such interaction causes the rapid destruction of quantum coherence, which is an essential requirement for quantum information processing to fully exploit the new possibilities opened by quantum mechanics. For example, the information stored in two-level systems (we refer to atoms hereafter) can be destroyed by their surrounding electromagnetic field. Spontaneous emission (SE) is one of the most prominent effects in the interaction of atoms with vacuum. It is an atomic radiation as follow: an atom is initially in an excited state relax to its ground state and emit a quanta of energy to its surrounding vacuum electromagnetic (EM) field, which carries away the difference in energy between the two levels.
SE is not only useless but also harmful to quantum information process. However, recently studies have shown that it is useful to build a device in a quantum network for controlling single photon by a local atom, e.g. the atomic radiation leads to the total reflection of the single-photon propagating in one quantum channel,[1–2] the frequency converter for single photon,[3] and the transfer of single photon from one quantum channel to the other.[4] Nowadays, great interest has been paid on the use of atoms to act as a quantum node in extended communication networks and scalable computational devices.[15–18] As the SE rate of a single atom can be modified by a succession of short and strong pulses or measure to the quantum system,[19–22] a dynamical Quantum-Zeno-Effect (QZE) switch for single photon is proposed.[5] The quantum interference between multiple transition pathways of atomic internal states has been exploited to modify the transport property of the single photon in a quantum channel.[9] With the well-known result that the atomic SE depends on the electromagnetic vacuum environment that the atom is subjected to, a boundary has been used to increase the efficiency of the quantum router.[12]
Actually, the SE rate of a single atom is one of the basic topic of quantum electrodynamics, numerous studies of the SE rates[23] have been carried out for atoms in free space (e.g. Ref. [24]), in a cavity (e.g. Ref. [25]), near a metallic mirror (e.g. Ref. [26]) or a dielectric interfacer (e.g. Ref. [27]), between two mirrors (e.g. Ref. [28]) or two dielectric interfaces (e.g. Ref. [29]). However, photons used to transmit information or distribute the entanglement along the network, are confined in a one-dimensional (1D) waveguide. Similar to cavities, 1D waveguide has a well-defined mode spectrum and a relatively loss-free environment. However, unlike cavities, modes are available in waveguide for photons to propagate. The geometry constraint not only confines the propagating direction of photon, but also gives rise to an increasing of the interference effects. Since photons do not interact with each other, atoms implanted in waveguide are necessary to mediate the photon-photon interaction or redirect the possible propagating directions. The coupling strength of atoms to the waveguide is enhanced by decreasing the mode volume. Consequently, the atomic radiation in 1D waveguide plays an important role in controlling photons in quantum networks. And the studies on the atoms in 1D waveguide are now referred to by the term “waveguide quantum electrodynamics (QED).”
Since the radiative properties of an atom in a confined space differ fundamentally from that in free space, considerable interest has been paid on atoms in a semi-infinite or infinite 1D waveguide. However most works focus on 1D waveguide without a cross section.[30–34] In this paper, we study the radiative properties of an atom in a semi-infinite waveguide of rectangular cross section, which is a typical 1D QED system. The termination of the waveguide is regarded as a perfect mirror, which reflects emitted photons back to the atom. We analyze the interaction of an initially excited two-level atom with the waveguide in vacuum. The Markovian approximation is first used to analyze the dependence of the SE rate on the density of states and the spatial profile of the waveguide. To find the influence of the time that one-photon wave packet requires to bounce back and forth between the atom and the mirror, we perform the linear expansion of the dispersion relation for the atomic transition frequency far away from the cutoff frequencies, and obtain a delay-differential equation. Then the atomic SE dynamics is studied by varying the cross section of the waveguide as well as the atomic location.
This paper is organized as follows. In Sec. 2, we introduce the system we have studied. In Sec. 3, we derive the relevant equations describing the dynamics of the system in single-excitation subspace. In Sec. 4, we do the Markovian approximation to study the effect of the mode profile on the spontaneous rate. In Sec. 5, the atomic dynamics is studied by linearly expanding the dispersion relation around the transition frequency, which is valid far from the branch threshold, where the delay time is introduced. Finally, we conclude this work in Sec. 6.
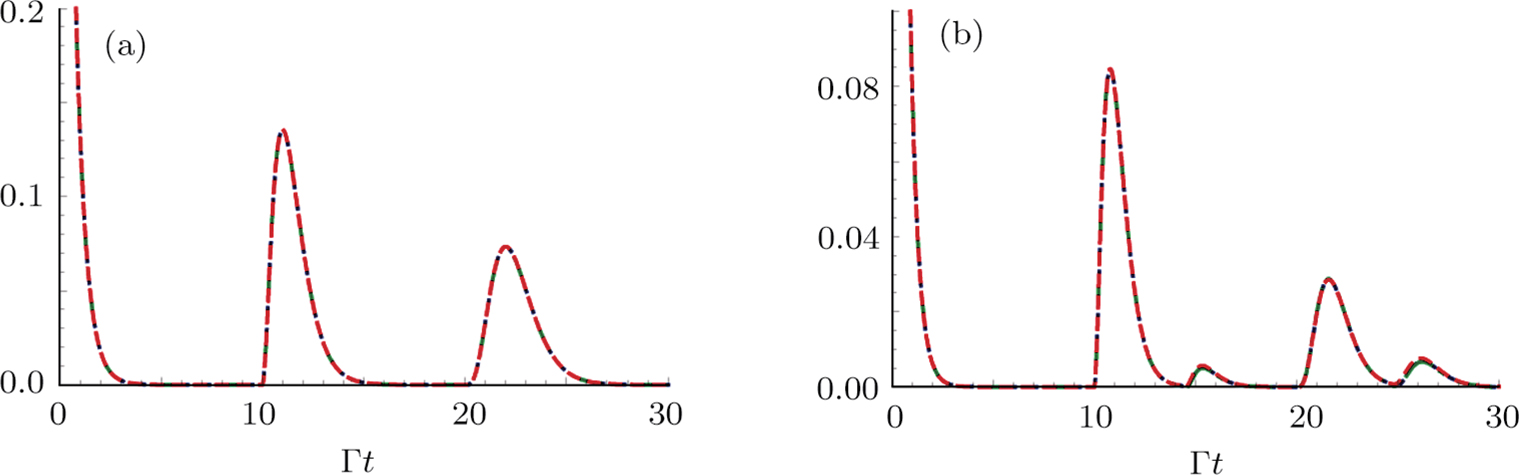
2 An Atom Inside a Rectangular Pipe WaveguideThe system we studied is shown in Fig. 1. A waveguide made of ideal perfect conducting walls is formed from surfaces at x = 0, x = a, y = 0, y = b, z = 0, and is placed along the z axis. The waveguide is assumed to be infinite along the z direction. The boundary condition restricts photons to travel without loss of power in two independent guiding modes:[35, 36] TE modes whose electric field has no longitudinal component, and TM modes whose magnetic field has no longitudinal component. Let 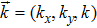 be the wave vector. The relations
be the wave vector. The relations 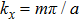 and
and 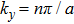 with positive integers n, m can be imposed by the condition that the tangential components of the electric field vanish at all the conducting wall, however, there is no constraint on k. Therefore, the waveguide allows a continuous range of frequencies described by the dispersion relation
with positive integers n, m can be imposed by the condition that the tangential components of the electric field vanish at all the conducting wall, however, there is no constraint on k. Therefore, the waveguide allows a continuous range of frequencies described by the dispersion relation
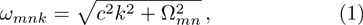
where
c is the speed of light in vacuum,
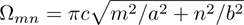
is the minimum frequency for a traveling wave. We note that
m and
n cannot both be zero. If
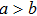
, TE
10 is the lowest guiding mode for the waveguide,
[37] and the lowest TM modes occur for
m = 1,
n = 1. Obviously, the waveguide modes form a one-dimensional continuum. Each guiding mode provides a quantum channel for photons to travel from one location to the other.
At 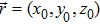 is an atom with transition frequency
is an atom with transition frequency 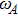 between upper level
between upper level 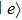 and lower level
and lower level 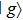 , which is excited initially. The atom sits inside the hollow waveguide. z0 is the distance between the atom to the wall (or the mirror) at z = 0. The free Hamiltonian for the atom is described by
, which is excited initially. The atom sits inside the hollow waveguide. z0 is the distance between the atom to the wall (or the mirror) at z = 0. The free Hamiltonian for the atom is described by

where
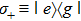
(
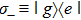
) is the rising (lowering) atomic operator. For the purpose of simplicity, the electric dipole of the stationary atom is assumed to be oriented along the
z direction, which means that the atom only interacts with the TM
mn modes. Since the number
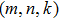
specifies the mode function of this air-filled metal pipe waveguide, we label the annihilation operator for each TM guiding mode by
amnk. The free Hamiltonian for the waveguide is described by
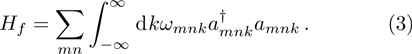
The interaction between the atom and field via the electric dipole coupling in the rotating-wave approximation reads
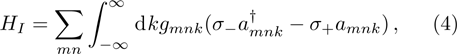
where the coupling strength
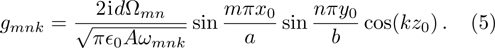
Here,
ϵ0 the permittivity of free space,
d the magnitude of the transition dipole moment of the atom and assumed to be real,
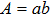
the area of the rectangular cross section. Using the dispersion relation, the coupling strength can be rewritten as
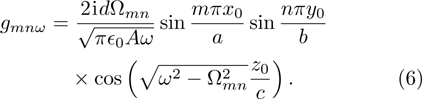
The cosine function in Eqs. (
5) and (
6) occurs due to the termination of the waveguide, which presents the difference from the infinite waveguide. Obviously, the atom located at
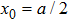
and
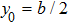
decouples to the TM
mn guiding mode with even integer
m or
n. The total system are described by Hamiltonian
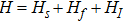
.
3 Evolution of the Atom-Vacuum SystemIn this section we study the dynamics of the system when the atom is initially in the excited state 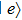 and the field is in the vacuum state
and the field is in the vacuum state 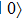 . Since the number of quanta is conserved in this system, we can write the wavefunction of the system as:
. Since the number of quanta is conserved in this system, we can write the wavefunction of the system as:
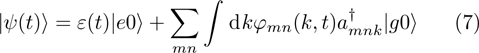
in one quantum subspace. The first term in Eq. (
7) describes the atom in the excited state with no photons in the field,
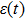
is the corresponding amplitude, whereas the second term in Eq. (
7) describes the atom in the ground state with a photon emitted at a mode
k of the TM
mn guiding mode,
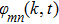
is the corresponding amplitude. The initial state of the system is denoted by the amplitudes
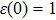
,
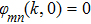
. The Schrödinger equation results in the following coupled equation of the amplitudes
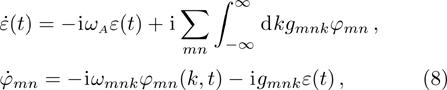
where the overdot indicates the derivative with respect to time. The population of the atomic excited state are usually analyzed by eliminating the field variables and focusing on the dynamics of the radiating system. We start by removing the high frequency term in Eq. (
8) via the transformation
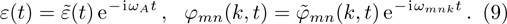
Then we formally integrate equation of
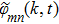
, which is later inserted into the equation for
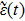
. The probability amplitude for the excited atomic state is determined by the following integro-differential equation
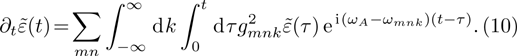
Equation (
10) shows that the value of
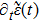
depends on the values of
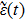
at all earlier time.
4 Spatial Dependence of the Spontaneous RateTo see how the mode distribution of the quantum vacuum fluctuation modifies the atomic spontaneous rate, we set 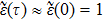 on the right-hand side of Eq. (10), and the amplitude of level
on the right-hand side of Eq. (10), and the amplitude of level 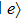 reads
reads
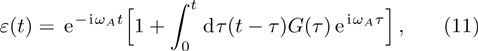
where the reservoir response (memory) function
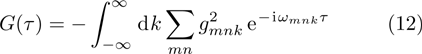
characterizes the spectrum of the rectangular hollow waveguide. Its Fourier transformation yields the coupling spectrum
[38, 39]
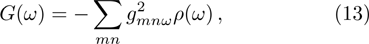
which is the density of states
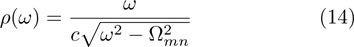
weighted by the strength of the coupling to the continuum. Since the dispersion relation of the semi-infinite waveguide is the same as that of the infinite rectangular waveguide,
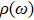
in Eq. (
14) is also the density of state of the infinite rectangular waveguide. For weak atom-field coupling, the amplitude of level
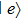
decays exponentially
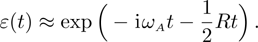
Accordingly, the SE rate, the key ingredient in the SE dynamics, reads
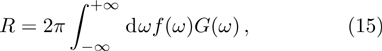
which is the overlap of the coupling spectrum
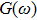
and the modulation spectrum
[38, 39]
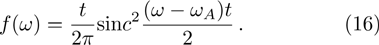
Here,
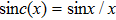
. the modulation spectrum is symmetrically centered on
ωa and decays in amplitude as
t−1. Function
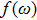
is the Fourier transform of the function
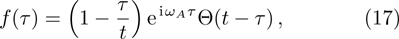
where
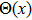
is the Heaviside unit step function, i.e.,
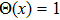
for
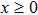
, and
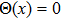
for
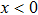
. Taking the limit
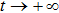
, the modulation spectrum
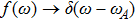
, then we obtain the golden rule value

The modal profile affects on the decay rate via location of the atom. If the atom is located at
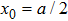
and
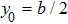
, no photons are radiated into the TM
mn guiding mode with even integer
m or
n since the guiding mode is standing waves in the transverse direction. The cutoff frequencies also affect the decay rate via the local density of states. In Fig.
1(b), we have given a schematic diagram of the dispersion relation of the guiding modes, which interact with the atom at
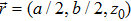
for
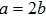
. If the transition frequency
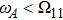
, SE cannot occur since
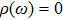
. Since
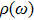
tends to infinite when
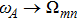
, the excited state population decays very rapidly. When
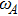
is located in the frequency band between Ω
11 and Ω
31, the TM
11 guiding mode contributes to the spontaneous rate. However, there is an enhancement or inhibition of spontaneous decay depending on the factor
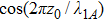
, where the wave length
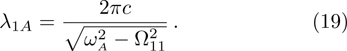
In Fig.
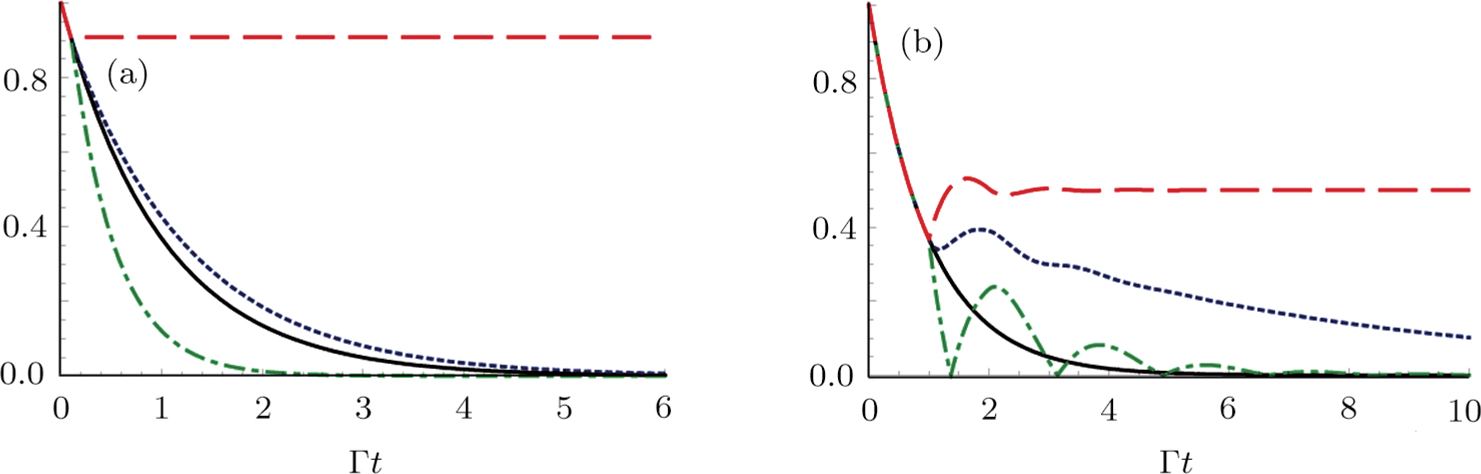
2(a), we have plotted the probability of finding the atom in its excited state as a function of
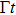
for three different values of
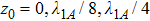
, where
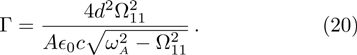
It can be seen that in the interval
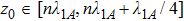
with integer
n, the SE rate decreases as the atom-mirror separation increases. However in the interval
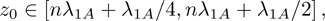
its SE rate increases as
z0 increases. Since
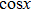
is a periodical function of the argument
x, the figure is only plotted in
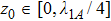
. It can be seen that at
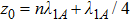
, the SE is completely suppressed. Since we have set that
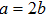
, TM
51 and TM
13 is the third and fourth guiding modes, which might be interacting with the atom. When
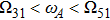
, the atom interacts with the continua of two guiding modes TM
11 and TM
31. The spontaneous rate increases although it still depends on
z0. As
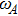
increases, more and more guiding modes are included to increase the spontaneous rate. In Fig.
2(b), we have plotted the atomic excitation probability with
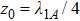
and
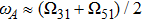
. In this case, the TM
11 mode does not contribute to the SE (see the red dashed line), however, the SE is still enhanced, this enhancement is due to the atomic coupling to the continuum of TM
31 mode (see the blue solid line). One can understand this from Eq. (
18) that the SE rate of the atom caused by the TM
31 mode is also dependent of the factor
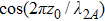
, where
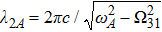
. Since the wavelength of the radiation emitted by the atom into the continuum is different for different guiding modes, the SE is generally increased when more guiding modes interact with the atom.
One can also obtain the spontaneous rate in Eq. (18) by replacing  with
with 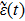 in Eq. (10) and making the up limit of integral tend to infinite. Hence, the Markovian approximation yields the same phenomenon in the context below Eq. (18), which means that retardation effect is neglected.
in Eq. (10) and making the up limit of integral tend to infinite. Hence, the Markovian approximation yields the same phenomenon in the context below Eq. (18), which means that retardation effect is neglected.
5 Atomic Population of the Excited StateAn excited atom relaxes to its ground state accompanied by a release of a photon to the EM vacuum. In this hollow waveguide, the emitted photon propagates along the positive and negative z directions. Since the termination of the waveguide imposes a hard-wall boundary condition on the field, which behaves as a perfect mirror, the photon traveling along the negative z axis is retroreflected to the atom, and re-excites the atom, which leads to a non-Markovian type dynamics of the system.[40] In this section, we study the spontaneous emission dynamics involving the retardation time for atom located at 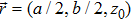 with
with 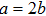 . For the convenience of discussion, we denote the transversally confined propagating modes, which couple to the atom as TMj with
. For the convenience of discussion, we denote the transversally confined propagating modes, which couple to the atom as TMj with 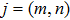 according to the ascending order of the cutoff frequencies. By assuming that the transition frequency
according to the ascending order of the cutoff frequencies. By assuming that the transition frequency 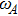 is far away from the cutoff frequencies Ωj, we can expand frequency ωjk around the transition frequency
is far away from the cutoff frequencies Ωj, we can expand frequency ωjk around the transition frequency 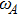 up to the linear term
up to the linear term
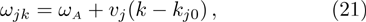
where
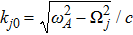
is determined by
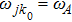
and the group velocity
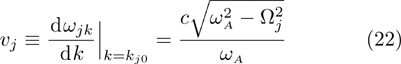
is different for different TM
j guiding modes. We substitute Eq. (
21) into integro-differential Eq. (
10). Integrating over all wave vectors
k gives rise to a linear combination of
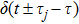
and
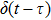
, where
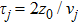
is the time that the emitted photon take the round trip between the atom and the mirror in the give transverse mode
j. We approximately obtain a delay-differential equation
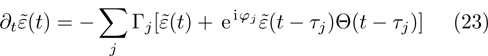
for the probability amplitude that the atom at time
t is in the excited state, where
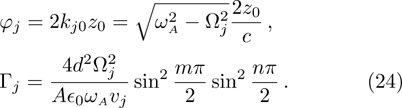
The first term on the right hand side of Eq. (
23) leads to the exponential decay of the atom. The second term involved the time
τj that the light needs for the distance atom-mirror-atom, which represents the effect of the reflected radiation on the atom that was emitted at time
τj in the TM
mn mode before it interacts again with the atom.
5.1 SE Dynamics in Single ModeIn the frequency band between Ω11 and Ω31, the waveguide is said to be single-moded. The atom with the transition frequency 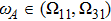 only interacts with the TM11 (
only interacts with the TM11 (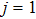 ) guiding mode, the delay-differential equation reduces to
) guiding mode, the delay-differential equation reduces to
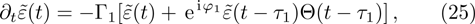
where
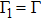
given in Eq. (
20). For the case that the retarded argument
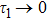
, the memory effects inherent in the system disappear. The amplitude of state
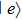
becomes
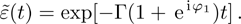
The SE rate and the frequency shift are presented by the real part
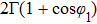
and imagine part
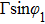
, respectively. In the limit
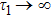
, the second term of Eq. (
25) vanishes. Since the waveguide becomes infinite, the atomic population decays exponentially and the SE rate Γ is independent of the coordinate
z0.
It can be seen from Eq. (25) that the time axis is divided into intervals of length τ1. We can formally integrate Eq. (25) and change the dummy integration variable, which is then substituted into the integrand. Proceeding indefinitely with iteration, the time behavior of the atomic state populations reads
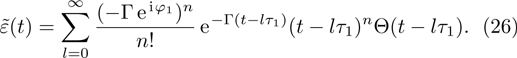
A step character is presented in Eq. (
26). For
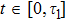
, the atomic amplitude
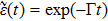
decays exponentially, which coincides with the behavior of an excited atom in an infinite waveguide. The underlying physics is that the atom requires at least the time
τ1 to recognize the mirror. For
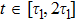
, due to the emitted radiation reflected back to the atom,
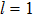
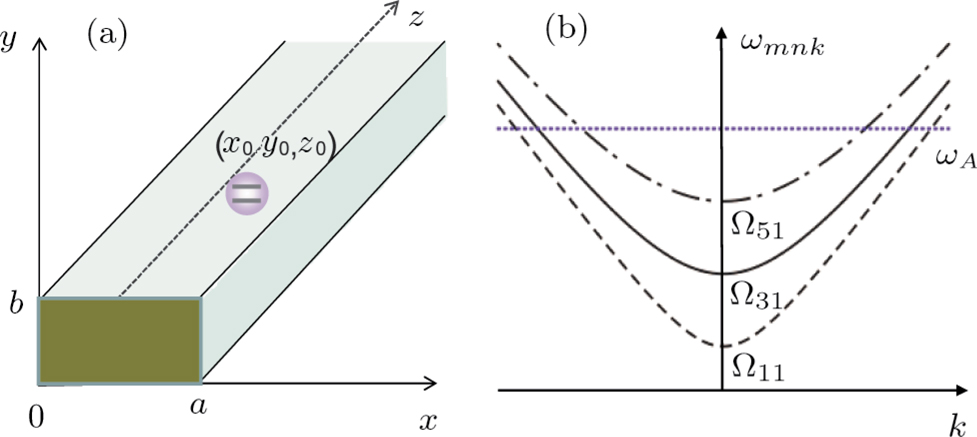
term has been included, which gives rise to the interference for finding the atom in the excited state. In Fig.
3, we have plotted the norm
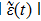
of the atomic amplitude versus
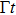
with delay
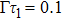
(a) and
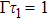
(b). The exponential decay of the atom inside an infinite waveguide is plotted with the black solid line. When
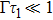
, an exponential decay law is found, however, the SE can be either increased or descreased by the phase. The SE is completely suppressed when phase
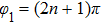
. When
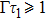
, the atom first decays exponentially, after the atom recognizes the mirror, it displays a behavior deviating from the exponential decay law, and a partial revival of the atomic population can be found. It is the interference between the emitted wave and the radiation wave reflected back to the atom, which makes the atom-mirror separation
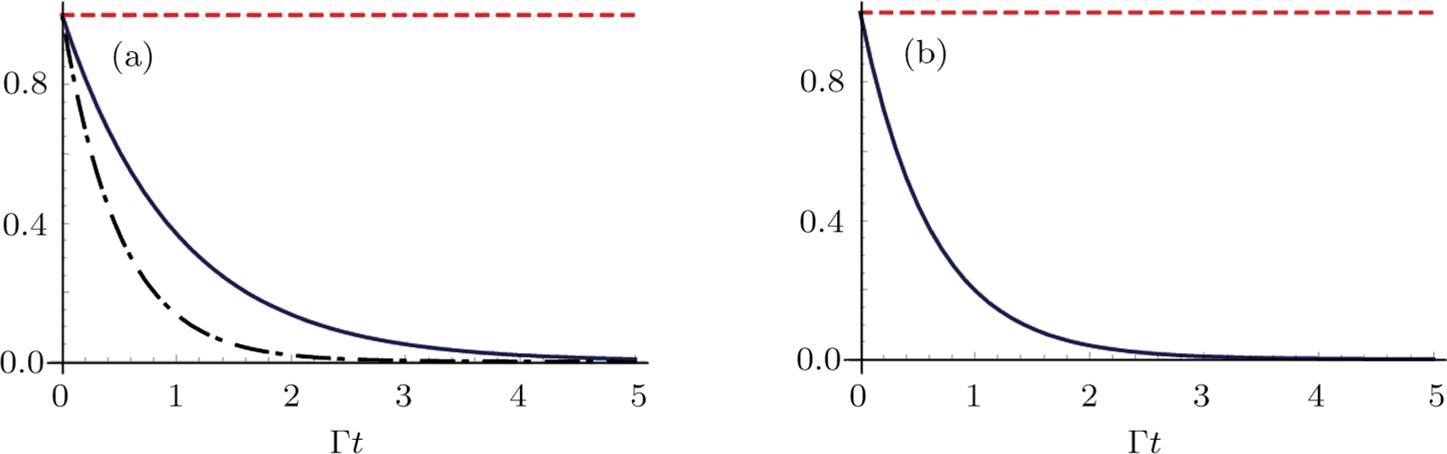
z0 has significant influence on the atomic dynamic via the phase. When the distance between the atom and the termination are further large (i.e.,
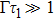
), it is found from Fig.
5(a) that there is also a partial revival of the atomic population, however, the atom-mirror separation
z0 does not make any sense. In this case, the atom has already decayed to the ground state at the time that the photon bounces back to the atom, so there is no emitted wave to be interference with the wave reflected back to the atom, which means that the atomic revival is due to the atom being partially re-excited by the radiation. Since the light emitted in the positive direction has departed from the atom, the probability that the atom is re-excited becomes lower and lower.
5.2 SE Dynamics in Multiple ModesAn excited atom radiates waves into the continua of all modes resonant with the atom. When the cross area becomes larger, more modes are included in the resonance, then the atomic dynamics is not only affected by the time τ1 that light needs to bounce back and forth between the atom and the termination in the TM11 mode, but also by other time τj required for a photon emitted by the atom to propagate in the TMmn mode and reabsorbed by the atom. The definition of delay time τj told us that 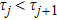 .
.
In this section, we assume that the atomic transition frequency is in the regime 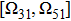 , which means that only two TM modes (i.e. TM11, TM31) in resonance with the atom, the delay-differential equation reduces to
, which means that only two TM modes (i.e. TM11, TM31) in resonance with the atom, the delay-differential equation reduces to
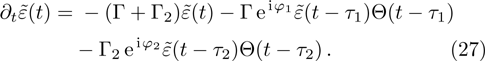
The space dependence enters via both the phases
φ1,
φ2 and the delay time
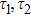
of the different modes. If both arguments
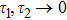
, the amplitude of state
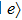
becomes
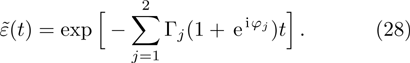
Two terms are consisted of in the above equation, the SE rate
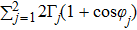
and frequency shift
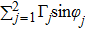
. Comparing to the single mode case, the SE rate is enhanced, however the frequency shift can be either increased or decreased due to the space dependence. In the limit
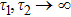
, the second and third terms of Eq. (
27) vanish. The amplitude
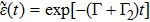
shows that the atomic population decays exponentially,
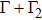
is the SE rate that the atom interacts with the continuum of the TM
11 and TM
31 modes of an infinite waveguide, which is also independent of the coordinate
z0. In the case that
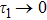
, the delay-differential equation reads
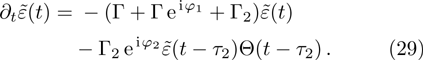
Using Laplace transformation and geometric series expansion, the solution reads
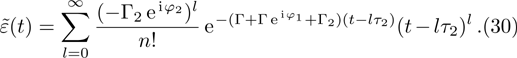
If the atom is located at
z0 satisfying
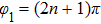
, the SE that the TM
11 mode contributes to is completely suppressed, then one obtains the SE dynamics due to the emitted photon propagating only via the continuum of the TM
31 mode. In the case with finite
τ1 and
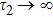
, the upper state amplitude becomes
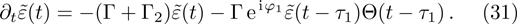
However, it is impossible for an atom inside a realistic waveguide to appear the dynamics described by Eq. (
31).
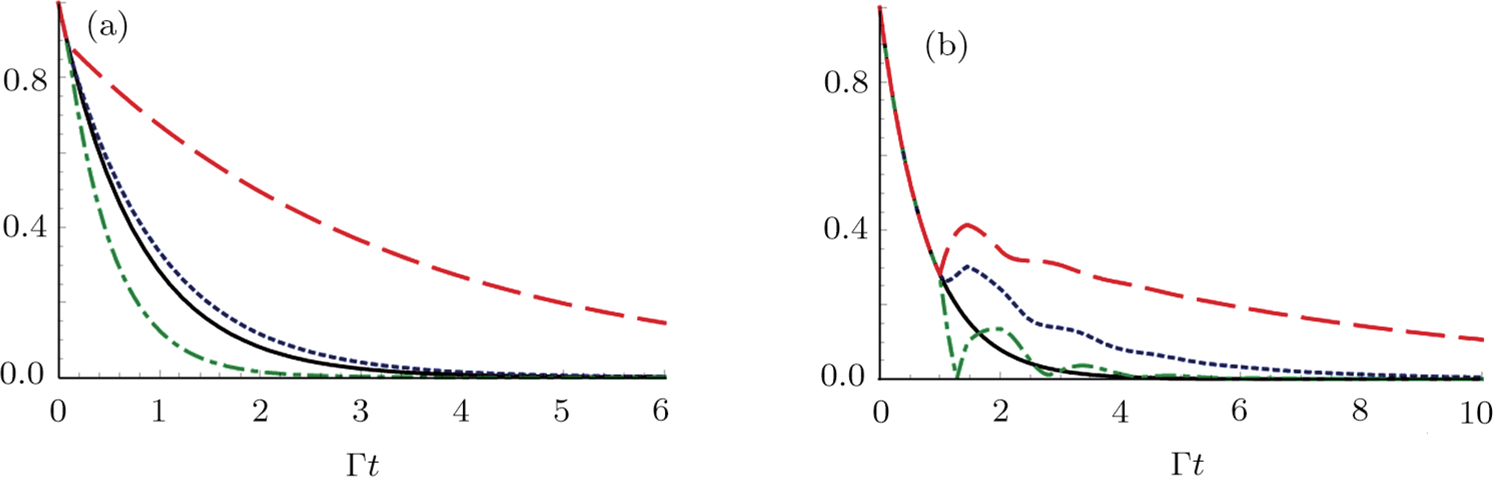
In Fig. 4, we have numerically plotted the amplitude 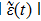 as a function of
as a function of 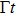 with
with 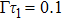 (a) and 1 (b). It can be seen that in the interval
(a) and 1 (b). It can be seen that in the interval 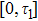 , the upper state population of the atom decays exponential with a rate
, the upper state population of the atom decays exponential with a rate 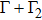 . After time τ1, photons emitted by the atom are reflected back to the atom by the mirror so that the atom-mirror distance has great influence on the SE dynamics via phase φj and τj. Phase φ1 first gives arise to deviation from the decay with a rate
. After time τ1, photons emitted by the atom are reflected back to the atom by the mirror so that the atom-mirror distance has great influence on the SE dynamics via phase φj and τj. Phase φ1 first gives arise to deviation from the decay with a rate 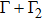 in the interval
in the interval 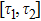 . As soon as
. As soon as 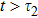 , the wave propagating in the TM31 mode is reflected back to the atom by the mirror, phase φ2 deviates the atomic dynamics from that of finite τ1 and
, the wave propagating in the TM31 mode is reflected back to the atom by the mirror, phase φ2 deviates the atomic dynamics from that of finite τ1 and 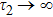 . In the weak coupling case (see, Fig. 4(a), the excited state probability decreases as the time increases. However, in the strong coupling case, several peaks can be observed in Fig. 4(b), which present partial revivals of the atom probability when
. In the weak coupling case (see, Fig. 4(a), the excited state probability decreases as the time increases. However, in the strong coupling case, several peaks can be observed in Fig. 4(b), which present partial revivals of the atom probability when 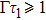 . Comparing to the time evolution in Fig. 3, the SE is enhanced for a given phase φ1. Phase φ2 and retardation time τ2 shift the position of the peak and the dip.
. Comparing to the time evolution in Fig. 3, the SE is enhanced for a given phase φ1. Phase φ2 and retardation time τ2 shift the position of the peak and the dip.
In Fig. 5, we have numerically plotted the probability 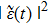 as a function of
as a function of 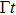 with delay
with delay 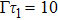 for (a) single-moded and (b) double-moded cases. When the photon returns back to the atom, the atom has already decayed to its ground state, it is impossible for interference to occur so that the phases φj have no effect on the atomic dynamics. The peaks at time
for (a) single-moded and (b) double-moded cases. When the photon returns back to the atom, the atom has already decayed to its ground state, it is impossible for interference to occur so that the phases φj have no effect on the atomic dynamics. The peaks at time 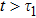 owe to the reflected light reabsorbed by the atom. By comparing two figures in Fig. 5, we found that the probability that the atom is reexcited by the radiation wave is lower in the multiple-mode case than that in the single-mode case, and more peaks appear in the interval
owe to the reflected light reabsorbed by the atom. By comparing two figures in Fig. 5, we found that the probability that the atom is reexcited by the radiation wave is lower in the multiple-mode case than that in the single-mode case, and more peaks appear in the interval 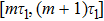 for the multiple-mode case. Such observations are easy to understand because there are more transverse modes to interact with the atom.
for the multiple-mode case. Such observations are easy to understand because there are more transverse modes to interact with the atom.
6 Discussion and ConclusionWe have studed the dynamics of an atom inside a hollow waveguide of rectangular cross section 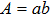 , made of ideal perfect conducting walls. Such 1D waveguide generally consists of both TE and TM waves, the atom with dipole along the z-direction interacts only with the TMmn transverse modes, their coupling strength depends on the atomic location. A two-level atom with location fixed at
, made of ideal perfect conducting walls. Such 1D waveguide generally consists of both TE and TM waves, the atom with dipole along the z-direction interacts only with the TMmn transverse modes, their coupling strength depends on the atomic location. A two-level atom with location fixed at 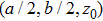 is considered, which decouples to fields of the TM modes with even integer m, n. We have first discussed the dependence of the SE rate on the atom-mirror separation and the density of states by Markovian approximation (i) Since the density of state vanishes below Ω11, the SE is completely suppressed when
is considered, which decouples to fields of the TM modes with even integer m, n. We have first discussed the dependence of the SE rate on the atom-mirror separation and the density of states by Markovian approximation (i) Since the density of state vanishes below Ω11, the SE is completely suppressed when 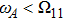 ; (ii) Since the density of state tends to infinite, the excited state population decays very rapidly when
; (ii) Since the density of state tends to infinite, the excited state population decays very rapidly when 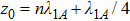 , (iii) Away from the cutoff frequencies, the SE rate is increased when more TM modes in resonance with the atom, and the upper state population could be unchanged all the time for single mode case with
, (iii) Away from the cutoff frequencies, the SE rate is increased when more TM modes in resonance with the atom, and the upper state population could be unchanged all the time for single mode case with 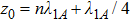 (i.e.,
(i.e., 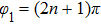 ). However, the distance
). However, the distance 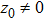 gives rise to the time delay that radiation emitted by the atom return to the emitter. To study this backaction of the ideal perfect conducting at
gives rise to the time delay that radiation emitted by the atom return to the emitter. To study this backaction of the ideal perfect conducting at 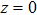 on the atom, we perform a linear approximation, which is valid for
on the atom, we perform a linear approximation, which is valid for 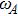 far from the cutoff frequencies, and phase φj and retardation time τj are introduced into the dynamics of the atom via
far from the cutoff frequencies, and phase φj and retardation time τj are introduced into the dynamics of the atom via 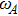 and z0. The SE dynamics is studied for both single-moded and double-moded cases. We find that (i) the upper state population is less than its initial as long as
and z0. The SE dynamics is studied for both single-moded and double-moded cases. We find that (i) the upper state population is less than its initial as long as 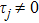 . The discussion in Markov approximation corresponds to the case with the retardation time
. The discussion in Markov approximation corresponds to the case with the retardation time 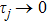 . (ii) The probability for finding the atom in its excited state is lowered when more transverse modes are resonant with the atom. (iii) In the interval
. (ii) The probability for finding the atom in its excited state is lowered when more transverse modes are resonant with the atom. (iii) In the interval 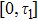 , the atomic behavior is the same to that of an excited atom in an infinite waveguide, and the SE rate is independent of z0. (iv) After
, the atomic behavior is the same to that of an excited atom in an infinite waveguide, and the SE rate is independent of z0. (iv) After 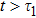 , two situations should be distinguished. For short retardation time, the interference between the radiation wave and the emitted wave makes the dynamics is strongly dependent on φj. For long retardation time, the atom has already decay to its ground state when the photon returns back to the atom, the partial revivals and collapses are due to the photon reabsorbed and re-emitted by the atom.
, two situations should be distinguished. For short retardation time, the interference between the radiation wave and the emitted wave makes the dynamics is strongly dependent on φj. For long retardation time, the atom has already decay to its ground state when the photon returns back to the atom, the partial revivals and collapses are due to the photon reabsorbed and re-emitted by the atom.