† Corresponding author. E-mail:
The generalized fractional Burgers equation is studied in this paper. Using the classical Lie symmetry method, all of the vector fields and symmetry reduction of the equation with nonlinearity are constructed. In particular, an exact solution is provided by using the ansatz method. In addition, other types of exact solution are obtained via the invariant subspace method. Finally, conservation laws for this equation are derived.
It is known that the classical Burgers equation (BE) is one of the better known of the nonlinear evolution equations. It comes up in various areas of sciences, in particular in physical fields. This equation can be derived from Navier-Stokes equation. Various methods have been used in the literatures to investigate these types equations (see Refs. [1–3] and the references therein).
In addition, fractional differential equations (FDEs) have been paid much attention in many fields. Therefore, how to get exact solutions of FDEs becomes the key step to better under the real world. Some methods have been developed to deal with FDEs, such as the adomian decomposition method,[4] variational iteration method,[5] homotopy perturbation method,[6] invariant subspace method,[7] symmetry analysis,[8–18] and other approaches.
In Ref. [8], the authors studied nonlinear anomalous diffusion equations with time fractional derivatives. They derived Lie point symmetries of these equations and obtained exact solutions of the nonlinear anomalous diffusion equations. In Ref. [9], the authors considered time fractional generalized Burgers and Korteweg-de Vries equations and derived their Lie point symmetries. In Refs. [10–11], fifth-order KdV FDEs are studied using the Lie symmetry analysis. One of the authors and his co-author studied fractional STO equation, perturbed Burgers equation, and KdV equation.[12–14] In Refs. [15–16], the authors studied the conservation laws of fractional equation. In view of the importance of FDEs, it is necessary for us to look for more properties of FDEs.
This paper is continuation of our previous work.[10–15] In this paper, we apply the Lie group method to analyze a fractional order nonlinear Burgers equation of the form
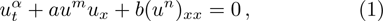
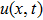
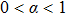
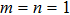
The paper is organized as follows. In Sec.
In this section, we will study the invariance properties of the time fractional generalized Burgers equation with full nonlinearity.
We employ Lie symmetry method to Eq. (
In this section, we aim to construct the solitons solution of Eq. (
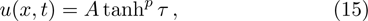
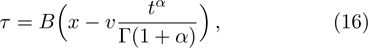
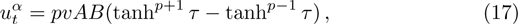
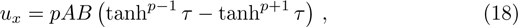
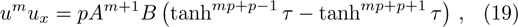
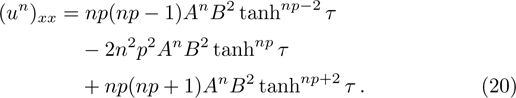
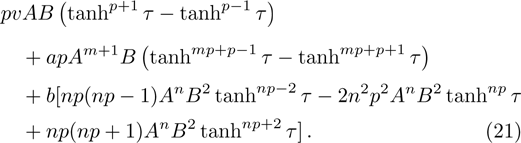
Considering the exponents mp + p + 1 and np + 2, or the exponents mp + p − 1 and np, one can get


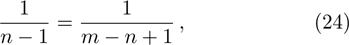



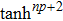
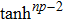
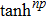
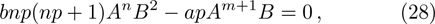
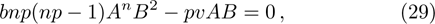
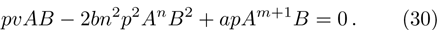

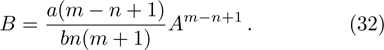
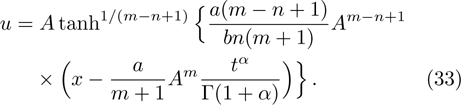
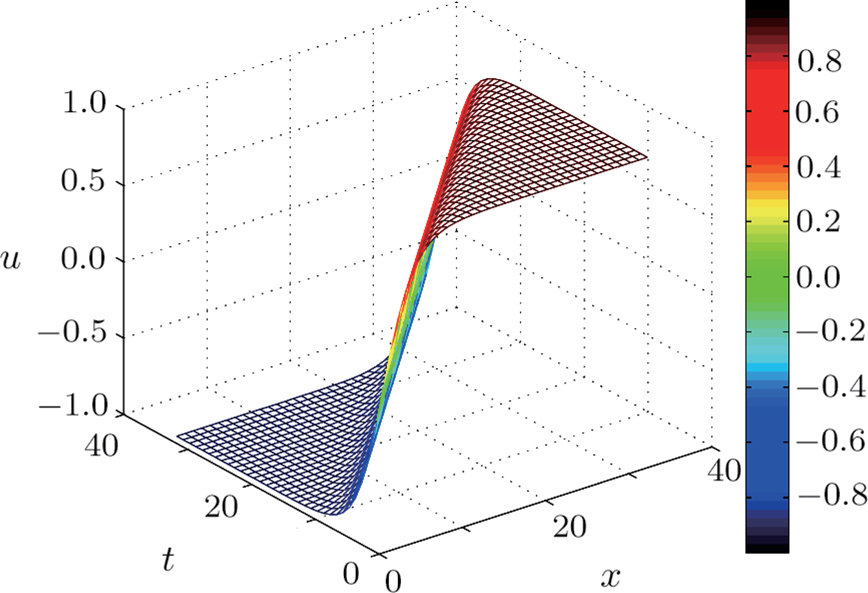
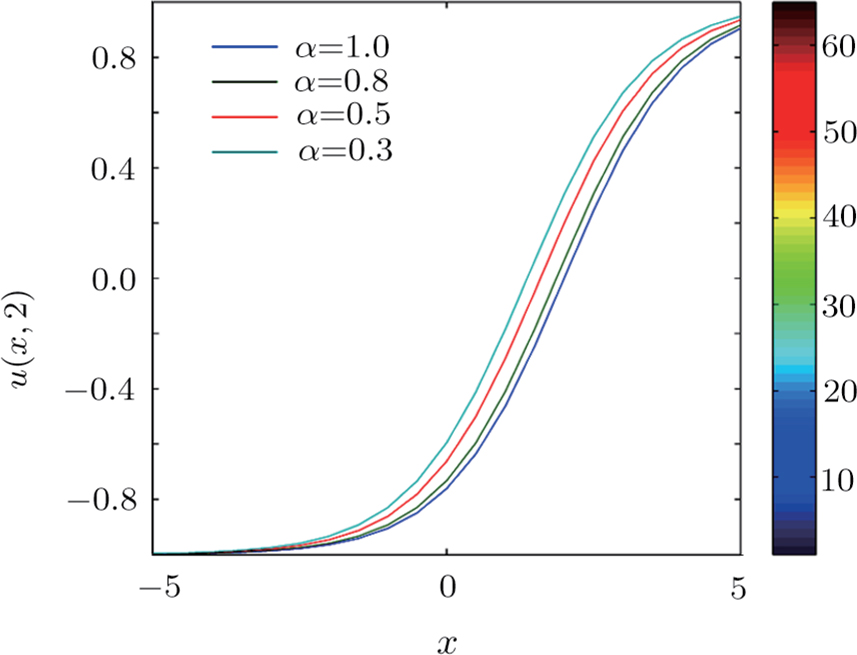
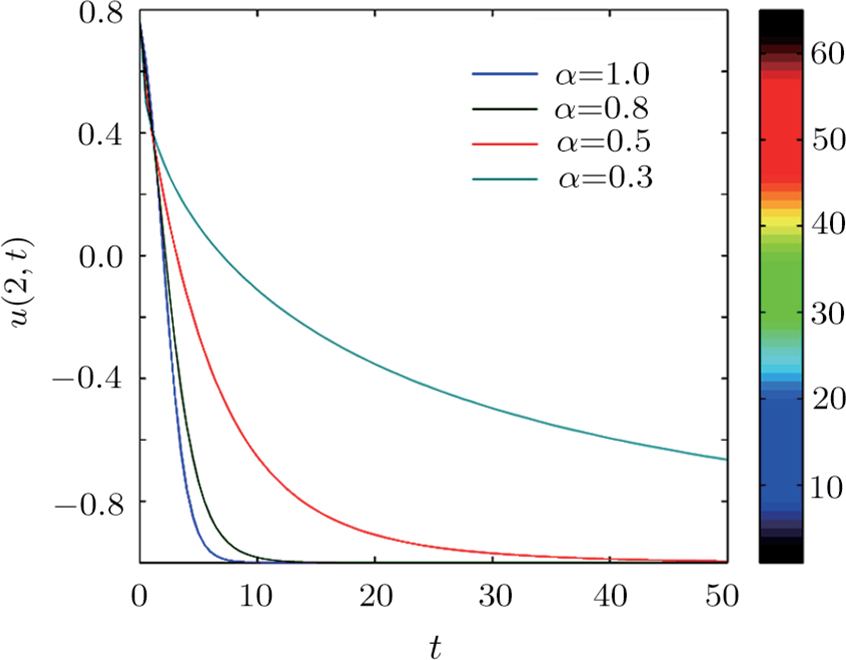
This section shows some numerical solutions of the time fractional generalized Burgers with full nonlinearity. We consider the case when m = n = 2, b = 1, a = 3, A = 1, B = 1/2.
Figure
In this section, we consider exact solution via the invariant subspace method[7] for the special case m = n = 1. It is clear that it has an invariant subspace 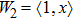
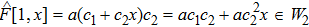
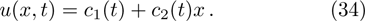
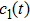
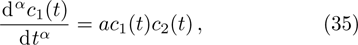
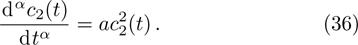
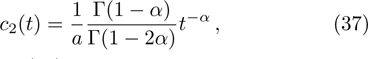

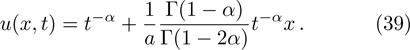
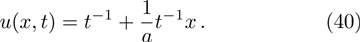
In the present section, we will deal with conservation laws for Eq. (
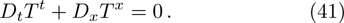
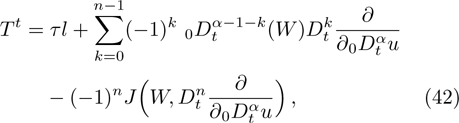
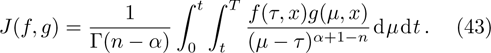
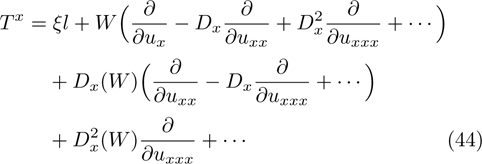
For any generator X and any solution of of Eq. (
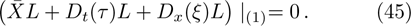
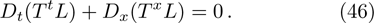
Using Eqs. (
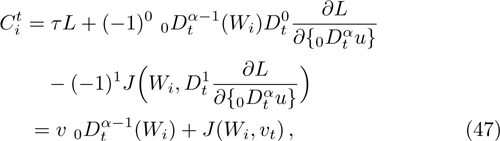
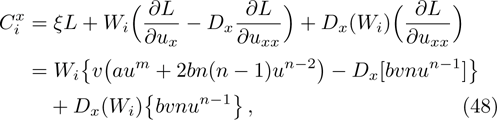
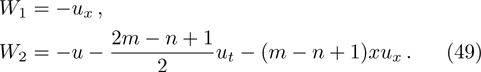
For example, 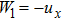
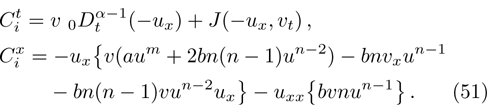
In this article, the time fractional generalized Burgers equation with nonlinearity is considered. Its Lie point symmetries were also derived. It was shown that the underlying symmetry algebra is two dimensional. Note that if α = 1 and n = m = 1, the transformed equations can be reduced to integer order ones. The case 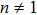
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] |