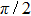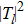† Corresponding author. E-mail:
Certain broad low-energy peaks caused by a single partial wave in total cross sections are explained in terms of phase shifts. Such peaks have been associated with the real part of a Regge pole trajectory, having a maximum near an integer value of the angular momentum quantum number. At the peak energies, the pertinent partial-wave phase shift was shown to have a local maximum near a value 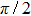
In an earlier publication[1] the authors showed that certain broad peaks in the total cross section could not be explained as resonance phenomena in the sense of long-lived quasi-bound states. One could see a correlation with complex-angular momentum pole positions (Regge poles) behaviors as functions of the energy (Regge trajectories).[1–2] The pole trajectories were seen to turn in the complex angular momentum l-plane, with Re l having a maximum close to an integer value as function of energy. Regge trajectories turning in the complex angular momentum l-plane were studied in Ref. [2].
Resonances in single-channel scattering are difficult to detect and identify experimentally for collision systems with large masses; see e.g. Toennies et al. in Ref. [3]. Scattering experiments with atomic particles are most sensitive to the broader resonances in a total cross section, with energies near the top of the centrifugal barrier. Such resonances may be mixed with non-resonance states of the type mentioned in Ref. [1]. Sharp resonances due to tunneling through the barrier and back again give negligible contribution to the cross sections but play a dominant role in predissociation spectroscopy; see e.g. Kolos and Peek, Bernstein.[3] In ion-atom systems the number of partial waves increases in comparison with atom-atom scattering; see Konrad and Linder in Ref. [3].
Recent experiments on electron-atom resonances, forming negative ions (anions), focus on electron affinities; see Walter et al. (2011) in Ref. [4]. Laser spectroscopy techniques seem to be the primary tools (Calbrese et al. (2005) in Ref. [4]). Electron transfer via (somewhat more complex) anions is among the most fundamental of chemical reactions and features prominently in all branches of chemistry; see Bull et al. (2015) in Ref. [4].
In the present note a potential model relevant for electron-atom scattering is used. The relevant “resonance” peaks in total scattering cross section are explained in terms of scattering phase shifts. The partial-wave analysis of scattering cross sections associate the scattering dynamics with phase shifts, one for each partial wave. The phase shift can be obtained from the regular solutions of the Schrödinger equation. Resonance phenomena are explained in terms of phase shift behaviors in many text books.[5–8] In the low-energy limit resonant phase shifts, due to attractive potentials, typically approach positive values 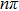
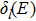
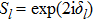
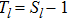
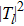
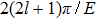
The rational function Thomas-Fermi potential (RTF) used for illustration of phase-shift behaviors has two adjustable parameters which can be adjusted to confirm a couple of experimentally measurable resonances in a reasonable way. It has been applied with some success in various calculations of electron-atom total cross sections.[1–2] Several anion states, identified by laser spectroscopy techniques,[4] have been interpreted as scattering resonances.[2] However, relevant scattering cross section measurements showing clearly resolved sharp resonances are hard to find in the literature.
The main purpose of this note is to make clear that certain broad peaks in the total cross section as function of scattering energy may not be proper resonances. There is a similarity between such broad peaks and so-called zero-momentum (quasi-) resonances appearing in connection with Levinson’s theorem,[6–8] saying that for particular potentials the zero-energy phase shift approaches an odd (rather than an even) multiple of 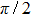
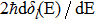
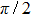
Section
By introducing a dimensionless radial variable 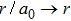
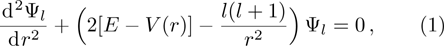

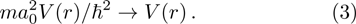
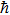
The regular solution Ψl satisfies the scattering boundary conditions that define the scattering matrix elements Sl,[8] i.e.
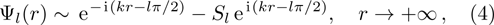

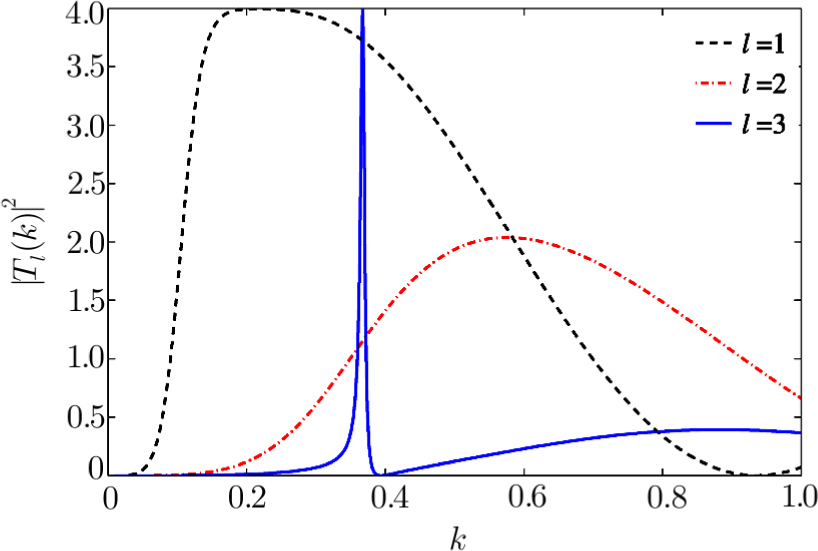
The transition matrix elements Tl are given by
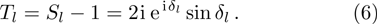
The phase shifts δl are real and the maxima of 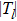
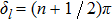
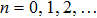
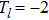
The rational function Thomas-Fermi (RTF) potential[1–2] used for illustrating an electron-atom interaction has a Coulomb attraction near the origin but adopts an attractive polarization interaction at long range. The dimensionless form of the RTF potential used here is given by[2]:
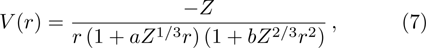
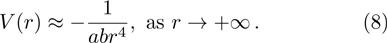
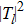
A phase shift behavior in the range 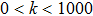
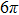
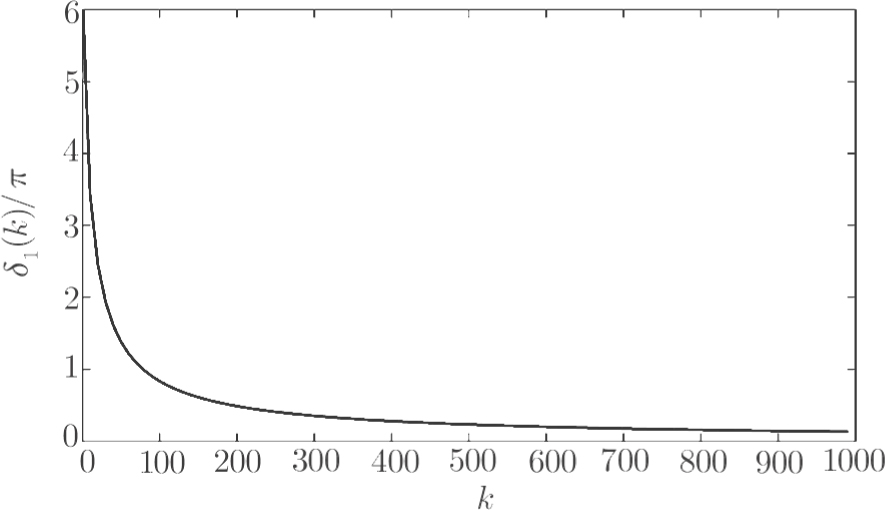 | Fig. 1 A typical phase shift behavior for a wide range of k-values. The RTF potential is defined by a = 0.19, with Z = 63 and l = 1. |
On a more detailed level, for scattering wave numbers in the range 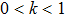
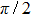
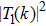
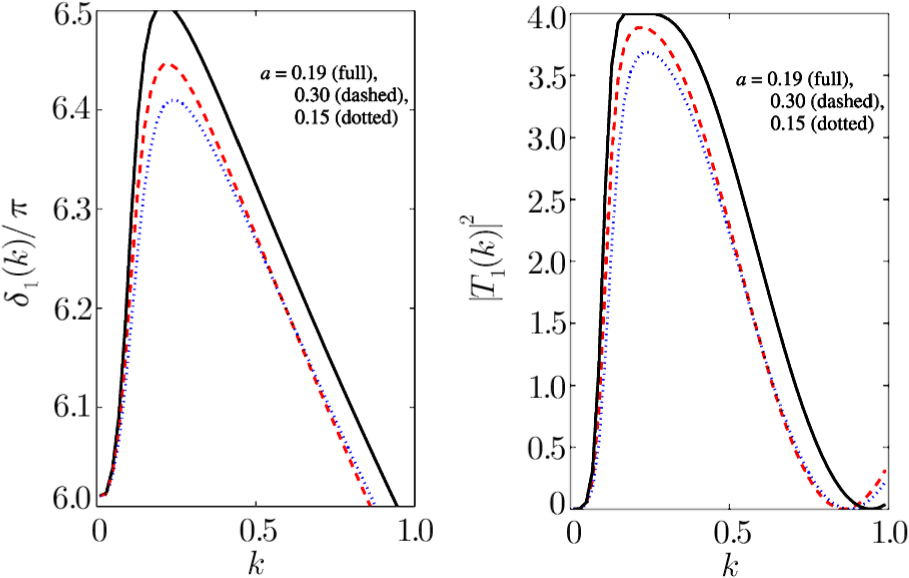 | Fig. 2 Particular low-energy phase shifts as functions of k. The RTF potentials are defined by a = 0.15, 0.19, and 0.30, with Z = 63 and l = 1. |
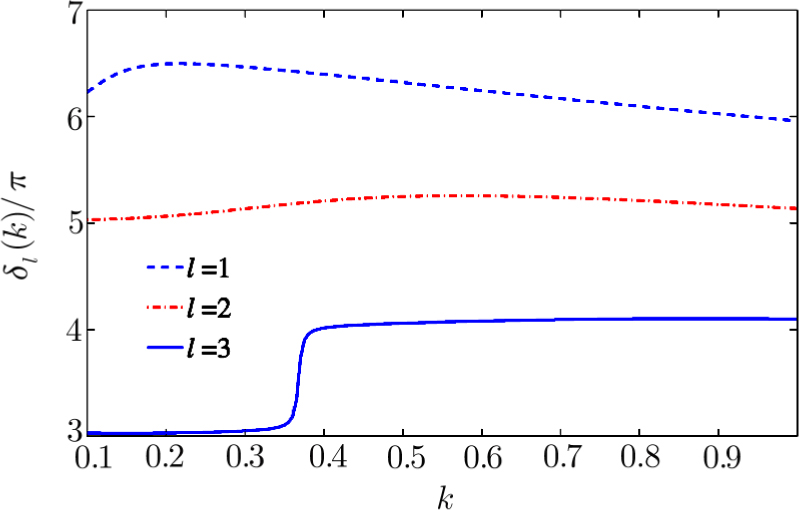
By fixing the value a = 0.19 for the RTF potential and comparing the phase shifts for l = 1, 2, and 3, one obtains Fig. 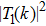
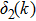
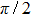
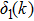
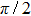
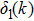
The phase shift 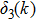
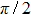
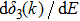
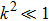
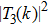
Significant, low-energy peaks in the total cross section may be observed that are not resonances. This is explained in terms of particular phase shift behaviors, not generally seen for arbitrary potential parameters. The responsible phase shift stays close to an odd integral multiple value of 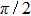
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] |