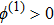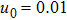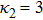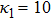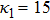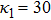The propagation of ion-acoustic waves^[1–4] in electron-ion (EI) plasmas has received a great deal of renewed interest because of their vital role in understanding different kinds of nonlinear electrostatic structures (viz. solitary waves, shock structures, double layers, etc.^[5–18]) observed in space^[19–21] and laboratory devices.^[22–24] The existence of heavy ions in astrophysical plasmas has been confirmed experimentally by detecting a noble gas molecular heavy ion in the crab nebula,^[25] our (Milky Way) Galaxy,^[26] polar region of neutron stars,^[27] active galactic nuclei,^[28] pulsar magnetosphere,^[29] and the early universe,^[30] etc.

The particle distribution near equilibrium is often considered to be Maxwellian for the modeling of different plasma systems. However, for many space plasma environments, it has been proven that the presence of the heavy ion and electron populations are far off from their thermal equilibrium state. The effects of external forces or wave particle interaction in numerous space^[31–32] and laboratory^[33–34] plasma situations indicate the existence of highly energetic (super-thermal) particles. The existence of accelerated, energetic (super-thermal) particles in the measurement of electron distribution in near-Earth space environments^{[32, 35–36]} suggests a significant deviation from Maxwellian equilibrium. So for a proper treatment of a plasma system with super-thermal electrons, one should not consider Maxwellian distribution function (DF), but other kind of non-Maxwellian DF like super thermal (κ) DF.^[37–39] The latter is given by

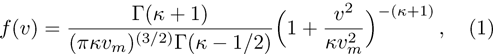
Recently, a numerous investigations have been made by many authors on ion-acoustic solitary waves (IASWs) with single-temperature super-thermal (kappa distributed) electrons.^[44–46] Schippers et al.^[47] have combined a hot and a cold electron component, while both electrons are kappa distributed and a best fit for the electron velocity distribution is found. Baluku et al.^[48] used this model for the study of ion-acoustic solitons in a plasma with two-temperature kappa distributed electrons. Pakzad^[49] studied a dissipative plasma system with super-thermal electrons and positrons, and found that the effects of ion kinematic viscosity and the super-thermal parameter on the ion-acoustic shock waves. Tasnim et al.^[50–51] also considered two-temperature non-thermal ions, and discussed the properties of dust-acoustic solitary waves and double layers. Masud et al.^[52] have studied the characteristics of DIA shock waves in an unmagnetized dusty plasma consisting of negatively charged static dust, inertial ions, Maxwellian distributed positively charged positrons, and super-thermal electrons with two distinct temperatures. Lu et al.^[53] have examined the electron-acoustic waves in an electron-beam plasma system containing cold and hot electrons. El-Taibany et al.^[54] have made stability analysis of dust-ion acoustic solitary waves in a magnetized multicomponent dusty plasma containing negative heavy ions and stationary variable-charge dust particles. Shahmansouri^[55] investigated the basic properties of ion-acoustic waves in an unmagnetized plasma containing cold and hot ions with kappa distributed electrons. Ema et al.^[56–57] studied the effects of adiabacity on the heavy ion acoustic (HIA) solitary and shock waves in a strongly coupled nonextensive plasma. They observed that the roles of the adiabatic positively charged heavy ions, and nonextensivity of electrons have significantly modified the basic features (viz. polarity, amplitude, width, etc.) of the HIA solitary/shock waves. Hossen et al.^[58–60] considered positively charged static heavy ions in a relativistic degenerate plasma and rigorously investigated the basic features of solitary and shock structures. Shah et al.^[61–62] investigated the basic features of HIA solitary and shock waves by considering both planar and nonplanar geometry.

We expect that dynamical heavy particles and higher order nonlinearity play an important role in modifying the basic non-linear features of ion-acoustic waves propagating in space and laboratory plasmas. Therefore, our main objective in this work is to investigate the effects of dynamics of heavy ions and higher non-linearity on (HIAWs) by deriving Korteweg-de Vries (K-dV), modified K-dV (MK-dV) equation, and higher order MK-dV (HMK-dV) and also is to consider the dynamics of heavy particles to describe heavy ion acoustic solitary waves (HIASWs) in such plasma system under consideration.

The manuscript is organized as follows. The basic equations are provided in Sec. 2. Three different types of nonlinear equations, namely K-dV, MK-dV, and HMK-dV are derived and analyzed analytically and numerically in Sec. 3. A brief discussion is finally presented in Sec. 4.

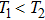
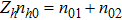
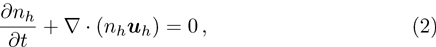
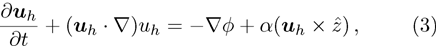
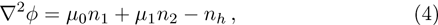
We consider a three component magnetized plasma system containing positively charged heavy ions and kappa distributed electrons with two distinct temperatures T₁ and T₂ (). Therefore, at equilibrium, we have , where Z_h (n_h0) is charge state (equilibrium number density) of the heavy ion species, and n₀₁ (n₀₂) is the equilibrium electron number density at temperature T₁ (T₂). The dynamics of the heavy ion-acoustic waves, whose phase speed is much smaller (larger) than electron (heavy ion) thermal speed, is described by the normalized equations in the form

The normalized cold and hot electron number densities n₁ and n₂ are, respectively given by

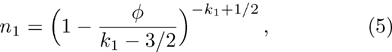
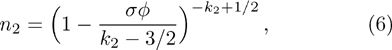
To study nonlinear propagation, we now consider different orders of nonlinearity by deriving and analyzing K-dV, MK-dV, and HMK-dV equations to identify the basic features of HIASWs formed a magnetized space plasma system containing dynamical heavy ions and kappa distributed electrons of two distinct temperatures.

3.1 K-dV Equation

To derive the K-dV equation, we use the reductive perturbation method, which lead to the stretched co-ordinates:^[63–64]

where V_p is the phase speed of the HIAWs, ϵ is a smallness parameter measuring the weakness of the dispersion , and l_x, l_y, and l_z are the directional cosines of the wave vector (so that ), as well as leads to the expansion of the perturbed quantities n_h, u_h, and ϕ in power series of ϵ:

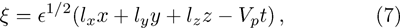
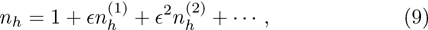
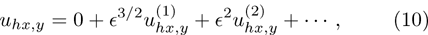
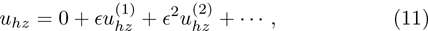
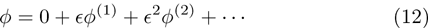
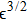
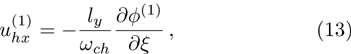
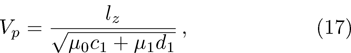
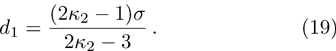
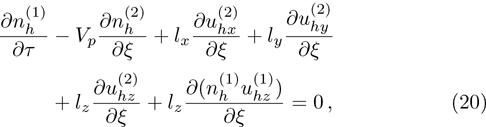
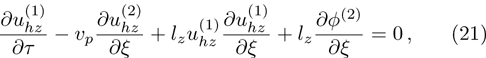
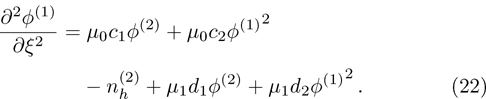
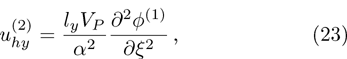
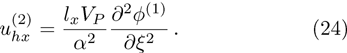
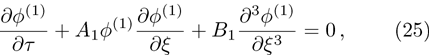
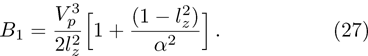
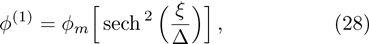
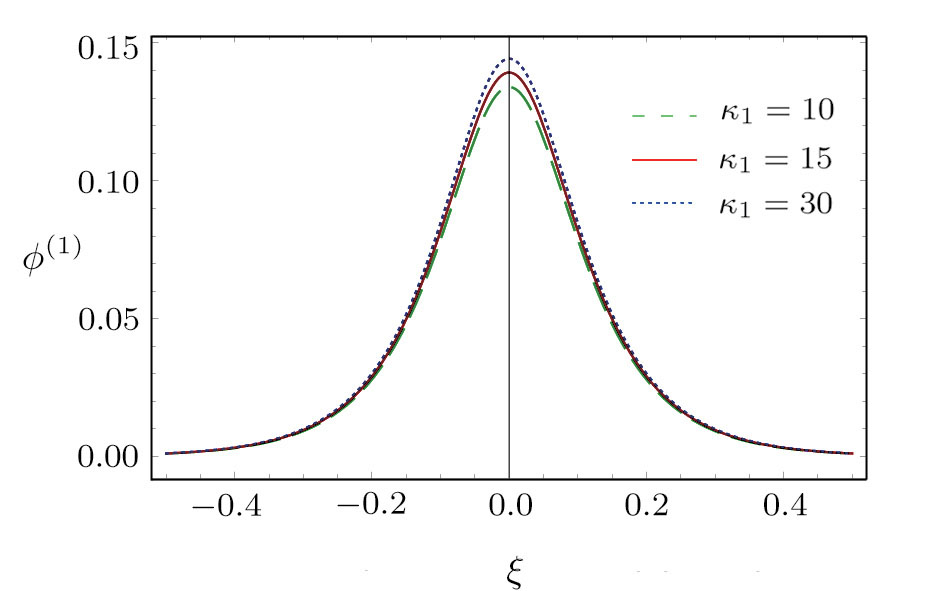
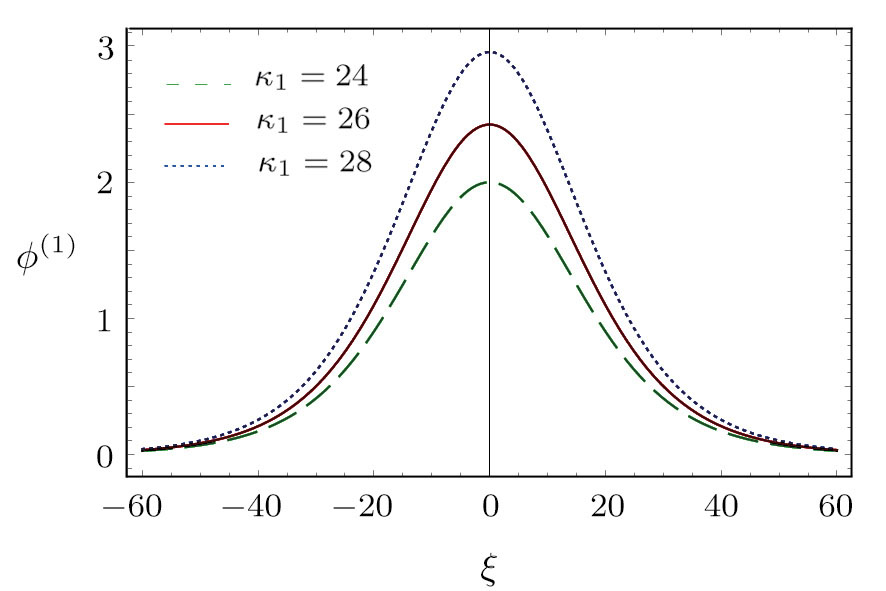Now, substituting Eqs. (7)–(12) into Eqs. (2)–(4), and then taking the terms containing from Eqs. (2) and (3), and ϵ from Eq. (4), we obtain

where

We note that Eq. (17) describes the linear dispersion relation for the propagation of the HIAWs in the magnetized plasma under consideration and that (where δ is the angle between the directions of external magnetic field and wave propagation). To the next higher order of ϵ, we again substitute Eqs. (7)–(12) into Eqs. (2), z-component of Eq. (3), and Eq. (4) and take the terms containing from Eq. (2) and z-component of Eq. (3), and ϵ² from Eq. (4). We then use Eqs. (15)–(17) to obtain a set of equations in the form

On the other-hand, substituting Eqs. (7)–(11) into x- and y-components of Eq. (3), and taking the terms containing ϵ², we get

Now, combining Eqs. (20)–(24), we have an equation in the form

where

Equation (25) is the K-dV equation describing the nonlinear dynamics of the HIASWs. Now, using the appropriate boundary conditions, viz. ϕ = 0, , and at , the stationary solitary wave solution of Eq. (25) is given by

where is the amplitude, and is the width of the HIASWs. To obtain the basic features (viz. polarity, amplitude, and width) of the ESPPs, we have numerically analyzed the solution, Eq. (28) for different plasma situations. The results are displayed in Figs. 1–10, which clearly indicate that

Fig. 1

	Figure Option ViewDownloadNew Window
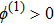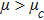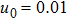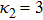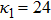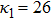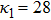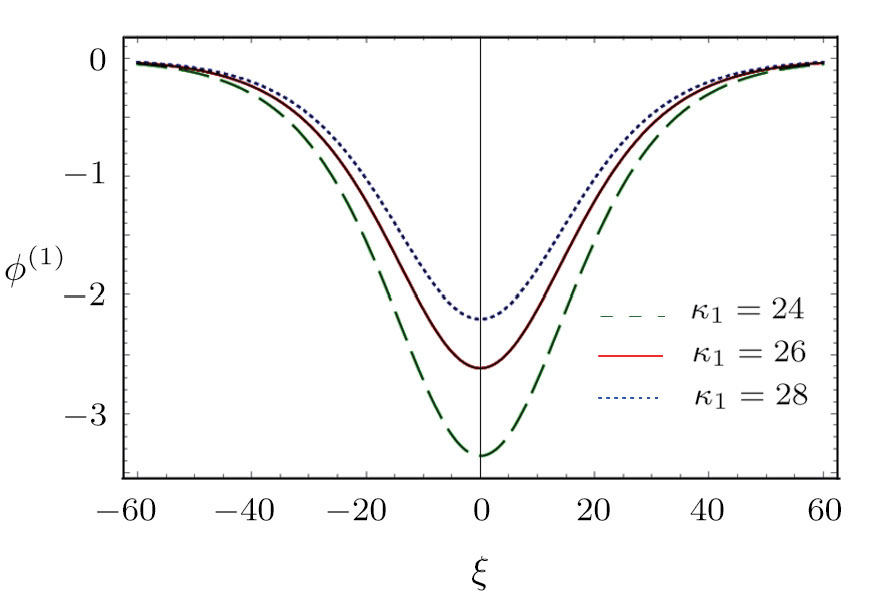	Fig. 1 (Color online) The electrostatic solitary potential profiles (ESPPs) with for , , σ = 0.25, μ = 0.7, , δ = 15, α = 0.5, (dashed curve), (solid curve), and (dotted curve).

Fig. 2

	Figure Option ViewDownloadNew Window
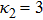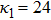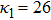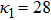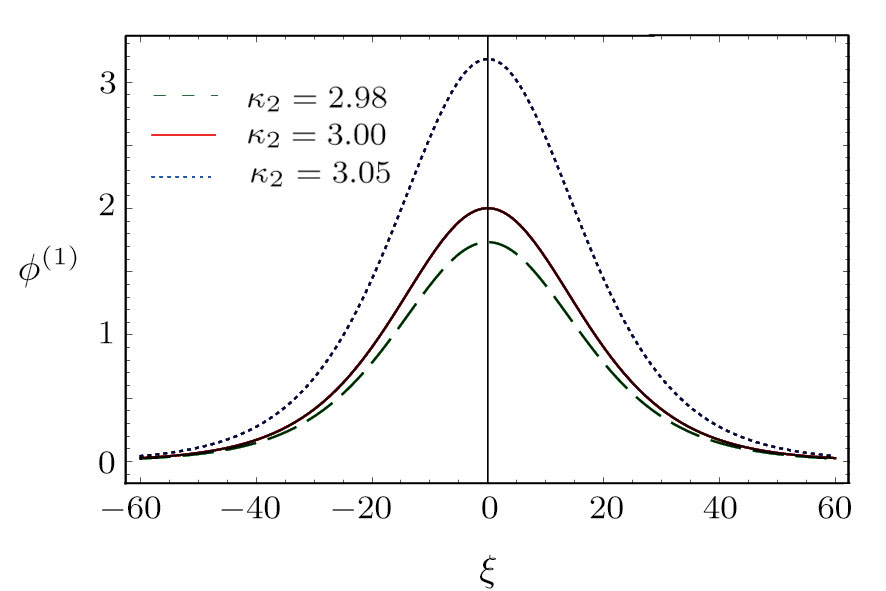	Fig. 2 (Color online) The ESPPs with for , , σ = 0.25, μ = 0.7, , δ = 15, α = 0.5, (dashed curve), (solid curve), and (dotted curve).

Fig. 3

	Figure Option ViewDownloadNew Window
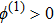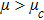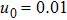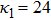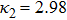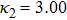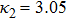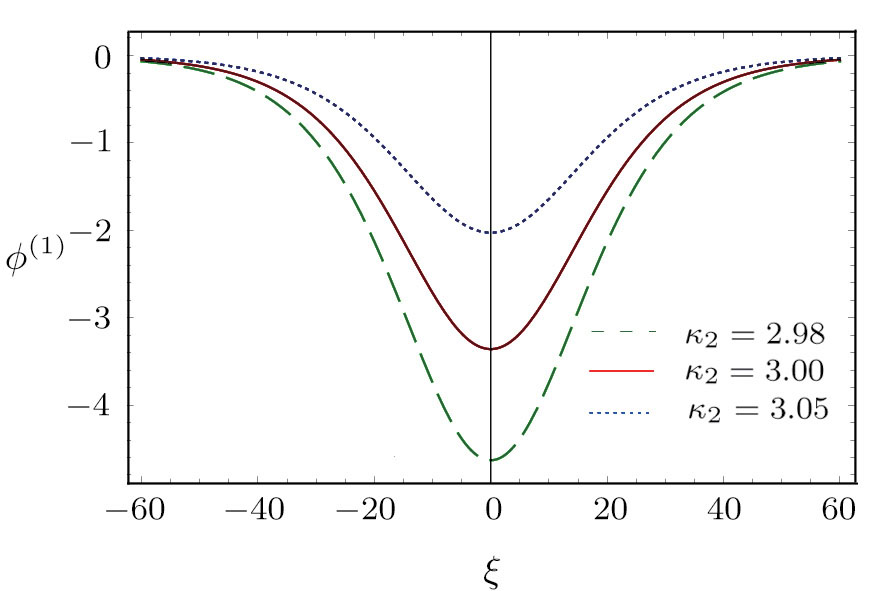	Fig. 3 (Color online) The ESPPs with for , , σ = 0.25, μ = 0.7, , δ = 15, α = 0.5, (dashed curve), (solid curve), and (dotted curve).

Fig. 4

	Figure Option ViewDownloadNew Window
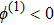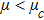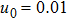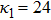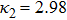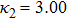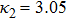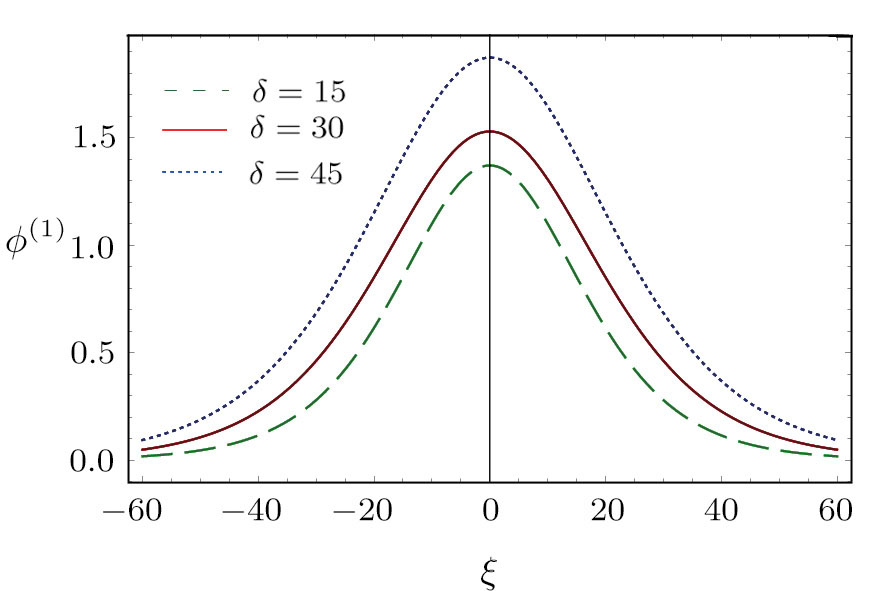	Fig. 4 (Color online) The ESPPs with for , , σ = 0.25, μ = 0.7, , δ = 15, α = 0.5, (dashed curve), (solid curve), and (dotted curve).

Fig. 5

	Figure Option ViewDownloadNew Window
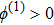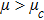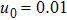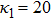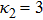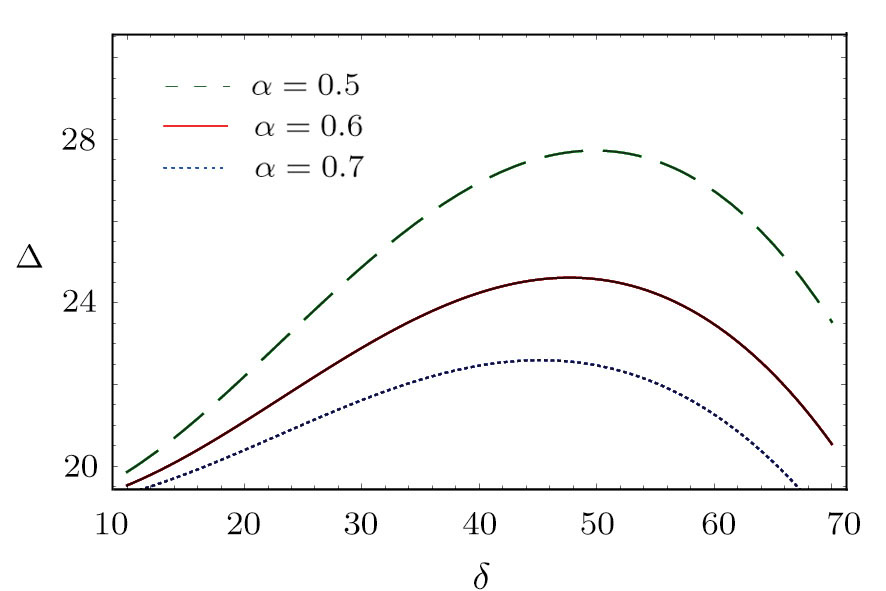	Fig. 5 (Color online) The ESPPs with for , , σ = 0.25, μ = 0.7, , , α = 0.5, δ = 15 (dashed curve), δ = 30 (solid curve), and δ = 45 (dotted curve).

Fig. 6

	Figure Option ViewDownloadNew Window
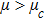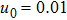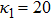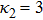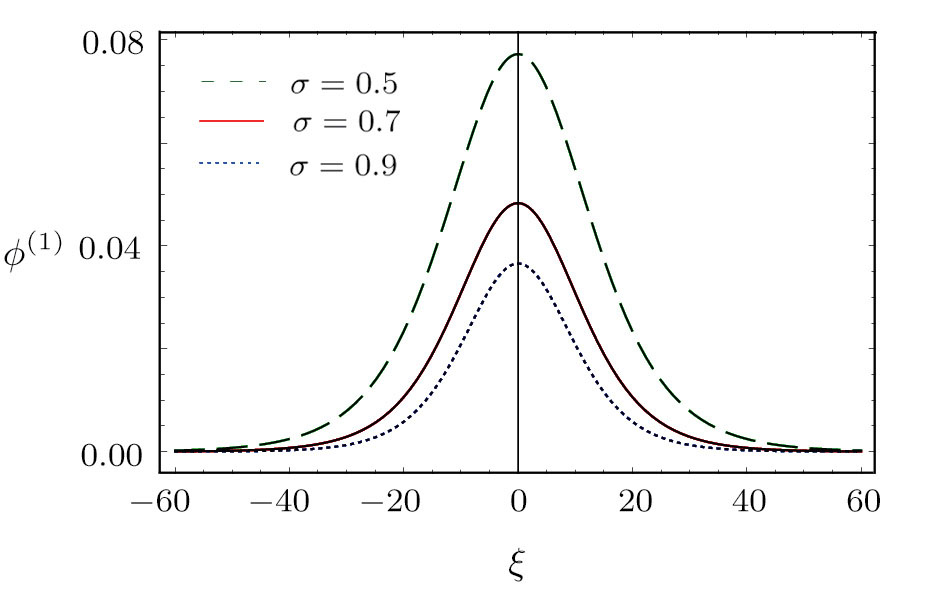	Fig. 6 (Color online) The width of the ESPPs for , , σ = 0.25, μ = 0.7, , , α = 0.5 (dashed curve), α = 0.6 (solid curve), and α = 0.7 (dotted curve).

Fig. 7

	Figure Option ViewDownloadNew Window
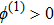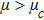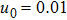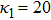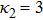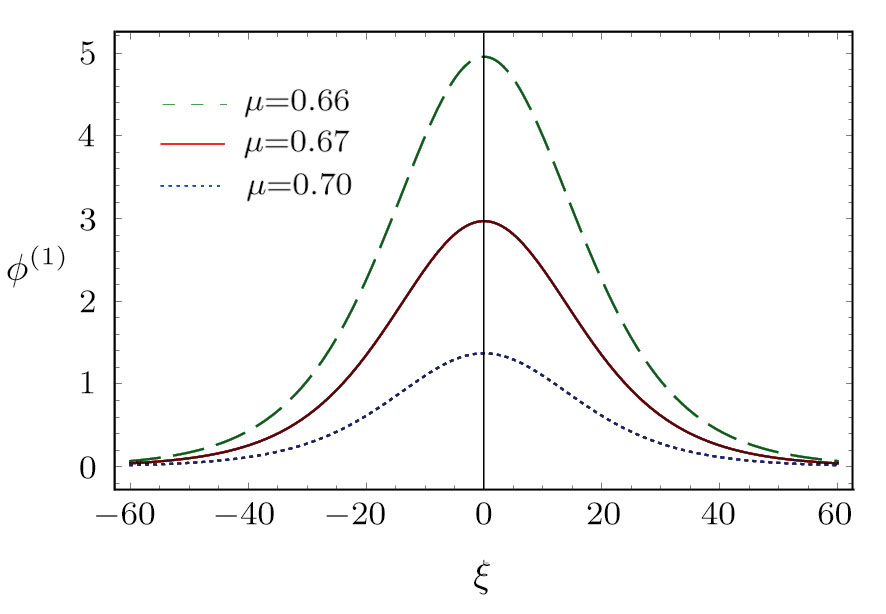	Fig. 7 (Color online) The ESPPs with for , , δ = 15, μ = 0.7, , , α = 0.5, σ = 0.5 (dashed curve), σ = 0.7 (solid curve), and σ = 0.9 (dotted curve).

Fig. 8

	Figure Option ViewDownloadNew Window
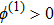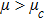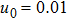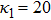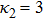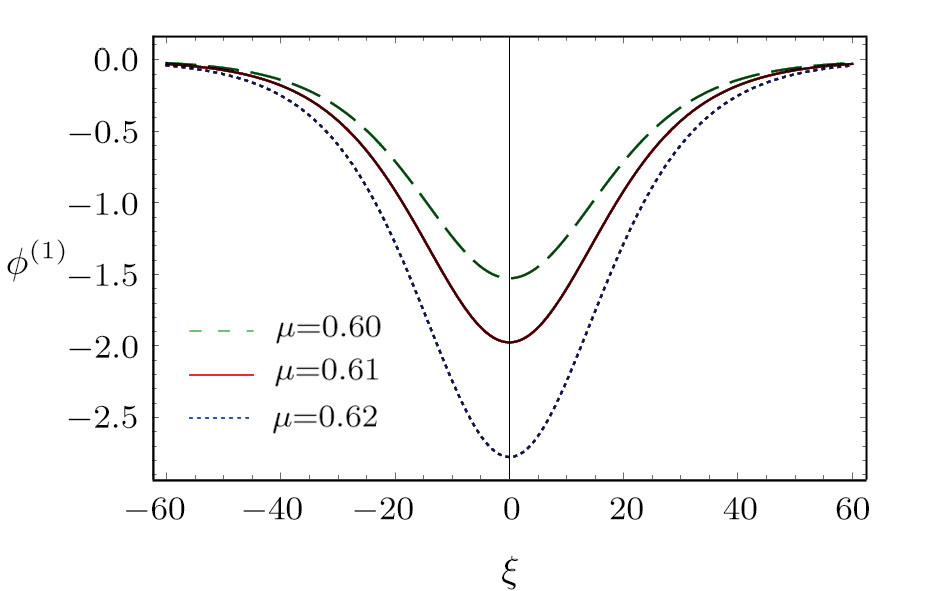	Fig. 8 (Color online) The ESPPs with for , , δ = 15, σ = 0.25, , , α = 0.5, μ = 0.66 (dashed curve), μ = 0.67 (solid curve), and μ = 0.70 (dotted curve).

Fig. 9

	Figure Option ViewDownloadNew Window
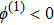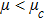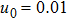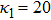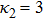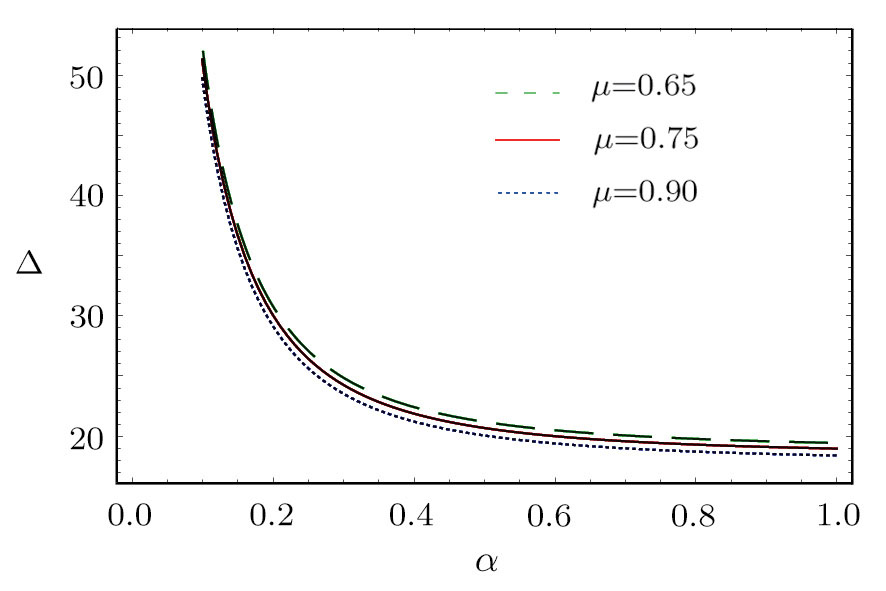	Fig. 9 (Color online) The ESPPs with for , , δ = 15, σ = 0.25, , , α = 0.5, μ = 0.60 (dashed curve), μ = 0.61 (solid curve), and μ = 0.62 (dotted curve).

Fig. 10

	Figure Option ViewDownloadNew Window
	Fig. 10 (Color online) The width of the ESPPs with 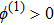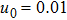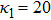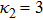for , δ = 15, σ = 0.25, , , α = 0.5, μ = 0.65 (dashed curve), μ = 0.75 (solid curve), and μ = 0.90 (dotted curve).

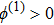
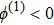
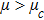
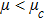
(i) The ESPPs with () exist for () as shown in Figs. 1–4, 8, and 9.

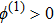
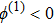
(ii) The amplitude and width of the ESPPs (with both and ) increase with the increase in κ₁, κ₂, and δ as shown in Figs. 1–5.

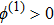
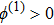
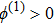
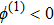
(iii) The width of the ESPPs (with ) increases (decreases) with the increase in δ for its lower (upper) range, but it decreases with the increase in α as shown in Fig. 6; (iv) The amplitude and width of the ESPPs [with ] increase with the decrease in σ as shown in Fig. 7; (v) The amplitude and width of the ESPPs (with both and ) decrease with the increase in μ as shown in Figs. 8 and 9.

(vi) the width of the ESPPs (with 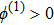) decreases with the increase in μ as shown in Fig. 10.

3.2 MK-dV Equation

To derive the MK-dV equation we use the same stretched co-ordinates defined by Eqs. (7) and (8), but the different types of expansion of the dependent variables:

Now, substituting Eqs. (7), (8), and (29)–(32) into Eqs. (2)–(4), and,and then taking the terms containing ϵ from Eq. (2) and z-component of Eq. (3), and from Eq. (4), we find the expressions for , , , , V_p, , and , which have already been given by Eqs. (13)–(17), (23), and (24). To the next higher order of ϵ, again we substitute Eqs. (7), (8), and (29)–(32) into Eqs. (2)–(4), and,and take the terms containing from Eq. (2) and the z-component of Eq. (3), and ϵ from Eq. (4). Then using the expressions for , , , , V_p, , and in these higher order equations, we obtain a set of equations:

where

To further higher order of ϵ, substituting Eqs. (7), (8), and (29)–(32) into Eqs. (2)–(4), and then taking the terms containing ϵ² from Eq. (2) and the z-component of Eq. (3), and from Eq. (4), we obtain another set of equations:

Now, combining Eqs. (38)–(40), we finally obtain the MK-dV equation:

where

To solve this MK-dV, We consider a frame (moving with speed u₀). The stationary solitary wave solution of the MK-dV equation (Eq. (41)) is given by

where is the amplitude, and is the width of HIASWs. To identify the salient features (viz. polarity, amplitude, and width) of the ESPPs, we have numerically analyzed the solution of the MK-dV equation (Eq. (45)) for different plasma parametric regimes. The results are depicted in Figs. 11–13, which clearly indicate that

Fig. 11

	Figure Option ViewDownloadNew Window
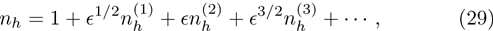
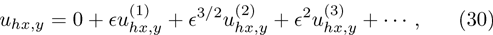
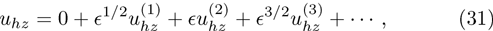
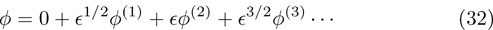
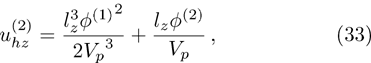
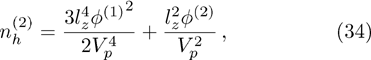
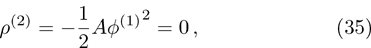
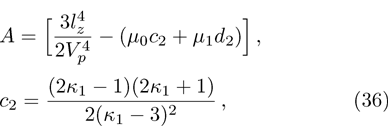
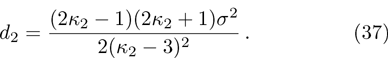
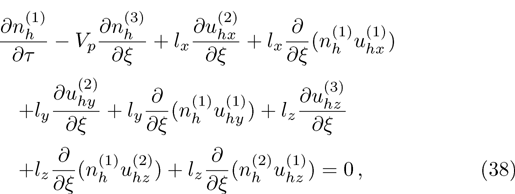
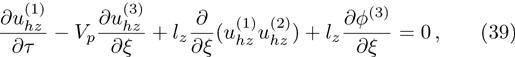
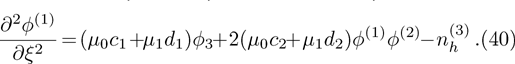
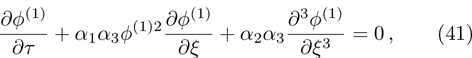
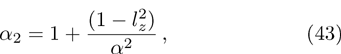
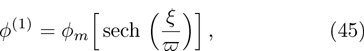
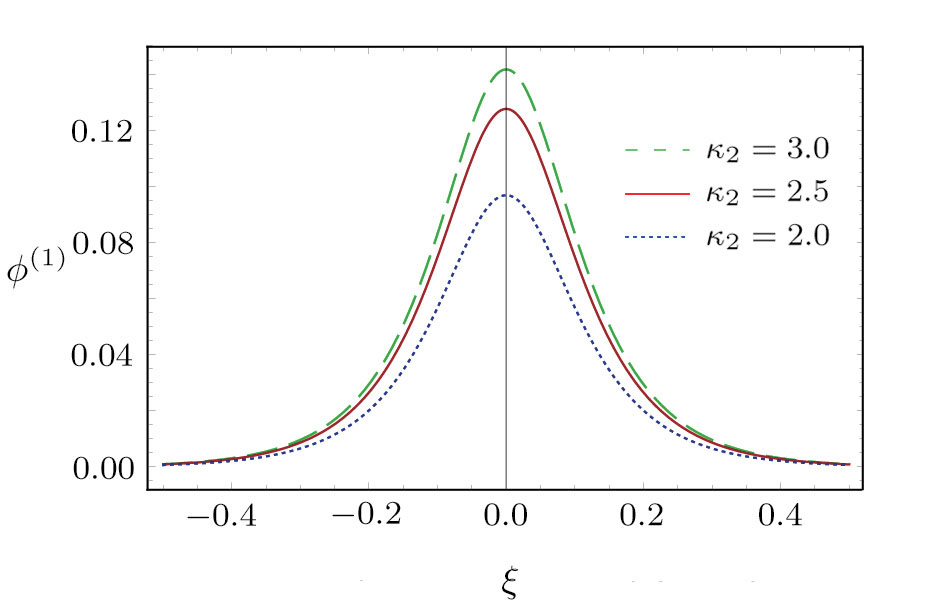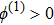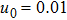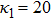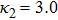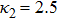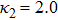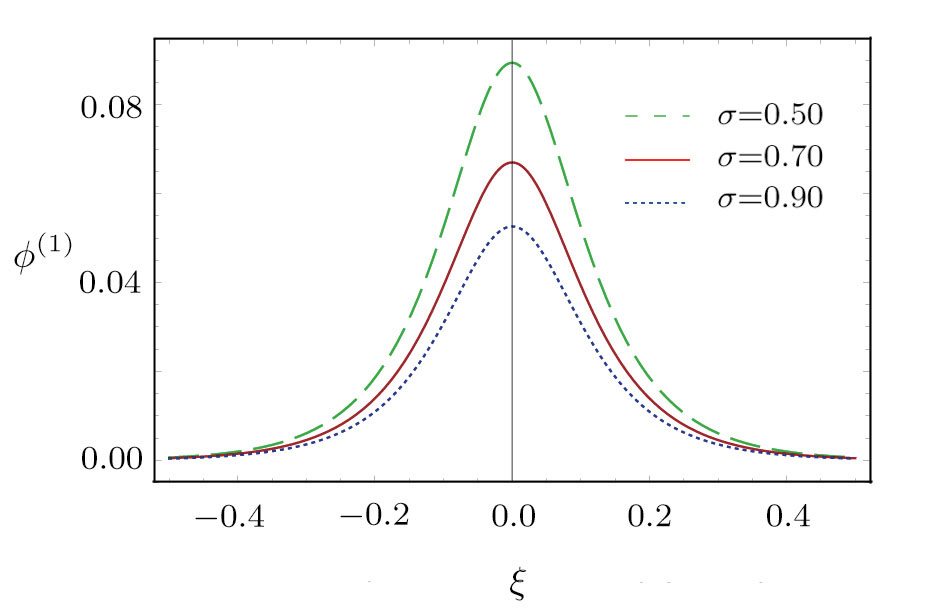	Fig. 11 (Color online) The ESPPs with for , σ = 0.25, μ =0.7, , δ = 15, α = 0.5, (dashed curve), (solid curve), and (dotted curve).

Fig. 12

	Figure Option ViewDownloadNew Window
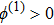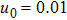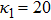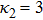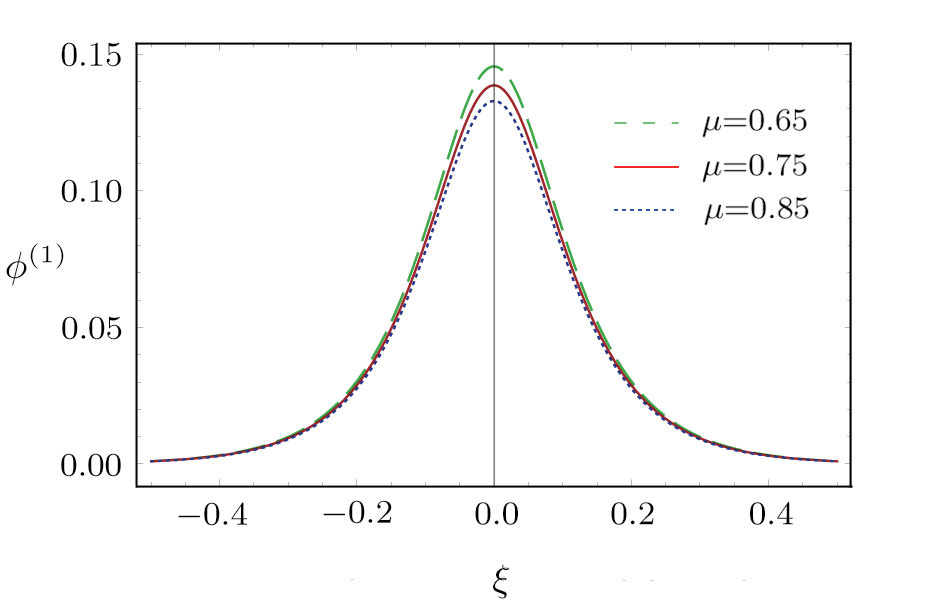	Fig. 12 (Color online) The ESPPs with for , δ = 15, μ = 0.70, , , α = 0.5, σ = 0.50 (dashed curve), σ = 0.70 (solid curve), and σ = 0.90 (dotted curve).

Fig. 13

	Figure Option ViewDownloadNew Window
	Fig. 13 (Color online) The ESPPs with 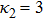for , δ = 15, σ = 0.25, , , α = 0.5, μ = 0.65 (dashed curve), μ = 0.75 (solid curve), and μ = 0.85 (dotted curve).

(i) The MK-dV equation admits solitary wave solution with 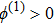only; (ii) The amplitude and width of the ESPPs increase with the increase in (κ₂) as shown in Fig. 11.

(iii) The amplitude and width of the ESPPs increase with the increase in σ as shown in Fig. 12.

(iv) The amplitude and width of the ESPPs decrease with the increase in μ as shown in Fig. 13.

3.3 HMK-dV Equation

To examine the effects of further higher order nonlinearity on the K-dV or MK-dV equations describing HIAWs in a magnetized plasma (containing containing dynamical heavy ions and bi-kappa distributed electrons of two distinct temperatures), one can derive a further higher order nonlinear equation. The latter (after performing few steps of mathematical calculations) can be directly given by^{[65, 66]}

where A₁, α₁, and α₃ are defined in deriving K-dV and MK-dV equations, , and . Equation (46) is known as higher-order MK-dV (HMK-dV) equation. The solutions of this HMK-dV equation for and are, respectively, given by^{[65, 66]}

where . We have numerically analyzed one^[47] of the two solutions of the HMK-dV equation^[46] to show how further higher order nonlinearity modifies the ESPPs obtained from the solutions of K-dV and MK-dV equations. The numerical results are shown in Fig. 14, which implies that the width and amplitude of the ESPPs slightly increase with the increase in κ₁.

Fig. 14

	Figure Option ViewDownloadNew Window
	Fig. 14 (Color online) The ESPPs (with ) for , σ = 0.25, μ = 0.7, , δ = 15, α = 0.5, (dashed curve), (solid curve), and (dotted curve).

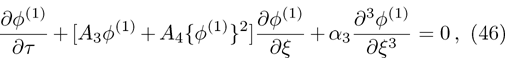
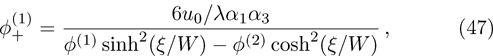
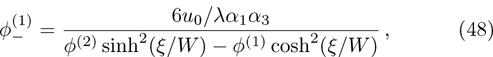
We have considered a magnetized plasma system consisting of inertial heavy ions and kappa distributed electrons of two distinct temperatures. We have derived the K-dV, MK-dV, and HMK-dV equations by using the reductive perturbation method to identify the basic features (polarity, amplitude, and width) of the ESPPs formed in such a magnetized plasma system. The results, which have been obtained from this theoretical investigation, can be pin-pointed as follows:

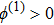
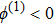
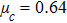
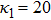
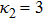
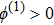
(i) The K-dV and HMK-dV equations admit HIASW solutions with either (compressive) or (rarefactive). The polarity of the HIASWs depends on the critical value μ_c (where for , , δ = 15, σ = 0.25, and α = 0.5). On the other-hand, the MK-dV equation admits only HIASW solution with (compressive).

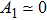
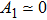
(ii) The amplitude of the K-dV solitons become infinitely large for , and thus the K-dV equation is no longer valid at , which has been avoided by deriving MK-dV and HMK-dV equations to study more highly nonlinear HIASWs.

(iii) The amplitude and width of both positive and negative HIASWs (obtained from the numerical analysis of the solution of the K-dV equation) increase with the increase in κ₁ and κ₂. However the amplitude of the positive HIASWs increases with the increase in δ. On the other-hand, the width decreases with the increase in α, and increases (decreases) with the increase in δ for its lower (upper) range.

(iv) The amplitude of the K-dV HIASWs increases with the increase in T₂ and n₀₁, but decreases with the rise of T₁ and n₀₂.

(v) The width of K-dV HIASWs rises with the increase (decrease) in n₀₁ (n₀₂).

(vi) The amplitude and the width of the MK-dV HIASWs increase with the increase in κ₂, T₂ and n₀₁, but decrease with the increase in T₁ and n₀₂.

(vii) The amplitude and the width of the HMK-dV HIASWs slightly increase with the increase in κ₁. This means that the effect of higher nonlinearity on K-dV and MK-dV HIASWs is insignificant.

To conclude, the results of our present investigation are relevant to space (viz. Saturns magnetosphere,^[43] pulsar magnetosphere,^[67] upper part of the ionosphere,^[68–70] lower part of the magnetosphere,^[68–70] etc.). The dip shape solitary structures (known as cavitons^[68–70]) observed by Freja satellite^{[68, 70]} and Viking spacecraft^[69–70] are similar to those predicted by our present theoretical investigation. We finally hope that our results should be useful in understanding the nonlinear eloctrostatic disturbances in the space plasma systems containing heavy ions and super-thermal electrons of two distinct temperatures.