† Corresponding author. E-mail:
In this article, a special type of fractional differential equations (FDEs) named the density-dependent conformable fractional diffusion-reaction (DDCFDR) equation is studied. Aforementioned equation has a significant role in the modelling of some phenomena arising in the applied science. The well-organized methods, including the 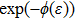
 -expansion method" target=_blank>
-expansion method" target=_blank>

Fractional differential equations are mathematical models which are appeared in the vast areas of science and engineering and great attention has been directed toward them over the last few decades. To be more specific, FDEs are the generalizations of classical differential equations which play a significant role in the mentioned areas. Fortunately, it is possible to establish a traveling wave transformation for a fractional differential equation which can convert it to an ordinary differential equation (ODE) of integer order such that the resulting ODE can be easily solved using a variety of robust methods.[1–15]
One of well-designed methods which may be employed to solve nonlinear fractional differential equations is the 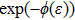
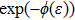
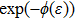
Another mathematical method which is truly robust to solve nonlinear FDEs is a modified form of Kudryashov method. Fundamental of this method is described in detail in the next sections, so here just some applications of this technique are reviewed. Korkmaz[18] utilized the modified Kudryashov method to construct the exact solutions of a family of the conformable time-fractional Benjamin-Bona-Mahony equations; and Hosseini et al.[19] constructed a series of new exact solutions of the conformable time-fractional Klein-Gordon equations using the modified Kudryashov method. More articles may be found in Refs. [20–28].
In this paper, the 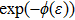
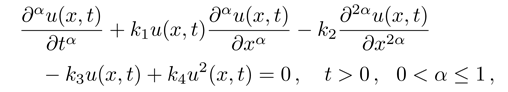
The rest of this work is as follows: In sec. 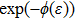
There are various definitions for the fractional derivatives. Among these, the conformable fractional derivative has gained a special interest during the last years. The αth order of the conformable fractional derivative of f can be defined as[30]
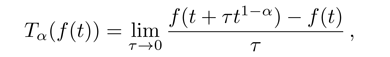
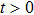
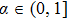
A series of the properties of conformable derivative may be listed as follows[30,32]
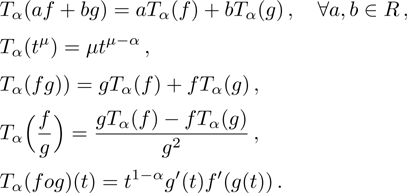
Using the transformation
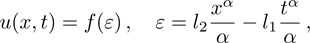
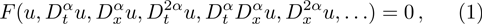
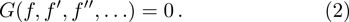
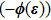
We look for an explicit solution for the Eq. (
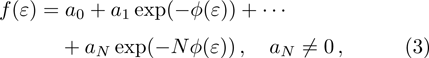
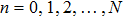
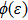
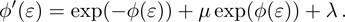
The initial steps of the modified Kudryashov method are as before. With the same transformation, the original fractional differential equation can be converted to a nonlinear ODE, which its solution is supposed to be in the form
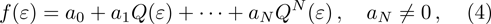
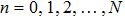
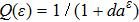
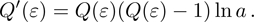
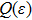
In this section, the exact solutions of density-dependent conformable space-time fractional diffusion-reaction equation will be extracted using the 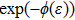
Using the transformation
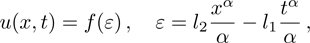
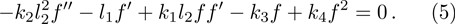
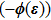
From the technique of homogeneous balance, we find N = 1. This offers a series as the following form
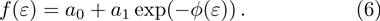
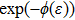
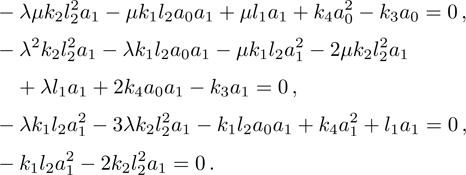
It is obvious that N = 1. Therefore, a series can be derived as follows

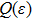
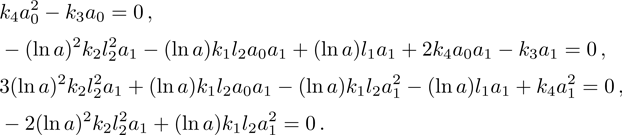
The exact solutions of density-dependent conformable space-time fractional diffusion-reaction equation have been successfully extracted using the newly well-organized techniques called the 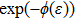
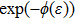
(i) The modified Kudryashov method provides more straightforward solution procedure.
(ii) The modified Kudryashov method considers an arbitrary constant 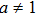
(iii) The modified Kudryashov method can be easily applied to handle the high order differential equations as illustrated by Zayed and Alurrfi.[21]
Accordingly, it is fair to say that the modified Kudryashov method can be considered as one of the best techniques to extract new exact solutions of FDEs.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] |

