| 150 t钢包自由表面旋涡的数值模拟与湍流模型的选择 |
b. 北京科技大学,冶金与生态工程学院,北京100083
b. School of Metallurgical and Ecological Engineering, University of Science and Technology Beijing,Beijing 100083,China
当流体通过小孔向外排出时,流体质点在径向某处产生逐渐偏离径向的切向转流动就是"汇流游涡"[1],也称自由表面旋涡,旋涡产生时对应的液面高度称为旋涡临界高度.在钢包非稳态浇注的末期,钢液面降低到-定的高度时,由于钢液切向速度的存在,在水口上方自由表面会形成旋涡,钢渣通过旋涡核心被卷人钢液中,随着浇注的进行最终贯通水口,进人中间包造成大量下渣,大大降低了钢的纯净度,危害钢的质量[2-3].多年来,国内外很多学者对旋涡进行了大量的理论分析和实验研究,理论研究了定常轴对称涡和非定常双胞胎涡N-S 方程的精确解[4];张涤明[5]从理论上分析了轴对称汇流的周向稳定性,得到了稳定性的频散关系,并在此基础上,对汇流成涡的机理提出了不同的见解,得到汇流周向失稳的临界雷诺数;Piva等[6]通过水模拟实验,分析了流体的不同初始切向速度和出口偏心率对旋涡临界高度的影响.商瑞等[7-8]和叶树峰等[9] 用物理实验的方法,考察了不同水口直径、渣层厚度、初始液面高度及不同水口形状等因素对临界高度的影响,得出旋涡临界高度随水口直径的增大而增大;渣在-定程度上会抑制旋涡的形成和发展,但渣层厚度对临界高度的影响不明显,与初始液面高度没有明显关系,采用缝隙式出流口时产生的临界高度明显低于采用同面积的圆形出流口时的临界验研究,但由于其流动机理复杂,仅仅通过实验分析很难说明其内部流场.
随着计算流体动力学技术的完善,采用数值模拟的方法虚拟再现自由表面旋涡的形成与发展过程,成为研究自由表面旋涡的新方向.Ka ikov 等[10]通过数值模拟的方式清晰的解释了不同因素对旋涡的影响.赵永志等[11-12]采用雷诺应力揣流模型成功的模拟出旋涡的产生和演化过程,得到旋涡是由旋转能量的局部集中造成的,并提出了涡运动机理假说.陈云良[13]用k-ε和RNG k-ε 2 种揣流模型对进水口前立轴旋涡进行数值模拟研究,用RNG k-ε 模型模拟出了漏斗形吸气旋涡,用标准k-ε 模型却没有模拟出立轴旋涡.商瑞等[14]用标准k-ε 模型模拟出钢液浇注过程的旋涡,但未用RNG k-ε 模型进行模拟.本文利用ANSYS CFX大型商业软件对某钢厂150 t 钢包非稳态浇注过程进揣流模型对其进行计算,并将计算结果进行对比分析,确定出较适宜的揣流模型,为下-步研究旋涡的行为及抑制旋涡打好基础.
1 数值模拟过程 1.1 模型假设由于实际的钢包中钢液流动是极其复杂的物理过程,因此对浇注过程中钢包内流体做出如下假设:
1) 流体的流动为恒温、不可压缩的均匀流动;
2) 流体均按均相介质处理;
3) 忽略表面渣层的影响,将液面设为自由表面.
1.2 模型控制方程分别运用k-ε 和RNG k-ε 揣流模型对钢包非稳态浇注过程中的流体流动进行模拟计算,其基本方程包括连续性方程、动量方程和揣流方程.
1) 连续性方程
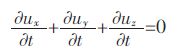
|
(1) |
式(1)中:ui (i=1,2,3)分别为三坐标轴x、y、z 方向上的速度(ux,uy,uz).
2)动量方程
x 方向:
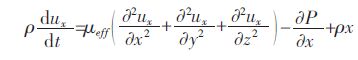
|
(2) |
y 方向:
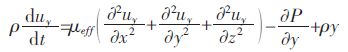
|
(3) |
y 方向:
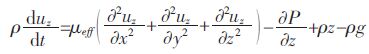
|
(4) |
式(2)、式(3)、式(4)中: ρ 为流体密度;P 为压力;μeff为有效勃性系数,其表达式为: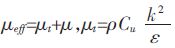
3) 揣流方程
k-ε 揣流模型:
揣动能(k)方程:
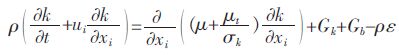
|
(5) |
揣动能耗散(ε)方程:
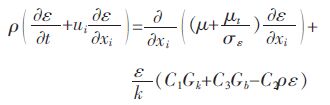
|
(6) |
RNG k-ε 揣流模型:
揣动能(k)方程:
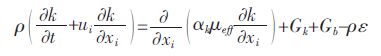
|
(7) |
湍功能耗散(ε)方程:
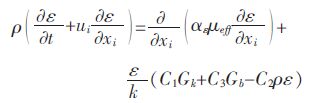
|
(8) |
式(5)-式(8)中Gk 是由于平均速度梯度引起的揣动能的产生;Gb 是由于浮力影响引起的揣动能的产生;αk 和αs 分别为揣动能和耗散率的有效普朗特数的倒数;C1、C2、C3、Cu、σk、σs 均为经验常数,采用推荐值分别为C1 =1.44、C2 =1.92、C3 =0.09、Cu =0.09、σk =1.0、σs=1.3.
1.3 钢包模型的建立根据相似原理,用缩小的模型对原型的钢液流动进行模拟,要求模型与原型中的流体满足几何相似和动力相似,在钢包浇注的过程中,主要是重力和惯性力作用占统治地位,即在几何相似的前提下,要保证模型和原型中流体的雷诺数Re 和弗鲁德准数Fr 相等,由于在浇注过程中钢水流动已经处于第二自模化区,雷诺数Re 能满足要求,所以只要保证模型与原型中的弗鲁德准数Fr 相等即可.Fr 是描述流体所受重力和惯性力之比的-个相似准数,用下式表示:
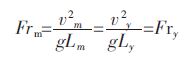
|
(9) |
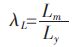
|
(10) |
式(9)和式(10)中vm、vy 为模型和原型流体的速度,m/s,g 为重力加速度,m/s2,Lm、Ly 为模型和原型的特征长度,m,λL 为比例因子.
在浇注过程中的某-时刻:
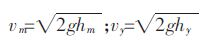
|
(11) |
式(11)中hm、hy 为此时刻模型和原型的液面高度,m.
由此得到:
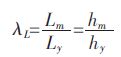
|
(12) |
即在几何相似的条件下,只要保证模型和原型的液面高度比与几何相似比相等,就能保证两者的弗鲁德准数Fr 相等,进而满足模拟要求.根据钢包原型的条件,采用几何相似比λL=1:3 来进行数值模拟计算. 模型的有关参数见表 1.
| 表1 钢包模型的相关参数 |
 |
| 点击放大 |
本模拟中水口长度取60 mm,液面高度为300 mm,为了更好的对2 种揣流模型进行比较,在计算时采用偏心率为0 的钢包模型.用ICEM CFD 软件对钢包模型进行。 形网格划分,对水口和壁面进行加密处理,生成非结构化网格,图 1 为偏心率为0 的钢包模型,共21 735 个网格单元.
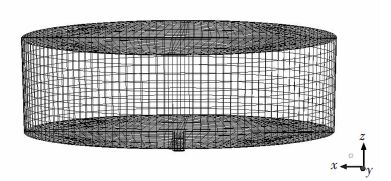 |
| 图 1 钢包模型 |
1.4 边界条件及求解控制
1) 边界条件. 流体域参考压力为1 个标准大气压,即1.01x105Pa,采用多相流模型对钢液流动进行模拟,流体为两相:液相(钢液)和气相(空气);流动模型为均相模型,即两相之间没有相对速度,只有1 个压力场和速度场; 将钢液上表面设置为自由表面,对于平行于自由表面的速度分量和其他的标量梯度均为0,垂直于自由表面的速度分量也为0. 分别选用k-ε 和RNG k-ε 揣流模型,近壁区域选用Scalable 壁面函数;流体对(钢液和空气)中的主流体设为钢液,相间传递为自由表面传递,即两相之间有明显的交界面,没有质量传输.入口为钢液的自由表面,设为开放式入口,相对压力为0,底部水口为压力出口,钢包壁面采用元滑移边界条件. 初始压力为钢水静压力,初始各方向速度均为0.
2)求解控制.求解类型为瞬态,时间步长为0.01 s,计算精度为10-4,每个时间步长最大迭代20 步,求解时间和数据保存进行动态调节,直至浇注完成.
2 数值模拟的结果与讨论 2.1 2 种浦流模型的计算结果与比较 2.1.1 自由表面旋涡演化过程的比较图 2、图 3 为分别用k-ε 和RNG k-ε 2 种揣流模型进行数值计算所得到的自由表面旋涡的演化过程. 从图 2、图 3 可看到:浇注过程中,钢液通过收缩水口汇流排出,随着液面高度的下降,钢液的位能不断的转化为钢液的动能,且由于钢液的汇流会产生偏离径向的切向流动,进而产生环量,且几何模型存在锥度及边界条件等因素的存在,加剧了流体产生偏离径向的切向流动的趋势,环量不断累积,当液面下降到-定高度时,水口上方自由表面的流体开始出现围绕中心的旋转流动,如图 2(a)、图 3(a)所示;随着出钢的进行,旋转不断加剧,液面中心出现下凹,形成旋涡,如图 2(b)、图 3(b)所示;液面高度进-步下降,空气不断地被卷入到钢液中,下凹的旋涡由弧形逐渐变为锥状,形成锥形气柱,且气柱逐渐变长变尖,气柱尖部抵达钢包底部时为旋涡发展阶段,如图 2(c)、图 3(c) 所示;由于钢液存在却性,内部流体先旋转并将旋转能量向外传递,旋涡最终发展为漏斗形,如图 2(d)、图 3(d)所示,气柱抵达水口底部,已造成大量下渣.综上所述:在同-标准下,用2 种揣流模型所计算出的自由表面旋涡的演化过程是-致的,且每阶段对应的液面高度几乎没有差别,说明2 种模型都可以用来模拟自由表面旋涡,且两者差距不明显.实际生产过程中,采用留钢操作来避免大量下渣,留钢高度应不低于旋涡发展时对应的液面高度,这样钢渣就不会进入到中间包中,为后续的生产减轻了压力.
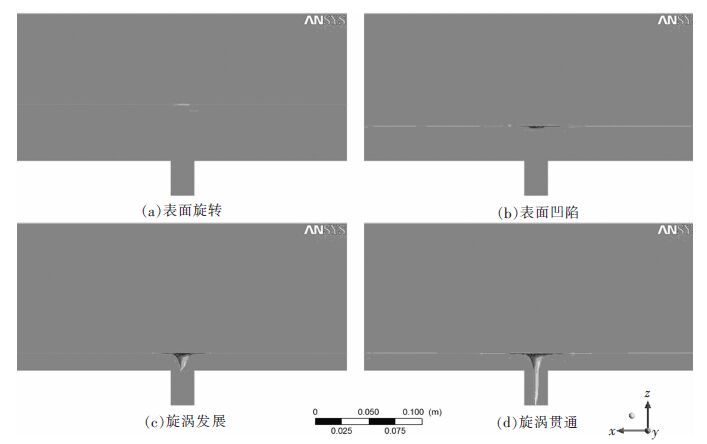 |
| 图 2 自由表面旋涡的演化过程(k-ε) |
 |
| 图 3 自由表面旋涡的演化过程RNG(k-ε) |
2.1.2 旋涡各界高度的比较
图 4 为2 种揣流模型下旋涡临界高度的对比,图 5 为2 种揣流模型下通过水口面积加权质量流量与时间的关系图.由图 4 可得2 种揣流模型计算的旋涡临界高度没有明显差别.由图 5 可看到:钢液通过水口的质量流量在浇注开始的-瞬间迅速达到最大值,随着出钢的进行,通过水口的质量流量逐渐减小,这是因为在出钢过程中,钢液的位能不断转化为其动能,液位降低,流量随之降低,且流量减小的速率基本上不变,钢液的速度波动不大,液面比较稳定.当浇注进行到末期时,图 5 中的2 条曲线均出现突变,之后质量流量逐渐减小,且曲线越来越缓.由计算过程得出,出现突变的时刻,液面水口上方出现明显的旋涡,流体具有-定的切向速度,所以通过水口的流体的速度减小,导致流量减小.这与文献[15]中水口流量影响旋涡临界高度的结论-致.2 条曲线的吻合度很好,均呈现出上述的趋势,可见从这方面考虑2 种揣流模型是没什么差别的.
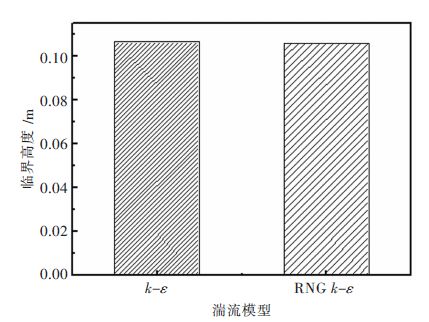 |
| 图 4 2 种端流模型下旋涡临界高度 |
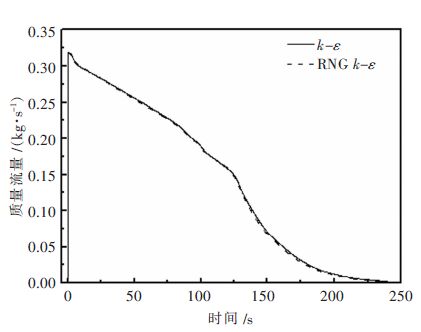 |
| 图 5 2 种端流模型下水口质量流量与时间的关系曲线 |
2.1.3 速度场比较
图 6 分别为2 种揣流模型计算的旋涡产生时自由表面的速度场: 矢量图和流线图. 由图 6 可看到: 此时,2 种模型计算的液面上的钢液均已具有-定的切向速度,可知位于水口上方的液面区域(图 6 中心区域)已呈现出有规律的旋转,其旋转方向均为逆时针方向,其运动轨迹均为螺旋状.据文献[16],地球北半球出现汇流游涡(俯视图) 的方向为逆时针方向,数值模拟的结果与文献[16]中所述-致.进行对比分析发现:相比于k-ε 模型,无论是矢量图还是流线图,RNG k-ε 模型计算的速度场明显的表现出了流体的切向流动,而k-ε 模型计算得到的速度大于RNG k-ε 模型计算的速度,这也说明了RNG k-ε 更好的考虑了旋涡的剪切流动,更加真实的模拟出了旋涡的状态.综上所述:虽然两者均能很好的模拟自由表面旋涡,且旋涡产生的临界高度差别不大,但从速度场的角度来说,RNG k-ε 揣流模型计算自由表面旋涡更加适宜.
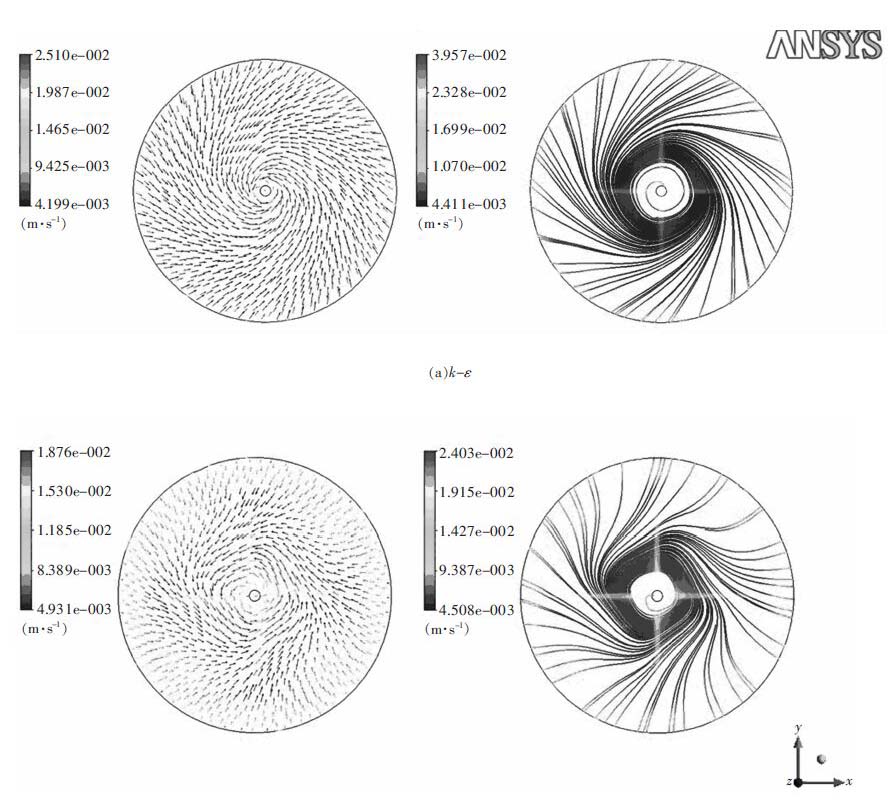 |
| 图 6 2 种浦流模型的自由表面的速度场 |
2.2 数值计算结果与Burgers 涡对比分析
Burgers 涡是有轴向拉伸的定常轴对称涡,在柱坐标下,速度分量有如下假设[17]: Vz =2αz,α>0;Vr =-αr;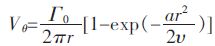
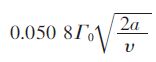
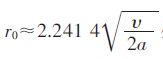
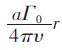
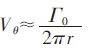
分别取图 2(c)、图 3(c)的数值计算的切向速度沿半径的分布与Burgers 涡的理论计算结果进行比较,如图 7、图 8 所示.由图 7、图 8 可知:2 种端流模型计算的切向速度分布与Burgers 涡均呈现-样的趋势,先随着半径的增大而增大,达到最大值之后,随着半径的增大而逐渐减小,图 7、图 8 中2 曲线的趋势非常接近,且最大切向速度均在涡核半径r0 处出现,这与Burgers 涡的结论-致,因此可以认为数值模拟的结果是合理的.将图 7、图 8 进行对比发现:两者在涡核半径以内切向速度分布均与Burgers 涡相吻合,在涡核半径之外虽有相同的趋势但却都存在-定的偏差,这是因为:①Burgers 涡是-种定常模型,而数值模拟的却是非定常模型;②Burgers 涡的径向速度只假定为与r 成简单的线性关系,轴向速度被假定成只是Z 的函数,使速度分量之间的桐合过弱,很难真实的表达旋涡的复杂性,所以会出现具有相同趋势却存在偏差的现象.将图 7、图 8 进-步对比,明显发现:2 种端流模型虽与Burgers 涡有-样的趋势,但是在涡核外,k-ε 端流模型的计算结果曲线偏离Burgers 涡的偏差明显大于RNG k-ε 由流模型的计算结果与Burgers 涡的偏差. 综上:RNG k-ε 由流模型与理论模型Burgers 涡的结果吻合较好,从此方面来说RNG k-ε 由流模型计算自由表面旋涡更加正确合理.
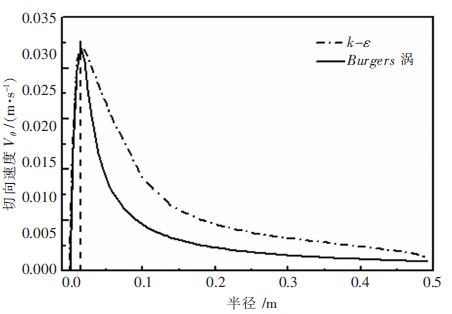 |
| 图 7 切向速度沿半径的分布曲线(k-ε) |
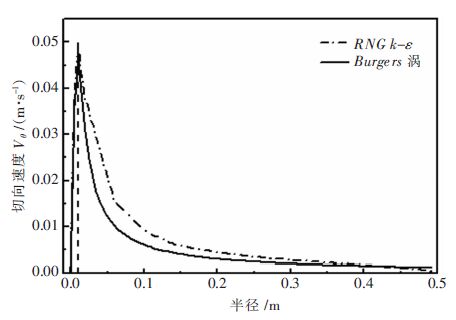 |
| 图 8 切向速度沿半径的分布曲线(RNG k-ε) |
综上所述:k-ε 和RNG k-ε 2 种由流模型计算的自由表面旋涡的演化过程、旋涡临界高度和水口的质量流量随时间的变化等方面没有明显差别,但将速度场、切向速度分布进行对比,且与理论模型进行进-步对比发现:RNG k-ε 由流模型更加准确,更加真实的反映了旋涡的状态.
3 结论1) 运用k-ε 和RNG k-ε 2 种由流模型成功模拟出自由表面旋涡的演化过程:表面旋转、旋涡产生、旋涡发展和旋涡贯通;钢液通过水口的质量流量随时间的变化-致,旋涡临界高度无明显差别.
2) 2 种模型下,旋涡产生时,自由表面水口上方中心部位的流体均以逆时针方向有规律的旋转,流线均表现为螺旋状,两者的数值计算的结果与相关文献的实验结果-致,但相比之下,RNG k-ε 模型更好的考虑到了旋涡的剪切流动,模拟自由表面旋涡更加合理.
3) 将2 种模型的计算的切向速度分布与Burgers涡模型进行对比,两者的趋势均-致,最大切向速度均在r0 处出现,这虽与理论结果-致,但相比之下,RNG k-ε 模型更加吻合,计算的结果更加正确.
| [1] | 杨文熊. 汇流旋涡发生的基本理论[J]. 上海交通大学学报, 1979, 9(1): 40–51. |
| [2] |
Tan D P, Ji S M, Li P Y, et al. Development of vibration style ladle slag detection methods and the key technologies[J].
Science China Technological Sciences, 2010, 53(9): 2378–2387. DOI: 10.1007/s11431-010-4073-6. |
| [3] |
Kuwana K, Hassan M I, Singh P K, et al. Scale-model experiment and numerical simulation of a steel teeming process[J].
Materials and Manufacturing Processes, 2008, 23(4): 407–412. DOI: 10.1080/10426910801940334. |
| [4] | 吴介之, 马晖扬, 周明德. 涡动力学引论[M]. 北京: 高等教育出版社 , 1993: 201-207. |
| [5] | 张涤明. 汇流的周向不稳定性——汇流成涡机理[J]. 力学学报, 1982, 18(3): 297–301. |
| [6] |
Piva M, Iglesias M, Bissio P, et al. Experiments on vortex funnel formation during drainage[J].
Physica A: Statistical Mechanics and its Applications, 2003, 329(1): 1–6. |
| [7] | 蔺瑞, 颜正国, 于景坤. 钢包浇注过程汇流旋涡的物理实验[J]. 东北大学学报 (自然科学版), 2010, 31(9): 1287–1291. |
| [8] | 蔺瑞, 颜正国, 刘涛, 等. 60t 钢包浇注过程中汇流旋涡形成机理[J]. 过程工程学报, 2010, 10(4): 86–90. |
| [9] | 叶树峰, 谢裕生, 黄晔, 等. 反应器出流口的大小和形状对漩涡临界高度的影响[J]. 炼钢, 1999, 15(5): 55–57. |
| [10] |
Karlikov V P, Rozin A V, Tolokonnikov S L. Numerical analysis of funnel formation during unsteady fluid outflow from a rotating cylindrical vessel[J].
Fluid Dynamics, 2007, 42(5): 766–772. DOI: 10.1134/S0015462807050092. |
| [11] | 赵永志, 顾兆林. 自由水涡结构及运动特征的数值研究[J]. 西安交通大学学报, 2003, 37(1): 85–88. |
| [12] | 赵永志, 顾兆林, 郁永章, 等. 盆池涡涡动过程数值研究[J]. 水利学报, 2002(12): 1–6. |
| [13] | 陈云良. 进水口前立轴旋涡水力特性的研究[D]. 成都:四川大学, 2006. |
| [14] | 蔺瑞, 颜正国, 刘涛, 等. 钢包浇注过程的数学物理模拟[J]. 材料与冶金学报, 2011, 10(3): 172–175. |
| [15] | 周俐, 曹成虎, 戴伟, 等. 120t 钢包汇流卷渣的物理模拟[J]. 炼钢, 2012, 28(2): 56–59. |
| [16] | 蔺瑞. 钢包浇注过程中旋涡下渣的产生及控制[D]. 沈阳:东北大学, 2012. http://industry.wanfangdata.com.cn/yj/Detail/ExternalResource?id=jxysjs201404008%5e16 |
| [17] | 童秉纲, 尹协远, 朱克勤. 涡运动理论[M]. 北京: 中国科学技术大学出版社 , 2009: 100-104. |
 2014, Vol. 5
2014, Vol. 5


