2. 中国石油新疆油田公司工程技术研究院, 新疆 克拉玛依 834000;
3. 中国石油川庆钻探钻采工程技术研究院, 四川 成都 610051
2. Engineering Technology Research Institute, Xinjiang Oilfield Company, CNPC, Karamay, Xinjiang 834000, China;
3. CCDC Drilling&Production Engineering Technology Research Institute, Chengdu, Sichuan 610051, China
由于复杂井身结构、复杂井眼轨迹和井径变化导致套管下放困难甚至不能到达预期井深,该类三维复杂井眼套管下放过程中所受摩阻的大小决定了套管是否能够安全有效下放。当套管所受压力载荷超过正弦屈曲和螺旋屈曲临界载荷后,套管发生螺旋屈曲变形,严重螺旋屈曲会使套管与井壁之间的接触力激增,使得套管与井壁之间的摩擦阻力随之增大,当螺旋屈曲套管累积摩阻超过套管重力产生的下放动力后,井口套管大钩载荷无拉力,套管自由稳定停在井中,出现“自锁”现象,此时现场常采用上提冲放作业,几十甚至数百次冲放作业迫使套管下放到预定井深,但也可能导致套管出现断裂失效事故。
对于套管的螺旋屈曲问题,前人做了大量的理论研究和试验分析。Lubinski等[1-2]首次提出了“螺旋屈曲”的概念,并在忽略自重和井壁摩擦力的情况下,利用能量法研究了带封隔器的螺旋屈曲行为,推导出管柱发生螺旋屈曲之后螺距与载荷之间的关系;随后,Paslay等[3-6]推导了套管柱在各井段产生螺旋屈曲时临界载荷的计算公式;Kwon[7]对受自重作用下的管柱螺旋屈曲进行研究并得到螺距的计算公式;高德利等[8]通过现有管柱屈曲理论公式分析管柱螺旋屈曲的临界载荷,研究了套管接头对管柱变形和弯曲应力的影响;Mitchell[9-11]对管柱在水平井眼中的屈曲行为进行更深入的研究,指出管柱发生螺旋屈曲时螺距是不断变化的,并给出了弯曲应力、接触力和摩擦力的计算公式;刘峰等[12]利用有限元方法对水平井眼中钻柱的螺旋屈曲进行分析;高国华等[13-15]对水平井管柱屈曲摩阻计算进行了相关研究。练章华等[16-17]对复杂工况的气井采用ANSYS建立全井筒管柱屈曲行为分析的有限元力学模型,准确描述了油管柱底部非均匀或非完整螺旋屈曲形态;卢玲玲[18]研究了井眼中未封固套管柱正弦屈曲与螺旋屈曲两种失稳变形状态,对比了套管柱正弦屈曲和螺旋屈曲构型沿管柱变化的解析解和数值计算值。秦桦等[19]假设连续管初始形态由正弦屈曲变成螺旋屈曲形态的基础上,推导得到水平井中连续管发生螺旋屈曲的公式。
国内外学者建立了规则井眼套管下放屈曲变形摩阻计算理论公式,但对于复杂井型三维井眼套管屈曲变形,由于接触形态各有差异,不能全面考虑实际工况以及屈曲形态的变化,导致预测结果存在较大误差。因此,针对H井套管下放困难,本文根据实钻井眼轨迹参数和实际套管下放工况建立有限元动力学模型模拟“上提冲放”过程,分析全井段套管受力、套管螺旋屈曲形态及摩阻变化规律。
1 套管柱螺旋屈曲附加摩阻理论 1.1 螺旋屈曲临界载荷计算根据文献[3-7]可得不同井段套管柱螺旋屈曲临界载荷公式,如表 1所示,据此可以判断不同井段套管是否发生螺旋屈曲。当部分井段套管发生螺旋屈曲并与井壁接触时应该考虑由此产生的附加摩阻。
| 表1 不同井段螺旋屈曲临界载荷计算公式 Tab. 1 The formula for calculating critical load of helical buckling in different well segments |
套管下放过程中,下部套管不断累积摩阻成为了上部套管轴向压力,当某部分套管受到轴向压力达到临界载荷时,此段套管将发生螺旋屈曲,严重时会改变套管与井壁的接触状态,与井壁接触产生接触力,从而产生摩阻。因此,在套管发生螺旋屈曲时,套管接触力应考虑附加屈曲接触力,再根据切线方向摩擦系数求出下套管摩擦阻力。
(1) 螺旋屈曲附加接触力
套管下放困难时套管累积摩阻较大,可以认为下部套管承受移动负载或是固定约束,屈曲井段管柱附加接触力
| $ \begin{eqnarray} \left\{ {\begin{array}{*{20}{l}} {Q = \zeta \dfrac{{r{F^2}}}{{EI}}}\\ {{F_{{\rm{hel}}}} = 4\sqrt {EIQ/r} } \end{array}} \right. \end{eqnarray} $ | (1) |
式中:
国内外学者针对不同螺旋屈曲工况,在未考虑管柱自重情况下,式中
(2) 三维复杂井眼管柱接触力
水平井套管下入过程中,三维井眼轨迹上两个测点间的管柱微元段受力如图 1所示,其中假设管柱单元的曲率为常数,管柱轴线与井眼轴线重合,管柱弹性变形且规定轴向力拉正压负。
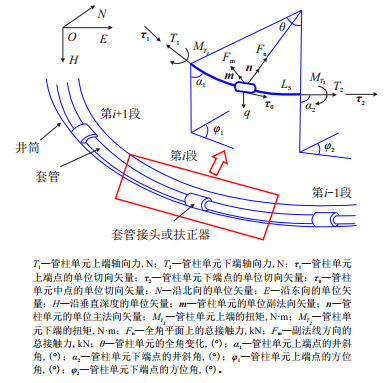 |
| 图1 三维井眼中管柱单元受力示意图 Fig. 1 Force diagram of pipe string element in 3D wellbore |
据此可得管柱单元全角变化
| $ \begin{eqnarray} \left\{ \begin{array}{l} \cos \theta\! = \!\cos {\alpha _1}\cos {\alpha _2}\!+\!\sin {\alpha _1}\sin {\alpha _2}\cos \left( {{\varphi _2}\!-\!{\varphi _1}} \right)\\ \theta = K{L_{\rm{S}}} \end{array} \right. \end{eqnarray} $ | (2) |
式中:
单位长度管柱的有效重力矢量可表示为
| $ \begin{eqnarray} {\boldsymbol{q}} = q{\boldsymbol{k}} \end{eqnarray} $ | (3) |
式中:
全角平面上的总接触力
| $ \begin{eqnarray} {F_{\rm{n}}} = - \left( {{T_1} + {T_2}} \right)\sin \dfrac{\theta }{2} + \pmb{n}{L_{\rm{S}}}q \end{eqnarray} $ | (4) |
副法向方向上的总接触力
| $ \begin{eqnarray} {F_{{\rm{m}}}} = {L_{\rm{S}}}{\pmb{q}} {\pmb{m}} \end{eqnarray} $ | (5) |
| $ \begin{eqnarray} \pmb{m} = \dfrac{{\sin {\alpha _1}\sin {\alpha _2}\sin \left( {{\varphi _2} - {\varphi _1}} \right)}}{{\sin \theta }} \end{eqnarray} $ | (6) |
三维井眼中一个管柱单元的总接触力是全角平面的总接触力和垂直全角平面的总接触力的矢量和,可得单位管长接触力的计算公式
| $ \begin{eqnarray} {F_{\rm{N}}} = \dfrac{{\sqrt {F_{\rm{n}}^2 + F_{\rm{m}}^2} }}{{{L_{\rm{S}}}}} \end{eqnarray} $ | (7) |
(3) 管柱螺旋屈曲摩擦阻力
管柱与井壁间的摩擦系数是影响摩阻的关键因素。摩擦系数的取值要取决于钻井液及泥饼的润滑性能、岩屑性质、接触正压力、滑动状态以及接触面积,通常根据反演或者经验取值。假设摩擦系数为一定值,单元管柱与井壁之间的总摩阻为
| $ \begin{eqnarray} {F_{\rm{t}}} = \mu \left( {{F_{\rm{N}}} + {F_{{\rm{hel}}}}} \right) \end{eqnarray} $ | (8) |
式中:
H井是一口典型复杂井型水平井,实际井深5 876 m,最大井斜角为90.6°,最大狗腿度为7.5°/(30 m),水平位移为2 055 m。该井从3 500 m附近造斜并扭方位,方位角从295°变到110°,水平井A靶井深约4 200 m。二开套管下到3 100 m,三开套管下到5 860 m,裸眼井段长2 760 m。三开下入套管钢级为TP125 V,外径127 mm,壁厚11.1 mm。考虑实钻三维井眼轨迹和井径变化参数,取裸眼段摩擦系数为0.43,上层套管内摩擦系数0.30。
为分析套管下放过程的非线性动力学屈曲形态,建立H井三开套管下放至5 800 m井深时的有限元力学模型,结合现场“上提冲放”作业过程,分析井口套管上提1 100 kN作用力、瞬间释放后自由稳定及下压100 kN作用力3个时刻工况的套管螺旋屈曲行为及摩阻变化。套管与上层套管和裸眼井壁为广义接触,考虑套管浮重、上提冲放动载荷、泥浆阻尼效应、套管屈曲变形。
由此,提取上提1 100 kN、冲放后自由稳定及下压100 kN时刻3种工况所受轴向力及实际井眼轨迹的套管正弦屈曲和螺旋屈曲临界值沿井深分布曲线,如图 2所示。由于实际井眼轨迹和井径变化复杂,直井段套管正弦屈曲和螺旋屈曲临界值很小,在造斜点以下扭方位井段临界值很大且变化剧烈,而水平井段临界值较大且变化比较稳定。
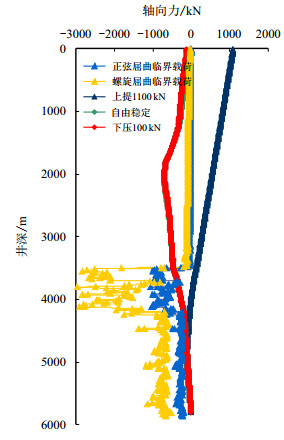 |
| 图2 套管沿井深轴向力及屈曲形态分布图 Fig. 2 Axial force distribution along well depth |
在“上提冲放”作业过程中,当套管“上提”1 100 kN时,直井段套管都承受拉力,套管为拉直状态,但水平井段套管仍保持“上提冲放”之前的接触和变形状态。当“上提冲放”作业瞬间释放井口段套管后弹性变形恢复,被瞬间释放套管会在较快时间内承受惯性冲击力,理论最大瞬间冲击力为1 100 kN,“冲放”驱使套管整体下移。套管释放后,由于阻力和阻尼效应很快恢复为自由稳定工况,套管再次“悬停”在井中,井口套管顶部轴向力为零,全井段套管轴向力转换为压力,部分套管屈曲并与上层套管或裸眼井壁接触,套管总体变形屈曲状态和接触状态发生了根本变化。在“上提冲放”作业过程中,司钻可以利用大钩重量下压井口套管,当井口套管下压100 kN时,井口1 100 m井段套管受到更大轴向压缩力作用,以下井段套管轴向力与自由稳定工况相同,在2 000 m井深附近套管发生了严重螺旋屈曲现象导致此井段套管轴向压力最大。
此外,从图 2可知,3 500 m造斜点以下扭方位井段,所受轴向力逐渐减小直到水平井段套管引鞋端部为零。该动态模拟结果由于考虑了实际工况及螺旋屈曲情况,计算得到套管轴向力在2 000 m井深处最大为
图 3~图 5为上提1 100 kN工况、自由稳定工况以及下压100 kN工况时全井段套管轴向力和法向、切向接触力矢量图。图 6为沿井深取出的全井段套管法向、切向接触力的数值分布。通过对比分析可知,当套管上提1 100 kN时,直井段和弯曲井段套管轴向力为正,承受拉力,套管与井壁的接触点少且接触力小。套管上提释放后恢复自由稳定工况时,全井段套管在重力作用下轴向力为负,直井段套管在2 000 m以下至3 500 m造斜点接触点明显增多,法向接触力大且矢量指向四周,说明发生了严重的三维螺旋屈曲,相应的摩擦力也明显增加。当套管下压100 kN时,仅发现井口以下较短井深的套管轴向力、摩擦力和接触力变化,其余与自由稳定工况受力相似,说明当套管发生螺旋屈曲不能自由下放后,井口下压作业几乎不起作用了。
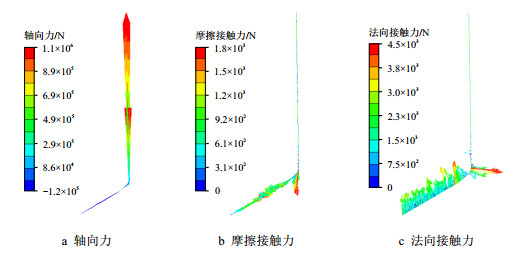 |
| 图3 上提1 100 kN工况全井段套管矢量图 Fig. 3 Vector drawing of whole casing at 1 100 kN condition |
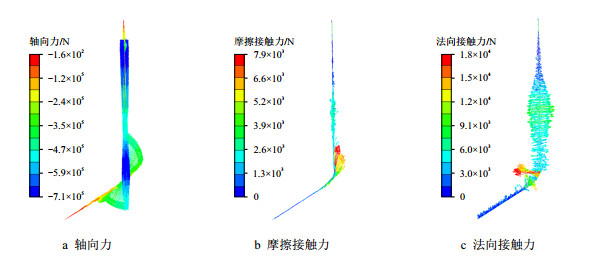 |
| 图4 自由稳定工况全井段套管矢量图 Fig. 4 Vector drawing of whole casing in stable condition |
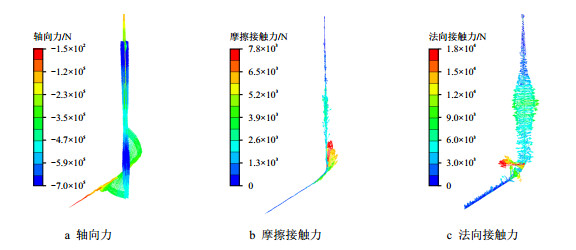 |
| 图5 下压100 kN工况全井段套管矢量图 Fig. 5 Vector diagram of whole casing under 100 kN pressure |
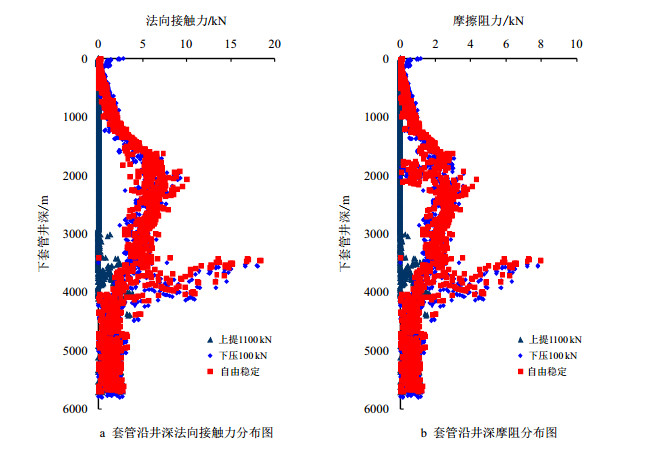 |
| 图6 套管沿井深的摩阻和法向接触力数值分布图 Fig. 6 Casing friction and normal contact force distribution along well depth |
图 7为自由稳定工况时全井段Mises应力分布云图,由图 7可知,套管在井中自由稳定“悬停”时,直井段套管发生了明显屈曲,与图 2临界值井段对应。套管屈曲变形增大了套管弯曲应力,图 7全井段应力云图显示,套管下放过程中本体受到的应力变化不大,且低于套管的屈服强度,表明在“上提下放”作业过程中套管本体的应力在弹性变化范围之内。由于该模型没有考虑螺纹接头,不能排除套管螺纹在严重螺旋屈曲状态下承受巨大弯矩和弯曲应力而出现套管螺纹局部应力进入塑性损伤。可以在该文研究成果基础上进一步开展套管接头螺纹局部应力及损伤分析。
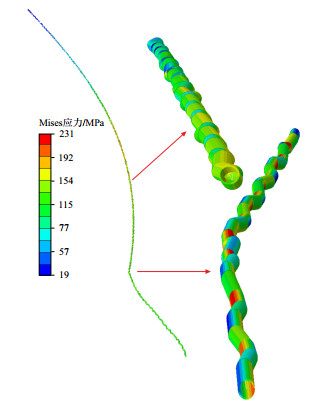 |
| 图7 自由稳定工况全井段套管应力云图 Fig. 7 Stress contour of whole casing in stable condition |
综上可知,H井套管下放困难,表明套管在下放过程中因自重产生的推力小于套管受到的累积摩阻。为此在模拟计算摩阻的基础上从井口向井底累加摩阻,得到3种工况下总累积摩阻分布,如图 8所示。
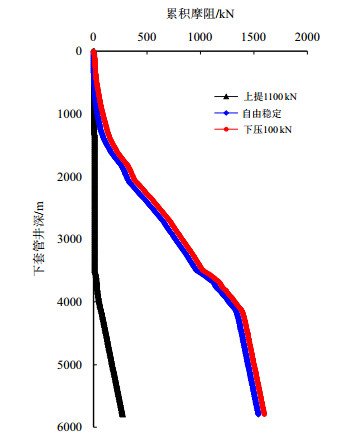 |
| 图8 套管沿井深的累积摩阻分布图 Fig. 8 Cumulative friction distribution along well depth |
上提1 100 kN时,由于受到拉力作用,套管与井壁接触点减少,造斜点以上井段摩阻很小,但水平井段套管由于保持之前的接触和变形状态,此时套管总摩阻约为250 kN。当被释放的套管恢复自由稳定状态时全井段套管摩阻变化较大,直井段套管螺旋屈曲产生了很大摩阻,在1 500 m至4 200 m井段套管总累积摩阻大幅度增加,进入水平井段后以相对较小幅度线性增加,总摩阻约1 550 kN。在井口下压100 kN时,累积摩阻整体变化情况基本与自由稳定状态相似,但由于受到下压作用力,使得累积摩阻值整体略大于自由稳定工况,总摩阻约1 580 kN,说明当直井段套管发生螺旋屈曲导致套管锁死后,继续下压井口套管会进一步增加套管累积摩阻,当累积摩阻大于下放推力后套管不能下放,此时采用下压的方式无法使套管下放至预定井深。
综上所述,H井复杂井眼导致套管在直井段发生了严重的螺旋屈曲,累积摩阻达到最大发生“自锁”,能量无法传递至水平段下部套管,使得套管下放受阻,考虑螺旋屈曲效应的套管模拟结果与实际套管下放工况吻合程度很好,也揭示了该类套管下放困难的根本原因。
3 结论(1)采用理论研究和有限元力学模型分析了三维复杂井眼套管“上提冲放”作业过程,认为考虑了螺旋屈曲附加摩阻将大大增加全井段套管摩阻,计算结果符合实际工况。
(2)研究结果表明三维复杂井眼套管下放时,直井段套管螺旋屈曲产生附加摩阻,套管严重螺旋屈曲导致累积摩阻增大而形成自锁,套管不能下放到位。
(3)建立的模型便于分析现场套管屈曲过程中摩阻、接触力和屈曲形态,明确了套管柱一定井深屈曲变形的状态,为井下套管损伤力学行为研究提供定量的理论依据和方法。
| [1] |
LUBINSKI A, BLENKARN K A. Buckling of tubing in pumping wells, its effects and means for controlling it (includes associated paper 1053-G)[C]. SPE 672-G, 1957. doi: 10.2118/672-G
|
| [2] |
LUBINSKI A, ALTHOUSE W S, LOGAN J L. Helical buckling of tubing sealed in packers[C]. SPE 178-PA, 1962. doi: 10.2118/178-PA
|
| [3] |
PASLAY P R, BOGY D B. The stability of a circular rod laterally constrained to be in contact with an inclined circular cylinder[J]. Journal of Applied Mechanics, 1964, 31(4): 605-610. doi: 10.1115/1.3629721 |
| [4] |
CHEN Y C, LIN Y H, CHEATHAM J B, et al. An analysis of tubing and casing buckling in horizontal wells[C]. OTC 6037-MS, 1989. doi: 10.4043/6037-MS
|
| [5] |
DAWSON R, PASLAY P R. Drill pipe buckling in inclined holes[J]. JPT, 1984, 36(10): 1734-1738. doi: 10.2118/11167-PA |
| [6] |
WU Jiang. Slack-off load transmission in horizontal and inclined wells[C]. SPE 29496-MS, 1995. doi: 10.2118/29496-MS
|
| [7] |
KWON Y W. Analysis of helical buckling[C]. SPE 14729-PA, 1988. doi: 10.2118/14729-PA
|
| [8] |
高德利, 高宝奎. 水平井段管柱屈曲与摩阻分析[J]. 石油大学学报(自然科学版), 2000, 24(2): 1-3. GAO Deli, GAO Baokui. Effects of tubular buckling on torque and drag in horizontal well[J]. Journal of the University of Petroleum, China, 2000, 24(2): 1-3. doi: 10.3321/j.issn:1000-5870.2000.02.001 |
| [9] |
MITCHELL R F. New buckling solutions for extended reach wells[C]. SPE 74566-MS, 2002. doi: 10.-2118/74566-MS
|
| [10] |
MITCHELL R F. Lateral buckling of pipe with connectors in horizontal wells[C]. SPE 59146-MS, 2000. doi: 10.2118/59146-MS
|
| [11] |
MITCHELL R F. Tubing buckling: The state of the art[C]. SPE 104267-MS, 2006. doi: 10.2118/104267-MS
|
| [12] |
刘峰, 王鑫伟. 变曲率井中有重钻柱屈曲的非线性有限元分析[J]. 机械科学与技术, 2007, 26(5): 672-676. LIU Feng, WANG Xinwei. Nonlinear finite element analysis of buckling of drill-tubing with weight in variational curvature wells[J]. Mechanical Science and Technology for Aerospace Engineering, 2007, 26(5): 672-676. doi: 10.3321/j.issn:1003-8728.2007.05.031 |
| [13] |
高国华, 李琪, 李淑芳. 管柱在水平井眼中的屈曲分析[J]. 石油学报, 1996, 17(3): 123-130. GAO Guohua, LI Qi, LI Shufang. A buckling analysis of pipe string in horizontal boreholes[J]. Acta Petrolei Sinica, 1996, 17(3): 123-130. doi: 10.3321/j.issn:0253-2697.1996.03.019 |
| [14] |
刘凤梧, 徐秉业, 高德利. 封隔器对油管螺旋屈曲的影响分析[J]. 清华大学学报(自然科学版), 1999, 39(8): 104-107. LIU Fengwu, XU Bingye, GAO Deli. Packer effect analysis of helical buckling of well tubing[J]. Journal of Tsinghua University (Science and Technology), 1999, 39(8): 104-107. doi: 10.3321/j.issn:1000-0054.1999.08.027 |
| [15] |
嵇国华. 油气井管柱屈曲研究现状与展望[J]. 油气井测试, 2011, 20(2): 16-19. JI Guohua. Well status and prospect of column buckling[J]. Well Testing, 2011, 20(2): 16-19. doi: 10.3969/j.issn.1004-4388.2011.02.005 |
| [16] |
练章华, 牟易升, 刘洋, 等. 高温高压超深气井油管柱屈曲行为研究[J]. 天然气工业, 2018, 38(1): 89-94. LIAN Zhanghua, MOU Yisheng, LIU Yang, et al. Buckling behaviors of tubing strings in HTHP ultra-deep wells[J]. Natural Gas Industry, 2018, 38(1): 89-94. doi: 10.3787/j.issn.1000-0976.2018.01.011 |
| [17] |
练章华, 徐帅, 丁建东, 等. 储气库注采参数与管柱临界屈曲载荷分析[J]. 石油钻采工艺, 2018, 40(1): 131-136. LIAN Zhanghua, XU Shuai, DING Jiandong, et al. Analysis on the injection and production parameters of underground gas storage and the critical buckling load of pipe string[J]. Oil Drilling & Production Technology, 2018, 40(1): 131-136. doi: 10.13639/j.odpt.2018.01.021 |
| [18] |
卢玲玲.未封固套管柱在井眼中的屈曲分析[D].成都: 西南石油大学, 2015. LU Lingling. Buckling analysis of unsealed casing string in borehole[D]. Chengdu: Southwest Petroleum University, 2015. |
| [19] |
秦桦, 安晨, 周传喜, 等. 基于试验的连续管下入特性研究[J]. 石油机械, 2018, 46(9): 7-12. QIN Hua, AN Chen, ZHOU Chuanxi, et al. Research on the behavior of coiled tubing running based on experiment[J]. China Petroleum Machinery, 2018, 46(9): 7-12. doi: 10.16082/j.cnki.issn.1001-4578.2018.09.002 |
| [20] |
高德利. 油气井管柱力学与工程[M]. 北京: 中国石油大学出版社, 2006. GAO Deli. Oil and gas well tubing string mechanics and engineering[M]. Beijing: China University of Petroleum Press, 2006. |
| [21] |
MITCHELL R F. Buckling behavior of well tubing:The packer effect[J]. Society of Petroleum Engineers Journal, 1982, 22(5): 616-624. doi: 10.2118/9264-PA |
| [22] |
CHEN Y C, CHEATHAM J B. Wall contact forces on helically buckled tubulars in inclined wells[J]. Journal of Energy Resources Technology, 1990, 112(2): 142-144. |
| [23] |
张永弘, 刘恩, 何富君, 等. 管柱螺旋屈曲时接触压力的研究[J]. 石油学报, 1998, 19(3): 131-134. ZHANG Yonghong, LIU En, HE Fujun, et al. A study of contact forces on helical buckled tubing in wells[J]. Acta Petrolei Sinica, 1998, 19(3): 131-134. |
 2020, Vol. 42
2020, Vol. 42


