2. 油气藏地质及开发工程国家重点实验室·西南石油大学, 四川 成都 610500
2. State Key Laboratory of Oil&Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu, Sichuan 610500, China
目前,全球油气勘探开发正从浅层向深层、超深层发展,未开发油气资源主要集中在低渗透及深层油气藏等。近年来,中国在深层油气井钻井方面取得了长足的进步,也钻成了一大批深度超过7 000 m的超深井[1-3],其中,亚洲陆上最深井轮探1井目前深度达8 882 m。塔里木盆地顺北油田已经钻成多口井深超过8 000 m的超深小井眼水平井。然而,在超深水平井钻井过程中,钻具刺漏及断裂等钻柱失效事故时有发生。钻柱失效除钻具本身质量因素外,主要原因是钻柱振动导致的钻具疲劳失效。钻柱振动不仅会产生较大的横向位移,使得钻柱的受力和变形更为复杂,而且在瞬态力的作用下还会导致井口钻具安全系数偏低,从而使钻具失效。据顺北油田现场资料分析,有多达15井次超深井在钻井过程中钻具发生断裂,其中两口井顶驱方保处发生断裂。因此,有必要对深井钻柱动力学开展研究并进行钻柱强度校核,以确保钻具的安全性。
自20世纪60年代开始,国内外学者围绕钻柱振动开展了大量研究。Bailey等率先用实验和解析的方法确定了垂直井眼中钻柱振动固有频率的近似值[4];Dareing等考虑钻井液阻尼以及钻头与地层互作用,采用数值分析的方法研究了斜井中钻柱的轴向和扭转振动[5-6];Millheim等考虑钻柱与井壁摩阻、钻头及稳定器的影响,运用有限元法系统分析了BHA动力学特性[7-8];Yigit等建立了纵横扭振动耦合情况下的钻柱动力学模型,仿真结果表明,钻柱运动引起扭转振动,进而引起钻具横向和轴向振动[9-10];Ritto等将钻头与地层互作用考虑为随机接触,建立了钻柱的非线性有限元方程并发展了无参预测的新方法[11-12];Real等在钻头与岩石相互作用模型中考虑了钻头速度与加速度的影响并研究钻柱的扭转动力学[13]。帅健等率先研究井眼弯曲对下部钻具组合振动的影响[14],之后其他学者在钻柱动力学模型中进一步考虑真实井眼轨迹[15]、钻头与地层之间的相互作用[16-17]、钻柱与井壁接触[18-19]、钻井液[20-21]及纵横扭振动耦合[22-24]等因素的影响,完善了钻柱动力学模型,使其应用范围更广,计算结果更精确。
钻柱动力学方面的研究主要是解决水平井井眼轨迹控制和降低钻柱摩阻扭矩,而将钻柱动力学分析结果应用于全井钻柱强度设计,确保钻柱安全方面的应用却很少,在超深水平井钻柱强度校核的应用更是空白。在前期研究的基础上,考虑真实井眼轨迹、钻头与地层互作用、钻柱与井壁接触及钻井液黏滞作用等因素的影响,建立超深井三维井眼全井钻柱动力学模型,并进行钻柱动力学特征仿真模拟,分析钻压及转速对不同井深处钻柱轴向力、扭矩、钻柱位移及等效应力等参数随时间的变化,并根据钻柱动力学模拟结果,对钻具强度和钻具安全性进行评价。
1 钻柱动力学模型 1.1 坐标体系引入大地坐标系
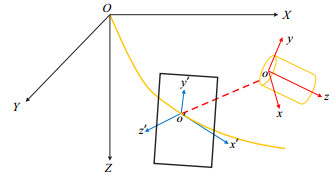 |
| 图1 坐标体系示意图 Fig. 1 The schematic diagram of coordinate systems |
超深水平井的井眼轨迹可以用不同点处的井深、井斜角及方位角表示,根据井深、井斜角及方位角就可以确定三维轨迹的空间形态,而随体坐标系
(1) 井眼为圆形,初始条件下,钻柱轴线与井眼轴线重合,钻头与井壁之间无间隙。
(2) 钻柱可视为匀质弹性梁单元组成,钻柱变形处于线弹性。
(3) 忽略钻柱接头、螺纹及局部孔槽的影响。
(4) 采用库伦摩擦定律描述钻柱与井壁间的摩擦。
(5) 井壁为刚性,与钻柱接触时不发生变形。
1.3 单元动力学模型首先对钻柱进行离散化,将钻柱沿
 |
| 图2 单元受力与变形示意图 Fig. 2 The schematic diagram of unit force and deformation |
单元节点位移矩阵和对应的广义节点力矩阵和考虑梁单元总能量、耗散函数整理得到微元段随体坐标系下的单元运动方程分别为
| $ \begin{eqnarray} {\pmb{U}_{{\rm e}}} = \begin{pmatrix}{{U}_{{ i}}}, \, {{\theta }_{{ yi}}}, \, {{U}_{{ j}}}, \, {{\theta }_{{ yj}}}, \, {{V}_{{i}}}, \, -{{\theta }_{{xi}}}, \, {{V}_{{ j}}}, \, -{{\theta }_{{xj}}}, \, {{W}_{{i}}}, \, {{W}_{{j}}}, \, {{\theta }_{{ zi}}}, \, {{\theta }_{{ zj}}} \end{pmatrix} ^{\rm T} \end{eqnarray} $ | (1) |
| $ \begin{eqnarray} {\pmb{R}_{{\rm e}}} = \left( {{Q}_{{xi}}}, \, {{M}_{{yi}}}, \, {{Q}_{{xj}}}, \, {{M}_{{yj}}}, \, {{Q}_{{yi}}}, \, {{M}_{{xi}}}, \, {{Q}_{{yj}}}, \, {{M}_{{xj}}}, \, {{P}_{{i}}}, \, {{P}_{{ j}}}, \, {{M}_{{zi}}}, \, {{M}_{{zj}}} \right)^{\rm T} \end{eqnarray} $ | (2) |
| $ \begin{eqnarray} {\pmb{M}_{{\rm e}}}{\pmb{\ddot{U}}_{{\rm e}}}+{\pmb{C}_{{\rm e}}}{\pmb{\dot{U}}_{{\rm e}}}+{\pmb{K}_{{\rm e}}}{\pmb{U}_{{\rm e}}} = {\pmb{R}_{{\rm e}}} \end{eqnarray} $ | (3) |
(1) 坐标变换
将大地坐标系绕
| $ \begin{eqnarray} \begin{pmatrix} X \\ Y \\ Z \\ \end{pmatrix} \! = \!\begin{pmatrix}\cos {{\gamma }_{{{Z}^{'}}}} & \cos {{\gamma }_{X}}\sin {{\gamma }_{{{Z}^{'}}}} & \sin {{\gamma }_{X}}\sin {{\gamma }_{{{Z}^{'}}}} \\ -\sin {{\gamma }_{{{Z}^{'}}}} & \cos {{\gamma }_{X}}\cos {{\gamma }_{{{Z}^{'}}}} & \sin {{\gamma }_{X}}\cos {{\gamma }_{{{Z}^{'}}}} \\ 0 & -\sin {{\gamma }_{X}} & \cos {{\gamma }_{X}} \\ \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ \end{pmatrix} \end{eqnarray} $ | (4) |
(2) 全井钻柱动力学模型
坐标转换后,全井钻柱动力学总体运动方程为
| $ \begin{eqnarray} \pmb{ M\ddot{U}}+\pmb{C\dot{U}}+\pmb{KU} = \pmb{R} \end{eqnarray} $ | (5) |
钻柱与井壁接触本质上为随机接触,钻柱与井壁碰撞模型如图 3所示。
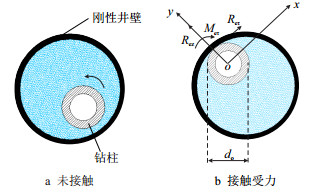 |
| 图3 钻柱与井壁碰撞模型 Fig. 3 Model of the drilling string colliding with the borehole wall |
轴向摩擦阻力
| $ \begin{eqnarray} {{R}_{{\rm ez}}} = {{\mu }_{{\rm z}}}{{R}_{{\rm e }\sigma{\rm }}} \end{eqnarray} $ | (6) |
| $ \begin{eqnarray} {{R}_{{\rm e }\tau{\rm }}} = {{\mu }_{{\rm }\tau{\rm }}}{{R}_{{\rm e }\sigma{\rm }}} \end{eqnarray} $ | (7) |
| $ \begin{eqnarray} {{M}_{{\rm e }\tau{\rm }}} = 0.5{{{d}_{{\rm o}}}}{{R}_{{\rm e }\tau}} \end{eqnarray} $ | (8) |
| $ \begin{eqnarray} {{M}_{{\rm ez}}} = 0.5{{{d}_{{\rm o}}}}{{R}_{{\rm ez}}} \end{eqnarray} $ | (9) |
(1) 上部边界条件
井口钻柱在大钩载荷和转盘驱动下,除沿轴向运动和绕
(2) 下部边界条件
钻头铰支在井底,在钻头处横向位移受到约束,但绕坐标轴方向的转动不约束,此外还受钻头与地层的相互作用产生的激振力
| $ \begin{eqnarray} \left\{ \begin{array}{l} P = {{P}_{{\rm 0}}}\sin \left( \omega t \right) \\ \omega = 19.50{{\left( \dfrac{N}{164} \right)}^{0.65}}{{\left( \dfrac{1750.00}{h} \right)}^{0.65}} \\ {{T}_{{\rm b}}} = \dfrac{1}{3}{{D}_{{\rm b}}}\mu W_{\rm OB} = \\{\kern 40pt}\dfrac{1}{3}{{D}_{{\rm b}}}\mu \big[ {{P}_{{\rm WOB}}}+{{P}_{0}}\sin \left( \omega t \right) \big] \\ \end{array} \right. \end{eqnarray} $ | (10) |
在水平井中,钻柱在上提、下放、旋转钻进过程中受到内压力、外挤压力、轴向力和弯矩的共同作用,有必要对钻柱截面进行等效应力分析。
在水平井中通常按照第四强度理论对钻具进行强度校核,从而确保各种工况下的钻具安全。
钻柱截面的等效应力、钻柱截面弯曲应力、钻井液引起的附加剪应力和扭矩剪应力分别为
| $ \begin{eqnarray} \sigma = \sqrt{{{\left( \left| {{\sigma }_{{\rm p}}} \right|+\left| {{\sigma }_{{\rm w}}} \right| \right)}^{2}}+3\left( \tau _{{\rm n}}^{{\rm 2}}+\tau _{{\rm m}}^{2} \right)} \end{eqnarray} $ | (11) |
| $ \begin{eqnarray} {{\sigma }_{{\rm w}}} = \dfrac{32{{M}_{{\rm w}}}{{d}_{{\rm o}}}}{\pi ( d_{{\rm o}}^{4}-d_{{\rm i}}^{{\rm 4}} )} \end{eqnarray} $ | (12) |
| $ \begin{eqnarray} {{\tau }_{{\rm n}}} = \dfrac{{{A}_{\rm{i}}}\left( {{p}_{{\rm od}}}-{{p}_{{\rm id}}} \right)}{A} \end{eqnarray} $ | (13) |
| $ \begin{eqnarray} {{\tau }_{{\rm m}}} = \dfrac{16T{{d}_{{\rm o}}}}{\pi \left( d_{{\rm o}}^{4}-d_{{\rm i}}^{4} \right)} \end{eqnarray} $ | (14) |
由此,可得钻柱安全系数
| $ \begin{eqnarray} n = \dfrac{{{\sigma }_{{\rm s}}}}{\sigma } \end{eqnarray} $ | (15) |
以塔里木盆地顺北油田某超深水平井为例,该井完钻井深8 225 m,四开水平段钻井液密度1.30 g/cm
| 表1 算例水平井井眼轨迹分段数据 Tab. 1 The wellbore trajectory of a sample horizontal well |
| 表2 算例水平井井身结构 Tab. 2 The casing program of a sample horizontal well |
四开钻具组合:
(1) 钻柱运动状态
模拟了钻压20 kN、转速30 r/min下钻柱的运动状态,图 4为距井口1 000,2 000,3 000和4 000 m处钻柱的运动轨迹。
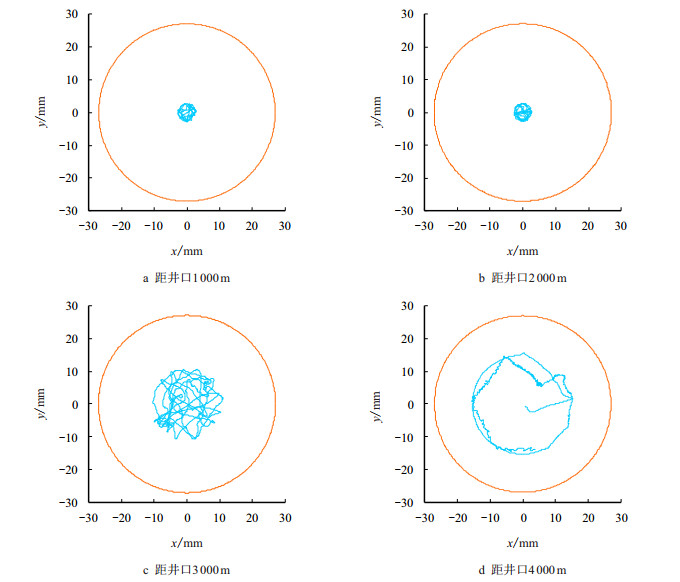 |
| 图4 钻柱横向运动轨迹 Fig. 4 The lateral trajectory of drilling string |
由图 4可见,钻井过程中钻柱的横向运动轨迹较为复杂,呈随机性,钻柱横向位移不大,未发生穿透,离井口越近,钻柱横向运动幅度越小,说明造斜点之上钻柱的横向摆动比井口钻柱的横向摆动大。
(2) 转速对钻柱振动的影响
在小井眼的水平井钻井时,通常转速不是太高;保持钻压20 kN不变,分别模拟转速10,15及30 r/min时钻柱井口轴向力、扭矩、等效应力、安全系数以及MWD(距钻头约15 m)处等效应力及加速度随时间的变化趋势,结果如图 5~图 8所示。
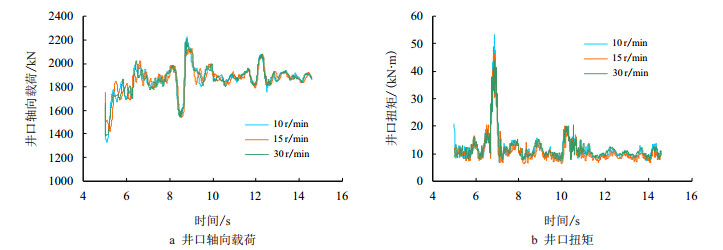 |
| 图5 不同转速下井口轴向载荷及扭矩响应曲线 Fig. 5 Axial load and torque response curve of wellhead at different rotary speeds |
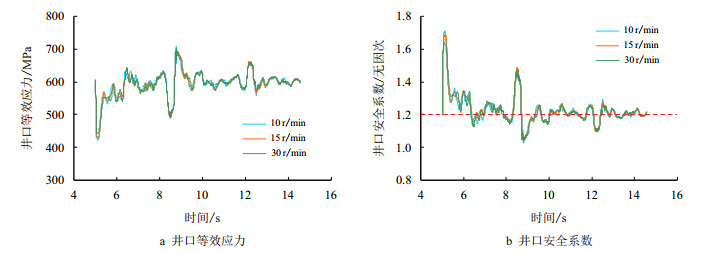 |
| 图6 不同转速下井口等效应力及安全系数响应曲线 Fig. 6 Equivalent stress and safe coefficient response curve of wellhead at different rotary speeds |
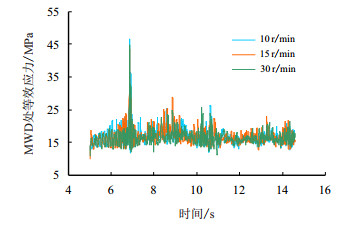 |
| 图7 不同转速下MWD处钻具等效应力响应曲线 Fig. 7 Equivalent stress response curve of MWD at different rotary speeds |
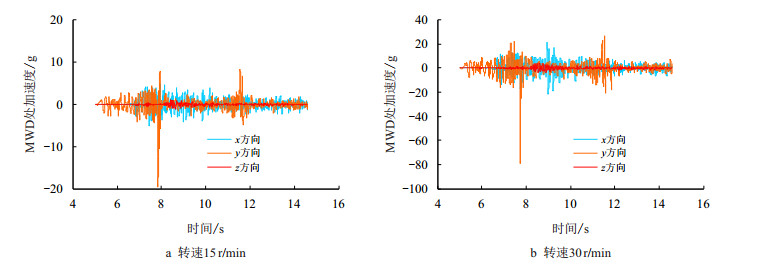 |
| 图8 不同转速下MWD处加速度响应曲线 Fig. 8 Acceleration response curve of MWD at different rotary speeds |
由图 5~图 6可见,井口钻具轴向力及等效应力波动较小,这是因为钻柱长度大,振动阻尼较大,振动传到井口时,高频振动被极大抑制,从而呈现出低频变化的特征。
随着转速的增加,井口轴向力、扭矩、等效应力及安全系数变化不大。在转速变化不大的情况下,转速对井口钻井动力学特征参数的影响不大。井口钻具安全系数在大部分时间内在1.2左右波动,钻具总体而言是安全的,由于安全系数偏低,井口钻具有可能存在钻具失效的安全隐患。由图 7可见,随着转速的增加,MWD处等效应力变化不大,不同转速下,大部分时间段内MWD处等效应力变化幅度为
(3) 钻压对钻柱振动的影响
保持转速10 r/min不变,分别模拟钻压为10和20 kN时钻柱在井口的轴向载荷、扭矩、等效应力、安全系数以及MWD(距钻头约15 m)处加速度及等效应力随时间的变化趋势,模拟结果如图 9~图 12 所示。
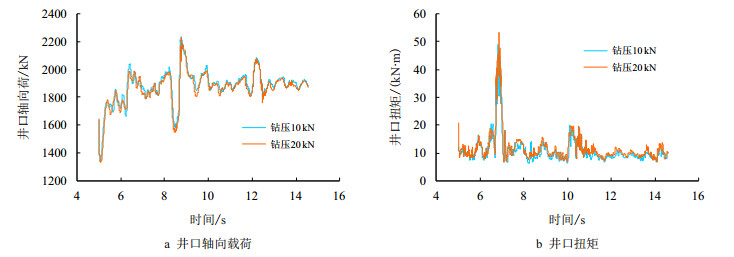 |
| 图9 不同钻压下井口轴向载荷及扭矩响应曲线 Fig. 9 Axial load and torque response curve of wellhead at different WOB's |
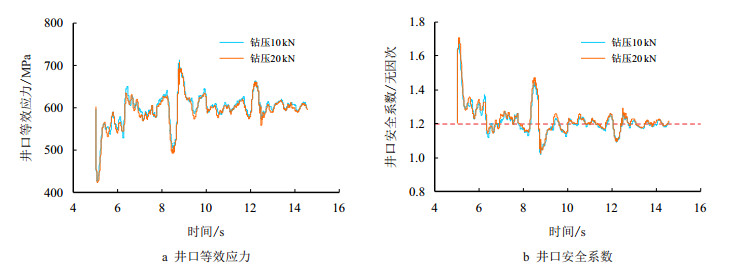 |
| 图10 不同钻压下井口等效应力及安全系数响应曲线 Fig. 10 Equivalent stress and assurance coefficient response curve of wellhead at different WOB's |
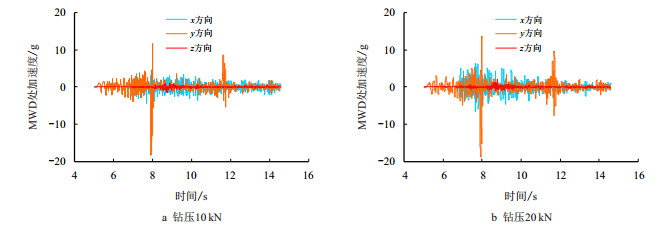 |
| 图11 不同钻压下MWD处加速度响应曲线 Fig. 11 Acceleration response curve of MWD at different WOB's |
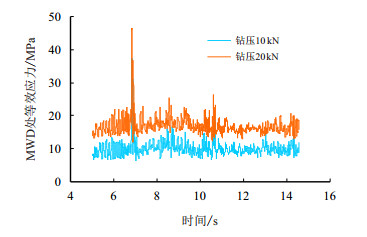 |
| 图12 不同钻压下MWD处钻具等效应力响应曲线 Fig. 12 Equivalent stress response curve of MWD at different WOB's |
由图 9、图 10可见,钻压对井口载荷、扭矩、等效应力及安全系数影响不大,井口载荷及等效应力同样呈低频振动特征。井口安全系数在绝大部分时间在1.2左右波动,钻具总体而言是安全的。
由图 11、图 12可见,MWD处同样呈高频振动特征,等效应力变化幅度为
钻井过程中,钻柱横向运动随机性十分明显。井口附近钻柱横向运动幅度较小,下部钻柱横向运动较为明显;井口轴向力和等效应力表现在一定范围内波动,但波动频率不大;井底钻柱振动较大,特别是MWD处等效应力和加速度表现为高频振动且横向振动比轴向振动更加剧烈。
小井眼超深水平井钻井过程中,现场钻压和转速变化较小,井口轴向载荷、井口扭矩、井口等效应力及井口安全系数随钻压和转速的增加变化不大;MWD处等效应力随钻压增加而增大,随转速增加变化不大;钻压较小时,MWD处加速度随钻压增加变化不大,随转速的增加横向加速度幅值显著增大。
(3) 不同钻压和转速情况下,超深小井眼水平井井口安全系数在大部分时间内在1.2左右波动,钻具总体而言是安全的,由于安全系数偏低,井口钻具在瞬时轴向力和扭矩突变情况下有可能导致钻具失效,需要加强井口钻具的检查和倒换,以保证钻具安全。
符号说明
| [1] |
汪海阁, 葛云华, 石林. 深井超深井钻完井技术现状、挑战和"十三五"发展方向[J]. 天然气工业, 2017, 37(4): 1-8. WANG Haige, GE Yunhua, SHI Lin. Technologies in deep and ultra-deep well drilling:Present status, challenges and future trend in the 13th Five-Year Plan period[J]. Natural Gas Industry, 2017, 37(4): 1-8. doi: 10.3787/j.issn.1000-0976.2017.04.001 |
| [2] |
闫光庆, 张金成. 中国石化超深井钻井技术现状与发展建议[J]. 石油钻探技术, 2013, 41(2): 1-6. YAN Guangqing, ZHANG Jincheng. Status and proposal of the sinopec ultra-deep drilling technology[J]. Petroleum Drilling Techniques, 2013, 41(2): 1-6. doi: 10.3969/j.issn.1001-0890.2013.02.001 |
| [3] |
石林, 汪海阁, 纪国栋. 中石油钻井工程技术现状、挑战及发展趋势[J]. 天然气工业, 2013, 33(10): 1-10. SHI Lin, WANG Haige, JI Guodong. Current situation challenges and developing trend of CNPC's oil & gas drilling[J]. Natural Gas Industry, 2013, 33(10): 1-10. doi: 10.3787/j.issn.1000-0976.2013.10.001 |
| [4] |
BAILEY J J, FINNIE I. An analytical study of drill-string vibration[J]. Journal of Engineering for Industry, 1960, 82(2): 122-127. doi: 10.1115/1.3663017 |
| [5] |
DAREING D W, LIVESAY B J. Longitudinal and angular drill-string vibrations with damping[J]. Journal of Engineering for Industry, 1968, 90(4): 671-679. doi: 10.1115/1.3604707 |
| [6] |
HUANG T, DAREING D W. Buckling and lateral vibration of drill pipe[J]. Journal of Engineering for Industry, 1968, 90(4): 613-619. doi: 10.1115/1.3604697 |
| [7] |
MILLHEIM K K, APOSTAL M C. The effect of bottomhole assembly dynamics on the trajectory of a bit[J]. Journal of Petroleum Technology, 1981, 33(12): 2323-2338. doi: 10.2118/9222-PA |
| [8] |
SPANOS P D, PAYNE M L, SECORA C K. Bottomhole assembly modeling and dynamic response determination[J]. Journal of Energy Resources Technology, 1997, 119(3): 153-158. doi: 10.1115/1.2794983 |
| [9] |
YIGIT A S, CHRISTOFOROU A P. Coupled axial and transverse vibrations of oilwell drillstrings[J]. Journal of Sound and Vibration, 1996, 195(4): 617-627. doi: 10.1006/jsvi.1996.0450 |
| [10] |
CHRISTOFOROU A P, YIGIT A S. Fully coupled vibrations of actively controlled drillstrings[J]. Journal of Sound and Vibration, 2003, 267(5): 1029-1045. doi: 10.1016/S0022-460X(03)00359-6 |
| [11] |
RITTO T G, SOIZE C, SAMPAIO R. Non-linear dynamics of a drill-string with uncertain model of the bit-rock interaction[J]. International Journal of Non-Linear Mechanics, 2009, 44(8): 865-876. doi: 10.1016/j.ijnonlinmec.2009.06.003 |
| [12] |
RITTO T G, ESCALANTE M R, SAMPAIO R. Drill-string horizontal dynamics with uncertainty on the frictional force[J]. Journal of Sound and Vibration, 2013, 332(1): 145-153. doi: 10.1016/j.jsv.2012.08.007 |
| [13] |
REAL F F, BATOU A, RITTO T G. Hysteretic bit/rock interaction model to analyze the torsional dynamics of a drill string[J]. Mechanical Systems and Signal Processing, 2018, 111: 222-233. doi: 10.1016/j.ymssp.2018.04.014 |
| [14] |
帅健, 蔡强康, 吕英民. 弯曲井眼中下部钻具组合的有限元分析[J]. 石油学报, 1990, 11(4): 95-105. SHUAI Jian, CAI Qiangkang, LÜ Yingmin. Finite element analysis of BHA in a curved directional well[J]. Acta Petrolei Sinica, 1990, 11(4): 95-105. doi: 10.3321/j.issn:0253-2697.1990.04.011 |
| [15] |
祝效华, 刘清友, 童华. 三维井眼全井钻柱系统动力学模型研究[J]. 石油学报, 2008, 29(2): 288-291. ZHU Xiaohua, LIU Qingyou, TONG Hua. Research on dynamics model of full hole drilling-string system with three-dimensional trajectory[J]. Acta Petrolei Sinica, 2008, 29(2): 288-291. doi: 10.3321/j.issn:0253-2697.2008.02.025 |
| [16] |
庞东晓, 刘清友, 王国荣, 等. 九自由度牙轮钻头动力学模型研究[J]. 石油学报, 2007, 28(4): 134-137, 141. PANG Dongxiao, LIU Qingyou, WANG Guorong, et al. Dynamic model of roller bit with nine degrees of freedom[J]. Acta Petrolei Sinica, 2007, 28(4): 134-137, 141. doi: 10.3321/j.issn:0253-2697.2007.04.029 |
| [17] |
祝效华, 胡志强. 基于钻头破岩钻进的下部钻具横向振动特性研究[J]. 振动与冲击, 2014, 33(17): 90-93. ZHU Xiaohua, HU Zhiqiang. Lateral vibration characteristics analysis of a bottom hole assembly based on interaction between bit and rock[J]. Journal of Vibration and Shock, 2014, 33(17): 90-93. doi: 10.13465/j.cnki.jvs.2014.17.016 |
| [18] |
程载斌, 姜伟, 任革学, 等. 全井钻柱系统多体动力学模型[J]. 石油学报, 2013, 34(4): 753-758. CHENG Zaibin, JIANG Wei, REN Gexue, et al. A multibody dynamical model of full-hole drillstring system[J]. Acta Petrolei Sinica, 2013, 34(4): 753-758. doi: 10.7623/syxb201304017 |
| [19] |
田家林, 杨应林, 杨琳, 等. 考虑井壁摩擦随机性的钻柱动力学模型[J]. 振动与冲击, 2018, 37(11): 252-258. TIAN Jialin, YANG Yinglin, YANG Lin, et al. Dynamic model of drill strings considering stochastic frictional effects of well wall[J]. Journal of Vibration and Shock, 2018, 37(11): 252-258. doi: 10.13465/j.cnki.jvs.2018.11.036 |
| [20] |
徐鸿志, 路政, 卢晓峰, 等. 钻井液对钻柱振动特性影响分析[J]. 钻井液与完井液, 2010, 27(4): 41-43. XU Hongzhi, LU Zheng, LU Xiaofeng, et al. Effect of drilling fluid on vibrating properties of the drill string[J]. Drilling Fluid & Completion Fluid, 2010, 27(4): 41-43. doi: 10.3969/j.issn.1001-5620.2010.04.014 |
| [21] |
王宝金, 任福深, 朱安贺. 钻井液作用下水平井钻柱横向振动建模与分析[J]. 机械科学与技术, 2018, 37(11): 1670-1677. WANG Baojin, REN Fushen, ZHU Anhe. Modeling and analysis of lateral vibration for horizontal drillstring under action of drilling mud[J]. Mechanical Science and Technology for Aerospace Engineering, 2018, 37(11): 1670-1677. doi: 10.13433/j.cnki.1003-8728.20180077 |
| [22] |
田家林, 吴纯明, 杨勇文, 等. 井下钻柱纵向横向耦合振动模型建立与数值分析[J]. 应用数学和力学, 2017, 38(6): 685-695. TIAN Jialin, WU Chunming, YANG Yongwen, et al. Numerical analysis of downhole drill strings with a longitudinal and lateral coupled vibration model[J]. Applied Mathematics and Mechanics, 2017, 38(6): 685-695. doi: 10.21656/1000-887.370214 |
| [23] |
杨尧焜, 蒋宏伟, 袁志平. 大位移井井下钻柱耦合动力学分析研究[J]. 钻采工艺, 2018, 41(5): 1-4. YANG Yaokun, JIANG Hongwei, YUAN Zhiping. Analysis on downhole tubular coupling dynamics in extended reach drilling[J]. Drilling & Production Technology, 2018, 41(5): 1-4. doi: 10.3969/.j.issn.1006-768X.2018.05.01 |
| [24] |
邹灵战, 毛蕴才, 刘文忠, 等. 盐下复杂压力系统超深井的非常规井身结构设计——以四川盆地五探1井为例[J]. 天然气工业, 2018, 38(7): 73-79. ZOU Lingzhan, MAO Yuncai, LIU Wenzhong, et al. Unconventional casing programs for subsalt ultra-deep wells with a complex pressure system:A case study on Well Wutan 1 in the Sichuan Basin[J]. Natural Gas Industry, 2018, 38(7): 73-79. doi: 10.3787/j.issn.1000-0976.2018.07.010 |
 2020, Vol. 42
2020, Vol. 42


