2. 中国石油新疆油田分公司采油二厂, 新疆 克拉玛依 834000
2. No.2 Oil Production Plant, Xinjiang Oilfield Company, PetroChina, Karamay, Xinjiang 834000, China
CO
从1802年提出的理想气体状态方程至今,状态方程已有长足发展,广泛应用于体系相态计算中。目前,按应用形式和理论基础,现有状态方程可以分为van der Waals(vdW)型及其改进型[8-11]、varial型[12-13]、多参数型[14-16](BWR、BWRS等)以及具有严格统计力学基础的类型(微扰硬链和转子链等)[17-18]。
以上方程虽取得长足发展,但仍然存在不足。(1) vdW型方程对高温高压条件考虑不足,影响实用。(2) varial型方程由于参数过多且不易通过实验获取,只能常用二次或三次截断型,适用范围较低。(3)多参数型方程在非烃气体、重组分及较低温度条件下,计算精度不太令人满意。(4)具有严格统计力学基础的状态方程形式比较复杂,工程应用较少。
CO
PR是应用广泛的vdW型方程之一,能满足vdW型方程所具有的临界点条件,即一种物质在临界点时,临界等温线上的压力对体积的一阶和二阶导数等于零[21-23]。
| $ \left\{ \begin{array}{l} {\left( {\dfrac{{\partial p}}{{\partial v}}} \right)_{{T_{ \rm c }}}} = {\left( {\dfrac{{{\partial ^2}p}}{{\partial {v^2}}}} \right)_{{T_{ \rm c }}}}{ \rm = }0\\[10pt] p = \dfrac{{{ \rm R }T}}{{v - {b_i}}} - \dfrac{{{a_i} \alpha \left( T \right)}}{{v\left( {v + {b_i}} \right) + {b_i}\left( {v - {b_i}} \right)}} \end{array} \right. $ | (1) |
则可以得到式中引力修正系数
| $ \left\{ \begin{array}{l} {a_i} = {\varOmega _{ \rm a }}\dfrac{{{{ \rm R }^2}T_{{ \rm c }i}^2}}{{{p_{{ \rm c }i}}}}\\[10pt] {b_i} = {\varOmega _{ \rm b }}\dfrac{{{ \rm R }{T_{{ \rm c }i}}}}{{{p_{{ \rm c }i}}}} \end{array} \right. $ | (2) |
| $ \alpha \left( T \right) = {\left[ {1 + {m_i}\left( {1 - T_{{ \rm r }i}^{0.5}} \right)} \right]^2} $ | (3) |
| $ {m_i} = 0.37464 + 1.48503{\omega _i} - 0.26992\omega _i^2 $ | (4) |
| $ {\varOmega _{ \rm a }} = 0.45724, {\varOmega _{ \rm b }} = 0.07780 $ | (5) |
PR方程中,无因次系数通过实验回归得到,回归系数应与组分具有相关性而非常数;同时,体积和引力与温度具有较强相关性,无因次系数也应与温度具有较强相关性。因此,对每个组分,将
| $ \begin{eqnarray} \left\{ \begin{array}{l} {\varOmega _{{\rm{a}}{T_{{\rm{r}}i}}}} = f\left( {{T_{{\rm{r}}i}}} \right)\\ {\varOmega _{{\rm{b}}{T_{{\rm{r}}i}}}} = f\left( {{T_{{\rm{r}}i}}} \right) \end{array} \right. \end{eqnarray} $ | (6) |
假设这些与温度有关的参数是对比温度函数的二次方多项式。将式(6)代入式(2),则
| $ \begin{eqnarray} \left\{ \begin{array}{l} {a_i} = {\varOmega _{{\rm{a}}{T_{{\rm{r}}i}}}}\dfrac{{{{\rm{R}}^2}T_{{\rm{c}}i}^2}}{{{p_{{\rm{c}}i}}}}\\[10pt] {b_i} = {\varOmega _{{\rm{b}}{T_{{\rm{r}}i}}}}\dfrac{{{\rm{R}}{T_{{\rm{c}}i}}}}{{{p_{{\rm{c}}i}}}} \end{array} \right. \end{eqnarray} $ | (7) |
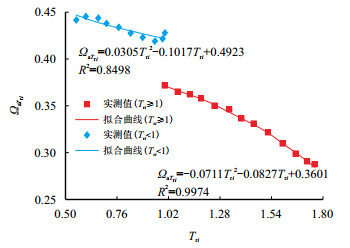
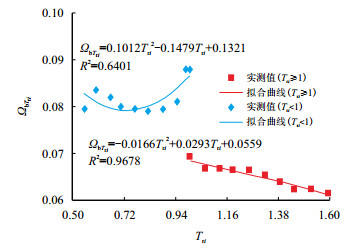
根据实验数据,通过拟合液体密度、饱和蒸汽压的测量值(图 1,图 2),利用二项式回归确定
 |
|
图1
|
 |
|
图2
|
根据对比温度的不同,可以得到
| $ \begin{eqnarray} {\varOmega _{\rm{a}}}_{{T_{{\rm{r}}i}}}\! = \!\left\{ \begin{array}{l} 0.0305T_{{\rm{r}}i}^2\!-\!0.1017{T_{{\rm{r}}i}}\!+\!0.4923, \; \; {{T_{{\rm{r}}i}} < 1} \\ -0.0711T_{{\rm{r}}i}^2\!+\!0.0827{T_{{\rm{r}}i}}\!+\!0.3601, \; \; {{T_{{\rm{r}}i}} \geqslant 1} \end{array} \right. \end{eqnarray} $ | (8) |
根据对比温度的不同,可以得到
| $ \begin{eqnarray} {\varOmega _{\rm{b}}}_{{T_{{\rm{r}}i}}}\! = \!\left\{ \begin{array}{l} 0.1012T_{{\rm{r}}i}^2 - 0.1479{T_{{\rm{r}}i}}\!+\!0.1321, \; \; {{T_{{\rm{r}}i}} < 1} \\[10pt] -0.0166T_{{\rm{r}}i}^2\!+\!0.0293{T_{{\rm{r}}i}}\!+\!0.0559, \; \; {{T_{{\rm{r}}i}} \geqslant 1} \end{array} \right. \end{eqnarray} $ | (9) |
设已知一个由
(1) 平衡气、液相的摩尔分数
| $ \begin{eqnarray} {n_{\rm{V}}} + {n_{\rm{L}}} = 1 \end{eqnarray} $ | (10) |
(2) 平衡气、液相的组成
| $ \begin{eqnarray} \left\{ \begin{array}{l} \sum {{x_i}} = 1\\[8pt] \sum {{y_i}} = 1\\[8pt] \sum {\left( {{y_i} - {x_i}} \right)} = 0 \end{array}\right. \end{eqnarray} $ | (11) |
(3) 平衡气、液相各组分的摩尔质量应满足物质平衡条件
| $ \begin{eqnarray} {y_i}{n_{\rm{V}}} + {x_i}{n_{\rm{L}}} = {z_i} \end{eqnarray} $ | (12) |
(4) 任一组分在平衡气、液相中的分配比例可用平衡常数来描述,即
| $ \begin{eqnarray} {K_i} = {{{y_i}} / {{x_i}}} \end{eqnarray} $ | (13) |
经数学处理,即可得到由平衡气、液相组成方程和物质平衡方程所构成的物质平衡方程
| $ \begin{eqnarray} \sum {\left( {{y_i} - {x_i}} \right)} = {\mbox{$\sum$}} {\dfrac{{{z_i}\left( {{K_i} - 1} \right)}}{{1 + \left( {{K_i} - 1} \right){n_{\rm{V}}}}}} = 0 \end{eqnarray} $ | (14) |
当油气体系达到气液平衡时,体系中各组分在气液相中的逸度应相等[24-25],即
| $ \begin{eqnarray} {y_i}\phi _i^{\rm{V}}p = f_i^{\rm{V}} = f_i^{\rm{L}} = {x_i}\phi _i^{\rm{L}}p \end{eqnarray} $ | (15) |
则,气液平衡常数可以表征为带有逸度的函数
| $ \begin{eqnarray} {K_i} = \dfrac{{{y_i}}}{{{x_i}}} = \dfrac{{\phi _i^{\rm{L}}}}{{\phi _i^{\rm{V}}}} = \dfrac{{{{f_i^{\rm{L}}} / {{x_i}}}}}{{{{f_i^{\rm{V}}} / {{y_i}}}}} \end{eqnarray} $ | (16) |
根据热力学原理求解逸度的严格积分方程为
| $ \begin{eqnarray} \left\{ \begin{array}{l} {\rm{R}}T\ln {\dfrac{{f_i^{\rm{V}}}}{{{y_i}p}}} = {\mbox{$\int$}}_V^\infty {\left[{{{\left( {\dfrac{{\partial p}}{{\partial {n_{{\rm{V}}i}}}}} \right)}_{{v_{\rm{V}}}, \; T, \; {n_{{\rm{V}}j}}}}- \dfrac{{{\rm{R}}T}}{{{v_{\rm{V}}}}}}\right]{\rm{d}}{v_{\rm{V}}}}-{\rm{R}}T\ln {z_{\rm{V}}}\\[15pt] {\rm{R}}T\ln{\dfrac{{f_i^{\rm{L}}}}{{{x_i}p}}} = {\mbox{$\int$}}_L^\infty {\left[{{{\left({\dfrac{{\partial p}}{{\partial {n_{{\rm{L}}i}}}}} \right)}_{{v_{\rm{L}}}, \; T, \; {n_{{\rm{L}}j}}}}- \dfrac{{{\rm{R}}T}}{{{v_{\rm{L}}}}}}\right]{\rm{d}}{v_{\rm{L}}}}-{\rm{R}}T\ln {z_{\rm{L}}} \end{array} \right. \end{eqnarray} $ | (17) |
相态计算的热力学平衡条件目标方程组为
| $ \begin{eqnarray} \left\{ \begin{array}{l} {F_1}\left( {{x_i}, {y_i}, p, T} \right) = f_1^{\rm{L}} - f_1^{\rm{V}} = 0\\[9pt] {F_2}\left( {{x_i}, {y_i}, p, T} \right) = f_2^{\rm{L}} - f_2^{\rm{V}} = 0\\[9pt] \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\[9pt] {F_i}\left( {{x_i}, {y_i}, p, T} \right) = f_i^{\rm{L}} - f_i^{\rm{V}} = 0\\[9pt] \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\[9pt] {F_n}\left( {{x_i}, {y_i}, p, T} \right) = f_n^{\rm{L}} - f_n^{\rm{V}} = 0 \end{array} \right. \end{eqnarray} $ | (18) |
在实际应用过程中,由于研究对象是混合体系,需要引入混合法则对状态方程进行处理[26-28],相应的对常用混合法则修正,分析CO
| $ \begin{eqnarray} \left\{ \begin{array}{l} {a_m} = \sum\limits_i {\sum\limits_j {{y_i}{y_i}{{\left( {{a_i}{a_j}} \right)}^{{1 / 2}}}\left( {1 - {k_{ij}}} \right)} } \\[13pt] {b_m} = \sum\limits_i {\sum\limits_j {{y_i}{y_j}\left[ {{{\left( {{b_i} + {b_j}} \right)} / 2}} \right]\left( {1 - {d_{ij}}} \right)} } \end{array} \right. \end{eqnarray} $ | (19) |
应用室内实验验证修正PR方程的计算结果。利用不同方法计算的密度见表 1,密度计算方法通过状态方程计算出的体积进行转换见式(20),结果表明,采用RK和PR状态方程计算的密度偏低,存在较大误差,本研究建立的方程计算的密度相对误差为0.03%
| 表1 不同压力下各种方法计算密度结果对比 Tab. 1 Comparison of densities at different pressure by different calculation methods |
| 表2 实际油样各种状态方程计算结果对比 Tab. 2 The calculation results of different crude samples by different methods |
图 3
| $ \begin{eqnarray} m = \rho v \end{eqnarray} $ | (20) |
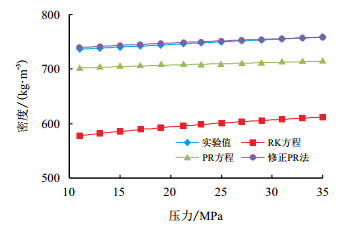 |
| 图3 各种方法计算密度随压力变化曲线 Fig. 3 Curves of densities at different pressures calculated by different methods |
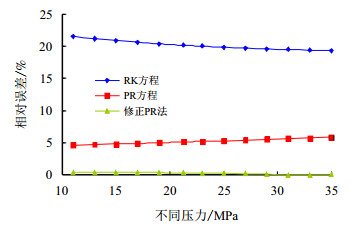 |
| 图4 不同压力下各种方法计算密度相对误差 Fig. 4 Errors of density calculation by different methods at different pressures |
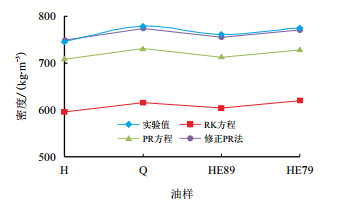 |
| 图5 不同实际油样下各种方法计算密度 Fig. 5 The densities of different crude samples by different methods calculation |
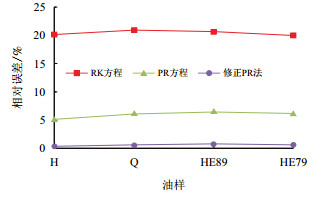 |
| 图6 不同实际油样下各种方法计算密度相对误差 Fig. 6 Errors of densities of different crude samples by different methods calculation |
根据实际油田油样组成(表 3),用不同方法计算的MMP见表 4,结果表明,本研究建立方程计算的密度相对误差是2%
| 表3 油样基本性质参数 Tab. 3 Physical parameters of the crude samples applied in this research |
| 表4 不同方法最小混相压力确定结果对比 Tab. 4 Comparison of the MMP by different methods |
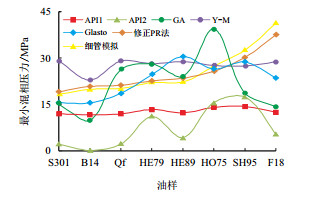 |
| 图7 不同计算方法得到的最小混相压力与实验结果 Fig. 7 Comparison of the calculation MMP by different methods with experimental results |
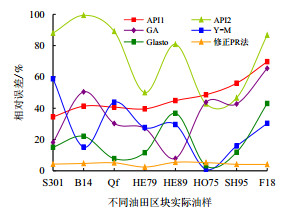 |
| 图8 不同计算方法所得到的最小混相压力计算误差 Fig. 8 Errors of the calculation MMP by different methods |
本文修正的状态方程不仅考虑了温度、压力和混合组分的影响,并且也修正了方程参数,使得非烃类组分也被考虑进来,因而可以获得比较满意的精度。利用本文修正后的状态方程计算所得到的CO
(1) 常用的状态方程中,PR状态方程虽然相对误差20%左右,但由于形式简洁,有较好的应用效果。
(2) 通过对常用的PR状态方程引力项系数(温度系数)和斥力项系数(压力系数)的修正,可以进一步提高其精度,使其工程应用范围进一步扩展,可用于描述CO
(3) 修正后的状态方程对CO
符号说明
R-普适气体常数,R = 8.314 J/(mol
| [1] |
孙志刚, 马炳杰, 李奋. 低渗透储层流体非线性渗流机理及特征分析[J]. 西南石油大学学报(自然科学版), 2019, 41(2): 109-117. SUN Zhigang, MA Bingjie, LI Fen. Mechanism and characteristics of nonlinear flow in porous media of low permeability reservoir[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2019, 41(2): 109-117. doi: 10.11885/j.issn.1674-5086.2018.05.09.02 |
| [2] |
钟太贤, 袁士义, 胡永乐, 等. 凝析气流体的复杂相态[J]. 石油勘探与开发, 2004, 31(2): 125-127. ZHONG Taixian, YUAN Shiyi, HU Yongle, et al. Complex phase behavior of gas condensate systems[J]. Petroleum Exploration and Development, 2004, 31(2): 125-127. doi: 10.3321/j.issn:1000-0747.2004.02.036 |
| [3] |
邸元, 张园, WUYushu. Gibbs自由能最小化法计算二氧化碳-烃-水系统相平衡[J]. 石油学报, 2015, 36(5): 593-599. DI Yuan, ZHANG Yuan, WU Yushu. Phase equilibrium calculation of CO2-hydrocarbons-water system based on Gibbs free energy minimization[J]. Acta Petrolei Sinica, 2015, 36(5): 593-599. doi: 10.7623/syxb201505008 |
| [4] |
刘玉章, 陈兴隆. 低渗油藏CO2驱油混相条件的探讨[J]. 石油勘探与开发, 2010, 37(4): 466-470. LIU Yuzhang, CHEN Xinglong. Miscible conditions of CO2 flooding technology used in low permeability reserviors[J]. Petroleum Exploration and Developmen, 2010, 37(4): 466-470. |
| [5] |
贾凯锋, 王玉霞, 王世璐, 等. 储集层非均质性对低渗透油藏CO2驱油气窜的影响规律[J]. 新疆石油地质, 2019, 40(2): 208-212. JIA Kaifeng, WANG Yuxia, WANG Shilu, et al. Influences of reservoir heterogeneity on gas channeling during CO2 flooding in low permeability reservoirs[J]. Xinjiang Petroleum Geology, 2019, 40(2): 208-212. doi: 10.7657/XJPG20190214 |
| [6] |
雷霄, 代金城, 陈健, 等. 高CO2含量天然气偏差因子影响研究[J]. 西南石油大学学报(自然科学版), 2019, 41(4): 120-126. LEI Xiao, DAI Jincheng, CHEN Jian, et al. Study on influence of high CO2 content on gas deviation factor of natural gas[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2019, 41(4): 120-126. doi: 10.11885/j.issn.1674-5086.2018.06.20.01 |
| [7] |
廉黎明, 秦积舜, 杨思玉, 等. 二氧化碳驱数学模型研究进展及发展方向[J]. 油气地质与采收率, 2013, 20(2): 77-82. LIAN Liming, QIN Jishun, YANG Siyu, et al. Research progress and development directions of mathematical models in CO2 flooding[J]. Petroleum Geology and Recovery Effciency, 2013, 20(2): 77-82. doi: 10.3969/j.issn.1009-9603.2013.02.020 |
| [8] |
PRAUSNITZ J M. Molecular thermodynamics of fluid phase equilibria[M]. Englewood Cliffs: Prentice-Hall, Inc, 1969.
|
| [9] |
REID R C, PRAUSNITZ J M, POLING B E. The properties of gases and liquids[M]. 4th ed. New York: McGrawHill, 1987.
|
| [10] |
REZAEI M, SHADIZADEH S R, VOSOUGHI M, et al. An experimental investigation of sequential CO2 and N2 gas injection as a new EOR method[J]. Energy Sources, Part A:Recovery, Utilization, and Environment Effects, 2014, 36(17): 1938-1948. doi: 10.1080/15567036.2011.557705 |
| [11] |
郭天民, 阎炜, 濮芸辉, 等. 多元气-液平衡和精馏[M]. 北京: 化学工业出版社, 1983. GUO Tianmin, YAN Wei, PU Yunhui, et al. Multi-component gas-liquid equilibrium and distillation[M]. Beijing: Chemical Industry Press, 1983. |
| [12] |
程杰成, 朱维耀, 姜洪福. 特低渗透油藏CO2驱油多相渗流理论模型研究及应用[J]. 石油学报, 2008, 29(2): 246-251. CHENG Jiecheng, ZHU Weiyao, JIANG Hongfu. Study on mathematical models for multi-phase porous flow in CO2 drive of extra-low permeability reservoir and field application[J]. Acta Petrolei Sinica, 2008, 29(2): 246-251. doi: 10.3321/j.issn:0253-2697.2008.02.016 |
| [13] |
李楠, 潘志坚, 苏婷, 等. 超低渗油藏CO2驱正交试验设计与数值模拟优化[J]. 新疆石油地质, 2017, 38(1): 62-65. LI Nan, PAN Zhijian, SU Ting, et al. Orthogonal test design and numerical simulation optimization of CO2 flooding in extra-low permeability reservoirs[J]. Xinjiang Petroleum Geology, 2017, 38(1): 62-65. doi: 10.7657/XJPG20170110 |
| [14] |
ROBERT H, PETR V. The chemical equilibrium of gaseous systms[M]. Boston: Springer Dordrecht, 1976. doi: 10.1007/978-94-010-1775-6
|
| [15] |
廉黎明, 秦积舜, 杨思玉, 等. 用于CO2 -原油体系的改进型黏度预测模型[J]. 石油勘探与开发, 2014, 41(5): 591-596. LIAN Liming, QIN Jishun, YANG Siyu, et al. An improved viscosity model for CO2-crude system[J]. Petroleum Exploration and Developmen, 2014, 41(5): 591-596. doi: 10.11698/PED.2014.05.11 |
| [16] |
沈平平, 黄磊. 二氧化碳原油多相多组分渗流机理研究[J]. 石油学报, 2009, 30(2): 247-251. SHEN Pingping, HUANG Lei. Flow mechanisms of multi-phase multi-component CO2-crude oil system in porous medial[J]. Acta Petrolei Sinica, 2009, 30(2): 247-251. doi: 10.3321/j.issn:0253-2697.2009.02.015 |
| [17] |
王利生, 郭天民. 基于扰动硬链理论的活度系数模型[J]. 石油大学学报(自然科学版), 1995, 19(1): 87-92. WANG Lisheng, GUO Tianmin. An activity coefficient model based on perturbed hard-chain theory[J]. Journal of the University of Petroleum, China, 1995, 19(1): 87-92. |
| [18] |
郭天民. 立方型转子链状态方程及其应用[J]. 化学工程, 1985(1): 1-13, 26. |
| [19] |
王利生, 郭天民. 基于Patel Teja状态方程的统一模型(Ⅱ)——应用于油气藏流体粘度的预测[J]. 化工学报, 1993, 44(6): 685-691. WANG Lisheng, GUO Tianmin. A unified viscosity model based on Patel-Teja equation of state(Ⅱ):Application in predicting viscosities of reservoir fluid[J]. Journal of Chemical Industry and Engineering (China), 1993, 44(6): 685-691. |
| [20] |
郭绪强, 荣淑霞, 杨继涛, 等. 基于PR状态方程的粘度模型[J]. 石油学报, 1999, 20(3): 56-61. GUO Xuqiang, RONG Shuxia, YANG Jitao, et al. The viscosity model based on PR equation of state[J]. Acta Petrolei Sinica, 1999, 20(3): 56-61. |
| [21] |
廉黎明, 秦积舜, 刘同敬, 等. 修正混合规则的BWRS型状态方程及其在CO2原油体系相态计算中的应用[J]. 中国石油大学学报(自然科学版), 2013, 37(2): 81-88. LIAN Liming, QIN Jishun, LIU Tongjing, et al. A BWRS type EOS based on modified mixing-rule and its application in phase behavior of CO2-crude system[J]. Journal of China University of Petroleum, 2013, 37(2): 81-88. doi: 10.3969/j.issn.1673-5005.2013.02.014 |
| [22] |
陈亮, 顾鸿君, 刘荣军, 等. 低渗油藏CO2驱特征曲线理论推导及应用[J]. 新疆石油地质, 2017, 38(2): 229-232. CHEN Liang, GU Hongjun, LIU Rongjun, et al. Derivation and application of CO2 flooding characteristic curves in low permeability reservoirs[J]. Xinjiang Petroleum Geology, 2017, 38(2): 229-232. doi: 10.7657/XJPG20170219 |
| [23] |
郝斐, 程林松, 李春兰, 等. 特低渗透油藏启动压力梯度研究[J]. 西南石油学院学报, 2006, 28(6): 29-32. HAO Fei, CHENG Linsong, LI Chunlan, et al. Study of threshold pressure gradient in ultra-low permeability reservoir[J]. Journal of Southwest Petroleum Institute, 2006, 28(6): 29-32. doi: 10.3863/j.issn.1674-5086.2006.06.008 |
| [24] |
DAUBERT T E, DANNER R P. Phase equilibria in systems containing water[M]. 4th ed. Washington: American Petroleum Institute, 1983.
|
| [25] |
周拓, 刘学伟, 杨正明, 等. 二氧化碳驱储集层堵塞机理实验分析[J]. 石油勘探与开发, 2015, 42(4): 502-506. ZHOU Tuo, LIU Xuewei, YANG Zhengming, et al. Experimental analysis on reservoir blockage mechanism for CO2 flooding[J]. Petroleum Exploration and Development, 2015, 42(4): 502-506. doi: 10.11698/PED.2015.04.12 |
| [26] |
冯高城, 胡云鹏, 姚为英, 等. 注气驱油技术发展应用及海上油田启示[J]. 西南石油大学学报(自然科学版), 2019, 41(1): 147-155. FENG Gaocheng, HU Yunpeng, YAO Weiying, et al. Development and application of gas injection for oil recovery from offshore oilfields[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2019, 41(1): 147-155. doi: 10.11885/j.issn.1674-5086.2018.07.18.01 |
| [27] |
时宇, 杨正明, 黄延章. 低渗透储层非线性渗流模型研究[J]. 石油学报, 2009, 30(5): 731-734. SHI Yu, YANG Zhengming, HUANG Yanzhang. Study on non-linear seepage flow model for low-permeability reservoir[J]. Acta Petrolei Sinica, 2009, 30(5): 731-734. doi: 10.3321/j.issn:0253-2697.2009.05.017 |
| [28] |
郭平, 徐阳, 牛保伦, 等. 胜利油田高89区块低渗油藏CO2近混相驱替机理研究[J]. 特种油气藏, 2012, 19(2): 104-106. GUO Ping, XU Yang, NIU Baolun, et al. The mechanism of quasi-miscible CO2 flooding in Block G89 low permeability reservoir of Shengli Oilfield[J]. Special Oil and Gas Reservoirs, 2012, 19(2): 104-106. doi: 10.3969/j.issn.1006-6535.2012.02.027 |
 2020, Vol. 42
2020, Vol. 42


