南海西部乐东区天然气储量巨大,但储层温度超过195 ℃,压力达100 MPa,渗透率低至0.1 mD,是典型的高温高压低渗气藏,开发难度高,且该区块气井测试回归得到二项式产能方程斜率常为负,无法获取真实产能,严重影响了勘探开发进程。
相对于指数式产能方程,气井二项式产能方程有更加严格的理论做支撑,计算无阻流量可信度更高[1],常规气井产能测试得到的流压和产量通过二项式方程回归后,会得到一条斜率为正的直线[2],外推即求得单井无阻流量。一些学者认为造成高压低渗井二项式产能方程负异常的主要原因是启动压力梯度[3-5]和应力敏感[6-8],一些学者认为是近井带污染[9-10],一些学者认为是井筒产液[11],继而提出高阶二项式方程[12]、三项式方程[13-16]、改进后的一点法[17-19]等修正方法,这些方法均未考虑测试过程中供给范围内的平均地层压力下降带来的误差。高压低渗气井本质上隶属于气井一类,传统二项式方法对个别因素处理过于简化,导致其在回归时易出现异常,本文从地层压力角度分析,考虑有效供给范围内地层压降构建全新二项式方程,不仅适用于高压低渗井,对常规气井的产能分析也更加精确。
1 高压低渗气井二项式产能方程异常原因气井测试过程中,通过不断更改气嘴开度调节产气量,最终测试得到多个不同产量对应的井底流压,进行二项式回归可以得到一条斜率为正的直线
| $ \dfrac{m\left( {{p}_{{\rm R}}} \right)-m\left( {{p}_{{\rm wf}}} \right)}{q}=A+Bq $ | (1) |
| $ m\left( {{p_{\rm{R}}}} \right){\rm{ = 2}}\int_0^{{p_{\rm{R}}}} {\frac{p}{{\mu \left( p \right)Z\left( p \right)}}{\rm{d}}p} $ | (2) |
式中:
LDX-5-A井试井渗透率0.7 mD,测试生产压差较大,见图 1。
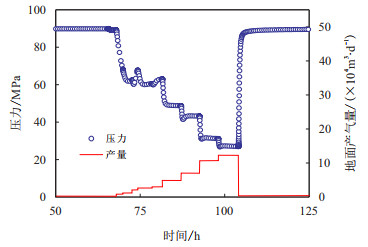 |
| 图1 LDX-5-A井测试情况(截除排液段) Fig. 1 Well LDX-5-A test data(the drainage section removed) |
储层原始地层压力89.87 MPa,5级测试制度产量分别为(2.80,4.82,6.98,10.65,12.25)
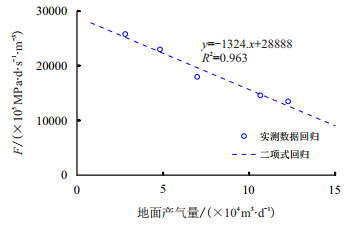 |
| 图2 LDX-5-A井产能二项式回归 Fig. 2 Well LDX-5-A production binomial regression |
高压低渗储层孔隙度较低且压力传播慢,导致有效供给范围小,尽管产量不高但生产压差较大。测试过程中,压降漏斗范围内的平均地层压力下降幅度大。传统二项式回归时,每级均采用原始地层压力,基础数据不准确,导致回归二项式斜率出现负异常。
2 高压低渗气井产能二项式改进 2.1 平均地层压力方程认为测试过程中短时间内压力波无法达到边界,将气藏视为无限大模型,压力波外围即原始地层压力,以井筒为中心的压降漏斗内平均地层压力位于原始地层压力和井底流压之间(图 3,其中,
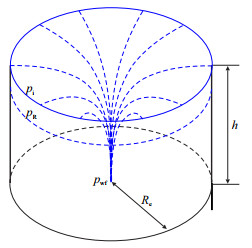 |
| 图3 探井测试过程中平均地层压力示意图 Fig. 3 Schematic diagram of average formation pressure during well testing |
测试过程中,储层遵守物质平衡方程[20]
| $ {{G}_{{\rm p}}}\left( t \right){{B}_{{\rm g}}}\left( t \right)={{G}_{}}\left( t \right){{B}_{{\rm gi}}}\dfrac{{{C}_{{\rm w}}}{{S}_{{\rm wi}}}+{{C}_{{\rm p}}}}{1-{{S}_{{\rm wi}}}}\left[ {{p}_{{\rm i}}}-{{p}_{{\rm R}}}\left( t \right) \right]+ \\{\kern 40pt} {{G}_{}}\left( t \right)\left[ {{B}_{{\rm g}}}\left( t \right)-{{B}_{{\rm gi}}} \right] $ | (3) |
式中:
忽略测试过程中岩石和地层水的体积变化、气体体积系数变化,将式(3)简化为
| $ {{G}_{{\rm p}}}\left( t \right){{B}_{{\rm g}}}={{G}_{}}\left( t \right)\left( {{B}_{{\rm g}}}-{{B}_{{\rm gi}}} \right) $ | (4) |
根据气体状态方程
| $ {{B}_{{\rm g}}}=\dfrac{{{p}_{{\rm sc}}}ZT}{{{p}_{{\rm R}}}{{T}_{{\rm sc}}}} $ | (5) |
| $ {{B}_{{\rm gi}}}=\dfrac{{{p}_{{\rm sc}}}{{Z}_{{\rm i}}}T}{{{p}_{{\rm i}}}{{T}_{{\rm sc}}}} $ | (6) |
式中:
| $ {{R}_{{\rm e}}}\left( t \right)=\sqrt{\dfrac{Kt}{2{\rm{ \mathsf{ π} }} \phi \mu {{C}_{{\rm t}}}}} $ | (7) |
式中:
| $ {{G}_{}}\left( t \right)=\dfrac{\phi {\rm{ \mathsf{ π} }} \left[{{R}_{{\rm e}}}{{\left( t \right)}}\right]^{2}h\left( 1-{{S}_{{\rm w}}} \right)}{{{B}_{{\rm gi}}}} $ | (8) |
其中:
| $ {{G}_{{\rm p}}}\left( t \right)=\sum\limits_{j=1}^{n-1}{{{q}_{j}}{{T}_{j}}}+{{q}_{n}}\left( t-\sum\limits_{j=1}^{n-1}{{{T}_{j}}} \right), {\kern 4pt} 1\leqslant j<n $ | (9) |
式中:
联立式(4)
| $ {{p}_{{\rm R}}\left( t \right)}={{p}_{{\rm i}}}\left[ 1-\dfrac{\sum\limits_{j=1}^{n-1}{{{q}_{j}}{{T}_{j}}}+{{q}_{n}}\left( t-\sum\limits_{j=1}^{n-1}{{{T}_{j}}} \right)}{{\rm{ \mathsf{ π} }} \dfrac{Kt}{{{B}_{{\rm gi}}}\mu {{C}_{{\rm t}}}}h\left( 1-{{S}_{{\rm w}}} \right)} \right] $ | (10) |
以LDX-5-A井为例(各项参数见表 1),根据式(10)计算得到测试期间动用范围内的平均地层压力,见图 4。
| 表1 LDX-5-A井平均地层压力计算参数 Tab. 1 Well LDX-5-A average formation pressure calculation parameters |
 |
| 图4 LDX-5-A井动用范围内的平均地层压力随测试产量和渗透率变化关系 Fig. 4 Average formation pressure in the range of use varies with test yield and permeability of Well LDX-5-A |
除第1级测试外,平均地层压力随产量和时间变化,且每个固定测试制度中平均地层压力变化逐渐缓慢并趋于稳定。随着渗透率逐渐减小平均地层压力下降明显,且下降幅度逐渐增大,表明渗透性越差的储层地层压力下降越大。
2.3 无阻流量求解考虑地层压力变化,提出新的二项式方程回归法
| $ \left\{ \begin{array}{l} m\left( {{p}_{{\rm R1}}} \right)-m\left( {{p}_{{\rm wf1}}} \right)=A{{q}_{{\rm 1}}}+Bq_{{\rm 1}}^{2} \\[5pt] m\left( {{p}_{{\rm R2}}} \right)-m\left( {{p}_{{\rm wf2}}} \right)=A{{q}_{{\rm 2}}}+Bq_{{\rm 2}}^{2} \\[5pt] \vdots \\ m\left( {{p}_{{\rm R}n}} \right)-m\left( {{p}_{{\rm wf}n}} \right)=A{{q}_{n}}+Bq_{n}^{2} \\ \end{array} \right. $ | (11) |
式中:
传统二项式方程回归得到
| $ 2\int_{0.101}^{{p_{\rm{i}}}\left( {1 - C{q_{{\rm{AOF}}}}} \right)} {\frac{p}{{\mu \left( p \right)Z\left( p \right)}}{\rm{d}}p = A{q_{{\rm{AOF}}}} + Bq_{{\rm{AOF}}}^2} $ | (12) |
| $ C=\dfrac{{{B}_{{\rm gi}}}\mu {{C}_{{\rm t}}}}{{\rm{ \mathsf{ π} }} Kh\left( 1-{{S}_{{\rm w}}} \right)} $ | (13) |
式中:
拟压力形式无法求得解析解,需要将方程左边离散处理,采用牛顿-拉普森迭代法求解。若用压力或压力平方形式简化处理可求得解析解
| $ {{q}_{{\rm AOF}}}=\left\{ \begin{array}{l} \dfrac{-{{p}_{{\rm i}}}C-A+\sqrt{{{\left( {{p}_{{\rm i}}}C+A \right)}^{2}}+4B\left( {{p}_{{\rm i}}}-0.101 \right)}}{2B}, {\kern 55pt} \text{压力} \\[8pt] \dfrac{2p_{{\rm i}}^{2}C+A+\sqrt{{{\left( 2p_{{\rm i}}^{2}C+A \right)}^{2}}-4\left( p_{{\rm i}}^{2}{{C}^{2}}-B \right)\left( p_{{\rm i}}^{2}-0.010 \right)}}{2\left( p_{{\rm i}}^{2}{{C}^{2}}-B \right)}, {\kern 10pt} \text{压力平方} \\ \end{array} \right. $ | (14) |
受测试过程中平均地层压力影响,无阻流量不仅与地层原始静压和二项式系数相关,也受到储层物性影响。
3 实例应用采用新方法回归时,考虑不同测试阶段地层压力的变化,以LDX-5-A井为例,新方法回归得到的二项式斜率为正,回归得到
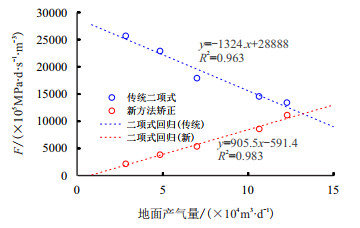 |
| 图5 LDX-5-A井广义产能二项式回归 Fig. 5 Well LDX-5-A generalized production binomial regression |
新方法从气井实际测试过程出发,不仅适用于高压低渗储层,对常规井也能够进行回归并求取无阻流量,且由于考虑了平均地层压力下降,新方法比传统方法计算结果更加准确。
对南海西部油田多口高压低渗气井采用新方法进行二项式回归,斜率均恢复正常,且求得相应无阻流量,此外,对部分常规气井采用新老方法进行对比,见表 2。
| 表2 新老方法无阻流量计算对比 Tab. 2 Calculation of open flow rate of old and new methods |
从表 2中可以看出,常规气井渗透率较高,地层压力下降不明显,故新老方法计算结果较为接近,也证明了新方法的合理性。
4 结论(1) 从物质平衡角度入手,针对气井测试过程中动用范围内的平均地层压力变化构建方程并求解,认为传统方法忽略平均地层压力变化是造成二项式方程斜率为负的主要原因。
(2) 测试过程中,平均地层压力随产量和时间逐渐变化,但在某一特定制度内变化幅度逐渐减小且区域稳定,渗透率对平均地层压力影响较大,渗透性越差的储层地层压力下降越明显。
(3) 新的二项式产能方程,可对南海西部7口高压低渗气井进行回归,得到无阻流量;该方程对4口常规气井回归求得的无阻流量与传统方法所得一致,该方法合理可行。
| [1] |
刘能强. 实用现代试井解释方法[M]. 5版. 北京: 石油工业出版社, 2008. LIU Nengqiang. Practical modern well test interpretation method[M]. 5th Ed. Beijing: Petroleum Industry Press, 2008. |
| [2] |
陈元千. 油气藏工程实践[M]. 北京: 石油工业出版社, 2005. CHEN Yuanqian. Engineering practice of oil and gas reservoirs[M]. Beijing: Petroleum Industry Press, 2005. |
| [3] |
许建红, 程林松, 钱俪丹, 等. 低渗透油藏启动压力梯度新算法及应用[J]. 西南石油大学学报, 2007, 29(4): 64-66. XU Jianhong, CHENG Linsong, QIAN Lidan, et al. A new method and the application on calculating start-up pressure gradient in low permeable reservoirs[J]. Journal of Southwest Petroleum University, 2007, 29(4): 64-66. doi: 10.3863/j.issn.1674-5086.2007.04.015 |
| [4] |
吕成远, 王建, 孙志刚. 低渗透砂岩油藏渗流启动压力梯度实验研究[J]. 石油勘探与开发, 2002, 29(2): 86-89. LÜ Chengyuan, WANG Jian, SUN Zhigang. An experimental study on starting pressure gradient of fluids flow in low permeability sandstone porous media[J]. Petroleum Exploration and Development, 2002, 29(2): 86-89. doi: 10.3321/j.issn:1000-0747.2002.02.023 |
| [5] |
于忠良, 熊伟, 高树生, 等. 致密储层应力敏感性及其对油田开发的影响[J]. 石油学报, 2007, 28(4): 95-98. YU Zhongliang, XIONG Wei, GAO Shusheng, et al. Stress sensitivity of tight reservoir and its influence on oilfield development[J]. Acta Petrolei Sinica, 2007, 28(4): 95-98. doi: 10.3321/j.issn:0253-2697.2007.04.019 |
| [6] |
熊伟, 雷群, 刘先贵, 等. 低渗透油藏拟启动压力梯度[J]. 石油勘探与开发, 2009, 36(2): 232-236. XIONG Wei, LEI Qun, LIU Xiangui, et al. Pseudo threshold pressure gradient to flow for low permeability reservoirs[J]. Petroleum Exploration and Development, 2009, 36(2): 232-236. doi: 10.3321/j.issn:1000-0747.2009.02.015 |
| [7] |
张浩, 康毅力, 陈一健, 等. 致密砂岩油气储层岩石变形理论与应力敏感性[J]. 天然气地球科学, 2004, 15(5): 482-486. ZHANG Hao, KANG Yili, CHEN Yijian, et al. Deformation theory and stress sensitivity of tight sand stones reservoirs[J]. Natural Gas Geoscience, 2004, 15(5): 482-486. doi: 10.3969/j.issn.1672-1926.2004.05.008 |
| [8] |
王宇航, 程时清, 符浩, 等. 考虑应力敏感性的低渗透气藏气井产能分析[J]. 油气井测试, 2017, 26(1): 6-9. WANG Yuhang, CHENG Shiqing, FU Hao, et al. Analysis on gas well productivity of low-permeability gas reservoir with stress-sensitivity[J]. Well Testing, 2017, 26(1): 6-9. doi: 10.3969/j.issn.1004-4388.2017.01.002 |
| [9] |
王洪建, 张义堂, 胡永乐. 伤害表皮变化时气井产能的校正[J]. 石油勘探与开发, 1998(3): 62-65. WANG Hongjian, ZHANG Yitang, HU Yongle. A productivity correction for gas well with changing skin factor[J]. Petroleum Exploration and Development, 1998(3): 62-65. |
| [10] |
袁淋, 李晓平, 赵萍萍, 等. 非均匀污染下水平气井二项式产能公式推导及应用[J]. 特种油气藏, 2013, 20(4): 85-87. YUAN Lin, LI Xiaoping, ZHAO Pingping, et al. Derivation and application of binomial productivity formula for horizontal gas wells under uneven contamination[J]. Special Oil & Gas Reservoirs, 2013, 20(4): 85-87. doi: 10.3969/j.issn.1006-6535.2013.04.021 |
| [11] |
张睿, 孙兵, 秦凌嵩, 等. 气井见水后产能评价研究进展[J]. 断块油气田, 2018, 25(1): 62-65. ZHANG Rui, SUN Bing, QIN Lingsong, et al. Advances in productivity evaluation of water producing gas wells[J]. Fault-Block Oil & Gas Field, 2018, 25(1): 62-65. doi: 10.6056/dkyqt201801013 |
| [12] |
李祖友, 杨筱璧, 罗东明. 高压气井二项式产能方程[J]. 特种油气藏, 2008, 15(3): 62-64. LI Zuyou, YANG Xiaobi, LUO Dongming. Binominal deliverability equation of high pressure gas well[J]. Special Oil & Gas Reservoirs, 2008, 15(3): 62-64. doi: 10.3969/j.issn.1006-6535.2008.03.015 |
| [13] |
李闽, 薛国庆, 罗碧华, 等. 低渗透气藏拟稳态三项式产能方程及应用[J]. 新疆石油地质, 2009, 30(5): 593-595. LI Min, XUE Guoqing, LUO Bihua, et al. Pseudo steadystate trinomial deliverability equation and application of low permeability gas reservoir[J]. Xinjiang Petroleum Geology, 2009, 30(5): 593-595. |
| [14] |
王永胜, 梅海燕, 张茂林, 等. 低渗透水平气井产能分析三项式的推导和应用[J]. 天然气与石油, 2014, 32(6): 53-57. WANG Yongsheng, MEI Haiyan, ZHANG Maolin, et al. Derivation and application of trinomial in low permeability horizontal gas well productivity analysis[J]. Natural Gas and Oil, 2014, 32(6): 53-57. doi: 10.3969/j.issn.1006-5539.2014.06.013 |
| [15] |
梁斌, 张烈辉, 张金庆, 等. 一个新的考虑启动压力梯度的三项式产能方程[J]. 油气井测试, 2012, 21(5): 3-6. LIANG Bin, ZHANG Liehui, ZHANG Jinqing, et al. A novel trinomial deliverability equation with threshold pressure gradient[J]. Well Testing, 2012, 21(5): 3-6. doi: 10.3969/j.issn.1004-4388.2012.05.003 |
| [16] |
孟琦, 刘红兵, 万鹤, 等. 低渗透气藏气井产能预测新方法[J]. 非常规油气, 2018, 5(2): 50-54. MENG Qi, LIU Hongbing, WAN He, et al. A new method for production of gas wells in low permeability reservoirs[J]. Unconventonal Oil & Gas, 2018, 5(2): 50-54. doi: 10.3969/j.issn.2095-8471.2018.02.008 |
| [17] |
石军太, 李骞, 张磊, 等. 多层合采气井产能指示曲线异常的原因与校正方法[J]. 天然气工业, 2018, 38(3): 50-59. SHI Juntai, LI Qian, ZHANG Lei, et al. An abnormality of productivity indicative curves for multi-layer gas wells:Reason analysis and a correction method[J]. Natural Gas Industry, 2018, 38(3): 50-59. doi: 10.3787/j.issn.1000-0976.2018.03.006 |
| [18] |
马时刚, 沈文杰. 海上异常高压气藏产能计算研究——以锦州M气田为例[J]. 油气井测试, 2015, 24(4): 32-34. MA Shigang, SHEN Wenjie. The productivity calculation of abnormal high pressure gas reservoirs:Taking Jinzhou M Gas Field as example[J]. Well Testing, 2015, 24(4): 32-34. doi: 10.3969/j.issn.1004-4388.2015.04.009 |
| [19] |
马时刚, 李波, 王世民, 等. 一点法在锦州20-2凝析气田的应用与改进[J]. 天然气勘探与开发, 2008, 31(1): 17-19. MA Shigang, LI Bo, WANG Shimin, et al. Application and improvement of one empirical equation on Jinzhou20-2 Condensate Field[J]. Well Testing, 2008, 31(1): 17-19. doi: 10.3969/j.issn.1004-4388.2008.03.007 |
| [20] |
黄炳光, 冉新权, 李晓平. 气藏工程分析方法[M]. 北京: 石油工业出版社, 2004. HUANG Bingguang, RAN Xinquan, LI Xiaoping. Gas reservoir engineering analysis[M]. Beijing: Petroleum Industry Press, 2004. |
 2020, Vol. 42
2020, Vol. 42


