2. 中国石油西南油气田分公司川西北气矿, 四川 江油 621700
2. Sichuan Northwest Gas Mine of Southwest Oil and Gas Field Branch, PetroChina, Jiangyou, Sichuan 621700, China
裂缝性气藏储层多为致密储层,裂缝是该类储层中重要的气体储存空间与传输通道。裂缝系统形态与体积决定了裂缝性气藏气井的产能与稳产能力[1]。对于该类型气藏的试井模型研究方法主要分为4类:第1类研究方法为使用连续双重介质描述裂缝性气藏非均质储层,结合渗流力学理论,建立裂缝性气藏试井模型,模拟气体在裂缝性油气藏内的流动,该类方法无法描述裂缝系统形态与试井压力动态曲线的关系[2-4];第2类研究方法是基于数值试井理论方法,利用离散裂缝网络(DFN)描述裂缝性油气藏的大尺度裂缝,模拟其试井时的压力变化规律,该类方法的缺点在于仅能模拟大尺度裂缝,受限于计算机处理能力与内存限制,无法描述小尺寸分支裂缝及其形成的网络系统[5-7];第3类研究方法是使用分形连续双重介质描述不同尺度下储层的非均质性,该类方法同样存在裂缝形态描述上的问题[8-10];第4类方法使用分形参数控制不同长度的裂缝,形成平行或相交网络,嵌入储层基质中,形成具有多尺度分形性质的天然裂缝性油气藏模型[11-13],该方法能够很好地表征裂缝网络的形态与分布,但该类裂缝网络以直线和相交的直线为主,并不能完全模拟趋向井底的径向流动[14-15]。
本文利用树状分形网络对趋向井底的径向流动模拟的优越性,使用树状分形网络模拟气藏裂缝系统,并将树状分形网络嵌入到基质中,提出基于树状分形网络的裂缝性气藏试井模型,分析基于树状分形网络的裂缝性气藏压力动态特征的影响因素,为裂缝性气藏的动态描述及试井分析提供了一种新方法。
1 物理模型树状分形网络由一系列分叉结构组合而成,考虑到网络的对称性,可以在计算时只分析网络的一个单元,如图 1所示。生成网络之前,需要生成多个不同级(总分叉级数
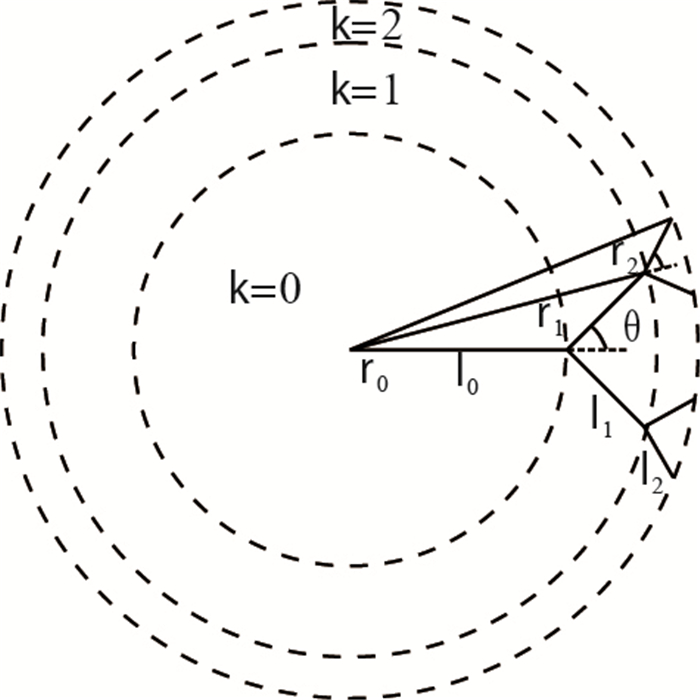 |
| 图1 基于树状分形网络的裂缝性气藏模型 Fig. 1 Fractured gas reservoir model based on tree fractal network |
本文研究的是裂缝性气藏圆形地层,井位于圆心
气藏储层由多个不同级(总分叉级数
| $ {{l}_{k}}={{\alpha }^{k}}{{l}_{0}} $ | (1) |
式中:
单条
| $ {{d}_{k}}={{\beta }^{k}}{{d}_{0}} $ | (2) |
式中:
径向距离为井到各区域界面的距离,由式(1),可得
| $ {{r}_{k}}=\sum\limits_{i=0}^{k}{{{l}_{i}}\cos \theta }={{l}_{0}}\left[1+\dfrac{\alpha \left( 1-{{\alpha }^{k}} \right)\cos \theta }{1-\alpha } \right] $ | (3) |
式中:
Xu等将单条
| $ {{K}_{k}}=10^{-12}\dfrac{d_{k}^{2}}{32}\dfrac{1}{{{T}_{k}}} $ | (4) |
式中:
区域
| $ {{T}_{k}}=\dfrac{{{l}_{k}}}{{{r}_{k}}-{{r}_{k-1}}}=\left\{ \begin{array}{*{35}{l}}1, {\kern 32pt} k=0 \\ \sec \theta, {\kern 18pt} k>0 \\\end{array} \right. $ | (5) |
联立式(2)~式(5),得到区域
| $ {{K}_{{\rm f}k}}=\left\{ \begin{array}{*{35}{l}}\dfrac{10^{-12}Nd_{0}^{2}}{32}, {\kern 52pt} k=0 \\[8pt] \dfrac{10^{-12}N{{n}^{k}}{{\beta }^{2k}}d_{0}^{2}\cos \theta }{32}, {\kern 10pt} k>0 \\\end{array} \right. $ | (6) |
式中:
区域
| $ {{V}_{{\rm t}k}}=\left\{ \begin{array}{*{35}{l}} \pi hr_{0}^{2}, {\kern 48pt} k=0 \\ \pi h\left( r_{k}^{2}-r_{k-1}^{2} \right), {\kern 10pt} k>0 \\ \end{array} \right. $ | (7) |
式中:
区域
| $ {{V}_{{\rm ft}k}}=N{{n}^{k}}\dfrac{\pi {{l}_{k}}d_{k}^{2}}{4}=\dfrac{N\pi {{n}^{k}}{{\alpha }^{k}}{{\beta }^{2k}}{{l}_{0}}d_{0}^{2}}{4} $ | (8) |
式中:
区域
| $ {{V}_{{\rm mt}k}}={{\phi }_{{\rm mp}}}\left( {{V}_{{\rm t}k}}-{{V}_{{\rm tf}k}} \right) $ | (9) |
式中:
联立式(7)、式(8),区域
| $ {{\phi }_{{\rm f}k}}=\dfrac{{{V}_{{\rm ft}k}}}{{{V}_{{\rm t}k}}}=\left\{ \begin{array}{*{35}{l}}\dfrac{Nd_{0}^{2}}{4h{{l}_{0}}}, {\kern 65pt} k=0 \\[6pt] \dfrac{N{{n}^{k}}{{\alpha }^{k}}{{\beta }^{2k}}{{l}_{0}}d_{0}^{2}}{4h\left( r_{k}^{2}-r_{k-1}^{2} \right)} k=0, {\kern 5pt} k>0 \\\end{array} \right. $ | (10) |
式中:
联立式(7)~式(10),区域
| $ {{\phi }_{{\rm m}k}}=\dfrac{{{V}_{{\rm mt}k}}}{{{V}_{{\rm t}k}}}={{\phi }_{{\rm mp}}}\left( 1-{{\phi }_{{\rm f}k}} \right) $ | (11) |
式中:
在双分叉结构下,裂缝性气藏各区域裂缝系统渗透率、裂缝体积相等的条件为
当
| $ \left\{ \begin{array}{*{35}{l}} {{K}_{{\rm f}k}}\left( \dfrac{{{\partial }^{2}}{{\psi }_{{\rm f}k}}}{\partial {{r}^{2}}}+\dfrac{1}{r}\dfrac{\partial {{\psi }_{{\rm f}k}}}{\partial r} \right)+a{{K}_{{\rm m}}}\left( {{\psi }_{{\rm m}k}}-{{\psi }_{{\rm f}k}} \right)= \dfrac{\mu {{\phi }_{{\rm f}k}}{{C}_{{\rm tf}}}}{3.6}\dfrac{\partial {{\psi }_{{\rm f}k}}}{\partial t}, {\kern 28pt} \\ {{r}_{k-1}}\leqslant r \leqslant {{r}_{k}} \\ -a{{K}_{{\rm m}}}\left( {{\psi }_{{\rm m}k}}-{{\psi }_{{\rm f}k}} \right)=\dfrac{\mu {{\phi }_{{\rm m}k}}{{C}_{{\rm tm}}}}{3.6}\dfrac{\partial {{\psi }_{{\rm m}k}}}{\partial t}, {\kern 112pt} \\ {{r}_{k-1}}\leqslant r\leqslant {{r}_{k}} \\ {{\psi }_{{\rm f}k}}(r, 0)={{\psi }_{{\rm m}k}}(r, 0)={{\psi }_{{\rm i}}}, {\kern 158pt} \\ k=0, 1, \cdots, M \\ {{\left. \left( r\dfrac{\partial {{\psi }_{{\rm f}k}}}{\partial r} \right) \right|}_{{{r}_{{\rm e}}}={{r}_{{\rm w}}, k =1}}}{\rm =}-\left( 1-C\dfrac{{\rm d}{{\psi }_{{\rm wf}}}}{{\rm d}t} \right), {\kern 120pt} \\ {{\psi }_{{\rm wf}}}={{\left. {{\psi }_{{\rm f}k}} \right|}_{k=1, r={{r}_{{\rm w}}}{{{\rm e}}^{-S}}}} \\ {{\left. {{\psi }_{{\rm f}k}} \right|}_{r={{r}_{k}}}}={{\left. {{\psi }_{{\rm f}\left( k+1 \right)}} \right|}_{r={{r}_{k}}}}, {\kern 175pt} \\ k=0, 1, \cdots, M-1 \\[6pt] {{\left. \dfrac{\partial {{\psi }_{{\rm f}k}}}{\partial r} \right|}_{r={{r}_{k}}}}={{\left. \dfrac{{{K}_{{\rm f}\left( k+1 \right)}}}{{{K}_{{\rm f}k}}}\dfrac{\partial {{\psi }_{{\rm f}\left( k+1 \right)}}}{\partial r} \right|}_{r={{r}_{k}}}}, {\kern 131pt} \\ k=0, 1, \cdots, M-1 \\ {{\psi }_{{\rm f}k}}\left( t \right)={{\psi }_{{\rm i}}}, {\kern 217pt} \\ r\to \infty, k= M \\ \end{array} \right. $ | (12) |
式中:
裂缝系统和基质系统的拟压力可以分别表示为
| $ {\psi _{{\text{f}}k}} = \int_{{p_0}}^{{p_{{\text{f}}k}}} {\frac{{2p}}{{\mu Z}}{\text{d}}p}, \;\;\;\;\;\;{r_{k-1}} \leqslant r \leqslant {r_k} $ | (13) |
| $ {\psi _{{\text{m}}k}} = \int_{{p_0}}^{{p_{{\text{m}}k}}} {\frac{{2p}}{{\mu Z}}{\text{d}}p}, \;\;\;\;\;\;{r_{k-1}} \leqslant r \leqslant {r_k} $ | (14) |
式中:
为简化数学模型及求解方便,定义下列无因次变量[21]。
区域
| $ {{\psi }_{{\rm Df}k}}=\dfrac{78.489{{K}_{{\rm f}k}}h}{T{{q}_{{\rm sc}}}}\left( {{\psi }_{{\rm i}}}-{{\psi }_{{\rm f}k}} \right) $ | (15) |
式中:
区域
| $ {{\psi }_{{\rm Dm}k}}=\dfrac{78.489{{K}_{{\rm m}k}}h}{T{{q}_{{\rm sc}}}}\left( {{\psi }_{{\rm i}}}-{{\psi }_{{\rm m}k}} \right) $ | (16) |
式中:
无因次有效半径为
| $ {{r}_{{\rm De}}}=\dfrac{r}{{{r}_{{\rm w}}}}{{{\rm e}}^{S}} $ | (17) |
式中:
无因次有效界面半径为
| $ {{r}_{{\rm De}k}}=\dfrac{{{r}_{k}}}{{{r}_{{\rm w}}}}{{{\rm e}}^{S}} $ | (18) |
式中:
无因次有效时间为
| $ {{t}_{{\rm De}}}={\dfrac{{3.6{K_{{\rm{f}}0}}t{{\rm{e}}^{2S}}}}{{{\phi _{{\rm{fm0}}}}{C_{{\rm{tfm0}}}}\mu r_{\rm{w}}^2}}} $ | (19) |
式中:
无因次有效井筒储积系数为
| $ {{C}_{{\rm De}}}=\dfrac{C{{{\rm e}}^{2S}}}{2\pi h{\phi _{{\rm{fm0}}}}{C_{{\rm{tfm0}}}}r_{{\rm w}}^{2}} $ | (20) |
式中:
区域
| $ {{\omega }_{k}}=\dfrac{{{\phi }_{{\rm f}k}}{{C}_{{\rm ft}}}}{{{\phi }_{{\rm m}k}}{{C}_{{\rm tm}}}+{{\phi }_{{\rm f}k}}{{C}_{{\rm ft}}}} $ | (21) |
式中:
区域
| $ {{\lambda }_{k}}=a\dfrac{{{K}_{\rm m}}}{{{K}_{{\rm f}k}}}r_{\rm w}^{2} $ | (22) |
式中:
无因次的渗流数学模型为
| $ \left\{ \begin{array}{*{35}{l}} \dfrac{{{\partial }^{2}}{{\psi }_{{\rm Df}k}}}{\partial r_{{\rm De}}^{2}}+\dfrac{1}{{{r}_{{\rm De}}}}\dfrac{\partial {{\psi }_{{\rm Df}k}}}{\partial {{r}_{{\rm De}}}}+{{\lambda }_{k}}{{{\rm e}}^{-2S}}\left( \dfrac{{{K}_{{\rm f}k}}}{{{K}_{{\rm m}}}}{{\psi }_{{\rm Dm}k}}-{{\psi }_{{\rm Df}k}} \right)=\\ \dfrac{{{\omega }_{k}}}{{{C}_{{\rm De}}}}\dfrac{{{K}_{{\rm f}0}}}{{{K}_{{\rm f}k}}}\dfrac{\partial {{\psi }_{{\rm Df}k}}}{\partial \left( {{{t}_{{\rm De}}}}/{{{C}_{{\rm De}}}}\; \right)}, {\kern 10pt} {{r}_{{\rm De}\left( k-1 \right)}}\leqslant {{r}_{{\rm De}}}\leqslant {{r}_{{\rm De}k}} \\ -{{\lambda }_{k}}{{{\rm e}}^{-2S}}\left( {{\psi }_{{\rm Dm}k}}-\dfrac{{{K}_{{\rm m}}}}{{{K}_{{\rm f}k}}}{{\psi }_{{\rm Df}k}} \right)=\dfrac{{\rm 1}-{{\omega }_{k}}}{{{C}_{{\rm De}}}}\dfrac{{{K}_{{\rm f}0}}}{{{K}_{{\rm f}k}}}\dfrac{\partial {{\psi }_{{\rm Dm}k}}}{\partial \left( {{{t}_{{\rm De}}}}/{{{C}_{{\rm De}}}}\; \right)}, {\kern 86pt} \\ {{r}_{{\rm De}\left( k-1 \right)}}\leqslant {{r}_{{\rm De}}}\leqslant {{r}_{{\rm De}k}} \\ {{\psi }_{{\rm Df}k}}({{r}_{{\rm De}}}, 0)={{\psi }_{{\rm Dm}k}}({{r}_{{\rm De}}}, 0)=0, {\kern 178pt}\\ k=0, 1, \cdots, M \\ \dfrac{{\rm d}{{\psi }_{{\rm wD}}}}{{\rm d}\left( {{{t}_{{\rm De}}}}/{{{C}_{{\rm De}}}}\; \right)}-{{\left. \left( {{r}_{{\rm De}}}\dfrac{\partial {{\psi }_{{\rm Df}0}}}{\partial {{r}_{{\rm De}}}} \right) \right|}_{{{r}_{{\rm De}}}=1}}=1, {\kern 156pt} \\ {{\psi }_{{\rm wD}}}={{\left. {{\psi }_{{\rm Df0}}} \right|}_{{{r}_{{\rm De}}}=1}} \\[6pt] {{\left. {{\psi }_{{\rm Df}k}} \right|}_{{{r}_{{\rm De}}}={{r}_{{\rm De}k}}}}={{\left. {{\psi }_{{\rm Df}\left( k+1 \right)}} \right|}_{{{r}_{{\rm De}}}={{r}_{{\rm De}k}}}}, {\kern 185pt}\\ k=0, 1, \cdots, M-1 \\[8pt] {{\left. \dfrac{\partial {{\psi }_{{\rm Df}k}}}{\partial {{r}_{{\rm D}}}} \right|}_{{{r}_{{\rm De}}}={{r}_{{\rm De}k}}}}=\dfrac{{{K}_{{\rm f}\left( k+1 \right)}}}{{{K}_{{\rm f}k}}}{{\left. \dfrac{\partial {{\psi }_{{\rm Df}\left( k+1 \right)}}}{\partial {{r}_{{\rm De}}}} \right|}_{{{r}_{{\rm De}}}={{r}_{{\rm De}k}}}}, {\kern 140pt} \\ k=0, 1, \cdots, M-1 \\[8pt] {{\psi }_{{\rm Df}k}}\left( {{t}_{{\rm De}}} \right)=0, {\kern 251pt} \\ {{r}_{{\rm De}}}\to \infty; k = M \\\end{array} \right. $ | (23) |
将式(23)进行基于
| $ \left\{ \begin{array}{*{35}{l}}\dfrac{{{\rm d}^{2}}{{{\bar{\psi }}}_{{\rm Df}k}}}{{\rm d}r_{{\rm De}}^{2}}+\dfrac{1}{{{r}_{{\rm De}}}}\dfrac{{\rm d}{{{\bar{\psi }}}_{{\rm Df}k}}}{{\rm d}{{r}_{{\rm De}}}}+{{\lambda }_{k}}{{{\rm e}}^{-2S}}\left( \dfrac{{{K}_{{\rm f}k}}}{{{K}_{{\rm m}}}}{{{\bar{\psi }}}_{{\rm Dm}k}}-{{{\bar{\psi }}}_{{\rm Df}k}} \right)=\dfrac{{{\omega }_{k}}}{{{C}_{{\rm De}}}}\dfrac{{{K}_{{\rm f}0}}}{{{K}_{{\rm f}k}}}z{{{\bar{\psi }}}_{{\rm Df}k}}, {\kern 35pt} \\ {{r}_{{\rm De}\left( k-1 \right)}}\leqslant {{r}_{{\rm De}}}\leqslant {{r}_{{\rm De}k}} \\ -{{\lambda }_{k}}{{{\rm e}}^{-2S}}\left( {{{\bar{\psi }}}_{{\rm Dm}k}}-\dfrac{{{K}_{{\rm m}}}}{{{K}_{{\rm f}k}}}{{{\bar{\psi }}}_{{\rm Df}k}} \right)=\dfrac{1-{{\omega }_{k}}}{{{C}_{{\rm De}}}}\dfrac{{{K}_{{\rm f}0}}}{{{K}_{{\rm f}k}}}z{{{\bar{\psi }}}_{{\rm Dm}k}}, {\kern 108pt} \\ {{r}_{{\rm De}\left( k-1 \right)}}\leqslant {{r}_{{\rm De}}}\leqslant {{r}_{{\rm De}k}} \\ {{{\bar{\psi }}}_{{\rm Df}k}}({{r}_{{\rm De}}}, 0)={{{\bar{\psi }}}_{{\rm Dm}k}}({{r}_{{\rm De}}}, 0)=0, {\kern 173pt}\\ k=0, 1, \cdots, M \\ z{{{\bar{\psi }}}_{{\rm wD}}}-{{\left. \left( {{r}_{{\rm De}}}\dfrac{d{{{\bar{\psi }}}_{{\rm Df}0}}}{d{{r}_{{\rm De}}}} \right) \right|}_{{{r}_{{\rm De}}}=1}}=\dfrac{1}{z}, {\kern 180pt} \\ {{{\bar{\psi }}}_{{\rm wD}}}={{\left. {{{\bar{\psi }}}_{{\rm Df0}}} \right|}_{{{r}_{{\rm De}}}=1}} \\ {{\left. {{{\bar{\psi }}}_{{\rm Df}k}} \right|}_{{{r}_{{\rm De}}}={{r}_{{\rm De}k}}}}={{\left. {{{\bar{\psi }}}_{{\rm Df}\left( k+1 \right)}} \right|}_{{{r}_{{\rm De}}}={{r}_{{\rm De}k}}}}, {\kern 180pt} \\ k=0, 1, \cdots, M-1 \\[8pt] {{\left. \dfrac{{\rm d}{{{\bar{\psi }}}_{{\rm Df}k}}}{{\rm d}{{r}_{{\rm De}}}} \right|}_{{{r}_{{\rm De}}}={{r}_{{\rm De}k}}}}=\dfrac{{{K}_{{\rm f}\left( k+1 \right)}}}{{{K}_{{\rm f}k}}}{{\left. \dfrac{{\rm d}{{{\bar{\psi }}}_{{\rm Df}\left( k+1 \right)}}}{{\rm d}{{r}_{{\rm De}}}} \right|}_{{{r}_{{\rm De}}}={{r}_{{\rm De}k}}}}, {\kern 135pt} \\ k=0, 1, \cdots, M-1 \\[8pt] {{{\bar{\psi }}}_{{\rm Df}k}}\left( z \right)=0, {\kern 254pt} \\ {{r}_{{\rm De}}}\to \infty ; k = M \\ \end{array} \right. $ | (24) |
式中:
式(24)中,
| $ {{\bar{\psi }}_{{\rm Df}k}}={{A}_{k}}{{I}_{0}}\left( {{r}_{{\rm De}k}}\sqrt{{{S}_{k}}\left( z \right)} \right)+{{B}_{k}}{{K}_{0}}\left( {{r}_{{\rm De}k}}\sqrt{{{S}_{k}}\left( z \right)} \right), \quad k=0, 1, \cdots, M $ | (25) |
式中:
对式(25)求导,有
| $ \dfrac{{\rm d}{{{\bar{\psi }}}_{{\rm Df}k}}}{{\rm d}{{r}_{{\rm De}}}}=\sqrt{{{S}_{k}}\left( z \right)}{{A}_{k}}{{I}_{1}}\left( {{r}_{{\rm De}k}}\sqrt{{{S}_{k}}\left( z \right)} \right)-\sqrt{{{S}_{k}}\left( z \right)}{{B}_{k}}{{K}_{1}}\left( {{r}_{{\rm De}k}}\sqrt{{{S}_{k}}\left( z \right)} \right),\\ \quad k=0, 1, \cdots, M $ | (26) |
将式(26)、(25)代入式(24),求取
| $ \left\{ {\begin{array}{*{20}{l}} {z{{\bar \psi }_{{\rm{wfD}}}} - \sqrt {{S_0}\left( z \right)} {A_0}{I_1}\left( {\sqrt {{S_0}\left( z \right)} } \right) + \sqrt {{S_0}\left( z \right)} {B_0}{K_1}\left( {\sqrt {{S_0}\left( z \right)} } \right) = \dfrac{1}{z}} \\ {{{\bar \psi }_{{\rm{wfD}}}} = {A_0}{I_0}\left( {\sqrt {{S_0}\left( z \right)} } \right) + {B_0}{K_0}\left( {\sqrt {{S_0}\left( z \right)} } \right)}&{}&{}\\ {A_k}{I_0}\left( {{r_{{\rm{De}}k}}\sqrt {{S_k}\left( z \right)} } \right) + {B_k}{K_0}\left( {{r_{{\rm{De}}k}}\sqrt {{S_k}\left( z \right)} } \right) = {A_{k + 1}}{I_0}\left( {{r_{{\rm{De}}k}}\sqrt {{S_{k + 1}}\left( z \right)} } \right) + \\{\kern 20pt}{B_{k + 1}}{K_0}\left( {{r_{{\rm{De}}k}}\sqrt {{S_{k + 1}}\left( z \right)} } \right), \\ {k = 1, 2, \cdots, M - 1}\\ {A_k}\sqrt {{S_k}\left( z \right)} {I_1}\left( {{r_{{\rm{De}}k}}\sqrt {{S_k}\left( z \right)} } \right) - {B_k}\sqrt {{S_k}\left( z \right)} {K_1}\left( {{r_{{\rm{De}}k}}\sqrt {{S_k}\left( z \right)} } \right) = \\ \dfrac{{{k_{{\rm{f}}\left( {k + 1} \right)}}}}{{{k_{{\rm{f}}k}}}} {A_{k + 1}}\cdot \\{\kern 20pt}\sqrt {{S_k}\left( z \right)} {I_1}\left( {{r_{{\rm{De}}k}}\sqrt {{S_k}\left( z \right)} } \right) - \dfrac{{{K_{{\rm{f}}\left( {k + 1} \right)}}}}{{{K_{{\rm{f}}k}}}}{B_{k + 1}}\sqrt {{S_k}\left( z \right)} {K_1}\left( {{r_{{\rm{De}}k}}\sqrt {{S_k}\left( z \right)} } \right), \\ {k = 1, 2, \cdots, M - 1}\\ {{A_M} = 0} \end{array}} \right. $ | (27) |
式中:
式(27)中,参数无因次有效界面半径
由式(3)和式(17),得到无因次界面有效半径的表达式
| $ {{r}_{{\rm De}k}}=\dfrac{{{l}_{0}}}{{{r}_{{\rm w}}}}\left[1+\dfrac{\alpha \left( 1-{{\alpha }^{k}} \right)\cos \theta }{1-\alpha } \right]{{{\rm e}}^{S}} $ | (28) |
由式(6),渗透率比的表达式为
| $ \dfrac{{{K}_{{\rm f}\left( k+1 \right)}}}{{{K}_{{\rm f}k}}}=\left\{ \begin{array}{*{35}{l}}n{{\beta }^{2}}\cos \theta, {\kern 20pt}k=0 \\n{{\beta }^{2}}, {\kern 43pt} k>0 \end{array} \right. $ | (29) |
| $ {{S}_{k}}\left( z \right)=\dfrac{\dfrac{{{K}_{{\rm f}0}}}{{{K}_{{\rm f}k}}}{{\lambda }_{k}}\left( 1-{{\omega }_{k}} \right)z}{\dfrac{{{K}_{{\rm f}0}}}{{{K}_{{\rm f}k}}}\left( 1-{{\omega }_{k}} \right){{{\rm e}}^{2S}}z+{{\lambda }_{k}}{{C}_{{\rm De}}}}+ \\ {\kern 40pt}\dfrac{{{K}_{{\rm f}0}}}{{{K}_{{\rm f}k}}}\dfrac{{{\omega }_{k}}}{{{C}_{{\rm De}}}}z $ | (30) |
其中
| $ \dfrac{{{K}_{{\rm f}0}}}{{{K}_{{\rm f}k}}}={{\left( n{{\beta }^{2}} \right)}^{-k}} $ | (31) |
| $ {{\lambda }_{k}}=\left\{ \begin{array}{*{35}{l}}\dfrac{32a{{K}_{{\rm m}}}r_{{\rm w}}^{2}}{Nd_{0}^{2}},&{\quad}k=0 \\ \dfrac{32a{{K}_{{\rm m}}}r_{{\rm w}}^{2}}{N{{n}^{k}}{{\beta }^{2k}}d_{0}^{2}\cos \theta },& {\quad}k>0 \\ \end{array} \right. $ | (32) |
对式(27)进行求解,可得到拉氏空间内无因次井底拟压力
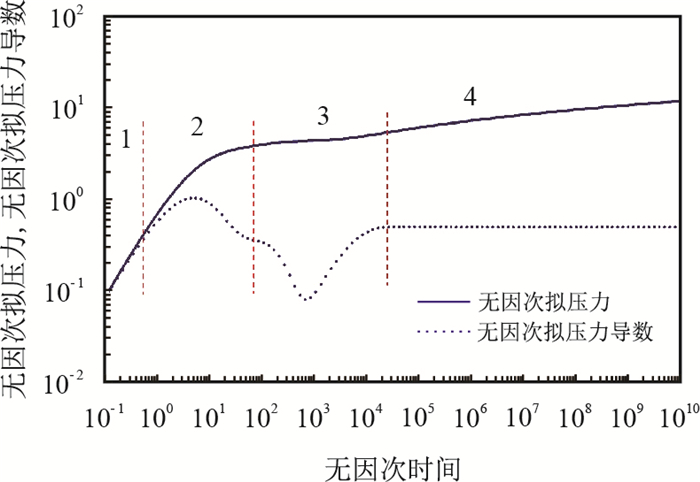 |
| 图2 基于树状分形网络的裂缝性气藏的典型曲线 Fig. 2 Typical curve of fractured gas reservoir based on tree fractal network |
树状分形网络裂缝性气藏中,各区域裂缝系统渗透率、裂缝体积相等的树状分形裂缝性气藏典型曲线,即满足式(13)。裂缝系统分形网络的参数取值为
图 3为长度比
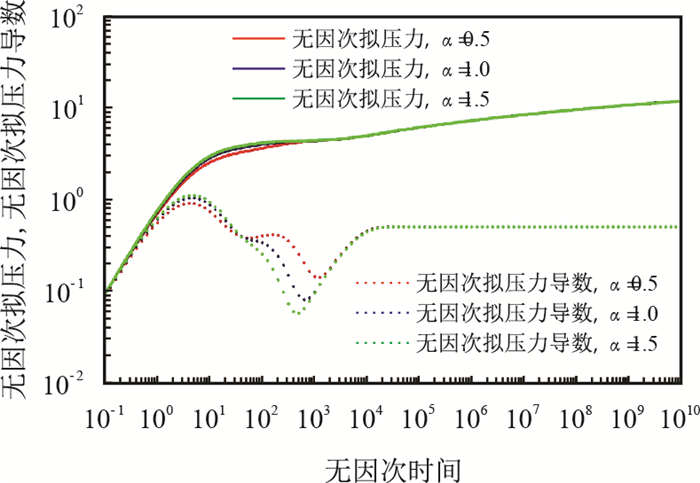 |
|
图3
长度比 |
由图 3可见,长度比
图 4为直径比
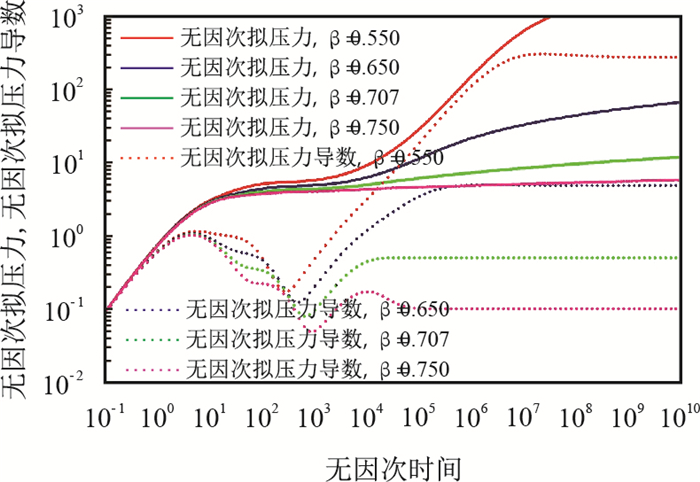 |
|
图4
直径比 |
由图 4可见,
图 5为分叉角度
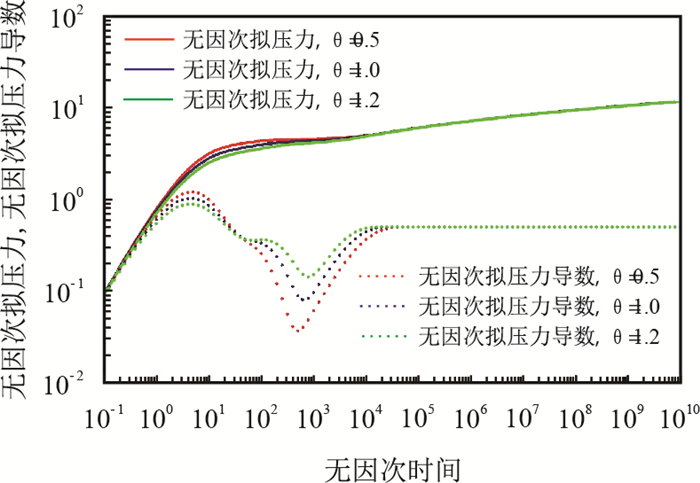 |
|
图5
分叉角度 |
由图 5可见,分叉角度
图 6、图 7分别为
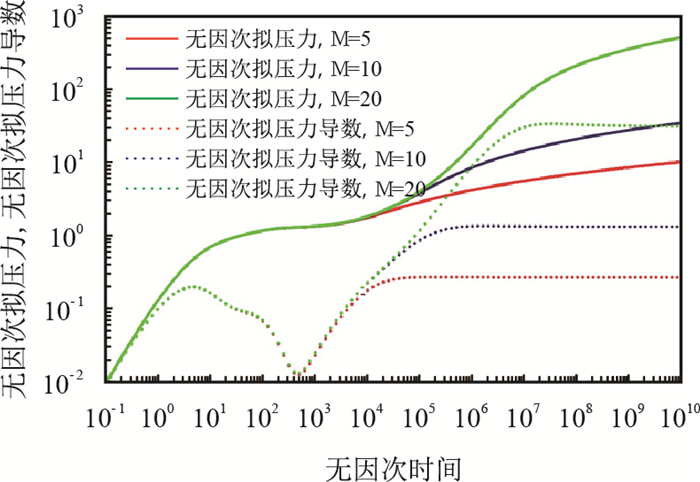 |
|
图6
总分叉级数 |
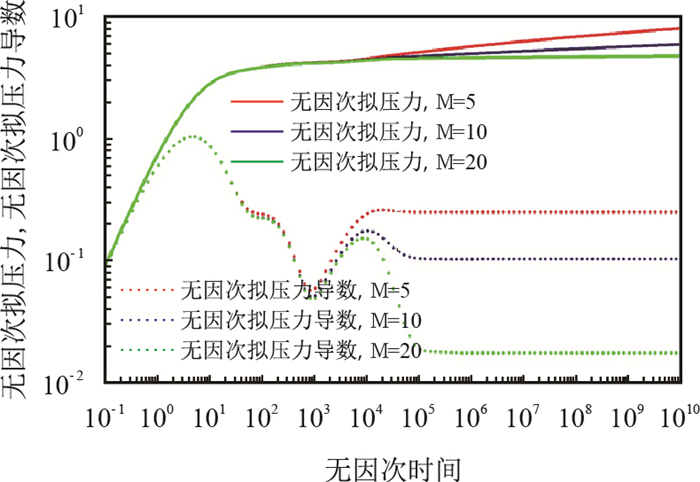 |
|
图7
总分叉级数 |
由图 6、图 7可见,总分叉级数
图 8为初始裂缝数
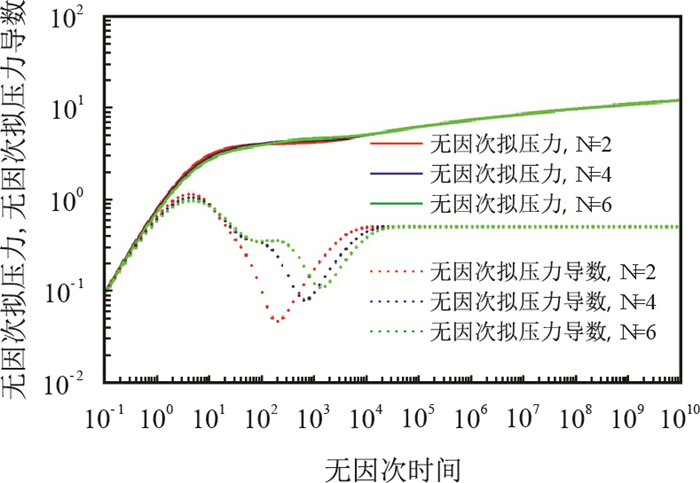 |
|
图8
初始裂缝数 |
由图 8可见,初始裂缝数
利用树状分形网络模拟裂缝系统,并将树状分形网络嵌入到基质中,提出了基于树状分形网络的裂缝性气藏试井模型,作出了树状分形网络的裂缝性气藏拟压力动态特征典型曲线。分析了长度比
| [1] |
洛纳根, 乔利. 裂缝性油气藏[M]. 北京: 石油工业出版社, 2015.
|
| [2] |
李苗, 张涛, 艾合买提江·阿布都热合曼. 裂缝型碳酸盐岩油藏试井解释中特殊现象分析[J]. 断块油气田, 2016, 23(1): 65-68. LI Miao, ZHANG Tao, AHMATJAN Abudurahman. Special phenomena in well test interpretation for fractured carbonate reservoirs[J]. Fault-Block Oil & Gas Field, 2016, 23(1): 65-68. doi: 10.6056/dkyqt201601014 |
| [3] |
姜永, 张雷, 别旭伟, 等. 裂缝性油藏注水井压降试井解释方法及应用[J]. 断块油气田, 2017, 24(4): 565-569. JIANG Yong, ZHANG Lei, BIE Xuwei, et al. Interpretation method and application for pressure fall-off test of water injection well in fractured reservoir[J]. Fault-Block Oil & Gas Field, 2017, 24(4): 565-569. doi: 10.6056/dkyqt201704028 |
| [4] |
姚军, 刘丕养, 吴明录. 裂缝性油气藏压裂水平井试井分析[J]. 中国石油大学学报(自然科学版), 2013, 37(5): 107-113. YAO Jun, LIU Piyang, WU Minglu. Well test analysis of fractured horizontal well in fractured reservoir[J]. Journal of China University of Petroleum(Edition of Natural Science), 2013, 37(5): 107-113. doi: 10.3969/j.issn.16735005.2013.05.016 |
| [5] |
魏明强, 段永刚, 李彦波, 等. 存在大尺度天然裂缝的气藏数值试井分析方法[J]. 天然气地球科学, 2014, 25(5): 778-782. WEI Mingqiang, DUAN Yonggang, LI Yanbo, et al. Study on numerical well test method of gas reservoirs with largescale fractures[J]. Natural Gas Geoscience, 2014, 25(5): 778-782. doi: 10.11764/j.issn.1672-1926.2014.05.0778 |
| [6] |
王新海, 张冬丽, 李江龙. 含有大尺度裂缝、溶洞的缝洞型油藏的数值试井模型[J]. 石油天然气学报, 2009, 31(6): 129-135. WANG Xinhai, ZHANG Dongli, LI Jianglong. A numerical well testing model for a fractured and vuggy reservoirs containing big fractures and vugs[J]. Journal of Oil and Gas Technology, 2009, 31(6): 129-135. doi: 10.3969/j.issn.1000-9752.2009.06.025 |
| [7] |
李林地, 谭学群, 庚勐. 数值试井技术在裂缝性碳酸盐岩油藏中的应用[J]. 油气井测试, 2013, 22(2): 22-24. LI Lindi, TAN Xuequn, GENG Meng. Application of numerical well test analysis in fractured carbonate reservoir[J]. Well Testing, 2013, 22(2): 22-24. doi: 10.3969/j.issn.1004-4388.2013.02.008 |
| [8] |
李顺初, 张建军. 分形双孔介质油藏试井分析解的相似结构[J]. 钻采工艺, 2006, 25(4): 28-30. LI Shunchu, ZHANG Jianjun. Similar structure of pressure distribution in the fractal dual porosity rese[J]. Drilling & Production Technology, 2006, 25(4): 28-30. doi: 10.3969/j.issn.1673-159X.2006.01.013 |
| [9] |
李顺初. 分形双孔介质封闭油气藏的试井模型[J]. 新疆石油地质, 2003, 24(2): 149-154. LI Shunchu. Well test model for fractal dual porosity closed reservoir[J]. Xinjiang Petroleum Geology, 2003, 24(2): 149-151. doi: 10.3969/j.issn.1001-3873.2003.02.019 |
| [10] |
ZHANG Yigen, TONG Dengke. The pressure transient analysis of deformation of fractal medium[J]. Journal of Hydrodynamics Ser B, 2008, 20(3): 306-313. doi: 10.1016/S1001-6058(08)60062-1 |
| [11] |
ZHANG Liehui, ZHANG Jinliang, ZHAO Yulong. Analysis of a finite element numerical solution for a nonlinear seepage flow model in a deformable dual media fractal reservoir[J]. Journal of Petroleum Science & Engineering, 2011, 76(3): 77-84. doi: 10.1016/j.petrol.2010.11.024 |
| [12] |
FLAMENCO-LOPEZ F, CAMACHO-VELAZQUEZ R. Determination of fractal parameters of fracture networks using pressure-transient data[J]. SPE Reservoir Evaluation & Engineering, 2003, 6(1): 39-47. doi: 10.2118/82607-PA |
| [13] |
ACUNA J A, Yortsos Y C. Practical application of fractal pressure-transient analysis in naturally fractured reservoirs[J]. SPE Formation Evaluation, 1995, 10(3): 173-179. doi: 10.2118/24705-PA |
| [14] |
YANG Shanshan, FU Huahua, YU Boming. Fractal analysis of flow resistance in tree-like branching networks with roughened microchannels[J]. Fractals, 2017, 25(1): 1750008-1-1750008-8. doi: 10.1142/S0218348X17500086 |
| [15] |
XU P, SASMITO A P, YU B, et al. Transport phenomena and properties in treelike networks[J]. Applied Mechanics Reviews, 2016, 68(4): 040802-040802-17. doi: 10.1115/1.4033966 |
| [16] |
WECHSATOL W, LORENTE S, BEJAN A. Tree-shaped insulated designs for the uniform distribution of hot water over an area[J]. International Journal of Heat & Mass Transfer, 2001, 44(16): 3111-3123. doi: 10.1016/S00179310(00)00338-0 |
| [17] |
LORENTE S, WECHSATOL W, BEJAN A. Tree-shaped flow structures designed by minimizing path lengths[J]. International Journal of Heat & Mass Transfer, 2002, 45(16): 3299-3312. doi: 10.1016/S0017-9310(02)00051-0 |
| [18] |
WECHSATOL W, LORENTE S, BEJAN A. Optimal treeshaped networks for fluid flow in a disc-shaped body[J]. International Journal of Heat & Mass Transfer, 2002, 45(25): 4911-4924. doi: 10.1016/S0017-9310(02)00211-9 |
| [19] |
XU Peng, YU Boming, QIU Shuxia, et al. An analysis of the radial flow in the heterogeneous porous media based on fractal and constructal tree networks[J]. Physica A Statistical Mechanics & Its Applications, 2008, 387(26): 6471-6483. doi: 10.1016/j.physa.2008.08.021 |
| [20] |
WARREN J E. The behavior of naturally fractured reservoirs[J]. Soc of Petroleum Engineers Journal, 1963, 3(3): 245-255. doi: 10.2118/426-PA |
| [21] |
VELAZQUEZ R C, FUENTES-CRUZ G, VASQUEZCRUZ M A. Decline curve analysis of fractured reservoirs with fractal geometry[J]. SPE Reservoir Evaluation & Engineering, 2008, 11(3): 606-619. doi: 10.2118/104009-MS |
 2018, Vol. 40
2018, Vol. 40


