近年来,油田套管腐蚀越来越严重,据统计,大港油田某区块套管腐蚀达到34.4%,其腐蚀情况如图 1所示。研究发现,该区块腐蚀主要由CO
 |
|
图1
官X井套管腐蚀图
Fig. 1
The casing |
针对油田套管腐蚀问题,许多专家学者对此进行了大量研究。1990年,Coulson等对套管轴向双腐蚀缺陷进行了研究,探讨了双点腐蚀缺陷的相互作用机理,得出腐蚀缺陷的相互作用与腐蚀缺陷的长度、宽度、深度等参数密切相关,并且提出了相互作用准则[1]。油田套管腐蚀大多是成片腐蚀,即在一定的范围,存在多个腐蚀坑,多腐蚀坑的相互作用机理的研究对油田腐蚀情况的研究和评价有实际意义。1992年,O
为了更深入和更准确地评价具有腐蚀坑的套管强度,基于弹性力学理论和具有球形腐蚀坑的套管力学模型,建立了具有两个腐蚀坑缺陷的套管-水泥环-地层三维有限元模型,研究了相邻腐蚀坑的套管上的应力分布规律及套管上的应力随腐蚀坑距离、腐蚀坑深的变化情况,基于双腐蚀坑的套管应力分布情况的基础,建立了具有单个腐蚀坑缺陷的套管-水泥环-地层三维有限元模型,研究了腐蚀坑的半径,腐蚀坑的深度对套管强度的影响。
1 有腐蚀坑缺陷的套管强度评估模型 1.1 套管的力学模型假设套管受均匀外压,根据弹性力学的厚壁圆筒理论,厚壁圆筒平面受力图见图 2,其内半径为
| $ \left\{ \begin{array}{l} {{\sigma }_{r}}=\dfrac{r_{1}^{2}}{r_{2}^{2}-r_{1}^{2}}\left( 1-\dfrac{r_{2}^{2}}{{{r}^{2}}} \right){{p}_{\rm i}}-\dfrac{r_{2}^{2}}{r_{2}^{2}-r_{1}^{2}}\left( 1-\dfrac{r_{1}^{2}}{{{r}^{2}}} \right){{p}_{\rm o}} \\ {{\sigma }_{\theta }}=\dfrac{r_{1}^{2}}{r_{2}^{2}-r_{1}^{2}}\left( 1+\dfrac{r_{2}^{2}}{{{r}^{2}}} \right){{p}_{\rm i}}-\dfrac{r_{2}^{2}}{r_{2}^{2}-r_{1}^{2}}\left( 1+\dfrac{r_{1}^{2}}{{{r}^{2}}} \right){{p}_{\rm o}} \\ \end{array} \right. $ | (1) |
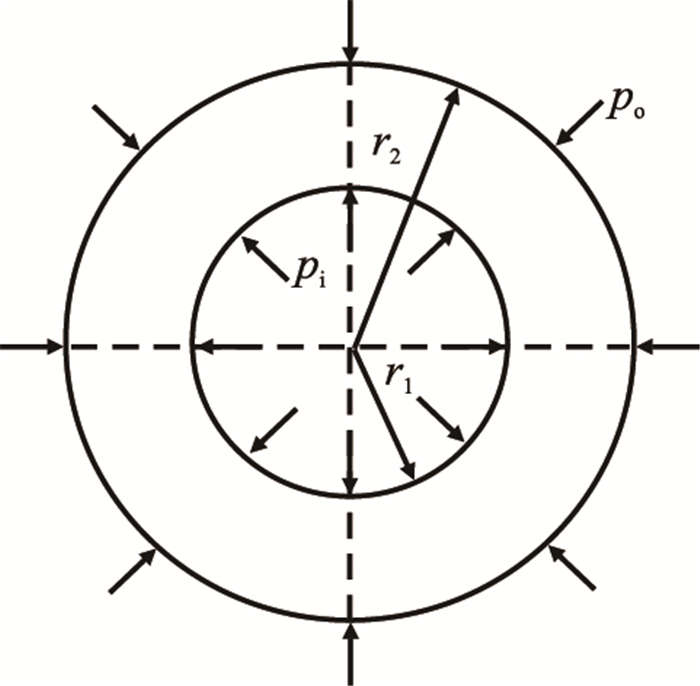 |
| 图2 厚壁圆筒力学模型 Fig. 2 The mechanical model of heavy wall cylinder |
式中:
根据拉梅公式,可以得到套管,水泥环,地层的应力分布情况。
1.2 有腐蚀坑缺陷的套管模型简化及力学模型现场调研发现,CO2腐蚀坑大多呈浅球形(图 1中腐蚀部位),其他介质造成的腐蚀坑形状较为复杂,为方便研究,将腐蚀坑简化为规则的浅球形来模拟,图 3是通过现场腐蚀坑简化后的具有腐蚀坑缺陷的套管部分图,腐蚀坑为浅球形。
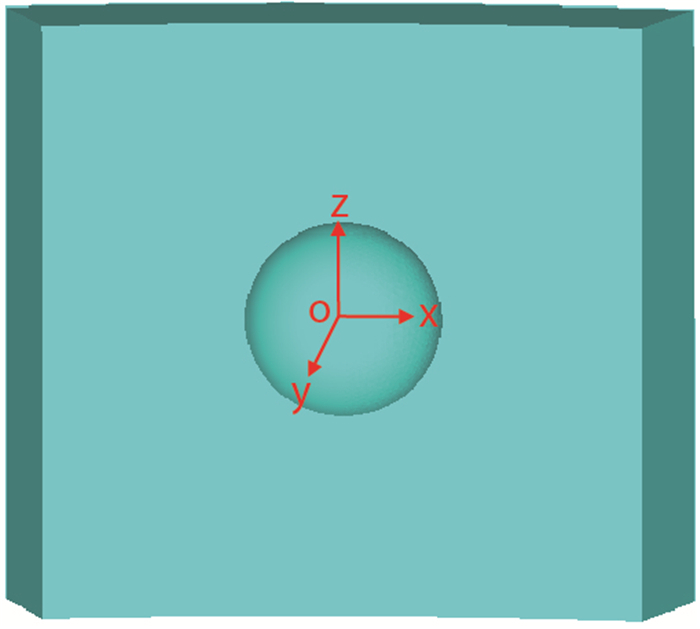 |
|
图3
套管内腐蚀坑简化模型图
Fig. 3
The map of casing |
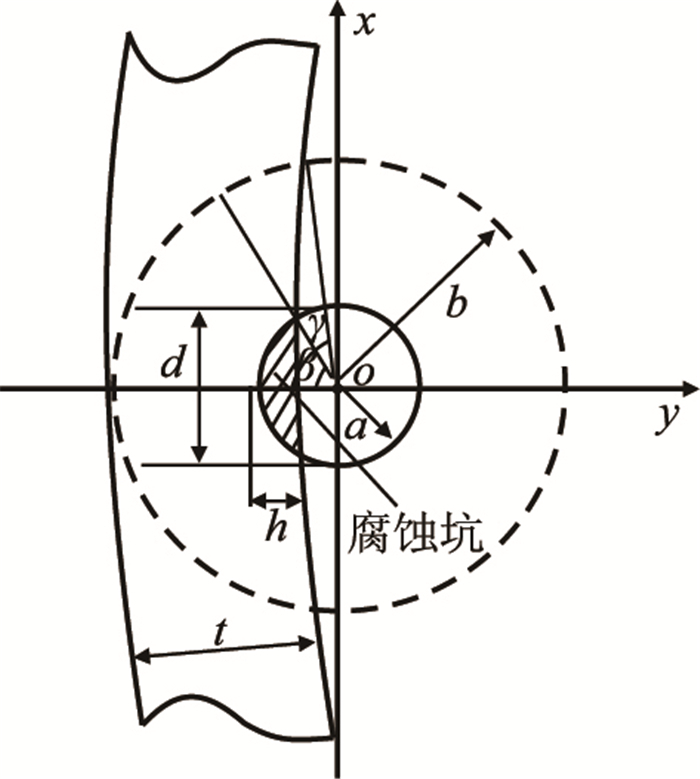
图 4是图 3沿
| $ \sigma ={{\sigma }_{0}}\left[1+\dfrac{4-5\mu }{2\left( 7-5\mu \right)}\dfrac{{{a}^{3}}}{{{r}^{3}}}+\dfrac{9}{2\left( 7-5\mu \right)}\dfrac{{{a}^{5}}}{{{r}^{5}}} \right] $ | (2) |
 |
|
图4
腐蚀坑平面模型图
Fig. 4
The 2D model of casing |
式中:
当
| $ \sigma =\dfrac{27-15\mu }{2\left( 7-5\mu \right)}{{\sigma }_{0}} $ | (3) |
假设腐蚀坑为球的一部分(图 4),其应力集中系数
| $ {{K}_{{\rm tg}}}=\dfrac{{{b}^{2}}\gamma -\left( a-h \right)\sqrt{{{b}^{2}}-{{\left( a-h \right)}^{2}}}}{{{b}^{2}}\gamma -{{a}^{2}}\beta -{{\left( a-h \right)}^{2}}\left( \tan\gamma -\tan\beta \right)+\dfrac{{{a}^{3}}\left( 4m-5m\mu +3{{a}^{2}}n \right)}{\left( 7-5\mu \right)}}\dfrac{27-15\mu }{14-10\mu } $ | (4) |
式中:
根据现场调研,套管上发生的局部腐蚀,除了单点腐蚀缺陷以外还会以相邻双点腐蚀或者多点腐蚀的形式存在。而相邻腐蚀缺陷之间的距离较近时应力可能会发生相互作用,所以近距离相邻腐蚀则不能简单按照单腐蚀缺陷的情况来评价套管的腐蚀,图 5为相邻腐蚀坑位置关系图(
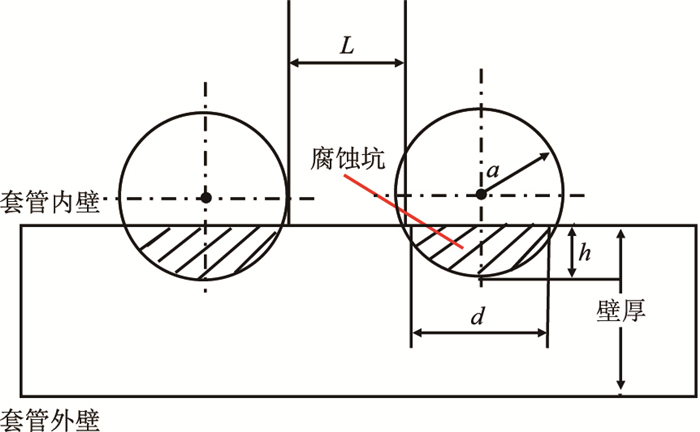 |
|
图5
相邻腐蚀坑位置关系
Fig. 5
The relationship of casing |
建立具有两个腐蚀坑缺陷的套管-水泥环-地层三维有限元模型,模型研究地层半径1 000 mm,取部分井筒,长度3 000 mm,建立1/2模型进行研究,腐蚀缺陷建立在模型中部,其力学模型及具有腐蚀坑缺陷套管局部放大图见图 6和图 7所示,图中,
 |
| 图6 有限元实体模型 Fig. 6 Finite-element physical model |
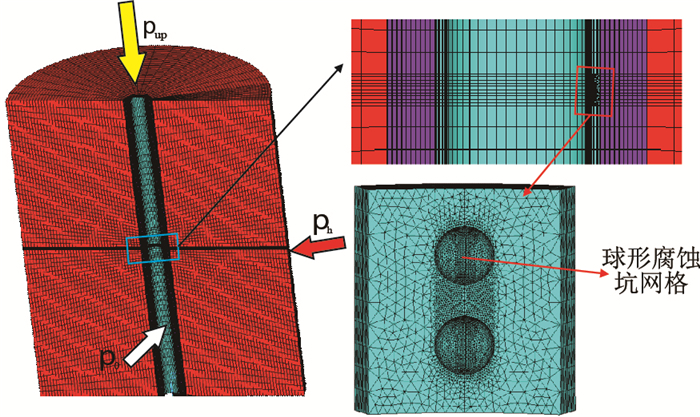 |
| 图7 有限元力学模型 Fig. 7 Finite-element mechanics model |
根据本研究建立的有两个腐蚀坑缺陷的套管-水泥环-地层三维有限元模型(图 6,图 7),根据现场调研,用不同相邻腐蚀坑距离和腐蚀坑深度,在一定的地层条件下,用有限元分析软ANSYS进行数值模拟分析。
图 8是腐蚀坑半径为5.0 mm,腐蚀坑深度为4.5 mm时,用外径为139.7 mm,壁厚为9.17 mm的P110钢级套管模拟的相邻腐蚀坑不同距离的应力云图(
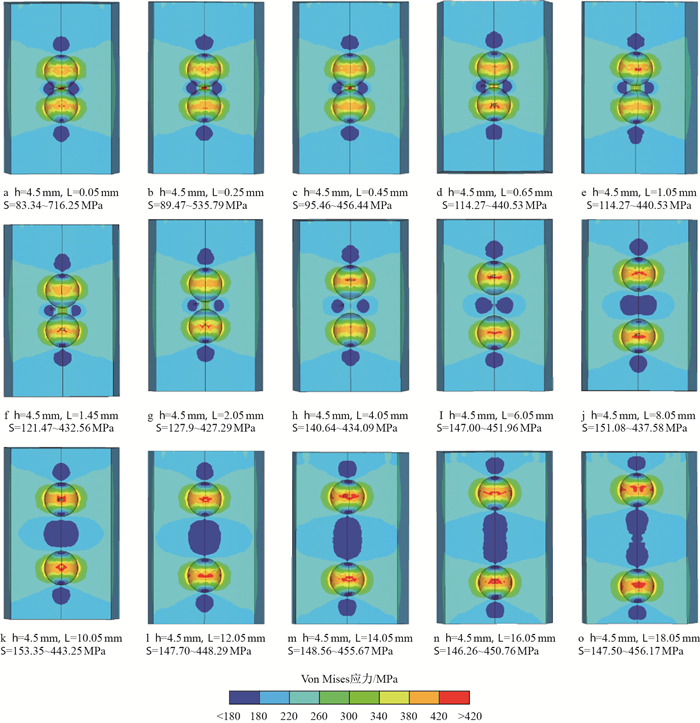 |
| 图8 相邻腐蚀坑不同距离的应力云图 Fig. 8 The Von Mises stress contours of adjacent corrosion pits in different distance |
由图 8可知,当腐蚀坑距离
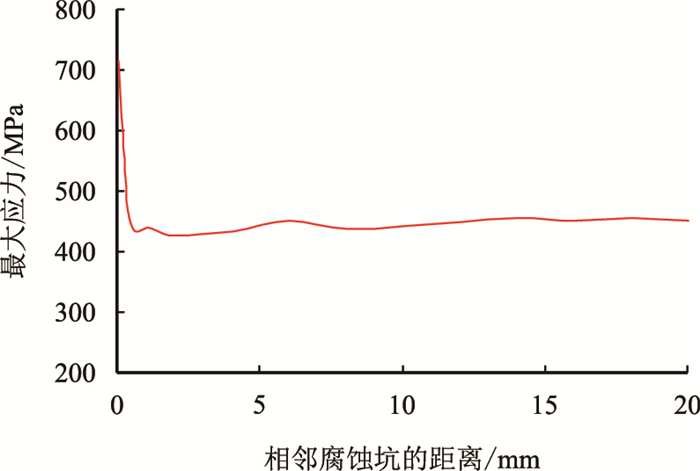 |
| 图9 套管最大应力与相邻腐蚀坑距离的关系 Fig. 9 The relationship maximum stress of casing with distance of adjacent corrosion pits |
由图 9可知,腐蚀坑半径和深度一定时,在两腐蚀坑的距离大于0.65 mm后,套管上的最大应力基本不变,也就是两个腐蚀坑的相互影响较小。而在实际油田中,腐蚀坑之间的距离多在1.00 mm以上,因此可以用单个腐蚀坑模型来评价套管的强度。
2.3 单个腐蚀坑缺陷的套管有限元计算结果分析根据相邻腐蚀坑的分析,可以用单个腐蚀坑缺陷模型来评价现场套管的强度。因此建立单个腐蚀坑缺陷的套管-水泥环-地层三维有限元模型对腐蚀套管进行强度评估,其结果如下。
2.3.1 有腐蚀坑缺陷的套管应力分布情况图 10为地层弹性模量为24.48 GPa,采用外径为139.70 mm,壁厚为9.17 mm的P110套管,腐蚀坑半径为7.0 mm,腐蚀坑深度为6.5 mm时地层、水泥环、套管内Mises应力云图。
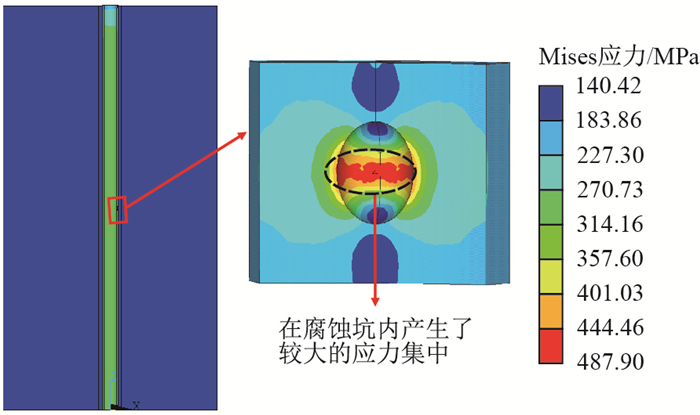 |
| 图10 单个腐蚀坑的地层-水泥环-套管内Mises应力云图 Fig. 10 The Von Mises stress contours of casing-cement-formation with a corrosion pit |
由图 10中的局部放大图可知,最大应力发生在腐蚀坑内,最大应力为487.90 MPa,在腐蚀坑内产生了较大的应力集中。用ANSYS的Query Results得到距离腐蚀坑较远处的套管的应力,即没有腐蚀坑影响的应力为221.24 MPa,经计算,其应力集中系数达到2.21,严重降低了套管的强度。并且在距离腐蚀坑一定的范围,套管上的应力相差不大,即腐蚀坑应力集中在腐蚀坑周围较小的范围。
2.3.2 腐蚀坑深、半径对套管受力、应力集中的影响图 11是腐蚀深度为0.5
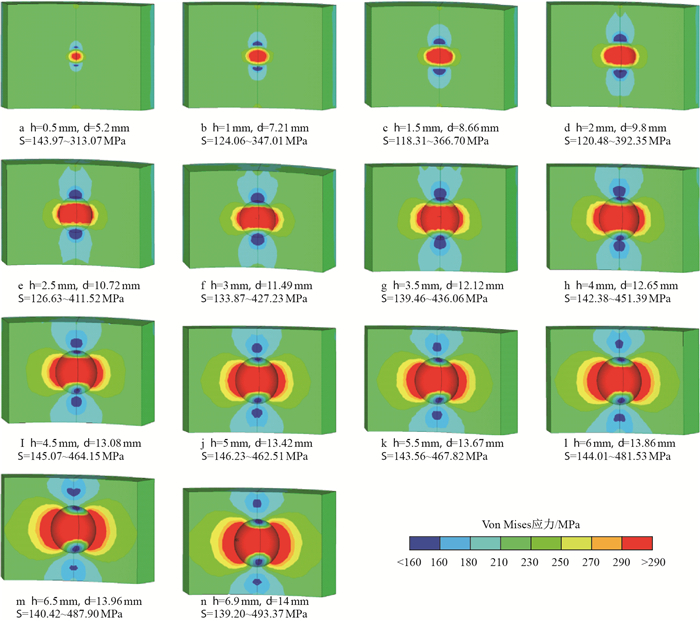 |
| 图11 套管内的Von Mises应力分布与腐蚀坑坑深的变化关系 Fig. 11 The Von Mises stress contours of casing-cement-formation with a corrosion pit different depth of corrosion pit |
腐蚀坑的最大应力随不同的半径、腐蚀坑深度变化规律如图 12所示。
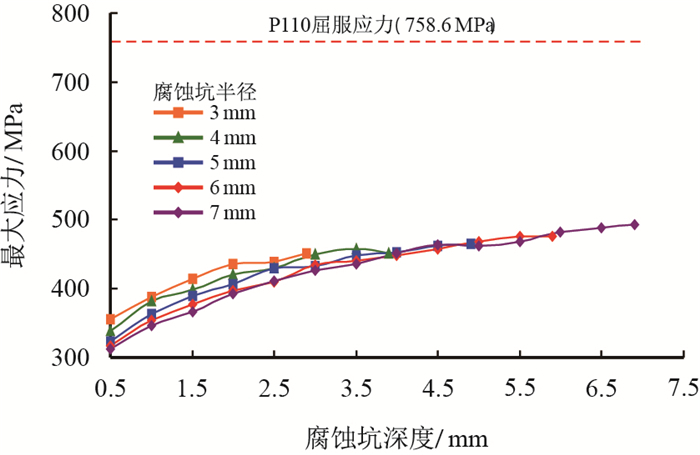 |
| 图12 腐蚀坑内最大应力随其半径、深度的变化 Fig. 12 The maximum stress curves of casing with different radius and depth of corrosion pit |
由图 12可知,当腐蚀坑半径一定时,套管的最大应力随腐蚀坑深度的增加而增大;当腐蚀坑深度相同时,腐蚀坑半径越小,腐蚀坑内的最大应力越大,即应力集中程度越大。
图 13为套管的应力集中系数随其半径、深度的变化关系图。
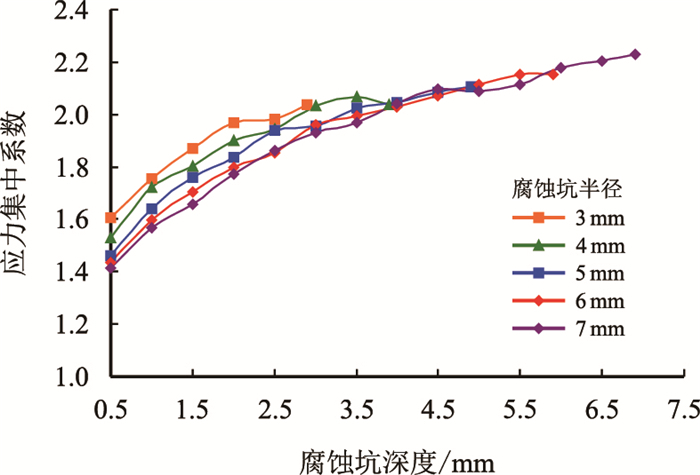 |
| 图13 腐蚀坑内应力集中系数随其半径、深度的变化 Fig. 13 The stress concentration factor of casing with different radius and depth of corrosion pit |
由图 13可知,当腐蚀坑半径一定时,腐蚀坑内的应力集中系数随着腐蚀坑的深度增加而增大,而腐蚀坑半径越小,应力集中系数越大,并且应力集中系数均在1.4以上,最大应力集中系数达到2.0以上,因此在有点腐处,即使腐蚀不穿孔,应力集中也可能使套管发生塑性破坏。
图 14为单腐蚀和腐蚀坑距离为5.0 mm时的双腐蚀坑套管内的最大应力曲线(其他条件与图 10相同)。
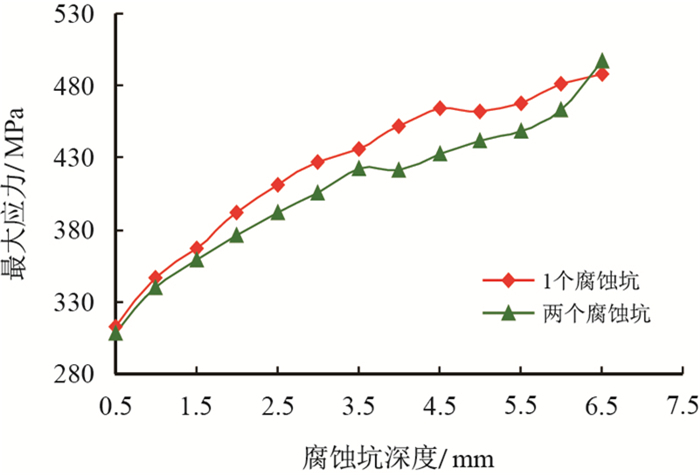 |
|
图14
单双腐蚀坑缺陷套管最大应力随深度的变化关系
Fig. 14
The casing |
由图 14可知,两个腐蚀坑时,在没有腐蚀坑相互作用时,套管的最大应力略小于相同情况下单腐蚀坑时的套管最大应力。
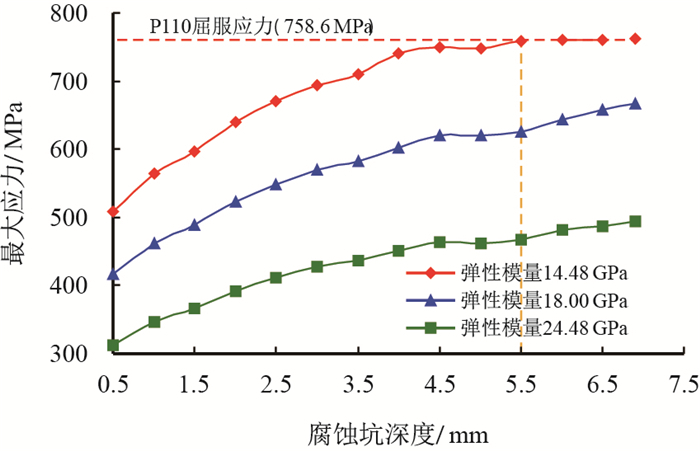
2.3.3 有腐蚀坑缺陷的套管在地层水化后对套管受力及应力集中系数的影响当地层水化后,其弹性模量会降低,水化程度越高,弹性模量降低程度越大。图 15是地层弹性模量分别为14.48,18.00和24.48 GPa时,使用外径为139.7 mm,壁厚为9.17 mm的P110钢级套管,当腐蚀半径为7 mm,腐蚀深度为0.5
 |
|
图15
套管内最大Mises应力随其坑深、地层弹性模量的变化图
Fig. 15
The maximum stress curves of casing with different depth of corrosion pit and Young |
由图 15可知,当腐蚀坑深度相同时,套管的最大应力随着地层水化程度的增加(弹性模量的降低)而增大,当地层弹性模量为14.48 GPa时,腐蚀坑深超过5.5 mm后,套管开始发生塑性破坏,而地层弹性模量为18.00,24.48 GPa地层的套管均处于安全工作状态,但是当腐蚀继续进行,腐蚀坑深继续增加,地层弹性模量较大的套管也将损坏。
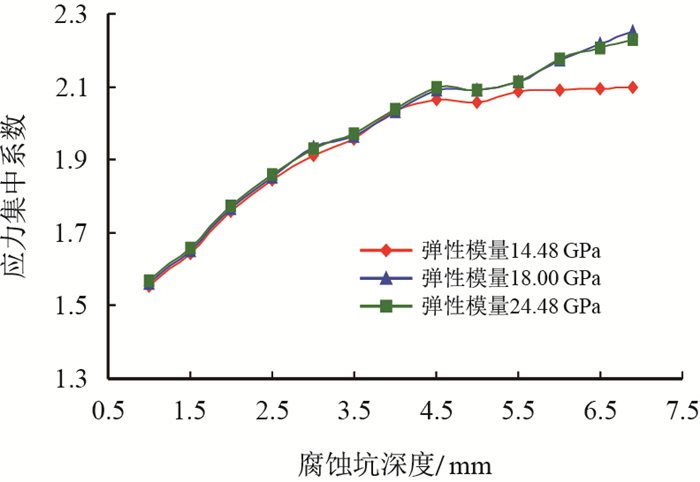
图 16为套管内应力集中系数随腐蚀坑深、地层弹性模量的变化关系图。
 |
|
图16
套管内应力集中系数随其坑深、地层弹性模量的变化关系
Fig. 16
The stress concentration factor of casing with different depth of corrosion pit and Young |
由图 16可知,不同地层弹性模量的应力集中系数差别不大,即水化程度对应力集中系数影响较小。
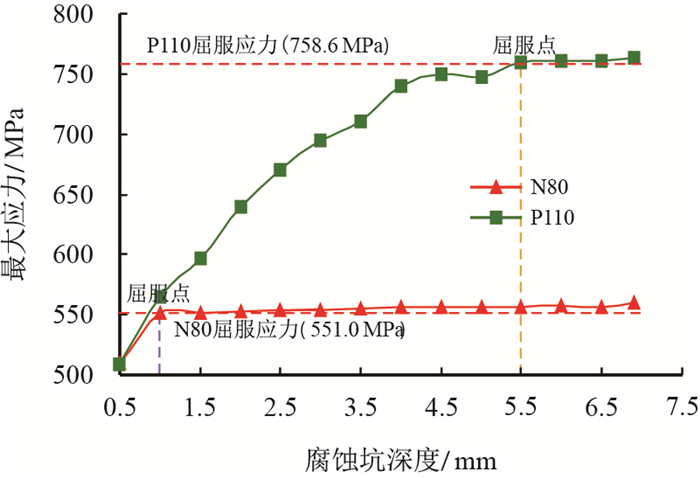
2.3.4 腐蚀坑缺陷对不同钢级的套管受力影响图 17为地层水化到一定程度时,地层弹性模量为14.48 GPa,腐蚀坑半径7.0 mm,腐蚀深度0.5
 |
|
图17
N80/P110套管最大应力与坑深的关系
Fig. 17
The N80/P110 casing |
由图 17可知,当腐蚀坑深超过1.0 mm时,N80套管开始发生屈服破坏,而P110套管在腐蚀坑深超过5.5 mm时才开始屈服破坏,因此提高钢级有助于套管的抗腐蚀能力。
由以上研究可知,在腐蚀环境中,套管被腐蚀后,在腐蚀坑周围会产生较大的应力集中,即使腐蚀不穿孔,应力集中也可能使套管发生屈服。因此,在腐蚀环境中,建议使用抗腐蚀材料的套管和防腐剂缓解套管腐蚀;其次用较高钢级的套管延长套管的适用寿命。
3 结论(1) 相邻腐蚀坑之间的距离大于0.65 mm时,当腐蚀坑半径和深度一定时,套管上的最大应力基本不变,因此可以用单个腐蚀坑模型来评价套管的强度。
(2) 有腐蚀坑缺陷的套管,其最大Mises应力随腐蚀坑深的增加而增加,在没有相邻腐蚀坑相互作用时,单腐蚀坑的最大应力略大于相同情况下相邻腐蚀坑最大应力。
(3) 套管腐蚀坑内的应力集中系数随着腐蚀坑的深度增加而增大,最大应力集中系数达到2.0以上,且腐蚀坑半径越小,应力集中系数越大。
(4) 有腐蚀坑缺陷的套管当遇到地层水化等地层条件变化时,会加快套管的损坏。
(5) 在同样的地层条件下,较高钢级套管具有更好的抗腐蚀的能力。
| [1] | COULSON K, WORTHINGAM R. New guidelines promise more accurate damage assessment[J]. Oil and Gas Journal, 1990, 88(16): 41–45. |
| [2] | O'GRADY T, HISEY D, KIEFNER J. A systematic method for the evaluation corroded pipelines[J]. Pipelines Engineering, ASME, 1992, 46: 27–35. |
| [3] |
赵新伟, 罗金恒, 路民旭. 含腐蚀缺陷管道剩余强度的有限元法分析[J].
油气储运, 2001, 20(3): 18–21.
ZHAO Xinwei, LUO Jinheng, LU Minxu. FEM analysis on the effect of corroded flaw interaction on remaining[J]. Storage of Line Yipe, 2001, 20(3): 18–21. doi: 10.3969/j.issn.1000-8241-D.2001.03.005 |
| [4] |
董事尔, 何东升, 张鹏, 等. 双点腐蚀管道的弹塑性有限元分析[J].
机械, 2005, 32(9): 20–22.
DONG Shi'er, HE Dongsheng, ZHANG Peng, et al. The elastic and plastic finite element analysis of double points corrosive pipe[J]. Machinery, 2005, 32(9): 20–22. doi: 10.-3969/j.issn.1006-0316.2005.09.008 |
| [5] | SUN K, GUO B, GHALAMBOR A. Casing strength degradation due to corrosion-applications to casing pressure assessment[J]. SPE 88009-MS, 2004. doi: 10.2118/-88009-MS |
| [6] |
李春福. 油气开发过程中的CO2腐蚀机理及防护技术研究[D]. 成都: 西南石油学院, 2005.
LI Chunfu. Study on mechanic and protection technique on CO2 corrosion research in the process of oil and gas production[D]. Chengdu: Southwest Petroleum University, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10615-2006012213.htm |
| [7] |
翟云皓, 郭兴蓬, 曲良山, 等. 集输管道腐蚀评价及剩余寿命预测[J].
油气田地面工程, 2006, 25(4): 47–48.
DI Yunhao, GUO Xingpeng, QU Liangshan, et al. The corrosion assessment and residual life prediction of gathering pipelines[J]. Oil-Gasfield Surface Engineering, 2006, 25(4): 47–48. doi: 10.3969/j.issn.1006-6896.2006.04.031 |
| [8] |
李继丰. 油井管柱抗CO2腐蚀技术研究[D]. 大庆: 大庆石油大学, 2006.
LI Jifeng. The technological research of oil well string resisting corrosion of carbon dioxide[D]. Daqing: Daqing Petroleum University, 2006. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y965104 |
| [9] | CROLET J L. Acid corrosion in wells(CO2, H2S):Metallurgical aspects[J]. SPE 10045-PA, 1983. doi: 10.2118/-10045-PA |
| [10] |
周波, 崔润炯, 刘建中. 增强型13Cr钢抗CO2腐蚀套管的研制[J].
钢管, 2006, 35(6): 22–26.
ZHOU Bo, CUI Runjiong, LIU Jianzhong. R & D of enhancement 13Cr steel anti-CO2 corrosion oil casing[J]. Steel Pipe, 2006, 35(6): 22–26. doi: 10.3969/j.issn.1001-2311.2006.06.005 |
| [11] | CAI J H, YAN J Y, YAN J, et al. Carbon dioxide corrosion of a casing steel effect of environments and temperature[C]//Canadian International Petroleum Conference, 13-15 June, Calgary, Alberta, 2006: 555-562. doi: 10.-2118/2006-194 |
| [12] | KINZEL H, KIESS C, WACHS T. New ways of handling and running C. R. A. tubulars prevent corrosion in H2S and CO2 environments[J]. Khirurgiia, 2006, 4(12): 75–76. doi: 10.2118/100181-MS |
| [13] | YAN W, DENG J, DONG X. Experimental study of 3% Cr tubing steel in CO2 and CO2/H2S corrosion environment[J]. Oil & Gas Facilities, 2012, 1(5): 43–48. doi: 10.-2118/157302-PA |
| [14] |
马颖丽. 几种110钢级套管在酸性油气田的腐蚀行为及防护措施研究[D]. 成都: 西南石油大学, 2012.
MA Yingli. Study on corrosion behavior and protection methods of several 110 grade casings in sour oil/gas fields[D]. Chengdu: Southwest Petroleum University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10615-1016030053.htm |
| [15] |
马晓勇, 翟晓鹏, 张艺馨, 等. 用数理统计方法预测油套管腐蚀剩余寿命[J].
断块油气田, 2013, 20(4): 513–515.
MA Xiaoyong, ZHAI Xiaopeng, ZHANG Yixin, et al. Using mathematical statistics method to predict remaining life of corroded tubing and casing[J]. Fault-Block Oil & Gas Field, 2013, 20(4): 513–515. doi: 10.6056/-dkyqt201304027 |
| [16] |
李波. 气井井筒的CO2腐蚀机理及剩余寿命预测[D]. 成都: 西南石油大学, 2013.
LI Bo. Study on mechanic on CO2 corrosion and residual life prediction of gas well[D]. Chengdu: Southwest Petroleum University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10615-1014159469.htm |
| [17] |
杨茜. 压力管道腐蚀缺陷的非线性有限元分析[D]. 西安: 西安石油大学, 2014.
YANG Qian. Non-linear finite element analysis for the corrosion defects of pressure pipelines[D]. Xi'an: Xi'an Shiyou University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10705-1015551499.htm |
| [18] |
王利波. 腐蚀管道剩余强度评价及剩余寿命预测软件开发[D]. 西安: 西安石油大学, 2014.
WANG Libo. The software development for residual strength assessment and residual life prediction of corroded pipelines[D]. Xi'an: Xi'an Shiyou University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10705-1015551513.htm |
| [19] |
孙磊. 三元复合驱套管腐蚀原因及临界剩余壁厚研究[D]. 大庆: 东北石油大学, 2015.
SUN Lei. A study of the reason for casing corrosion in the asp flooding and the critical residual wall thickness[D]. Daqing: Northeast Petroleum University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10220-1015362766.htm |
| [20] |
刘然克. 典型H2S/CO2环空环境下高强油套管钢应力腐蚀机理与防护[D]. 北京: 北京科技大学, 2015.
LIU Ranke. Stress corrosion cracking behavior and prevention of high strength tubing steels in typical H2S/CO2 annulus environments[D]. Beijing: University of Science and Technology Beijing, 2015. http://ir.ustb.edu.cn/handle/400002224/71883 |
| [21] | LIN T, ZHANG Q, LIAN Z, CHANG X, et al. Evaluation of casing integrity defects considering wear and corrosionapplication to casing design[J]. Journal of Natural Gas Science & Engineering, 2016, 29: 440–452. doi: 10.1016/j.-jngse.2016.01.029 |
| [22] |
林海, 许杰, 范白涛, 等. 渤海油田井下管柱CO2腐蚀规律与防腐选材现状[J].
表面技术, 2016, 45(5): 97–103.
LIN Hai, XU Jie, FAN Baitao, et al. Review on CO2 corrosion rule of down-hole strings in Bohai Oilfield and current status of anticorrosion material selection[J]. Surface Technology, 2016, 45(5): 97–103. doi: 10.16490/j.cnki.-issn.1001-3660.2016.05.015 |
| [23] |
钟功祥, 石强, 赵乾坤. 含CO2油气管道内腐蚀模拟及剩余寿命预测[J].
表面技术, 2016, 45(11): 106–112.
ZHONG Gongxiang, SHI Qiang, ZHAO Qiankun. Corrosion simulation inside oil-gas pipelines containing CO2 and prediction of residual life[J]. Surface Technology, 2016, 45(11): 106–112. doi: 10.16490/j.cnki.issn.1001-3660.2016.11.016 |
| [24] |
万力维. 酸性环境油套管设计及适用性评价[D]. 成都: 西南石油大学, 2016.
WAN Liwei. Design casing and tubing and fit for purpose in acid enviorment[D]. Chengdu: Southwest Petroleum University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10615-1016099994.htm |
| [25] |
徐芝纶.
弹性力学[M]. 北京: 高等教育出版社, 2006.
XU Zhilun. Elasticity[M]. Beijing: Higher Education Press, 2006. |
| [26] |
李志明, 殷有泉.
油水井套管外挤力计算及其力学基础[M]. 北京: 石油工业出版社, 2006.
LI Zhiming, YIN Youquan. Calculation of casing external pressure and its mechanical basis in oil-water well[M]. Beijing: Petroleum Industry Press, 2006. |
| [27] | TIMOSHENKO S P, GOODIER J N. Theory of elasticity[M]. 2nd Edition. New York: McGraw-Hill, 1951. |
 2018, Vol. 40
2018, Vol. 40


